基于考题分析的圆锥曲线内容备考探究
2016-03-25罗义铭汤强
罗义铭++汤强

摘 要: 2016年全国将有26个省(市)使用全国统一命题试卷,而且圆锥曲线是每年高考中的一个必考内容,那么全国统一命题试卷在圆锥曲线的考查有什么样的特点?针对这些特点,如何备考呢?本文主要通过对六年的全国卷高考试题圆锥曲线部分进行分析研究,以期对复习备考有些许指导意义.
关键词: 圆锥曲线 全国卷 备考
圆锥曲线是高中数学课程中解析几何部分的核心内容,是学生进一步学习几何的重要基础.由于它具有丰富的思想性(其包含了大量的数学思想方法,如:数形结合思想、转化与化归思想、分类讨论思想,函数与方程思想、函数与不等式思想、整体思想、待定系数法、坐标法等)、较强的综合性(它能很好地与其他知识(如函数、数列、向量、不等式、三角等)相结合)、计算的复杂性(运算量大)、题目的灵活性(形式多变,题源背景丰富)等特点,它能很好地考查学生的数学知识结构、运算求解能力、分析问题和解决问题的能力和情感意志等数学素养,因而成为数学高考中的一个必考热点[1].
随着教育公平的不断推进,2016年全国将有26个省(市)使用全国统一命题试卷,那么在这样的背景下,对于圆锥曲线这一必考内容,应如何备考以迎接即将到来的高考呢?在此对近六年的全国新课标卷的圆锥曲线考题进行初步分析,以期对备考有些许指导意义.
1.考题解读
1.1考题所涉内容分析。
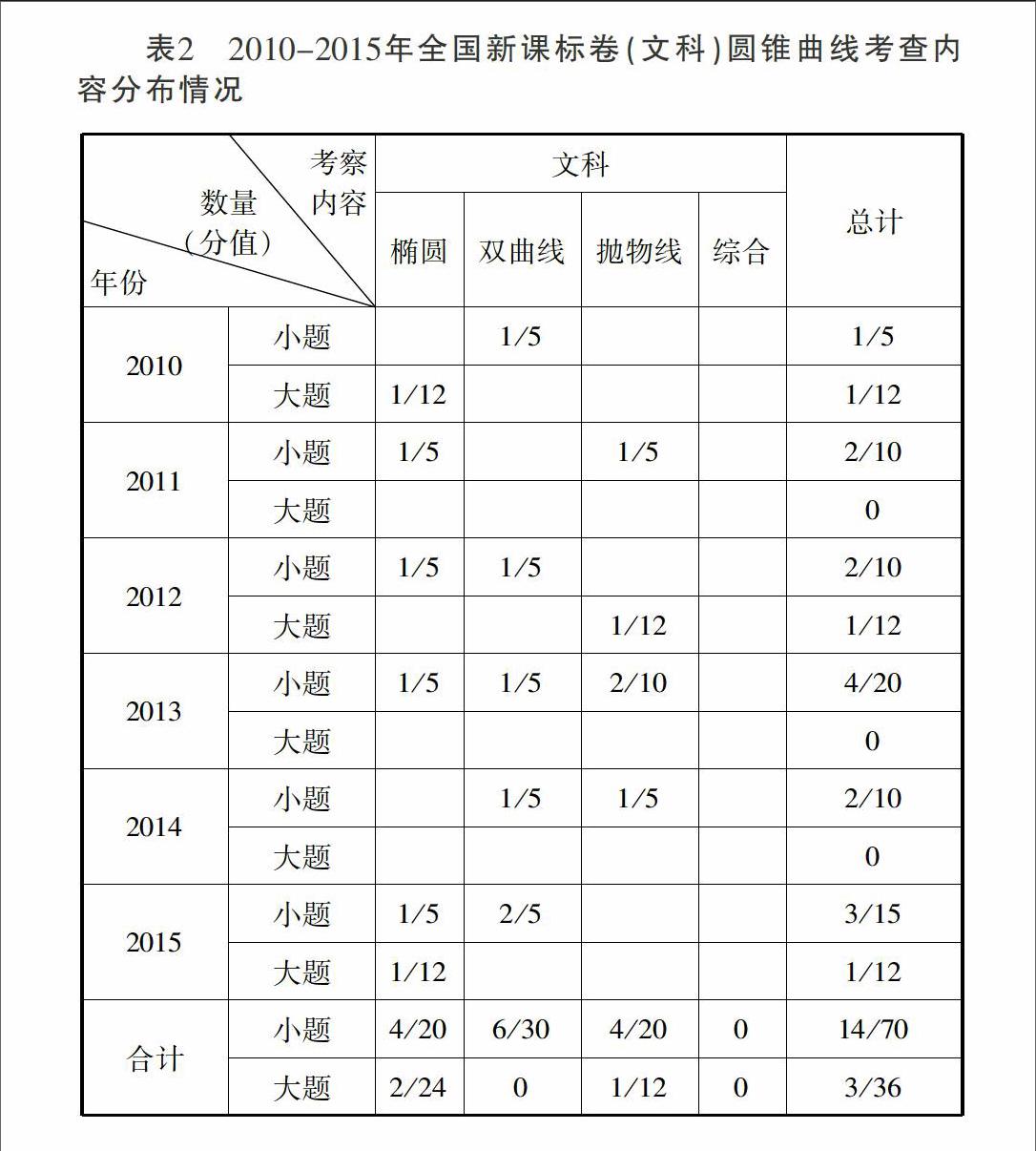
圆锥曲线的考查主要以椭圆、双曲线、抛物线及其中二者的综合为对象,考查形式主要有选择题、填空题和解答题三种形式,其中选择题与填空题、解答题在表1中分别以“小”、“大”代替.自2010年出现全国新课标卷以来,全国统一命题的新课标卷共18套,文、理各9套,其中2013、2014、2015年这三年每年有全国新课标卷Ⅰ、Ⅱ两套,2010、2011、2012年每年仅有1套全国新课标卷,其在圆锥曲线的考查对象上的数据如表1.
表1 2010—2015年全国新课标卷(理科)圆锥曲线考查内容分布情况
从表1和表2我们可以看出,在近六年的新课标全国卷中,从总体上看,无论是文科还是理科,对圆锥曲线的考查都是以椭圆为主要考查对象,在选择、填空、解答三种题型中均有分布,基本上以“两小一大”的方式考查,其中解答题共考查了8次,分值达94分之多,选择和填空共考查了8次,分值占40分,累计考查分数为134分;抛物线以解答题的形式考查了3次,分值为36分,以选择和填空的形式考查了8次,分值为40分,累计考查分数为76分;对于双曲线则全部以选择或填空题的方式进行考查,共12次,分值为60分.这无疑说明了全国新课标卷对双曲线、抛物线的要求大大降低了,同时又相应提升了椭圆的地位,这对我们的复习备考有着重要的指向作用[2].
1.2考题所涉具体知识点分析。
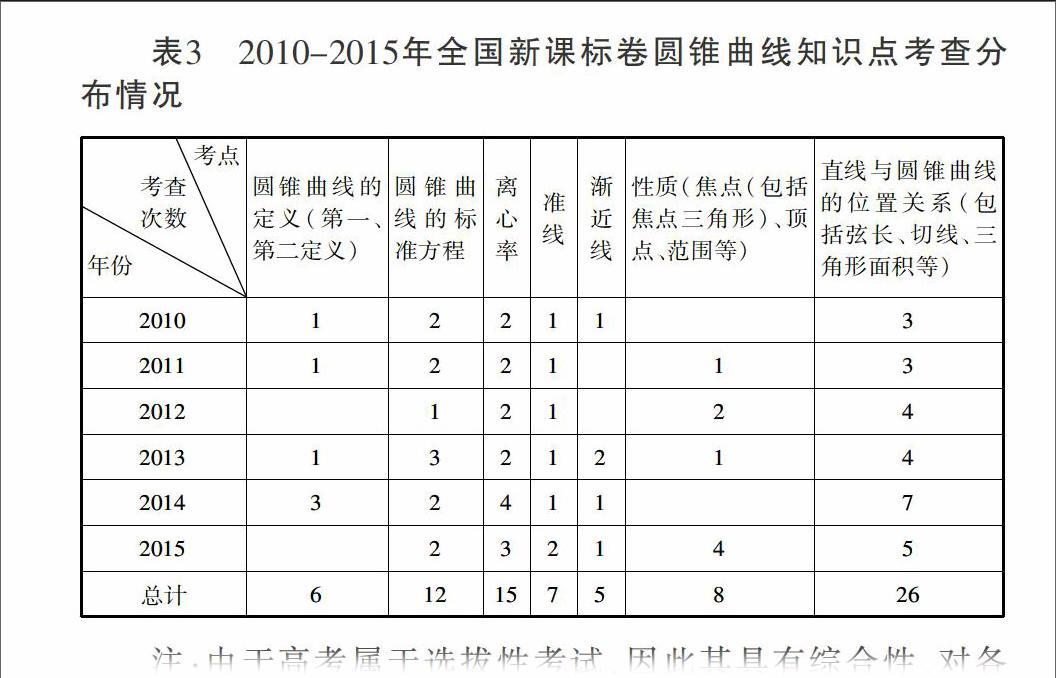
由于圆锥曲线的综合性较强,对它的考查往往与其他知识相结合进行,从总体上来看,其考查的知识点主要圆锥曲线的定义、圆锥曲线的标准方程、离心率、准线、渐近线、弦长公式、切线、直线与圆锥曲线的位置关系、点到直线的距离、两直线的位置关系、直线的倾斜角、斜率与方程、两直线平行或垂直、两点间的距离公式、点到直线的距离公式、三角形面积、平面向量等.在近六年的全国新课标卷中,对各部分知识的考查情况下如表2:
表3 2010-2015年全国新课标卷圆锥曲线知识点考查分布情况
注:由于高考属于选拔性考试,因此其具有综合性,对各知识点的考查往往以综合性为主,在圆锥曲线这一内容的考查上很少出现某单一知识点的考查,往往以知识点的综合、穿插的方式进行考查,因而表中所统计的知识点考查次数,会比实际考题数目多.其中未填数字的空格表示该考点在对应年份未考查到.
从表3中,我们可以看出,在近六年的新课标全国卷中,对圆锥曲线知识点上的考查,主要以圆锥曲线的离心率、圆锥曲线的方程、圆锥曲线与直线的位置关系为主,同时兼顾圆锥曲线的定义、准线、焦点等其他性质.这无疑对我们的备考方向有着重要的指示作用.
1.3考题意图分析。
在数学思想、数学能力层面,近六年的全国新课标试题中,主要对数形结合思想、函数与方程思想、分类讨论思想、转化与化归思想、整体思想;数学运算能力、推理论证能力、创新能力等进行了着重考查;在思维与能力的考查上,充分体现了“多考一些思维,少考一些运算”的命题理念,因而近六年全国新课标卷圆锥曲线大多数的解答题的运算量大大降低,但更突出了对数形结合思想、分类讨论思想、转化与化归思想等数学思想的考查,甚至在一些题目中,这些数学思想的运用与否直接决定了相应题目的解答速度与准确程度的高低.
例如:
(2015年新课标全国卷Ⅰ第20题)在直角坐标系xOy中,曲线C:y=与直线l:y=kx+a(a>0)交于M,N两点.
(1)当k=0时,分别求C在点M和N处的切线方程;
(2)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.
此题的第一个问虽然比较简单,计算量小,但它考查了学生的函数与方程的思想,通过导数方程求解.第二问是一个探索性问题,具有很强的开放性,其解法多样,但众多解法均离不开数形结合思想,转化与化归思想,以及分类讨论思想的应用;而且在本题中转化与化归思想的作用显得尤为突出.首先在解答过程中必须把“∠OPM=∠OPN”这一条件转化为代数表达式,其次要选择合适的转化方式(如转化为:“k+k=0”)才能减少计算量,使问题得到简化.
这样的例子不胜枚举,在此就不一一列举了.从这些例子可以看出,全国卷在圆锥曲线这一内容的考查上,更侧重数学思想方法的考查,在数学思想方法的考查中考查学生的数学能力,相对以前的试题,在计算量上有所降低,在思维量上有所上升,即“重思维,少计算”.
2.备考建议
通过前面对近六年全国卷圆锥曲线部分考题的粗略分析,从题型上看,可发现每年全国新课标卷对圆锥曲线部分的考查基本上都以一道选择、一道填空题、一道解答题,即“两小一大”的形式来考查,分值基本稳定在22分左右,个别年份有变动;从内容上看,解答题主要以考查直线与圆锥曲线的位置关系、圆锥曲线的方程为主,选择、填空则以考查圆锥曲线的性质(离心率、焦点、准线等)为主,其中圆锥曲线的离心率的考查又为之最,而且在各考查对象中,以椭圆为主,双曲线、抛物线次之,而且有抛物线、双曲线的考查主要以它们所具有的特殊性质为主;从考查意图上看,更重在对数学思维的考查,对计算能力的要求有所降低,题目更灵活.因此在备考中要注意以下几点:
2.1抓住重点,主次分明,有的放矢。
在复习备考中,要以椭圆为主,以抛物线、双曲线为辅;以椭圆的性质类比学习双曲线、抛物线的性质;通过类比和对比加深对椭圆、抛物线、双曲线的理解,还要着重强调抛物线、双曲线所具有的不同于椭圆的特殊性质及三者之间的联系.
2.2重视基础知识、基本性质的教学,培养基本技能。
在前面的分析中,我们可以看出,圆锥曲线的第一、第二定义考查高达6次之多,求圆锥曲线的标准方程共考查了12次,对圆锥曲线的基本性质考查更加突出,例如单单是离心率就考查了15次,渐近线、准线分别考查了5次、7次;这些都是圆锥曲线中最基础的知识要点,却在高考中反复出现,这无疑启发我们在复习备考中要重视基础,加强基础知识、基本性质的教学与训练.其次,由于圆锥曲线解答题的综合性较强,对思维能力要求较高,往往一下子看出思路,因此必须要求学生熟练掌握这些概念、性质及其之间的相互联系与区别,以为解题奠定坚实的基础、为思路的拓展做好准备.
2.3分类解析已考试题,总结方法规律、渗透解题思想。
教师要对近几年已考试题进行深入分析,将考查题型、知识点及解题思想等方面的共性加以总结,尤其要把不同题型的解题方式方法等策略性知识显性化,使学生能够在对题目的整体把握的基础上迅速理清解题思路、明确解题步骤,从而提高思维能力.如:定值定点问题、取值范围问题、最值问题、存在性问题等各自均有不同的处理方式、不同的解答思维,老师要对近几年高考题进行分类解析,总结其中具有规律性的解题思路.其次,要对各考题中思想方法进行渗透,如:直线与圆锥曲线位置关系的题目中要利用对直线斜率的讨论、存在性问题中对一些特殊情况的讨论题目等渗透分类讨论的数学思想,在圆锥曲线的几何关系与代数关系的转化中渗透转化与化归思想、数形结合思想,在圆锥曲线计算推理中渗透整体思想、设而不求的数学方法等.
2.4注重知识综合,强调交叉渗透。
圆锥曲线这部分内容的考查中常常以综合性考法为主,很少出现对单一知识点的考查,因而在教学中不仅要使学生掌握圆锥曲线的单个知识点,更要让学生理解各知识点之间的内在联系与区别及运用这些知识解题的思维过程.还要以圆锥曲线知识为主线联系其他相关知识(如:向量、函数、不等式、直线方程、平面几何等),使学生所学知识形成一个相互联系的有机整体,从而促进思维能力的发展.相反,如果过于强调各知识点之间的相对独立性,就会导致相关知识间的相互割裂,学生对知识的理解仅限于单一的知识点上或者限于对知识结论的记忆上,不能做到举一反三、融会贯通,当然,这样就达不到新课标的要求.
参考文献:
[1]王草野.圆锥曲线学习中存在的问题及对策研究[D].江苏:苏州大学,2014.
[2]徐燕.高中生对圆锥曲线的理解[D].上海:华东师范大学,2009.
