用割补法巧解一类几何题

⦿陕西省西安市田家炳中学 冯恒仁

1 割补法的内涵

所谓割补法就是把一个复杂图形的长度、角度、面积或体积的计算分割成若干个简单图形的有关计算，或者将一个不易求出长度、角度、面积或体积的几何图形补形为较易计算的几何图形.例如，把梯形割补成平行四边形、矩形、直角三角形，把斜三角形割补成直角三角形，把斜棱柱割补成直棱柱，把棱锥补成棱柱(常见的题是将特殊的三棱锥、四棱锥补形为长方体、正方体)，把多面体切割成锥体，把不规则的几何体割补成规则的几何体，从而把复杂的转化为简单的、把不够直观的转化为直观易懂的.

2 割补法在解题中的应用举例

2.1 在平面几何中的应用

例1如图1，在梯形ABCD中，AB∥CD，AB=5，BC=3，CD=1，DA=2，求梯形的面积.

分析：要求梯形的面积，就要求其高，进而就要求其一个内角.因此，过一个顶点作一条腰的平行线，把其分割为平行四边形和三角形，再作三角形的高，把三角形分割为直角三角形，由正弦函数的定义求出高.

图1 图2

解：如图2，过点C作CE∥DA，交AB于点E，再过点C作CF⊥AB，垂足为F.

∵DC∥AE，CE∥DA，

∴四边形AECD是平行四边形.

∴CE=DA=2，AE=DC=1.

∴BE=AB-AE=4.

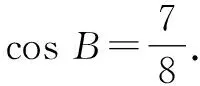
点评：梯形面积计算问题，辅助线的作法一般有两种，一是过顶点作高，把梯形分割成直角三角形和矩形，还有一种就是过顶点作另一腰的平行线，把梯形分割为平行四边形和三角形.本题两种方法都用到了.

例2如图3，分别以边长为1的正方形ABCD的顶点B，C为圆心，1为半径作圆弧AC，BD交于点E，求曲边三角形ABE的面积.

分析：连接BE，EC，把曲边三角形ABE的面积转化为扇形ABE的面积减去弓形BE的面积.

图3 图4

点评：求弓形面积时，割补法是学生很容易掌握的一个典型的技巧.

图5

(2)方法1：方程(组)法[1].

sinθ=2cosθ.

点评：充分利用正弦定理、余弦定理，列方程(组)，解方程(组)，属于常规解法.虽然运算量有些大，但中规中矩，思路清晰，不难掌握.

方法2：补形法.

图6

点评：通过补形，转化为特殊的三角形，虽然还是用正弦定理、余弦定理求解，但与方法1比较，运算量较小.

方法3：分割法.

如图7，过点C作CN⊥AD,垂足为N，过点B作BM⊥CN,垂足为M.

由已知得，四边形ABMN是矩形.

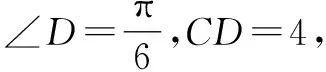
又MN=AB=1，则CM=1，BM=1.

点评：与方法2相比，方法3运算量更小.

图7 图8

方法4：割补法.

如图8，分别延长CB,DA,设CB∩DA=E,过点C作CN⊥AD,垂足为N.

由已知可得△ABE和△NCE都是等腰直角三角形，且AE=AB=1.

点评：与方法3相比，方法4更简洁，只要把题目中的弧度改为角度，初三学生都可以很快算出结果.

2.2 在立体几何中的应用

例4已知正四面体A-BCD的棱长为a，求该正四面体的外接球的表面积和体积.

图9

分析：如图9，将正四面体A-BCD补成正方体.则正方体的面对角线长为a，正方体的外接球就是正四面体A-BCD的外接球.

解：如图9，将正四面体A-BCD补成正方体，正方体的外接球就是正四面体A-BCD的外接球.

例5已知直三棱柱ABC-A1B1C1中，∠ABC=120°，AB=2，BC=CC1=1，求异面直线AB1与BC1所成角的余弦值[2].

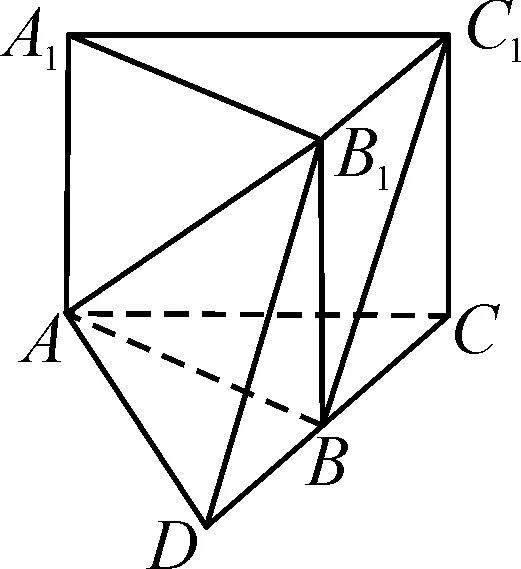
图10

解法1：如图10所示，延长CB至D，使BD=BC，连接AD，B1D.

∵B1C1∥BD，B1C1=BD，

∴四边形B1C1BD是平行四边形.

∴C1B∥B1D.

∴∠AB1D或其补角为异面直线AB1与BC1所成的角.

在△ABD中，由余弦定理，得

AD2=AB2+BD2-2AB·BD·cos∠ABD=3.

点评：对于两条异面直线所成的角，可固定一条，平移另一条，或两条同时平移到某个特殊的位置.本题是固定一条，平移另一条，把两条异面直线所成的角转化为两条相交直线所成的角，再通过解三角形求之，属于常规解法.

图11

解法2：如图11，将直三棱柱ABC-A1B1C1补形为直四棱柱ABCD-A1B1C1D1，连接AD1，B1D1，BD.

在△ABD中，由余弦定理知

BD2=22+12-2×2×1×cos60°=3.

因为AD1∥BC1，所以直线AB1与AD1所成的角即为直线AB1与BC1所成的角.

点评：将直三棱柱ABC-A1B1C1补形为直四棱柱ABCD-A1B1C1D1，异面直线AB1与BC1所成角更容易找到.

3 总结

巧妙利用割补法求解一些几何问题，关键是根据已知条件将原图形通过分割或补形转化为规则图形或特殊图形，从而使问题简单化，这一过程也充分体现了化归与转化思想.