借助隐圆解决向量问题 直观想象彰显魅力
2022-04-16上海市市西中学庞良绪
中学数学 2022年19期
⦿上海市市西中学 庞良绪
《普通高中数学课程标准(2017年)》指出,直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决问题,主要表现为:建立数与形的联系,利用几何图形描述问题,借助几何直观理解问题[1].平面向量具有几何与代数的“双重身份”,加之解法灵活多样,备受命题者的青睐.纵观历年的高考及模拟试题,它们大多数都有优美的几何背景,因此,若能透过向量语言把握其几何直观,尤其其中一些试题若能挖掘出隐含的圆,可以避免复杂的代数运算,能使问题快速获解.下面举例说明.
1 半径圆




图1 图2


2 直径圆


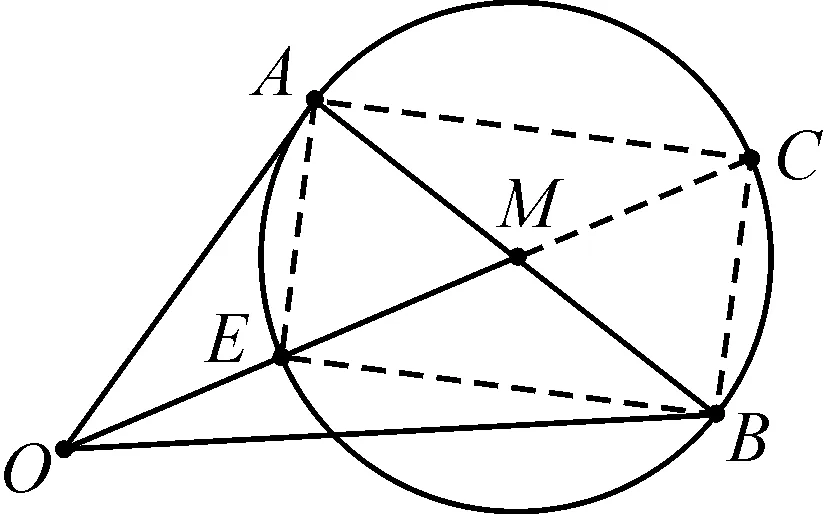
图3

例4已知向量a,β是平面内两个互相垂直的单位向量,且(3α-γ)·(4β-γ)=0.则|γ|的最大值为.

图4

3 四点圆
若四边形ABCD对角互补,则A,B,C,D四点共圆.



图5


4 极化圆




图7
5 阿波罗尼斯圆



上述介绍了借助隐圆解决平面向量问题,需要指出的是,在问题解决的过程中,并不是追求高难度的解题技巧,而是着眼于对数学问题和数学本质的理解,在重视几何直观的同时,也不能忽视代数运算.要引导学生达成“脑中有形”(亦即数学抽象、直观想象),心中有数(亦即逻辑推理、数学运算),手中有术(亦即数学建模、数据分析)[2].
