一题多解玩转二次根式证明题

⦿重庆市永川北山中学校 吴治新

我们将根号下含有字母的代数式叫作无理式，对于无理式的证明题，单靠二次根式的有关性质进行运算很难奏效，还需注意分析题意，根据题目特点结合适当的方法与技巧.下面以一道二次根式证明题为例作简要分析.

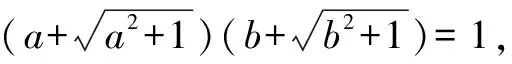
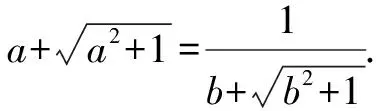
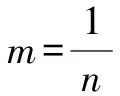
方法一：改写并化简等式，从轮换式特点去整体相加.

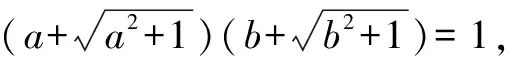
①

同理，得

②

①+②，得

整理，得a+b=-(a+b).

所以a+b=0得证.

点评：从倒数的意义入手，根据等式的性质改写已知等式，成为几个式子和的形式，再利用轮换式特点，将改写后的式子整体相加，则隐含关系明了，问题获解.

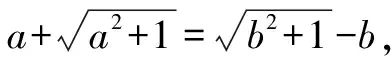
方法二：改写并化简等式，两边平方.

证明：由已知，得

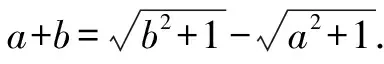
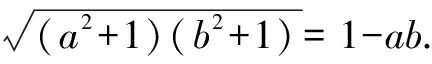
两边再平方，得(a2+1)(b2+1)=1-2ab+a2b2.

整理，得(a+b)2=0.

所以a+b=0得证.

点评：利用倒数性质改写已知等式，再两次平方，并运用乘法公式运算，将无理式转化为整式.根据等式的性质，两边平方，将无理式化为有理式，也是解决无理式问题的常见策略.

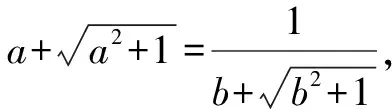
方法三：将等式两边同乘有理化因式.

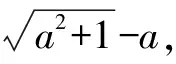
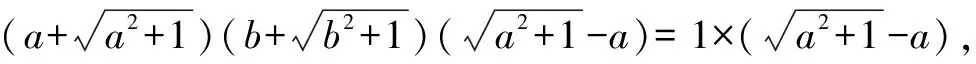
③

④

③+④,得a+b=-a-b.

则2(a+b)=0.

所以a+b=0.

点评：将已知等式乘有理式因式，就可以将二次根式的积转化为二次根式和的形式.在证明二次根式一般过程中，由因导果，从化简条件入手，恒等变形的基本方法往往是有理化.

分析4：换元法是解数学题的一种重要方法，用某一字母代换已知等式中较长的式子或结构复杂的式子，使条件简明，将问题化繁为简.

方法四：换元 + 平方.

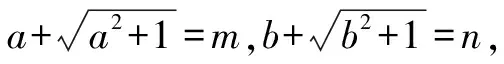
两边同时平方，得

(m-a)2=a2+1，(n-b)2=b2+1.

又mn=1，所以

m2-2am+a2=a2+mn，

n2-2bn+b2=b2+mn.

即

m-2a-n=0

⑤

n-2b-m=0

⑥

⑤+⑥，得a+b=0.

点评：用换元法建立两个等式，并将等式平方，去掉根号，得到与a，b有关的有理式，再运用轮换式的特点，进行整式运算，问题得以解决.

方法五：换元+分式化简.

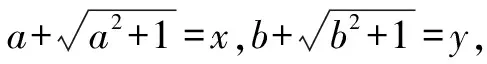
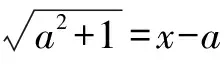
a2+1=x2+a2-2ax.

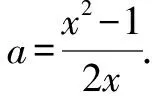
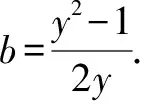
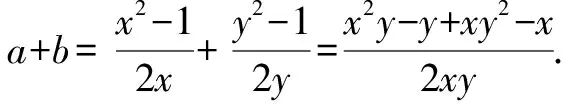
又xy=1，所以a+b=0.

点评：用换元法将原问题增设两个变量，两边平方后，将无理式问题转化为有理分式问题，运用有理式的运算法则进行计算求解.

方法六：换元+取倒.

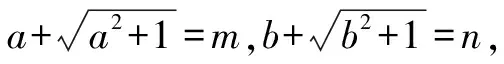
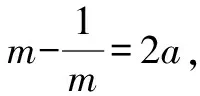
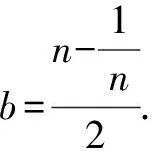
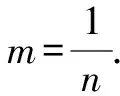
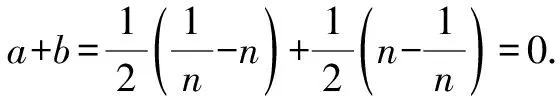
点评：设元使原问题增加了两个变量，通过“求倒”得到与a或b有关的两个式子，且这两个式子互为相反数从而快速求解.

方法四～六用换元法解题，其目标是将无理式问题转化为有理式问题，通过换元得到两个等式，并进行恰当的运算，使复杂问题简单化，达到转化求解的目的.

将上面例题改编，得到一组题目，让我们一显身手吧.

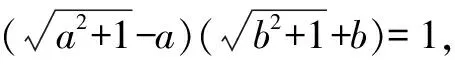
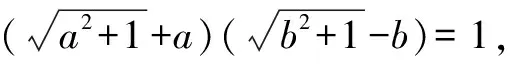
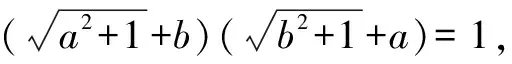
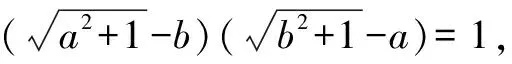
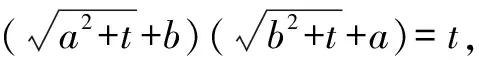
创新是一个民族进步的灵魂，培养学生的创新思维和创新能力，是现代教育的出发点和归宿.因此，在数学教学中发展学生的创新思维，是时代的要求，也是课程标准提出的要求，更是学生发展的需求.如何培养学生的创新思维？“一题多解”是最平常，也是力所能及的的课堂教学手段.例如，本文中的例题，是一道二次根式的证明题，在平时学习中较少碰到，利用一般的方法无从破解，但若从题目已知条件的特征及结果形式分析，发现与“倒数”及“轮换式”等知识点有关，可结合二次根式、整式、分式的运算法则及性质进行计算推理，得出答案.方法一，从轮换式特点去整体求解；方法二，从倒数性质入手，运用平方法去根号，运用乘法公式求解；方法三，结合二次根式特点，两边乘有理化因式，达到转化目的；方法四～六利用换元法，增加变量，利用完全平方式、分式化简进行恒等变形.以上几种证法，贯穿了二次根式化简的常用方法，较好地发展了学生的创新思维，有利于启迪学生思维，开阔学生视野，为学生熟练掌握数学基础知识，训练数学基本技能，领悟数学基本思想方法，积累数学基本活动经验，打下坚实基础，切实提高学生分析问题和解决问题的能力，提高数学素养.Z