分步突破精准切入 策略总结典例探究——以一道函数与几何综合题为例

⦿江苏省苏州高新区实验初级中学 张 玲

1 考题呈现

考题(2021年江苏无锡市中考卷第27题)在平面直角坐标系中，点O为坐标原点，直线y=-x+3与x轴交于点B，与y轴交于点C，二次函数y=ax2+2x+c的图象过B和C两点，且与x轴交于另一点A，点M为线段OB上的一个动点，过点M作直线l平行于y轴交BC于点F，交二次函数y=ax2+2x+c的图象于点E.

(1)求该二次函数的表达式；

(2)当以C，E，F为顶点的三角形与△ABC相似时，求线段EF的长度；

(3)已知点N是y轴上的点，若点N，F关于直线EC对称，试求点N的坐标.

2 分步突破

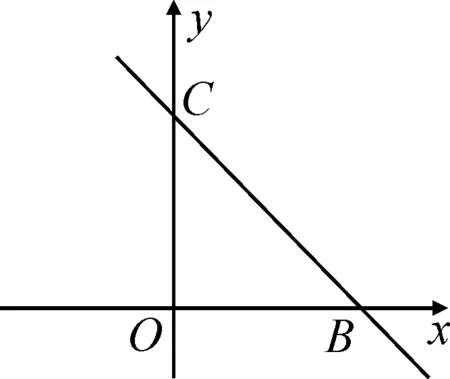
图1

本题目为函数综合题，以抛物线与直线为背景，依托坐标系中的点构建三角形，所设三问全面考查学生的基础知识和综合能力.第(1)问求函数的解析式，考查待定系数法；第(2)问由三角形相似，考查函数中的相似构建；第(3)问则是关于点的对称，考查对称转化.下面结合具体函数的图象，分步突破.

2.1 第一步——待定系数法求解

二次函数y=ax2+2x+c中需求a和c的值，只需求抛物线上点B和C的坐标即可.由于两点是直线y=-x+3与坐标轴的交点，故可直接求得.

2.2 第二步——构建相似模型

该问探究以C，E，F为顶点的三角形与△ABC相似，需要关注问题中的两点：①题干没有给定相似对应关系，需要分类讨论；②关注两三角形的角度关系.

图2

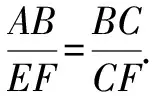
2.3 第三步——对称转化推理

第(3)问是函数背景下的几何对称问题.求对称点N的坐标，有两点要求：(1)点N位于y轴上，则其横坐标的值为0；(2)点N和F关于直线EC对称，则它们到直线EC的距离相等，可依托该特性构建几何关系.

图3

3 解法探究

上文对一道抛物线综合题进行了分步突破，分别求解函数的解析式，探讨三角形相似关系，分析点的对称.从本质上看，考题为函数与几何综合题，掌握函数背景中几何图形的探究方法是解题的关键.下面对问题解法进行深入探究.

3.1 函数背景下的三角形相似

上述考题第(2)问探究三角形的相似问题，有两大特点：一是没有设定对应关系，二是两三角形含有特殊对应角(45°角).故需要讨论三角形的相似对应，且只需求两种情形.通常对于函数背景下的三角形相似问题，可以采用如下策略，分三步论证.

第一步，假设结论成立，分情形讨论.

对于没有明确对应关系的相似三角形问题，可先设定分类标准，再分析所涉三角形是否含有特殊对应角.若有，则提取对应角，再分类；若没有，则分别讨论三种对应情形.

第二步，设未知，求线段或边长.

对于三角形相似问题，可从角度和边长对应成比例两个视角突破，但在函数背景下，采用边长对应成比例更容易构建等式.解析时，可设定关键点的坐标，推导相关线段或边长.

第三步，建方程，精计算.

根据相似三角形对应关系列比例式，将比例式中的线段用含点的坐标参数的线段替换，进而构建含有坐标参数的方程，通过解方程精准求解.

基于上述解题策略，下面对例1进行进一步探究.

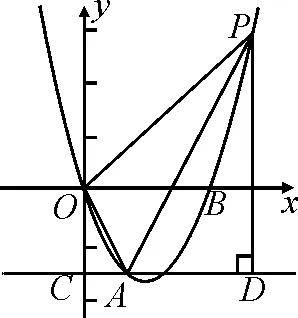
图4

(1)求该抛物线的解析式；

(2)在抛物线上取一点P，过点P作直线AC的垂线，设垂足为点D，连接OA，使以点A，D，P为顶点的三角形与△AOC相似，试求出对应点P的坐标.

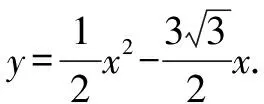
(2)因为△AOC为直角三角形，故以A，D，P为顶点的三角形也必须为直角三角形.故点C始终对应点D，只有△OCA∽△ADP和△OCA∽△PDA两种情形.同时需要分点P位于直线AD上方和下方两种情形.

①若点P在直线AD上方，则

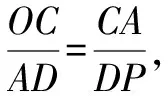
当点P(0,0)时，也满足△OCA∽△PDA.

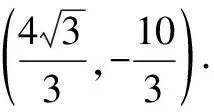
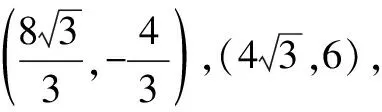
3.2 函数背景下的点对称

上述考题的第(3)问求两点关于直线对称时其中一点的坐标，属于函数背景下的点对称求坐标的问题，相对于常规的几何问题，函数背景为问题赋予了“数”的特性.通常可将问题分为三种情形：一是关于坐标轴或平行于坐标轴的直线对称；二是关于特殊直线对称，如y=x；三是关于一般直线对称.前两种情形，对称关系有着鲜明的坐标规律，在数值和符号两方面均有体现.而对于情形三，则可以采用下面三大策略来解.

3.2.1 中点坐标公式

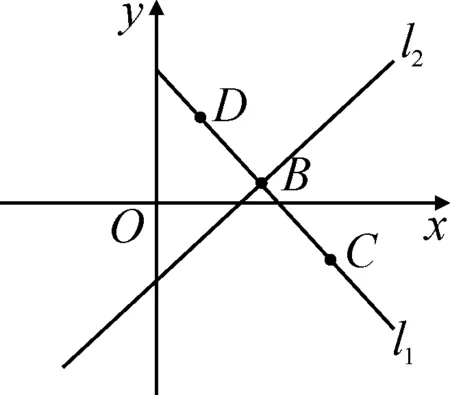
图5

连接两对称点，则两点所在直线与对称轴所在的直线为垂直关系，且两直线的交点为两对称点连线段的中点，三点坐标满足中点坐标公式.以图5为例，点C和D关于直线l2对称，且位于直线l1上，则直线l1和l2的斜率之积为-1，B为线段CD的中点，则xD+xC=2xB，yD+yC=2yB.

3.2.2 点到直线的距离公式

根据对称性可知，两对称点到对称轴的距离相等.故对于已知曲线或直线上点的对称问题，可设出该点的坐标，然后利用点到直线的距离公式构建方程求解.以图5为例，若点D满足方程y=kx+b，且已知点C的坐标及直线l2的方程，则可设点D(x，kx+b)，先求出点C到直线l2的距离，再利用距离公式构建点D到直线l2的距离方程，进而求解.

3.2.3 构建全等模型

两点关于某一固定直线对称，则可依托直线上固定两点构建全等三角形，后续通过求线段长求解.另外，也可通过几何推导求线段长确定所求点的坐标.

上述考题第(3)问在求解时就采用了该方法，下面结合一道例题进一步强化巩固.

图6

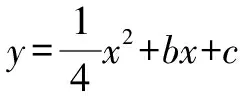
(1)求该抛物线的解析式；

(2)求点A关于直线y=2x的对称点A′的坐标，并判断点A′是否位于该抛物线上.

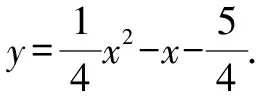
图7

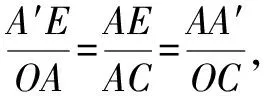
4 写在最后

上述对一道函数与几何综合题开展分步突破，并探究问题的解法，其中三角形相似与点的对称属于典型问题，问题的“数”“形”属性十分突出.数形结合分析，几何视角切入，运算推理定位，是破题的有效策略.教学中，建议引导学生把握图象的特征，提取特殊图形，结合特性推理，充分拓展学生的解题思维.