分式的基本性质易错点及避错策略分析

⦿临夏县河西乡大庄中心小学 刘自鹏

1 引言

结合当前学生“分式的基本性质”的学习情况，本文中首先阐述分式的基本性质，然后以几道错题为例，在对其分析后提出相应的避错策略.希望这样的分析与研究，能给一线教师教学提供更多思路，能帮助学生拨云见日.

2 阐述分式的基本性质

2.1 分式的基本性质

分式的分子与分母都乘或除以同一个不等于零的整式，分式的值不变.用字母可表示为：

在理解时要注意以下几个方面：

第一，该性质应用于分式的变形时属于恒等变形，它不改变分式的值的大小[1].

第二，如果原分式的分子或分母是多项式，那么原分式的分子和分母都应先放入括号中.

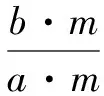
第五，分式的基本性质在应用时一定要做到“两同”，即分子分母同乘或同除以一个整式，且该整式必须不为零.这“两同”缺一不可[2].

2.2 分式的符号法则

分式的符号可谓非常灵活多变.在不改变分式大小的情况下，分式的符号变化主要分为以下两类：

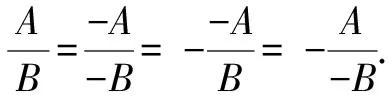
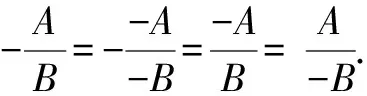
例1下列分式运算中正确的是( ).

解析：根据分式的基本性质来判断.

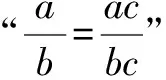
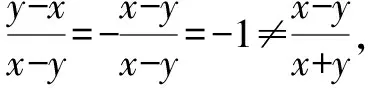
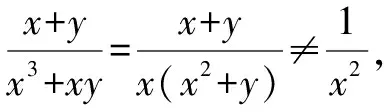
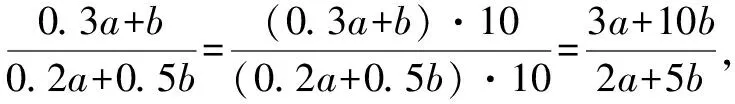
故选答案：D.

例2利用分式的基本性质填空：

分析：根据分式的基本性质在应用时的注意事项，首先应对原分式进行因式分解，然后将“分式的分子分母同时乘或除以一个不为零的整式”的中间步骤写出来，最后得到正确结果.

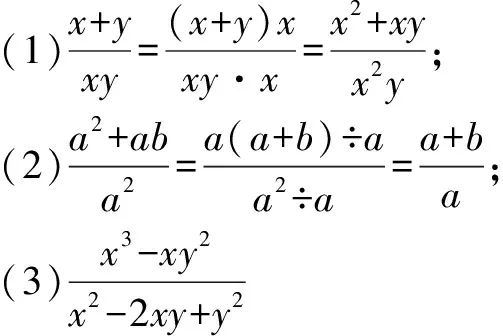
3 错题例析

学生在利用分式的基本性质时，容易在以下几个方面出错.

3.1 忽略“乘或除以一个不为0的整式”

例3下列变形中正确的有( ).

错解：选D.

解析：错解中忽略了x+y，m可能为零的情况.在利用分式的基本性质时，分子分母所乘或除以的那个整式一定不能为零.而(2)(4)之所以能计算，是因为分母中分别隐含了ab≠0，a-4≠0的条件.

正解：选B.

3.2 忽略“分子分母同乘或除以一个不为0的整式”

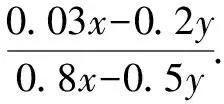
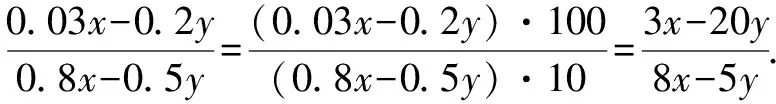
分析：分子分母同乘或除以一个不为0的整式，是使用分式的基本性质时应遵循的最基本的条件.所以，分子分母应同时乘以100.

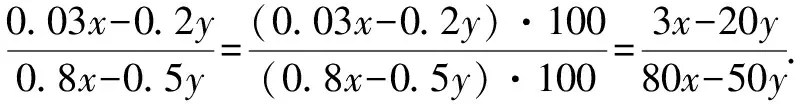
3.3 少括号

例5若x，y的值均扩大为原来的3倍，则下列分式的值保持不变的是( ).

错解：选B.

分析：解这类问题应该先求出变化后的分式，然后与原分式进行比较.当然，在代入x或y的3倍时，应将3x或3y放入小括号中.

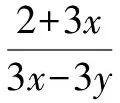
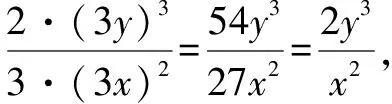
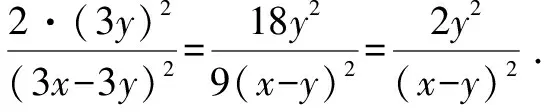
故选答案：D.

4 避错策略

在使用分式的基本性质时需注意许多地方，那么如何在使用时避免出错呢？接下来结合一线教学经验提出一些策略.

吃透性质，抓准关键字.分式的基本性质内容简单，要想吃透需抓住如下这些关键字：

“都”.这说明分子和分子是同时乘或除以某个整式，而不是只有分子或分母单独进行.

“同”.这说明分子和分母都乘或除以同一个整式，该整式是同一个，不能像例4中错解一样.

“不等于零”.时刻注意分母不等于零，是掌握与分式有关知识点的关键.

“整式”.虽然目前这方面错误极少，但也应注意.

为了让学生抓准这些关键字，教师不仅要在讲解概念的时候圈出关键词，而且有必要解题时提醒学生将解题过程与这些关键字一一对应[3].笔者在实际教学中，要求学生将这几个关键字写在一张纸上，每解完一题都与之对比.

养成检查的良好习惯.解决数学问题需要良好的检查习惯，为此笔者让学生在试卷或草稿纸中央写好“要检查”三个字，并在检查后将之打勾.如此操作一段时间后，学生检查的意识比以前更强.

5 结语

分式的基本性质是后续诸多知识点的基础，掌握好这一知识点是学好分式这一章乃至与其有关知识点的重要前提.所以，教师要注重知识点的细讲，特别是学生容易出错的地方，一定要让学生加强练习.这样一来，学生才能更好地掌握知识点，才能在运用过程中更少出错.