例谈初中数学“优化问题设计”的教学思考

⦿聊城市实验中学 于冬梅

1 引言

有效的教学活动是学生学与教师教的统一，课堂教学要充分发挥教师的主导作用，充分落实学生的主体地位[1].“体验不深切、理解不深刻、思维不深入、发展不深远”是当前初中教学的普遍现象[2].“问题引领”则是改善上述现象的有效手段或途径.当前课堂教学中，教师大都认识到了“问题引领”对学生发展的重要性，好的问题设计不仅可以帮助学生更好地理解和运用知识，主动构建知识体系，也是启迪学生思维、提升思维品质和素养的重要方式.这就要求一线教师提升“设问”的专业素养.基于此，笔者把青岛版“反比例函数图象”教学的两种问题设计整理成文，与读者交流分享.

2 问题设计的教材背景分析

反比例函数是继一次函数后，知识与方法上的一次水平迁移，理解与认知上的一次提升.图象和性质是函数研究的重要内容，研究方法可以类比一次函数，先由描点法画出反比例函数的图象，并通过图象来探索确定反比例函数的性质.图象由“一条”到“两支”，形态由“直”到“曲”，由“连续”到“间断”，由与坐标轴“相交”到“渐近”，无不折射出对反比例函数本质属性认识的进一步深化.

反比例函数的图象和性质，蕴含着丰富的数学思想.首先，反比例函数的图象和性质，本身就是“数”与“形”的统一.通过对图象的研究和分析，可以确定函数本身的性质，体现了数形结合的思想方法.这在学习数轴、平面直角坐标系时，学生已经接触过，结合本课内容，可以进一步加强对数形结合思想方法的理解，发挥从“数”和“形”两个方面共同分析解决问题的优势.其次，从本节课知识的形成过程来看，由“解析式(确定自变量取值范围)”到“作图(列表、描点、连线)”，再到“性质(观察图象探究性质)”，充分体现了由“数”到“形”，再由“形”到“数”的转化过程，这种函数解析式及性质与函数图象之间的联系，突出体现了二者间的转化对分析解决问题的特殊作用，是转化思想的具体应用.

3 问题设计的学情背景分析

学生已经学习了平面直角坐标系的相关知识，学习了一次函数的概念、图象、性质与应用，经历了一次函数的研究过程，了解了一次函数的研究方法，同时上节课通过具体情境体会了反比例函数的概念，已经具备了继续研究反比例图象的知识储备和能力储备.

4 教学问题设计与思考

4.1 比较教学流程中的两种设计

第一种设计:

问题1一次函数的图象及其性质是怎样研究的？

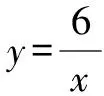
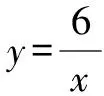
问题4在x≠0的范围内，选定自变量x的值，计算出对应的y值，完成表格.

问题5完成表格后，怎样描点连线呢？

问题6反比例函数的图象能不能用折线段连接？比如相邻两点A(1，6)与B(2，3)之间，能不能用线段来连接？为什么？如果不能，应该怎样连接？

问题7想一想，图中能用线段或平滑的曲线将点(-1，-6)与点(1，6)连接吗？为什么？

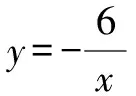
第二种设计:

问题1知道反比例函数的概念后，你认为再研究反比例函数的哪些知识？

追问：关于函数图象的研究，你具备什么方法和经验呢？

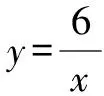
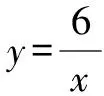
追问1：自变量x可以取值的范围是什么？

追问2：列表时你会选取哪些自变量x的值呢？

追问3：反比例函数的图象能不能用折线段连接？比如相邻两点A(1，6)与B(2，3)之间，能不能用线段来连接？为什么？如果不能，应该怎样连接？

追问4：想一想，图中能用线段或平滑的曲线将点(-1，-6)与点(1，6)连接吗？为什么？

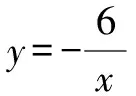
4.2 关于两种问题设计的思考

通过比较可以发现，同样是八个问题，第一种设计问题较为细碎，把学生的思维束缚在一个狭小的范围内，沿着教师的思维亦步亦趋进行思考，虽然教学比较顺利，但是不利于学生思维能力的发展.

对比分析第二种设计，问题1和问题2两个大问题给学生提供了足够大的思维空间，也给学生提供了产生疑惑和提出问题的机会，有利于发展学生发现问题、提出问题的能力，同时也有助于学生自主构建函数学习的一般思路，提升思维的系统性.把第一种设计的部分问题调整为追问的问题，是在必要的时候给需要的学生必要的帮助，将学生的思维不断引向深处，提升思维的严谨性.具体有以下几点优势.

4.2.1类比优化研究方法

知识的迁移指的是一种知识对另一种知识的影响，温故而知新，是学生在学习活动中表现出来的一种迁移能力素养.第二种设计的问题1，由学生自主回忆曾经经历过的一次函数图象的研究过程，并类比确定反比例函数图象的研究思路，有助于学生自主构建函数学习的一般思路.

4.2.2 猜想提升教学价值

函数图象的教学价值绝不仅仅是列表、描点、连线画图这样的技术活，画图之前，学生根据函数表达式猜想判断图象的大致形状、特征，是智力层面的思维活动，远高于技术层面，也体现了教师的教育智慧[3].第二种设计增加了根据反比例函数解析式先猜想图象再自主画图的两个大问题，给学生营造了独立动手动脑足够大的思维空间，学生在猜想判断图象的大致形状特征和具备一次函数画图经验的基础上，可能出现直的图象或与坐标轴相交的图象等错例，不仅为后续的研究作了铺垫，也在后续的研究中激发学生思维的涟漪.

4.2.3 追问引领思维深入

第二种设计的问题2和3两个大问题给学生提供了足够大的思维空间，也给学生提供了产生疑惑和提出问题的机会，有利于发展学生发现问题、提出问题的能力.把第一种设计调整为追问的四个问题，是在必要的时候给需要的学生必要的帮助，将学生思维不断引向深处；再结合教师的精讲点拨与《几何画板》演示，可以帮助学生纠正思维的误区，完善思考过程中不严谨之处，提升思维的严密性.

4.2.4 迁移提升应用能力

知识迁移的实质就是触类旁通、举一反三，就是把学到的原理知识应用到新的知识或者解决问题当中去.第二种设计问题4就是给学生提供应用所学知识技能完成新的学习任务的机会，由学生自主画图象并根据图象分析归纳k<0时反比例函数的性质，帮助学生实现知识技能的水平迁移，促进知识体系的自主建构.

5 结语

初中数学教学中设计具备思维的进阶性、促进学生深度学习的问题，有利于学生对知识的逐步抽象与建构，有利于学生形成完整的思维结构，也有利于学生数学活动经验的积累.