光学轨道角动量复用纠缠源的实验产生及其应用

徐笑吟,刘胜帅,荆杰泰,2,3∗

(1华东师范大学精密光谱科学与技术国家重点实验室,上海 200062;2中国科学院超强激光科学卓越创新中心,上海 201800;3山西大学极端光学协同创新中心,山西 太原 030006)

0 引言

1992年,Allen等[1]在理论上确认了光子除了具有自旋角动量外,还有轨道角动量(OAM)。与光子的自旋角动量不同,轨道角动量的轨道量子数可以取任意整数,可以利用光子的轨道角动量构建一个高维的希尔伯特空间,因而光学轨道角动量可以成为高维经典信息和量子信息的载体[2]。另外,由于带有轨道角动量的光束具有螺旋波前、环状光强分布以及轨道角动量的不同模式之间相互正交等特性,其在经典通信、量子通信和粒子操控等领域有着十分广泛的应用。例如,由于轨道角动量光束的螺旋结构和暗中空特性,可以用它对微粒进行束缚和操控[3,4]。此外,由于不同的光学轨道角动量模式是相互正交的,光学轨道角动量可以作为一种自由度来实现经典信息的编码和传输[5-7]。同时,在量子体系中,光学轨道角动量也可以作为一组正交基矢来构建无限维度的希尔伯特空间。通过在光学轨道角动量这个自由度上进行编码,可以实现量子信息的传输[8-10]。

在离散变量量子体系中对光学轨道角动量的研究十分广泛,例如:产生基于光学轨道角动量的双光子和多光子高维纠缠[10-12],利用光学轨道角动量实现单光子多自由度的量子隐形传态[9],在两个量子存储器之间实现基于光学轨道角动量的多自由度纠缠[13],实现光的多个轨道角动量态的纠缠交换[14],以及产生窄带宽光学轨道角动量和偏振超纠缠光子[15]。但在连续变量量子体系中对光学轨道角动量的研究还比较少。在连续变量量子体系中,常常用光学轨道角动量来产生具有光学轨道角动量模式的量子态。例如:2008年,Lett研究组基于四波混频过程制备出光学轨道角动量模式的孪生关联光束,并证明了其强度的量子关联特性[16,17];2009年,Andersen研究组基于四波混频过程实现了一阶光学轨道角动量模式的连续变量纠缠[18];2014年,山西大学郜江瑞研究组利用光学参量振荡器产生了偏振和光学轨道角动量模式的连续变量超纠缠[19]。目前,已经证明基于热铷原子系综的四波混频过程是产生连续变量纠缠的有效手段[20-24],而利用光学轨道角动量可以实现纠缠通道数的增加,将光学轨道角动量与四波混频过程产生的纠缠结合则可以制备出光学轨道角动量复用的纠缠源,从而发挥光学轨道角动量高阶模式的优势,进而提升量子信息体系的信息容量,也为连续变量量子信息的发展提供了新的研究平台。

本文简单介绍了光学轨道角动量的基本概念,并从光学轨道角动量复用纠缠源的制备及其在量子信息领域的应用两个方面综述了本课题组将光学轨道角动量复用与基于四波混频过程的连续变量纠缠系统相结合的研究成果。

1 光学轨道角动量的基本概念

拉盖尔高斯光束可以携带轨道角动量,光强分布呈现出环形的特点,且不同的轨道角动量模式间相互正交。在傍轴近似下,柱坐标系下拉盖尔高斯光束的复振幅可表示为[1]

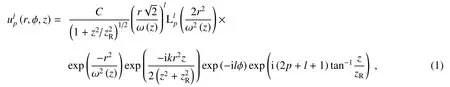
式中:C是常数;zR是瑞利距离;ω(z)是光束在z点的光斑半径;为拉盖尔多项式,p是径向指数,l是角向拓扑荷数;(2p+l+1)tan-1(z/zR)表示拉盖尔高斯模的Gouy相位。光束旋转相位在一个周期内从0到2π变化的次数就是光束的角向拓扑荷数。径向指数p+1表示光场环状同心圆数。简单起见,在这里只考虑p=0。图1为不同角向拓扑荷数的拉盖尔高斯模式光束的螺线相位结构图:当l>0时,光束呈现左旋现象;当l<0时,光束呈现右旋现象。

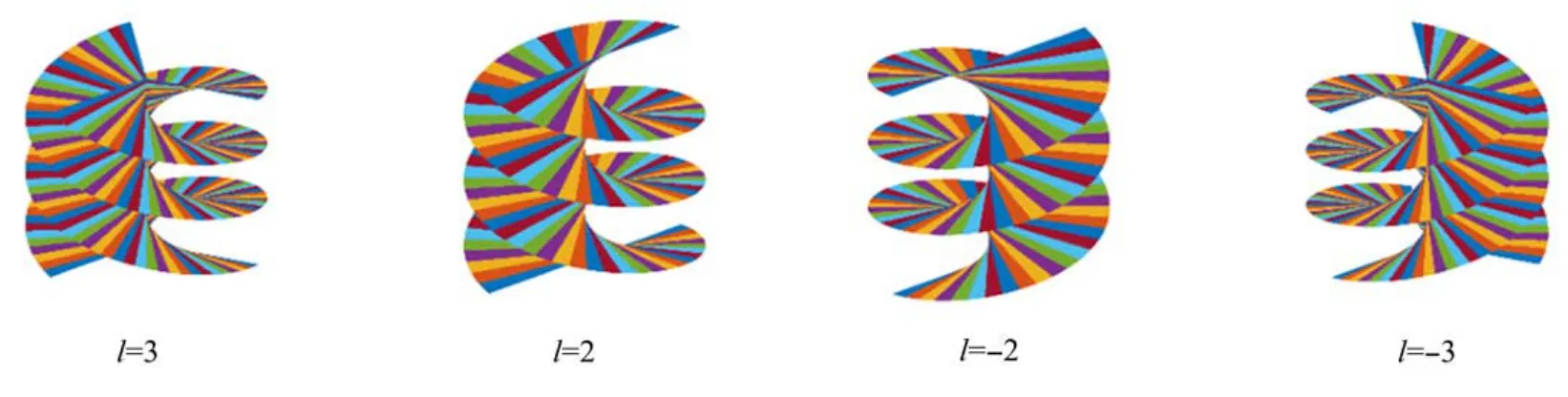
图1 p=0时拉盖尔高斯模式在不同角向拓扑荷数的螺旋相位波前[25]Fig.1 Helical phase wavefront of Laguerre-Gauss mode under different angular topological charges when p=0[25]

2 光学轨道角动量复用纠缠源的产生

2.1 光学轨道角动量复用的双光束纠缠源

在量子信息系统中,由于不同的光场模式代表不同的自由度,人们将这些模式集成在一个量子信息通道中,实现不同光场模式复用的纠缠,从而提高系统信息容量。基于这一思路,本研究小组用不同的轨道角动量模式代表不同的自由度,在连续变量体系中实现了光学轨道角动量模式复用的连续变量纠缠。

图2(a)为基于四波混频过程产生光学轨道角动量复用的双光束纠缠源的实验装置图,其中单个四波混频过程的能级结构如图2(b)所示。图2(a)中Rb cell为热铷原子蒸气池,P为泵浦光束,pr为探针光束,conj为共轭光束,LGl,pr和LG-l,conj为产生的两个不同模式的光,LO-l,pr和LOl,conj为探针光和共轭光的本地振荡光场。图2(c)为四波混频系统中的光学轨道角动量谱线,其中虚线所描述的对应关系表示该过程的轨道角动量守恒。图2(d)为利用道威棱镜实现本地振荡光模式从LO-l,pr到LOl,pr的转变。实验中一束强泵浦高斯光束P入射到热铷原子池中,经过四波混频过程后产生探针光场pr和共轭光场conj,且这两个光场中存在多对孪生光学轨道角动量模式,系统的总哈密顿量为

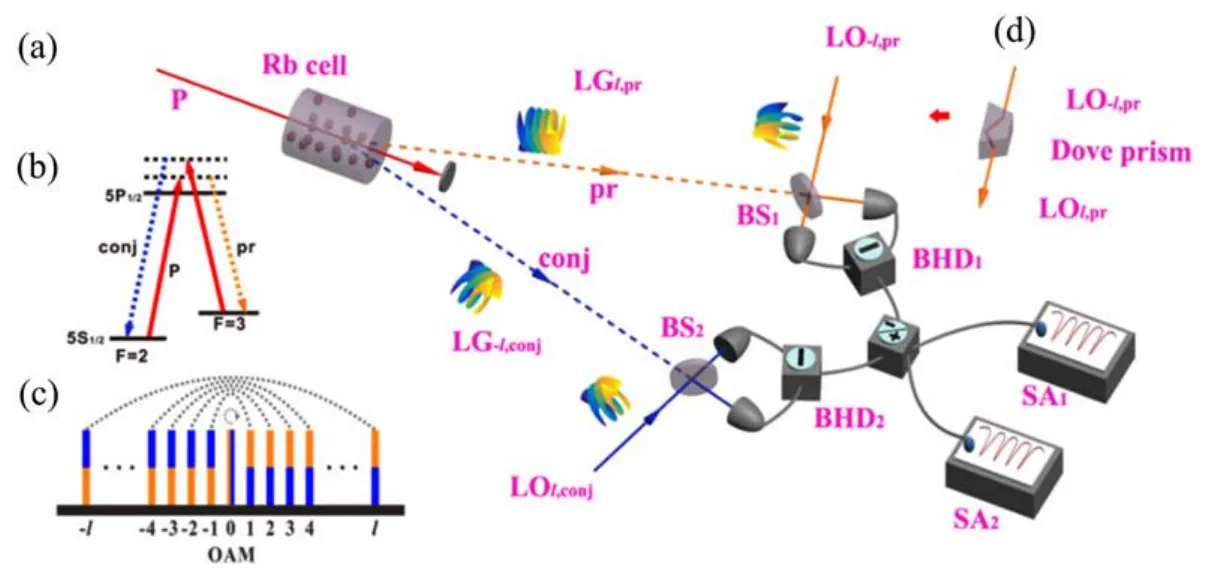
图2 (a)基于四波混频过程产生光学轨道角动量复用的双光束纠缠源方案;(b)85Rb D1线的双Λ能级结构;(c)四波混频系统中的光学轨道角动量谱线;(d)利用道威棱镜实现本地振荡光的模式转变[26]Fig.2 (a)Schematic experimental setup for generating the orbital-angular-momentum multiplexed bipartite entanglement source based on a four-wave mixing process;(b)The double-Λ energy level structure of85Rb D1 line;(c)The resultant orbital angular momentum spectrum from the four-wave mixing process;(d)A Dove prism is used to transfer the mode of local oscillator[26]

LGl,pr和LG-l,conj模式的纠缠特性随拓扑荷数l的变化关系如图3所示。图3中红色曲线A表示每对光学轨道角动量模式的增益强度,增益强度G=cosh2(γlt),其中t为四波混频过程的反应时间。蓝色曲线B表示其转置协方差矩阵的最小辛本征值ν,灰色阴影部分表示不同拓扑荷数对应的ν小于1。由图可见:|l|越大,G越小,这是因为光学轨道角动量模式的信号光的光斑大小会随|l|的增大而增大,导致其与泵浦光的重合部分减小,从而使非线性相互作用强度降低。另外,当|l|在[0,6]范围内,每对光学轨道角动量模式的转置协方差矩阵的ν都小于1,这表明它们是纠缠的。当|l|=7,8时,ν都大于1,说明相应的光学轨道角动量模式间没有纠缠。从蓝色曲线可以看出,当|l|=7,8时,G接近1,表明非线性相互作用强度很低,导致量子特性消失。从图3中还可以看出实验产生的光学轨道角动量模式复用数目为13。此外,LGl,pr和LG-l,conj模式存在纠缠意味着系统非线性相互作用满足轨道角动量守恒。

图3 LGl,pr和LG-l,conj模式的纠缠特性随拓扑荷数l的变化关系[26]Fig.3 The entanglement test between LGl,prand LG-l,conjmodes versus l[26]

为了更好地说明该系统的光学轨道角动量是守恒的,本课题组研究了l对LG-l,pr和LG-l,conj模式纠缠特性的影响。在实验中探针光场pr所对应的本地振荡光场上放置一个道威棱镜,其作用是实现本地振荡光场的模式从LO-l,pr到LOl,pr的转变。采用这种方法,可以通过产生的LOl,pr和LOl,conj模式的本地振荡光场来提取LG-l,pr和LG-l,conj模式的信息。实验结果如图4所示,其中红色曲线A和蓝色曲线B分别代表探针光场的增益强度G和转置协方差矩阵的最小辛本征值ν。由图可见:当l≠0时,ν都大于1,表明两个模式间不存在纠缠;此外,l越小,非线性相互作用强度越大,ν值越大,表明这两个模式之间的非关联性越大;而当l=0时,ν值小于1,这表明探针光场和共轭光场的两个高斯模式之间存在纠缠。以上结果一致表明四波混频过程非线性相互作用满足轨道角动量守恒。

图4 LG-l,pr和LG-l,conj模式的纠缠特性随拓扑荷数l的变化关系[26]Fig.4 The entanglement test between LG-l,prand LG-l,conjmodes versus l[26]

2.2 光学轨道角动量复用的三光束纠缠源

考虑到多体纠缠是实现量子网络和量子计算机所必须的资源,而利用轨道角动量可以增加纠缠的通道数,本课题组将轨道角动量复用的概念与多光纠缠的概念相结合,实现了光学轨道角动量复用的三光束纠缠源的制备。

图5(a)为基于级联四波混频过程产生光学轨道角动量复用的三光束纠缠源的实验装置示意图,其中单个四波混频过程的能级结构如图5(c)所示。图5(a)中Cell1和Cell2为热铷原子蒸气池,Pump1和Pump2为高斯泵浦光束,l,Pr0、-l,Conj0和-l,Conj0为注入真空场的湮灭算符,l,Pr2、-l,Conj1和-l,Conj2为产生的光学轨道角动量模式的湮灭算符,LGl,Pr2、LG-l,Conj1和LG-l,Conj2为产生的三束光Pr2、Conj1和Conj2对应的光学轨道角动量模式;图5(b)为利用道威棱镜实现本地振荡光模式转变。实验生成的三束光Pr2、Conj1和Conj2的输入输出关系为

图5 (a)基于级联四波混频过程产生光学轨道角动量复用的三光束纠缠源方案;(b)利用道威棱镜实现本地振荡光的模式转变;(c)85Rb D1线的双Λ能级结构[30]Fig.5 (a)Schematic experimental setup for generating the orbital-angular-momentum multiplexed tripartite entanglement source based on a cascaded four-wave mixing processes;(b)A Dove prism is used to transfer the mode of local oscillator;(c)The double-Λ energy level structure of85Rb D1 line[30]

为检测这些光学轨道角动量模式的纠缠,首先需要求它们的协方差矩阵。协方差矩阵可表述为,其中振幅和相位正交分量表示光学轨道角动量模式下的三光束的正交分量,不同的光学轨道角动量模式的三光束由不同的正交分量表示,其协方差矩阵也不同。利用协方差矩阵可以分析光场的纠缠特性,由于部分转置正定(PPT)判据能判断三光的所有1×2组合的不可分性质,因此使用PPT判据来判定三光纠缠是否存在。若所有组合部分转置协方差矩阵的PPT值均小于1,则可断定三光纠缠存在。

实验测量方法为通过三组平衡零拍探测获得光场的正交分量,再用频谱仪测量正交分量的方差,从而构建协方差矩阵,用PPT判据来分析三光之间的纠缠特性。图6(a)为不同光学轨道角动量模式的三光的PPT值随注入拉盖尔高斯光束拓扑荷数l的变化关系,以及不同光学轨道角动量模式下两个四波混频过程的增益变化趋势,其中曲线A和B分别对应级联四波混频过程的两个增益Gl,1和Gl,2,曲线C、D和E分别对应组合的PPT值。可以看出,两个四波混频过程的增益都随拓扑数绝对值|l|的增大而减小,这是因为随着|l|的增大,拉盖尔高斯光束的圆环直径增大,导致其与泵浦光重合度降低,非线性作用强度减弱。此外,在l从-4到4的范围内,三个组合的PPT值(对应曲线C,D,E)都小于1,表明系统中同时存在9组光学轨道角动量复用的三光纠缠,其示意图如图6(c)所示。而当|l|大于4时,三个组合的PPT值出现了大于1的情况,表明三光之间没有纠缠,这是由于随着|l|的增大,四波混频过程反应强度逐渐降低,从而导致量子关联性逐渐消失。此外,还计算了三光束间两两光束组合的PPT值,如图6(b)所示,其中曲线F、G和H分别对应LG-l,Conj1|LG-l,Conj2、LGl,Pr2|LG-l,Conj1和LGl,Pr2|LG-l,Conj2组合的PPT值。可以发现当l从-4到4变化时,LGl,Pr2|LG-l,Conj1组合的PPT值均小于1;当l从-5到5变化时,LGl,Pr2|LG-l,Conj2组合的PPT值均小于1,表明该组合中的两个模式是纠缠的。而LG-l,Conj1|LG-l,Conj2组合无论在l等于多少时都有PPT值大于1,表明该组合的两个模式间不存在纠缠,这是因为这两个模式的光束之间不存在关联。实验结果表明:该级联四波混频系统确定性地产生了9组光学轨道角动量复用的三光纠缠,也同时存在9组LGl,Pr2|LG-l,Conj1之间的两光纠缠以及11组LGl,Pr2|LG-l,Conj2之间的两光纠缠,如图6(d)所示。以上结果也表明四波混频过程产生的光学轨道角动量模式是成对产生的,满足轨道角动量守恒。

图6 (a)对LGl,Pr2、LG-l,Conj1和LG-l,Conj2模式间三光纠缠的验证;(b)对LGl,Pr2、LG-l,Conj1和LG-l,Conj2模式间任意两种组合的两光纠缠的验证;(c)光学轨道角动量复用的三光纠缠的概念图;(d)光学轨道角动量复用的两光纠缠的概念图[30]Fig.6 (a)The test of tripartite entanglement among LGl,Pr2,LG-l,Conj1and LG-l,Conj2modes;(b)The test of bipartite entanglement between any two of LGl,Pr2,LG-l,Conj1and LG-l,Conj2;(c)Diagram of orbital-angular-momentum multiplexed tripartite entanglement;(d)Diagram of orbital-angular-momentum multiplexed bipartite entanglement[30]

2.3 光学轨道角动量复用的六光束纠缠源

多组份纠缠是构建量子网络的基本要素,其规模决定了它携带和处理量子信息的能力。如果能够同时存在独立的、正交的多通道多组份量子纠缠,那么量子网络的信息容量将大大提高[25]。连续变量纠缠可以确定性地产生,因此可以通过增加纠缠模数或多路复用通道来提高连续变量系统纠缠的规模。同时,为了实现长距离、大容量的量子通信,需要空间上模式分离的大规模纠缠。本课题组基于四波混频过程产生空间分离的多组份纠缠,并利用光学轨道角动量复用增加纠缠通道的数量,从而大大增加多组份纠缠的规模。

图7为产生大规模多组份量子纠缠的方案原理图,其中BE、HE和ME分别表示两组份纠缠、六组份纠缠和多组份纠缠,SPS表示泵浦整形技术,OAM为光学轨道角动量。通过七个并发的四波混频过程可以确定性地产生连续变量六组份纠缠。为了大大增加纠缠的规模,利用光学轨道角动量复用的概念,六组份纠缠的每个节点都有11种可以单独访问且相互正交的光学轨道角动量模式[25]。因此,可以通过在66个轨道角动量模式上同时生成11个六组份纠缠来确定性地生成大规模量子网络。

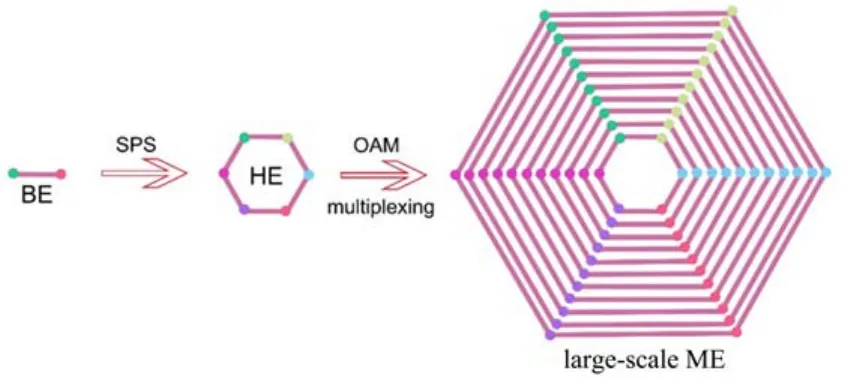
图7 产生大规模多组份量子纠缠的方案原理图[31]Fig.7 The principle for engineering large-scale multipartite entanglement[31]

实验方案如图8(a)所示,钛宝石激光器产生的两个泵浦光束Pump1和Pump2在铷原子蒸气池的中心交叉。将部分泵浦光通过声光调制器以产生弱高斯探针光束Probe(5)。接着让高斯探针光束通过空间光调制器来生成不同拓扑电荷数l的拉盖尔高斯光束。图8(b)为六个拉盖尔高斯光束相互作用的结构示意图,七个并发的四波混频过程在同一个铷原子蒸气池中发生,每一个四波混频过程都遵循图8(c)所示的能级结构图。

首先,探针光束可以通过单泵浦四波混频过程与每个泵浦光相互作用。探针光束被放大的同时产生两个共轭光束(1和3)。除了单泵浦的情况,探针光束在满足相位匹配的条件下还可以与两个泵浦光束同时相互作用,在这种双泵浦的情况下,每个泵浦光束会湮灭一个光子,探针光束会获得一个光子,同时另一个光子会在新的共轭光束(2)中产生。新的探针光束4(6)是由光束2和Pump1(Pump2)之间的单泵浦相互作用或光束3(1)与两个泵浦光之间的相互作用产生的。因此,整个过程表现为探针光束Probe(5)被放大的同时产生两个新的探针光束(4和6)和三个共轭光束(1、2和3)。由于光束5是携带光学轨道角动量的拉盖尔高斯光束,所以六个输出光束也携带光学轨道角动量。由于轨道角动量守恒,输出的探针光束和共轭光束的拓扑电荷数相反,因此改变探针光束Probe(5)的拓扑电荷数l就可以得到多个携带不同光学轨道角动量模式的六组份纠缠通道。由于这六组份纠缠的不同通道之间彼此正交,因此可以单独访问六组份纠缠的每个通道。当注入拓扑电荷数为5的光学轨道角动量模式的探针光束时,相机捕获六个输出光束的强度模式如图8(d)所示。为了显示六个输出光束的相互作用结构,往这七个并发的四波混频过程注入明亮的探针光束Probe(5),但是当证明纠缠时,把注入的探针光束Probe(5)挡住,从而使测量的过程纯粹是自发的。

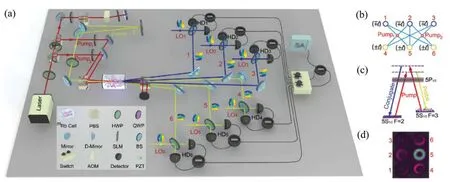
图8 (a)基于七个并发的四波混频过程产生光学轨道角动量复用的六光束纠缠源的实验方案;(b)六个拉盖尔高斯光束的相互作用结构;(c)85Rb D1线的双Λ能级结构;(d)当注入的探针光束5的拓扑电荷数为5时对应输出光场的捕获图像[31]Fig.8 (a)Schematic experimental setup for generating the orbital-angular-momentum multiplexed hexapartite entanglement source based on seven concurrent four-wave mixing processes;(b)Interaction structure of the six LG Beams;(c)The double-Λ energy level structure of85Rb D1 line;(d)The camera-captured intensity pattern of six orbital angular momentum modes when the topological charge of the injected probe beam 5 is 5[31]

为了证明一个通道内六个光学轨道角动量模式是纠缠的,利用带有本地振荡光的平衡零拍探测技术来提取光束中特定的光学轨道角动量模式。本地振荡光经过平衡零拍探测可以得到六个信号光场的正交振幅和正交相位的涨落,在这里,通过六个独立的平衡零拍探测来获得六组份纠缠的每个通道完整的协方差矩阵。将测得的协方差矩阵进行部分转置处理得到部分转置协方差矩阵,利用PPT判据来判断输出光场是否为纠缠态。对于六组份而言,存在三种可能的转置类型:1×5,2×4和3×3,共有31种组合方式。若所有组合部分转置协方差矩阵的最小辛本征值均小于1,则表示存在六组份光学轨道角动量模式纠缠,且辛本征值越小纠缠越强[32]。

为了验证六组份纠缠的纠缠特性,将注入光束的拓扑电荷数l的变化范围设置为-5到5,图9(a)和图9(b)为拓扑电荷数l在-5到5范围内时所有31种组合的辛本征值。可以看出,对于每一个l,所有31种组合的辛本征值均小于1,这表明实验确定性地产生了11个光学轨道角动量复用的六组份纠缠。图9(c)和图9(d)为有探针光束5注入时,计算机生成的全息图加载在空间光调制器上生成的六个光学轨道角动量模式相应的强度分布图。可以看出,在每一种情况下,生成的六个光学轨道角动量模式的光束大小都相同,这是因为|l|相等。

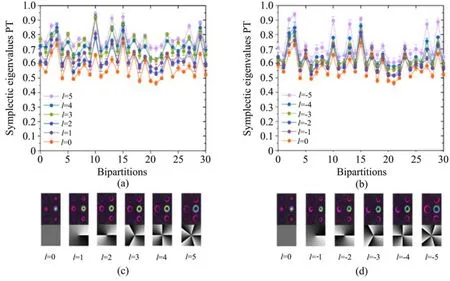
图9 (a),(b)不同拓扑电荷数l(-5≤l≤5,l为整数)的情况下所有组合的31个辛本征值;(c),(d)六个拉盖尔高斯光束的强度和相位分布图[31]Fig.9 (a),(b)All 31 symplectic eigenvalues under different cases of the topological charge l(-5 ≤ l≤ 5,l is an integer);(c),(d)The intensity and phase patterns of the six Laguerre-Gauss beams[31]

3 光学轨道角动量复用纠缠源的应用

3.1 光学轨道角动量复用的全光量子隐形传态

量子隐形传态是量子信息中重要的协议之一[33-39]。除了增加远程传输的规模外,提高其信息传输能力对其实际应用也至关重要。利用基于四波混频过程的光学轨道角动量多路复用连续变量纠缠和光学轨道角动量模式匹配参量放大器,本课题组在实验中建立了9通道并行全光量子隐形传态。

利用光学轨道角动量复用进行并行全光量子隐形传态的实验装置如图10(a)所示。其中Alice、Bob和Victor分别代表全光量子隐形传态的发送方、接收方和验证方,Alice和Bob通过一个全光学通道相连,in为输入相干态,out为输出态,EPR state为爱因斯坦-波多尔斯基-罗森纠缠源。Alice在EPR2的帮助下,通过光学轨道角动量模式匹配的参量放大器放大了携带光学轨道角动量模式的输入态。将in的强度增益设置为10以确保放大后的in可视为经典场。Alice通过全光经典通道将放大后的信号发送给Bob,为了重构输入态in,Bob接收方通过偏振分束器耦合放大后的in和EPR1。在EPR1的路径中放置一个压电陶瓷(PZT)用来改变EPR1和EPR2之间的相对相位。然后,Victor通过平衡零拍探测测量输出态out的正交振幅(相位)噪声,并计算其传输保真度F。平衡零拍探测技术利用本地振荡光来提取输出态的光学轨道角动量模式。out的路径中放置了另一个PZT,用来改变信号光和本地振荡光之间的相对相位。

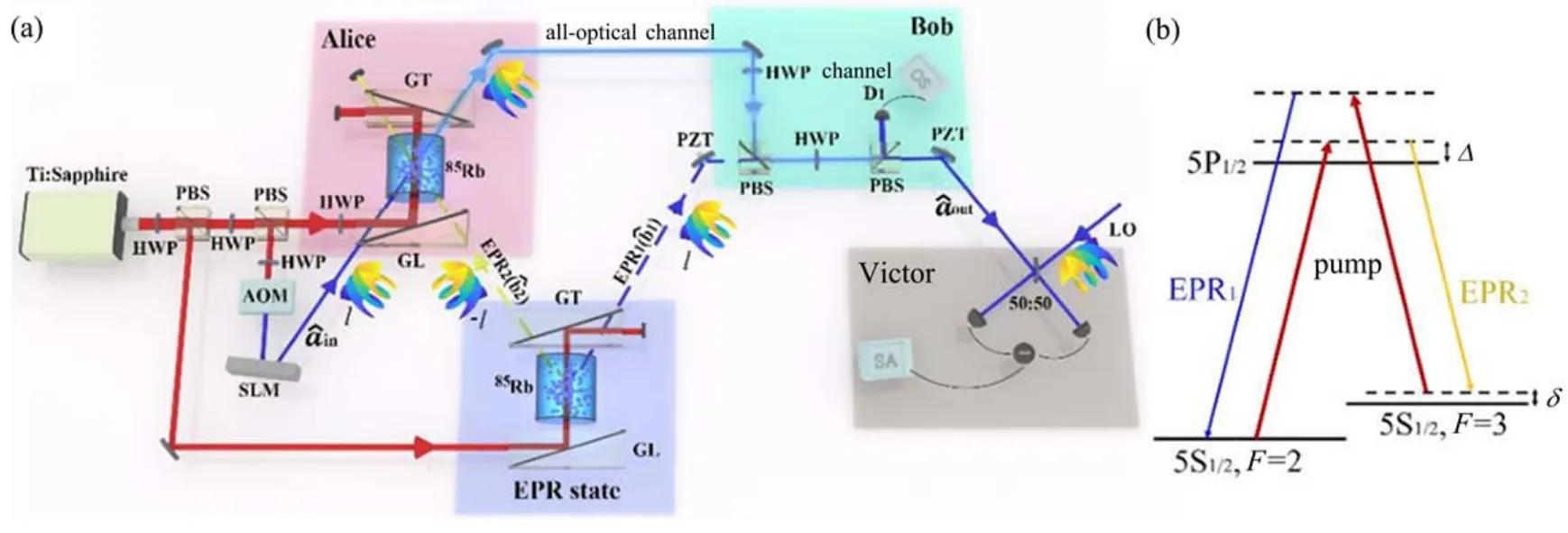
图10 (a)并行全光量子隐形传态的实验装置图;(b)85Rb D1线的双Λ能级结构[40]Fig.10 (a)Experimental setup for parallel all-optical teleportation;(b)The double-Λ energy level structure of85Rb D1 line[40]

图11(a)、(b)为Victor验证方用平衡零拍探测测得的l=1光学轨道角动量模式输出态的正交振幅和相位的噪声。如图11(c)、(d)所示,EPR纠缠的正交振幅差(正交相位和)的噪声为(2.51±0.16)dB[(2.58±0.18)dB],蓝色曲线的最低噪声低于相应的散粒噪声极限(黑色线),这表明在这两种光学轨道角动量模式之间存在纠缠。遮挡住纠缠源和光学轨道角动量模式匹配的参量放大器的泵浦光束后,测得的正交振幅和相位的噪声由图11(a)、(b)中的黑色线表示。为了实现全光量子隐形传态,需要将纠缠分发给Alice和Bob,并通过扫描PZT来改变EPR1和EPR2之间的相对相位。图11(a)和图11(b)中的红色曲线分别表示在Victor处测得的输出态的正交振幅和正交相位的噪声功率谱线。其中红色曲线的最小值表示EPR1和EPR2之间的相对相位,对应于。因此可以将每个曲线的最小值表示为输出态正交振幅(相位)out(out)的噪声。out和out的噪声几乎相等,并且比输入态的相应正交分量的噪声高(3.58±0.21)dB,这表明在EPR纠缠态的帮助下,通过量子隐形传态重构的态的保真度为0.61±0.02。为了与相应的经典全光隐形传态进行比较,通过挡住纠缠源测得的正交振幅(相位)噪声由图11(a)、(b)中的蓝色线表示,它们比相应输入态的正交振幅(相位)噪声高(4.66±0.12)dB。而相应的经典全光隐形传态的保真度为0.51±0.01,这表明此全光量子隐形传态保真度突破了经典极限。然后对输出态进行了光学轨道角动量模式分析,结果如图11(e)所示,输出态和输入态的光学轨道角动量模式完全一致。以上结果表明本课题组成功实现光学轨道角动量模式l=1的相干态的量子隐形传态。

图11 (a),(b)输出态的正交振幅(相位)的噪声;(c),(d)光学轨道角动量复用纠缠的正交振幅(相位)测量;(e)光学轨道角动量模式分析的结果,l=1情况下计算机生成的全息图以及相应的输入和输出光场图像分别显示在右边插图中[40]Fig.11 (a),(b)The variance of amplitude(phase)quadrature of the retrieved state;(c),(d)The amplitude(phase)quadrature measurement of the orbital-angular-momentum multiplexed entanglement;(e)The results of orbital angular momentum mode analysis,the computer-generated hologram for l=1 case and the corresponding images of input and output fields are shown on the right inset,respectively[40]

为了证明光学轨道角动量多路复用的全光量子隐形传态可以提高通道容量,令输入态携带的拓扑荷数在-5到5之间变化,保持放大增益为10不变,进行上述一系列测量。全光量子隐形传态的保真度随拓扑荷数的变化关系(红色线)和经典全光隐形传态的保真度(蓝色线)如图12(a)所示。结果表明,通过全光量子隐形传态传输拓扑荷数为-4到4的相干态的保真度优于相应的经典隐形传态的保真度。然后通过压缩判据计算了光学轨道角动量复用纠缠的纠缠度,该判据直接关联纠缠的压缩度[41,42]。结果如图12(b)所示,其中蓝色线表示光学轨道角动量复用纠缠的纠缠度随拓扑荷数l的变化关系,黑色线表示纠缠度的上限。以上测量结果表明本课题组成功构建了9个不同光学轨道角动量模式复用的全光量子隐形传态并行通道。

图12 (a)用于传送不同光学轨道角动量模式的全光隐形传态(AOT)的保真度;(b)光学轨道角动量复用纠缠的纠缠度随拓扑荷数l的变化[40]Fig.12 (a)The fidelity of all-optical teleportation(AOT)for teleporting different orbital angular momentum modes;(b)The inseparability of the orbital-angular-momentum multiplexed entanglement versus topological charge l[40]

3.2 光学轨道角动量复用的量子密集编码

量子密集编码是量子信息的一种基本协议[43-49],量子密集编码方案可以用于提高通道容量。在连续变量系统中,使用多路纠缠源来突破传统量子密集编码方案的通道容量是很有希望的。由于光学轨道角动量[50-54]已经被用于实现多路复用,因此本课题组利用光学轨道角动量来实现光学轨道角动量复用的量子密集编码,从而提高量子密集编码方案的通道容量。利用光学轨道角动量复用进行量子密集编码的实验装置如图13(a)所示,Pr表示探针光束,Conj表示共轭光束,LO表示本地振荡光。在热85Rb原子池中发生四波混频过程的能级结构如图13(b)所示,其中Δ为单光子失谐,δ为双光子失谐。实验中,偏振分束器将激光分成两部分,功率较强的一束作为泵浦光束,另一束弱光通过声光调制器以产生注入的探针光束。然后,探针光束通过空间光调制器被编码在拉盖尔高斯(LG)模式上(LGl模式或LGl+LG-l叠加模式)。编码在拉盖尔高斯模式下的探针光束和泵浦光束以一定的夹角交叉入射到热铷原子蒸气池中,经过四波混频反应从而产生爱因斯坦-波多尔斯基-罗森(EPR)纠缠源。接着,将探针光束(EPR1)被分发给Alice,Alice通过振幅调制器和相位调制器分别将经典振幅信息和相位信息编码到探针光束上。在Bob接收方,信号在另一个EPR光束(共轭光束EPR2)的帮助下通过两个平衡零拍探测被解码。让两个平衡零拍探测获得的两个光电流经过一个混合接头,通过两个频谱分析仪分析混合接头的输出信号。当四波混频过程的泵浦光束被阻挡时,上述过程可以视为带有LGl或LGl+LG-l叠加模式的相干态方案,将这些相干态方案视为传统量子密集编码或光学轨道角动量复用量子密集编码的经典对应物。

图13 (a)光学轨道角动量复用的量子密集编码的实验方案;(b)85Rb D1线的双Λ能级结构[55]Fig.13 (a)Experimental setup for orbital-angular-momentum multiplexed quantum dense coding;(b)The double-Λ energy level structure of85Rb D1 line[55]

为了证明所提出方案可以提高通道容量,首先从理论上介绍一下通道容量。一般来说,以高斯概率分布的量子态的通道容量可以表示为[56]

式中:S为信号功率,N为噪声功率,S/N即为信噪比(SNR)。为了公平地比较不同方案的通道容量,通道中每带宽每秒的平均光子数¯n必须是固定的。而当调制信号的功率满足大功率调制的条件时,平均光子数只与调制信号的功率有关。因此可以将调制信号的功率固定为VS并保持不变以使不同方案的平均光子数保持不变。从平衡零拍探测测得的噪声功率谱中得到四种方案(编码于LGl模式的相干态方案,编码于LGl+LG-l叠加模式的相干态方案,传统量子密集编码方案和光学轨道角动量复用的量子密集编码方案)的信噪比。

利用测得的信噪比可以给出相应方案的通道容量,四种不同方案的通道容量如图14所示,其中误差由多次重复测量的标准差得到。图中橙色柱状表示编码于LGl模式(l=-2,-1,0,1,2)的相干态方案的通道容量,灰色柱状表示编码于LGl+LG-l叠加模式(l=1,2)的相干态方案的通道容量,蓝色柱状表示编码于LGl模式(l=-2,-1,0,1,2)的注入探针光束的传统量子密集编码方案的通道容量,深紫色柱状表示编码于LGl+LG-l叠加模式(l=1,2)的注入探针光束的光学轨道角动量复用量子密集编码方案的通道容量。可以看出,在EPR纠缠源的帮助下,传统量子密集编码方案(蓝色柱状)的通道容量超越了经典对应的相干态方案(橙色柱状)的通道容量,并且在l=0的情况下,通道容量有0.4 dB的增强。更重要的是,当注入探针光束编码在LGl+LG-l模式上时,光学轨道角动量复用量子密集编码方案(深紫色柱状)的通道容量显著提高,与相应的传统量子密集编码方案(蓝色柱状)相比提高了2.4 dB。这表明光学轨道角动量复用量子密集编码方案在通道容量上可以超越相应的传统量子密集编码方案。此外,光学轨道角动量复用量子密集编码方案(深紫色柱状)与经典对应的相干态方案(橙色柱状)相比,实现了2.7 dB通道容量的提高。在连续变量和离散变量系统中,传统的量子密集编码很难达到提升3 dB通道容量的水平。为了实现通道容量的倍增,在传统离散变量量子密集编码中所有的四种贝尔态都需要被确定地区分开来[57,58],在传统连续变量量子密集编码中[59]则需要产生超高水平的压缩,而这两者都是极难实现的。综上所述,本课题组的结果明确表明了光学轨道角动量复用的量子密集编码在大幅提高通道容量方面具有巨大的优势。

图14 不同方案及不同拓扑荷数下的通道容量[55]Fig.14 The channel capacities for different schemes versus topological charges l[55]

4 结论

介绍了光学轨道角动量的基本概念,综述了在连续变量系统中基于四波混频过程的光学轨道角动量复用的两光[26]以及三光[30]纠缠源的制备。将经典通讯系统中复用的概念应用到连续变量量子系统中,实现了光学轨道角动量复用的连续变量纠缠,有效地提高了连续变量量子系统的通道容量。为了进一步增大纠缠的通道数量,还构建了基于66个光学轨道角动量模式的大规模量子网络[31],为高效构造大规模光量子网络提供了一种新的思路。此外,还利用光学轨道角动量复用的连续变量纠缠成功构建了9个全光量子隐形传态的并行通道[40],实现了光学轨道角动量复用的量子密集编码方案[55],使得其通道容量相比于传统量子密集编码方案有大幅提高。在现有工作的基础上,下一步将继续寻找更有效的方法和手段来大幅增加光学轨道角动量模式复用数目,进一步扩大量子网络的规模和增大量子信息协议的通道容量。