光的自旋-轨道相互作用

许文昊,寿一畅,罗海陆

(湖南大学物理与微电子科学学院自旋光子学实验室,湖南 长沙 410082)

0 引言

自旋-轨道相互作用这一术语起源于量子物理学,用于描述电子或其他量子粒子自旋角动量和轨道角动量之间的耦合[1]。电子的自旋-轨道相互作用通常被解释为电子的运动磁矩与外部电场的耦合,此外,自旋-轨道相互作用的几何相描述揭示了它本质上与粒子的角动量有关[2]。尽管自旋-轨道相互作用在不同系统中具有不同的表现形式,但其统一特征表现为粒子的自旋和动量之间的耦合。电子的自旋-轨道相互作用有两种基本的表现形式:首先,自旋-轨道相互作用使得电子在磁场中运动时能级发生精细分裂[3,4];其次,由于自旋-轨道相互作用,电子在外场中运动时会发生与自旋相关的横向偏转,即电子自旋霍尔效应[5-7]。由于经典光或量子光子也同时拥有自旋角动量和轨道角动量,在某些条件下,光的自旋角动量和轨道角动量之间也会发生耦合,这就是光的自旋-轨道相互作用[8]。

在20世纪90年代,Zel’dovich研究组首次提出光的自旋-轨道相互作用的概念[9]。在一系列开创性工作中,他们研究了在透镜、非均匀介质、多模光纤中和自旋相关的效应[10-13]。早在50年代,和自旋相关的光学现象就已经引起科学家的重视。1955年,Fedorov[14]在理论上预言,当光束在玻璃-空气界面发生全内反射后,光束重心会发生垂直入射面的横向位移。一般情况下,这种位移非常小,实验很难观测。1972年,Imbert[15]将光在棱镜中多次反射放大这种效应,在实验中首次观察到这种位移。因此,后来这种光在光学界面反射或折射产生的与自旋相关的位移被统称为Imbert-Fedorov位移。当时,关于亚波长下自旋-轨道相互作用的理论解释存在争议,仅有的实验结果并不能支撑理论解释。直到2004年,贝里几何相位和光的角动量的引入使得光的自旋-轨道相互作用物理图像更加清晰[16,17]。此外,随着测量技术的进步,例如量子弱测量技术的引入[18],光的自旋-轨道相互作用得到精确测量。因此,光的自旋-轨道相互作用的相关研究取得了重要进展[19]。

近年来,人们对光的自旋-轨道相互作用产生了浓厚的兴趣,它既具有基础理论意义又具有应用价值。一方面,光的自旋-轨道相互作用具有重要的物理意义,因为它揭示了自旋为ħ的粒子演化过程中普遍存在的几何动力学特性。通过这种方式,从经典光学的角度就可以直接观测到在高能物理和凝聚态物理中无法观测到的微小效应。另一方面,尽管在传统的宏观几何光学中可以安全地忽略波长尺度的自旋-轨道相互作用,但在亚波长尺度下,像传播、反射、折射、聚焦、散射、衍射等基本光学过程都会受到自旋-轨道相互作用的影响。因此,光的自旋-轨道相互作用具有重要的理论和实际价值。在纳米光学、光子学、量子光学等领域占据极其重要的地位,并在精密探测、光场调控、光学模拟运算、显微成像、量子成像等方面具有重要的应用前景。本文旨在对光学系统中的自旋-轨道相互作用现象给出一个统一的描述,并从光子角动量和几何相位两方面揭示其物理起源,介绍自旋-轨道相互作用研究进展,最后对其可能发展的研究方向进行展望。

1 光的角动量与几何相位

光的角动量与几何相位是用来描述光的自旋-轨道相互作用的两个重要物理量。这两个物理量的引入使光的自旋-轨道相互作用的物理图像更为清晰。

1.1 光的角动量

众所周知,光具有波粒二象性,因此光子和经典粒子一样具备自旋角动量和轨道角动量,与电子等粒子不同的是这些角动量能够影响光的偏振和相位。1909年,英国物理学家Poynting[20]就指出,光子的自旋角动量与光的偏振态有关。1936年,Beth[21]验证了左、右旋圆偏振光子分别携带有自旋角动量

光子自旋角动量S与光束传播方向一致(动量p=〈k〉),取决于圆偏振度σ,其中σ=±1分别对应左旋和右旋圆偏振(图1)。在量子力学图像中,随着电场和磁场围绕波矢量方向旋转,左右圆偏振与光子的两个自旋态相对应,左右旋圆偏振光子分别携带+ħ和-ħ的自旋角动量,其中ħ是简化的普朗克常数。

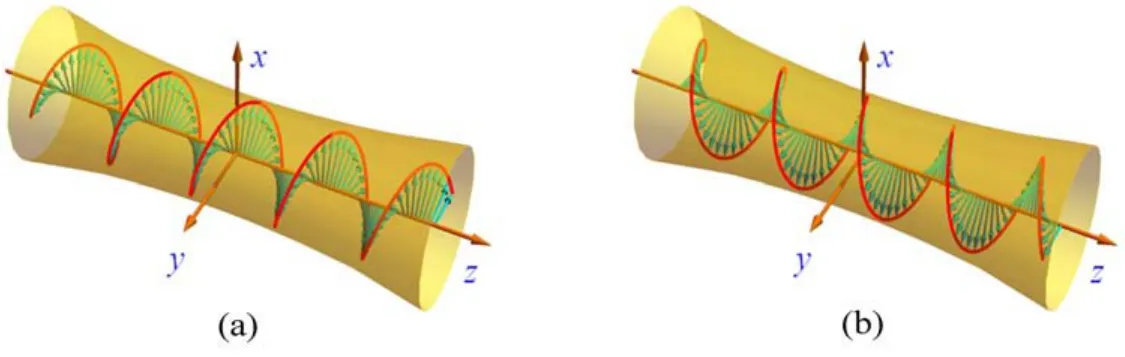
图1 傍轴光束的自旋角动量。(a)携带自旋角动量为S=+ħ的圆偏振光瞬时电场矢量;(b)携带自旋角动量为S=-ħ的圆偏振光瞬时电场矢量Fig.1 Spin angular momenta of paraxial optical beams.(a)Left-hand circularly polarized beam with S=+ħ;(b)Right-hand circularly polarized beam with S=-ħ

1992年,荷兰科学家Allen等[22]发现了光子还具有轨道角动量。此后,以光学角动量为基础的众多应用迅速成为光学研究前沿,在粒子操控、图像处理、显微成像、量子成像等方面得到了广泛的研究和应用[23]。这种光的轨道角动量与光场空间分布的坐标选取无关,仅与螺旋相位波前有关,因此也被称为内禀轨道角动量(图2)。内禀轨道角动量可以写为

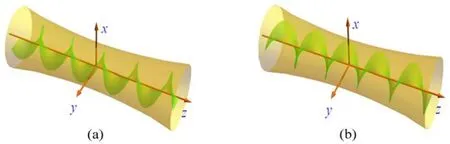
图2 傍轴涡旋光束的内禀轨道角动量。(a)l=+1;(b)l=-1Fig.2 Intrinsic orbit angular momenta of paraxial vortex beams.(a)l=+1;(b)l=-1

这种具有涡旋相位eilφ的光束中每个光子都携带lħ的轨道角动量,其中φ表示方位角,l为整数,表示轨道角动量量子数,也称拓扑荷数。

光的外禀轨道角动量和坐标原点的选取有关,与粒子轨道角动量类似,它等于光束重心的位置矢量与动量P的叉乘,即

因此,光的外禀角动量与光束重心偏移量、传播路径有关(图3)[19]。一般情况下,螺旋相位体现为旋转对称结构,因此这种光束具有内禀的轨道角动量。但如果打破其旋转对称性,会使光束重心偏移,从而导致内禀轨道角动量转换为外禀轨道角动量。此外,外禀轨道角动量也出现在各种光束位移中。

图3 傍轴光束的外禀轨道角动量。(a)光束相对于坐标原点发生y方向正的位移,产生x方向正的外禀轨道角动量;(b)光束相对于坐标原点发生y方向负的位移,产生x方向负的外禀轨道角动量Fig.3 Extrinsic orbit angular momenta of paraxial optical beams.(a)The beam undergoes a positive displacement in y direction,resulting in a positive extrinsic orbital angular momentum in x direction;(b)The beam undergoes a negative displacement in y direction,resulting in a negative extrinsic orbital angular momentum in x direction

1.2 几何相位

当一矢量在三维曲面沿一闭合路径做平行移动一周,矢量回到起点,矢量的方向和出发时相比旋转了一定角度,这种现象为矢量方向的整体改变。在曲面上平行运动,要求矢量相对于曲面的法线没有发生转动。当矢量从一点平行移动到相邻点,其相对于两相邻点形成的切平面没有转动,即在平行移动时矢量没有发生局域改变。因此,这种无局域改变却有整体改变的现象实际就是三维曲面上的几何现象,整体改变和几何路径有关。如果矢量在平直空间沿一闭合途径平行移动一周,矢量回到起点时则不会发生旋转。前面提到的三维局面,不局限于位置空间或动量空间的现实曲面,也可以是参数空间的曲面。光学系统中有两种常见的弯曲空间:动量空间和斯托克斯参数空间,可以分别用来描述两类几何相位,即自旋重定向贝里相(Spin-redirection Berry phase)和潘查拉特南-贝里相(Pancharatnam-Berry phase)。

当光在光学界面反射或波导中传播时,其传播方向发生改变,实际上就是波矢在动量空间的球面上平行移动[图4(a)]。平面波的偏振方向总是垂直于波矢方向(即k),意味着偏振方向取决于波矢方向,并且与波矢空间的球面相切。偏振矢量在局域上不发生转动,但整体上发生转动。这是一种几何效应,必然诱导与圆偏振光相关的几何相位。在实验室坐标系下,将圆偏振光场Eσ转换到用(θ,φ)表示的球坐标系,然后几何相位就可以用对应的贝里联络(Berry connection)Aσ(k)和贝里曲率(Berry curvature)Fσ(k)来表示[24]

图4 三维曲面空间中矢量平行移动产生几何相。(a)波矢在动量空间中的闭合路径作非平庸的平行移动;(b)斯托克斯矢量在球面上的非平庸的平行移动Fig.4 Geometric phase in three-dimensional curved space.(a)The non-trivial parallel transport of the wave vector along a closed path in three-dimensional momentum space;(b)The non-trivial parallel transport of Stokes vector in three-dimensional Stokes space

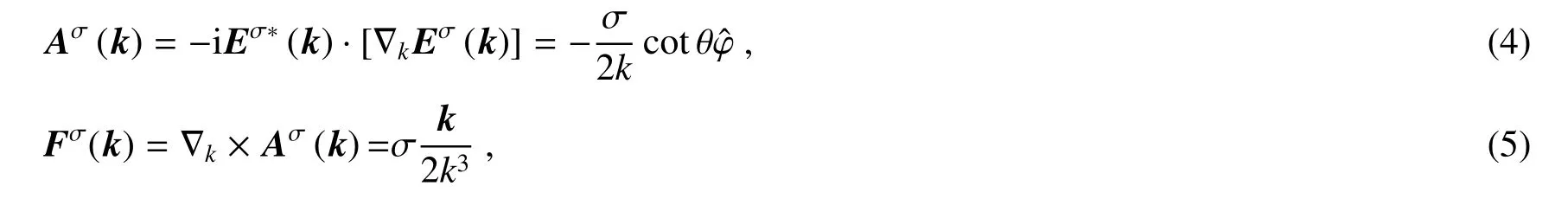
其中贝里联络和贝里曲率在动量空间中分别扮演有效的“矢量势”和“磁场”。在贝里的理论框架中,偏振Eσ(k)在参数空间中的闭合路径C进行平行移动,然后返回到初始态,获得额外的几何相位

对于确定入射角θ决定的入射面,左右旋圆偏振会获得相反的几何相ΦG=-σφcosθ。对于整个环路,减去在球坐标中旋转的2π,因此闭合路径在波矢空间球面上围成的立体角Ω所对应的全局几何相位可以写成

另外一种弯曲空间是斯托克斯(Stokes)球,用来描述偏振态在斯托克斯参数空间的演化。矢量在球面上的平行移动揭示了传输矢量与坐标系之间不可避免的旋转,因此必然诱导圆偏振光的几何相位[图4(b)]。偏振态ψ(R)在斯托克斯参数空间演化,几何相位就可以用对应的贝里联络Aσ(R)和贝里曲率Fσ(R)表示为[19]

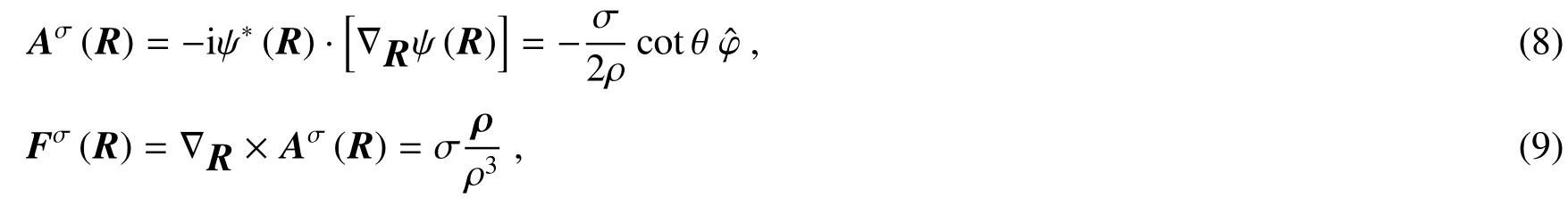
其中,贝里联络和贝里曲率在动量空间中分别扮演有效的“矢量势”和“磁场”。在贝里的理论框架中,状态ψ(R)沿着参数空间中闭合路径进行平行移动,经历一个循环后返回到初始态,获得额外的几何相位

在球坐标中 dS= σρ2sinθdρdφdθ,几何相可以写成

因此,无论是在动量空间还是在斯托克斯参数空间,贝里联络和贝里曲率有类似的表达形式,几何相位均可以简单地表示为立体角的二分之一。

这里讨论的两种情况都是矢量在弯曲空间中的闭合路径平行移动,目的是为了更加方便地分析几何相,因为几何相等于闭合路径包含面积所对应的立体角的二分之一。实际上,矢量在弯曲空间中平行移动大多都不是闭合路径,例如光在界面反射、折射、聚焦或光被微小粒子散射。这些行为如用动量空间来表述,波矢在动量空间中的演化路径是不闭合的。这种情况可以通过波矢在动量空间平行移动导致的偏振态整体旋转来分析几何相。理解几何相的关键是偏振态没有局域改变,但发生了整体改变,这也是矢量在曲面上演化导致的现象。

2 光的自旋-轨道相互作用

光的自旋角动量可以分别与内禀轨道角动量或外禀轨道角动量发生相互作用。因此,光的自旋-轨道相互作用可以分为两种:自旋-内禀轨道角动量相互作用和自旋-外禀轨道角动量相互作用。

2.1 光的自旋-内禀轨道角动量相互作用

自旋角动量和内禀轨道角动量之间的相互作用通常发生在圆柱形或球形对称系统中,主要表现为聚焦或者散射光场中自旋相关的效应和各向异性结构诱导的现象。以聚焦或散射场中自旋相关效应和各向异性结构诱导的自旋-轨道相互作用为例,对自旋角动量和内禀轨道角动量相互作用进行具体阐释。这两者中聚焦和散射属于“内”效应,源于光束的非傍轴性,这种行为能够直接用麦克斯韦方程组描述,很典型的一个例子就是非傍轴光束被高数值孔径透镜聚焦或者被微小粒子散射,此时,自旋-轨道相互作用会强烈地影响光场的分布[25-29]。

考虑一个聚焦的圆偏振光束携带自旋角动量,圆偏振平面波矢在方位角θ处形成一个圆锥形分布,自旋角动量和内禀轨道角动量的表达式可以写为[30]

可以明显看出部分自旋角动量转化为内禀的轨道角动量,但光束总角动量守恒,Jz=Sz+Lz=σ。这是光的自旋-轨道相互作用的典型物理现象:自旋角动量向轨道角动量转化,即自旋角动量和内禀轨道角动量的相互作用。当方位角θ=π/2时,所有的自旋角动量都转化为内禀的轨道角动量。由于聚焦和散射过程都会产生强烈的自旋-轨道相互作用,因此在光学显微、散射成像方面都具有重要影响。此外,在强聚焦过程中也存在轨道-自旋角动量之间的相互转化[31,32],例如在轴向涡旋光束的聚焦过程中,轨道角动量会诱导产生局部自旋角动量,驱动捕获的粒子围绕自己的轴旋转,在光束成型和光学操作方面具有重要作用。上述例子表明:光的自旋-轨道相互作用对非傍轴光场分布和性质起着至关重要的影响,自旋-轨道相互作用不可避免地出现在许多涉及亚波长尺度结构的纳米光学系统中。

不同于源自光束非傍轴性的聚焦和散射,各向异性结构产生的自旋-轨道相互作用是由于傍轴光束在介质中传输时受非均匀各向异性诱导产生和来自介质特性,属于“外”效应,同时各向异性和非均匀性为调控光场提供了更多的自由度。在各向异性介质中,沿着z轴传输的傍轴光束与xy平面相互作用就会产生强烈的自旋-轨道相互作用,产生的几何相为潘查拉特南-贝里相[33-35]。

接下来考虑傍轴光束通过平面各向异性元件的透射现象。为简单起见,使用一个相位延迟为δ的波片,光轴在xy平面的夹角为α,考虑到光轴坐标系,使用琼斯矩阵来描述光场的演化,然后旋转α角到实验室坐标系,并将矩阵改用圆偏振基矢表示为[35]

上述琼斯矩阵中非对角元的相位因子源于坐标旋转诱导的几何相位。考虑半波延迟,矩阵呈非对角化,描述了入射光的圆偏振极化σ=±1经过波片偏振态发生了反转σ=∓1,产生了几何相位差ΔΦG=2σα。通过改变各向异性轴的取向影响传输矩阵的非对角元,进而实现对光场螺旋性相关的调控。

类似的器件还有各向异性亚波长光栅[36],其空间取向可以表示为α=α(x,y),常用于实现几何相位光场调控。此外,液晶也是一种可调各向异性的光学元件,能够用来实现自旋相关的光场调控。方位各向异性波片(也称q板)是光轴在空间极坐标系内周期渐变的半波片,是目前常见的一种自旋控制的涡旋和矢量光束产生器。q板的空间变化可以表示为α=α0+qφ,其中,···,且在坐标原点存在奇点。当圆偏振光入射该波片时,偏振特性发生完全翻转并产生了相位ΔΦG=2σqφ,这就意味着透射光场获得了2qħ的内禀轨道角动量,形成了拓扑荷数l=2σq的涡旋光束。有趣的是,q=1时q板相对于传输轴具有旋转对称性,此时z方向的总角动量守恒,并且琼斯矩阵类似于非傍轴光束聚焦矩阵的横向部分。q≠1时系统对称性被打破,总角动量不守恒,部分角动量转移给了介质。不论q值是怎样的,各向异性元件都会引起光的自旋角动量和内禀轨道角动量之间的相互作用,为调控光场提供有效的途径。

近年来,随着微细加工技术的进步和亚波长光学理论的发展,超表面已经可以对相位、振幅、偏振进行亚波长量级的调控,不仅仅完成半波片的功能,利用几何相位超表面还可以实现很多功能,例如平面透镜[37]、高效全息显示[38]、宽带波前调控[39]等,并且在实现自旋轨道相互作用方面发挥着不可忽视的作用[40]。通过调节超表面组成结构单元的方位角、形状、尺寸和位置,可以获得更多调控偏振和相位的自由度。根据相位调控方式可以将超表面分为几何相位超表面、共振相位超表面、动力相位超表面、以及杂化这几种相位的超表面结构。几何相位与纳米结构共振相结合的超表面能够实现宽带消色差超构透镜[41];而利用双层几何相位超表面结合的方法,可实现高数值孔径的物镜或大角度透镜[42]等。哈佛大学Capasso课题组通过调节纳米结构的尺寸和旋转角对动力相位和几何相位进行调制,实现了手性全息成像和偏振转换[43]。基于自旋轨道相互作用和相位理论还可以设计出具有新颖功能的超表面,在光的自旋轨道角动量转换[44,45]等方面具有重要应用价值。

2.2 光的自旋-外禀轨道角动量相互作用

光的自旋-轨道相互作用导致两类几何相位:自旋重定向贝里相位和潘查拉特南-贝里相位。在旋转对称光学体系中,体现为自旋-内禀轨道角动量相互作用。而在旋转对称破缺光学体系中,体现为自旋-外禀轨道角动量相互作用[46]。两种几何相分别对应两种不同的光子自旋霍尔效应。本课题组从理论上发展了基于几何相位梯度的统一理论,来描述这两类贝里相位所导致的光子自旋霍尔效应[47]。第一类贝里相位导致的自旋霍尔位移很微弱,与光学界面的光学性质和参数有关,即动量空间的自旋重定向贝里相位梯度导致实坐标空间的位移

第二类贝里相位梯度导致的自旋霍尔位移可以很大,即实坐标空间的Pancharatnam-Berry(PB)相位梯度导致动量空间的位移

从光的自旋-轨道相互作用的发展历程来看,前一种自旋分裂的现象被普遍认为是光子自旋霍尔效应,然而后一种却不被广泛认可。但从上述分析来看,两种现象有共同的物理本质:光的自旋-轨道相互作用、自旋分裂都源于几何相位梯度。只是自旋分裂体现的方式不同,前者体现在位置空间,后者体现在动量空间。因此,将PB相位梯度导致动量空间的自旋分裂称为光子-自旋霍尔效应是完全合理的。

自旋角动量和外禀轨道角动量之间的相互作用源于麦克斯韦方程组所描述电磁波的基本性质。实质上,这种相互作用最典型的案例就是光束在空气-玻璃界面发生反射或折射,一般常用斯涅尔定律和菲涅耳方程来描述[19]。然而,这些方程只适用于单一平面波在界面上的入射,对于一个有限宽的光束,它由多个平面波组成。根据傅里叶光学的平面角谱理论,这些平面波的波矢之间存在轻微差别,导致入射平面略有不同。如图5(a)所示,xz平面为入射面,θ为入射角,傍轴光束中各个入射平面波被相对于z轴的方位角φ=ky/(ksinθ)所旋转,诱导产生了几何相位ΦG=σky2cotθ/k。沿着ky方向的几何相位梯度导致了光束沿着y方向的横移。结合界面的菲涅耳系数和反射/折射光束相似几何相位,可以得到光束自旋相关的位移的精确表达式。

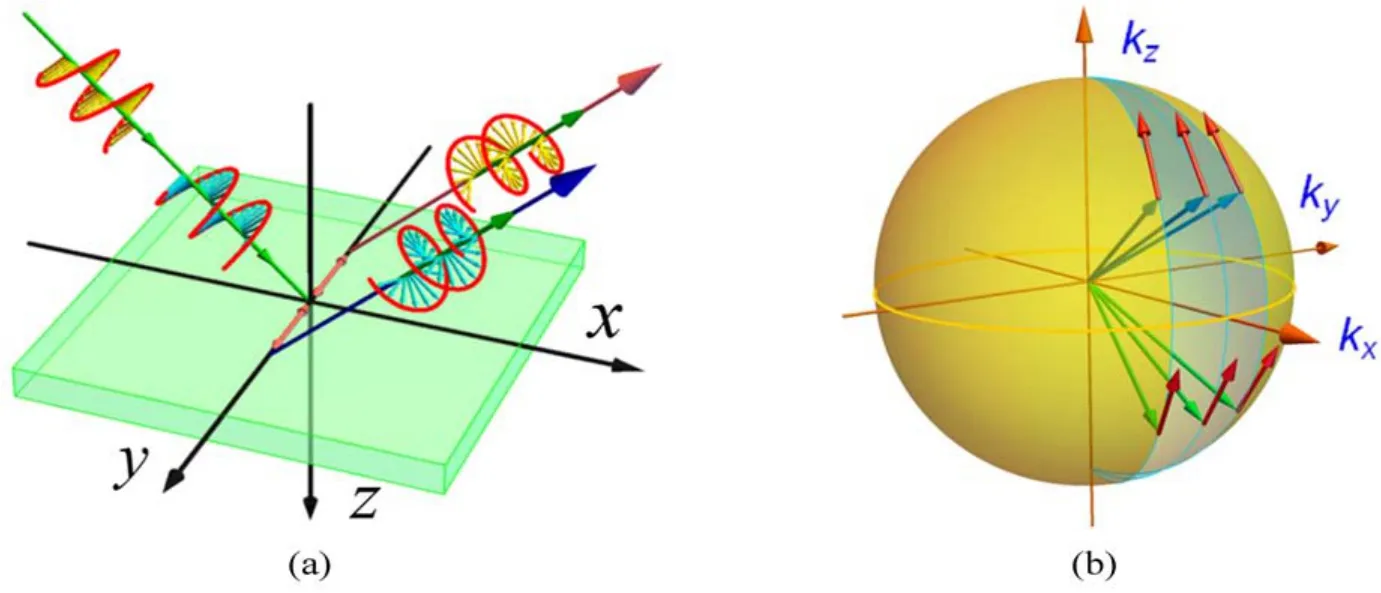
图5 光在空气-玻璃界面反射的光子自旋霍尔效应。(a)光束沿垂直于入射面方向发生横向自旋分裂;(b)波矢在动量空间发生平行移动,导致光束的不同角谱分量产生不同的偏振旋转Fig.5 The photonic spin Hall effect of light reflected at the air-glass interface.(a)The beam undergoes transverse spin splitting in the direction perpendicular to the incident plane;(b)The wave vector parallel transport in the momentum space,resulting in different polarization rotations for different angular spectrum components of the beam

以界面全反射情况而言,反射光束相对入射光束产生了自旋相关的横移,可表示为

式中σ和Δy表示反射光束的自旋性质和光束相对中心位置的位移。类似于(12)式,自旋相关的横移与界面处自旋角动量和外禀轨道角动量之间的相互作用密切相关,这种位移保证了入射和反射过程z方向总角动量的守恒

需要强调的是:伊姆伯特-斐德若夫(Imbert-Fedorov)效应与光子自旋霍尔效应并不是同一种效应,虽然两者同属光自旋轨道相互作用的典型现象,其物理根源与一种叫做Rytov-Vladimirskii-Berry(RVB)的几何相位有关。RVB相位与光的传播方向有关,比如光在介质分界面发生反射和折射导致传播方向改变而产生的附加相位就属于这一类相位。但是二者的表述方式是不同的,Imbert-Fedorov(IF)效应考虑的是左旋或者右旋圆偏振光入射,光束的螺旋性直接对应光子的自旋角动量,在光学界面处发生反射或折射后光束整体重心产生横向位移。很久之前在光的全内反射过程中就观测到这一现象。然而,过去对Imbert-Fedorov位移存在争议。直到最近,正确的理论计算、精确的测量才阐明了Imbert-Fedorov位移的物理本质,即光的自旋-轨道相互作用。在讨论光自旋霍尔效应时,经过反射后的光场被分解为左旋和右旋分量,不同分量受到光学界面电磁性质提供的“外力”作用而发生位移。总的来说,前者强调光束整体的横向位移,后者强调不同圆偏振态的自旋分裂。因此,在一般情况下这两种效应体现的光束位移是不同的。但在一些特殊情况下,例如在光束发生全反射时,两种效应体现的位移相同。

通常情况下,光在光学界面反射和折射时,光的自旋-轨道相互作用导致的自旋重定向相位梯度很小,因此导致的位置空间的自旋分裂也很小。2015年,本课题组从理论上预测并实验观察到了一种光学超表面中巨大的光子自旋霍尔效应(图6)[48]。通过控制光轴旋转率的周期就可以调控几何相位梯度。如果要实现大的自旋分裂,可以设计旋转率小的周期,从而获得大的PB相位梯度。同年,复旦大学周磊教授小组基于实空间PB相位理论[49],利用超表面在宽带产生了巨大光子自旋霍尔效应[50]。光子自旋霍尔效应与光学超表面的联合,为开发光子自旋霍尔器件开辟了激动人心的途径。除此之外,当光束穿过一个倾斜放置的偏振片时,还会产生与观察角度有关的几何光自旋霍尔效应[51]。透射光束的强度分布取决于入射偏振态,其光束重心产生一个波长量级的位移。这种现象与偏振片的材质无关,因此证明了自旋轨道相互作用的普遍特性。最近,由暨南大学Zhu等[52]提出了一种波矢改变PB相位导致的光子自旋霍尔效应,通过傍轴光束小角度入射打破旋转对称性,诱导出随着波矢线性变化的PB相位,从而导致光子自旋霍尔效应,在分离自旋态和提高传输效率方面有重要应用潜力。

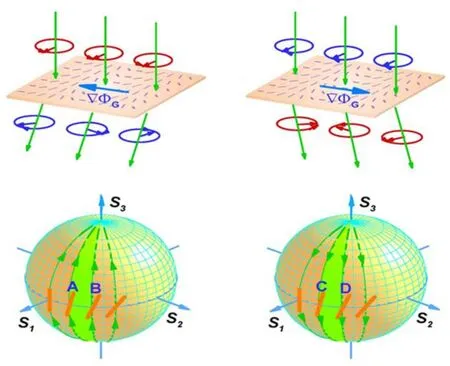
图6 超表面中的光子自旋霍尔效应和庞加莱球上相应的极化演化示意图。对于不同圆偏振的入射,超表面简单地产生相反的几何相位和相反的自旋相关动量位移[48]Fig.6 Schematic illustration of the photonic spin Hall effect in a metasurface and the corresponding polarization evolution on the Poincar´e sphere.For the incidence of different circular polarization light,the metasurface produces an opposite geometric phase and an opposite spin-dependent momentum shift[48]

自旋-外禀轨道角动量相互作用在波导结构[53,54]和等离激元超表面[55]中具有一些重要效应。德国洪堡大学Rauschenbeutel小组将金属纳米粒子置于纳米光纤表面,通过改变入射光的偏振态可以控制光纤中光的传播方向,光纤中光的传播方向也可以控制解耦光的偏振态,实现了光自旋霍尔效应和逆自旋霍尔效应[53]。借助超表面提供的满足条件的相位梯度,进而激发波导内的不同波导模式,入射光的偏振态和波长可以调控波导模式及其传播方向,实现了自旋控制波导模式的单向传输[54],整个过程实现了光的自旋角动量到外在轨道角动量的转换。另外,在圆偏振光的激发下在金属表面也会产生自旋控制的表面等离激元的定向传播[55]。

近年来,通过对近场光场的深入研究,科学家发现了另一种自旋矢量方向与光场传播方向垂直的自旋形态:横向自旋[56,57]。这种自旋态起源于麦克斯韦方程中倏逝波模式的基本自旋性质,广泛存在于结构光场中,且具有单向性激发和散射的特性。英国伯明翰大学的张霜教授小组通过调整两超构平面内旋转取向有效调节横向自旋抵消的程度,揭示了横向光子自旋体系的体态和边界态效应[58]。深圳大学杜路平教授团队通过对近场光场中自旋轨道相互作用的研究,构造了一组类似麦克斯韦方程组的自旋动量方程组,并应用该定律揭示了光学斯格明子的产生机理[59]。不同于此前通过光的电磁性质衡量自旋轨道相互作用,这种方法可以直接通过赫兹势来表征近场光场的自旋动量关系和自旋轨道相互作用。这些横向效应在利用自旋和轨道角动量进行传感、纳米计量和制造单向辐射量子器件等应用领域有着重要的前景。

3 光的自旋-轨道相互作用研究进展

光子自旋霍尔效应在任何光学界面上都是普遍存在的。在金属、单轴晶体、半导体以及纳米金属薄膜、石墨烯薄层和超表面的界面上都曾观测到自旋霍尔效应。由于每个光学器件是以有限尺寸的光束而不是平面波工作的,因此自旋霍尔效应一直存在于光界面处,不可避免地影响波长尺度的光场分布。一方面,为了保证角动量守恒,光的自旋-轨道相互作用将诱导一些奇特的效应;另一方面,结合“弱测量”的放大机制和自旋霍尔位移对材料参数的依赖使得光的自旋霍尔效应可以作为指针用于精密测量。在传统的光学界面,光子自旋霍尔效应所产生的横移值非常微小,大约只有十分之一个波长。在空气-玻璃界面,可见光波段的光子自旋霍尔位移大约只有几十纳米,因此常规的测量手段无法直接测量。弱测量的概念虽然是在量子力学的背景下提出的,但是弱值放大技术也适用于经典光。

3.1 基于光子自旋霍尔效应的弱测量技术

2008年,美国Illinois大学Kwiat课题组基于量子弱测量方法首次从实验上观测到了折射光中的光子自旋霍尔效应(图7)[18]。在光子自旋霍尔效应的量子弱测量实验中,自旋算符作为系统的一个可观测量,光的自旋-轨道相互作用体现为光子自旋霍尔效应,其自旋分离值作为自旋算符的指针。通过偏振态的前选择与后选择技术可以使指针位移得到显著放大。实验中搭建的光路如图所示,通过半波片(HWP)、透镜(L1)、格兰起偏器(P1)使得透射过可变角度棱镜(VAP)的光束建立一个合适的前选择态,再通过另一组格兰起偏器(P2)和透镜(L2)产生一个合适的后选择态。当前后选择态接近于正交时,原始位移被放大了近4个数量级,从而获得了0.1 nm级别的灵敏度。

图7 光在空气-玻璃界面反射的光子自旋霍尔效应与实验测量[18]。(a)光在空气-玻璃界面反射示意图;(b)测量光子自旋霍尔效应的弱测量装置;(c)光子自旋霍尔效应中的自旋分裂的理论与实验结果Fig.7 Photonic spin Hall effect at air-glass interface and its experimental measurement[18].(a)Schematic diagram of photonic spin Hall effect at air-glass interface;(b)Experimental set-up for observing the photonic spin Hall effect by weak measurement;(c)Theoretical and experimental results of photonic spin Hall effect

在光子自旋霍尔效应的弱测量中,有弱值放大与传输放大两种放大机制[18]。以光子自旋霍尔位移作为探针为例分析这两种机制。其中σ为泡利算符,Aw为弱值,可以表示为

式中ψi、ψf分别为偏振态的前选择与后选择。在这里后选择态与中间态接近正交。将前选择态与后选择态代入到(18)式即可得到

相对于折射光的光子自旋霍尔效应,2009年,北京大学李焱课题组利用弱测量实验观测到了空气入射到玻璃反射的光子自旋霍尔效应[60]。2011年,本课题组发现在布儒斯特角附近入射可以增强反射光场的光子自旋霍尔效应,自旋分裂值相当于折射光的50倍[61]。进一步研究表明折射率梯度可以增强或抑制光的自旋角动量到外在轨道角动量的转换,从而调控光子自旋霍尔效应。随后,在2012年本课题组通过弱测量技术观察到了纳米金属膜上的光束横向位移[62]。研究表明通过调节金属膜的厚度可以有效地控制自旋-轨道耦合效应,使得横向位移在一定范围内对金属膜的厚度敏感。因此,基于量子弱测量技术,光子自旋霍尔效应为物性参数精密测量开辟了一条全新的途径。

常规方法在测量超薄纳米薄膜的厚度(如数纳米厚的薄膜、分辨二维材料的层数等)时存在诸多不足,例如原子力显微镜方法虽然直接但须损伤样品;拉曼光谱方法虽能快速测量,但对多层二维材料(如石墨烯)的分辨结果有时并不十分准确。而由理论推导可知,光的自旋霍尔效应产生的横向位移对界面参数(如折射率、厚度等)非常敏感,因此本课题组在国际上率先提出通过探测自旋霍尔位移来精确测量薄膜材料的厚度和折射率等参数[63]。尤其对于超薄的(单原子层厚度到数十纳米范围之间)纳米薄膜测量,该方法具有非常高的精度,可以精确、无损地测量金属薄膜的厚度和分辨出数层石墨烯的层数,因而具备其它常规方法所没有的优势。2020年,Chen等[64]利用弱测量技术获得单层石墨烯的光导率作为通用常数,获得了1.5×10-8Ω-1的高测量分辨率,测量精度比传统方法提升了2个数量级(图8)。随后通过对二硫化钼薄膜光子自旋霍尔效应的研究,实现对复折射率和表面电导率的精确测量[65],建立了一种以自旋霍尔效应表征过渡金属二硫属化物光学特性的有效方法。经过本课题组十余年的努力,已经将光子自旋霍尔效应发展成为物性参数的精密测量工具。

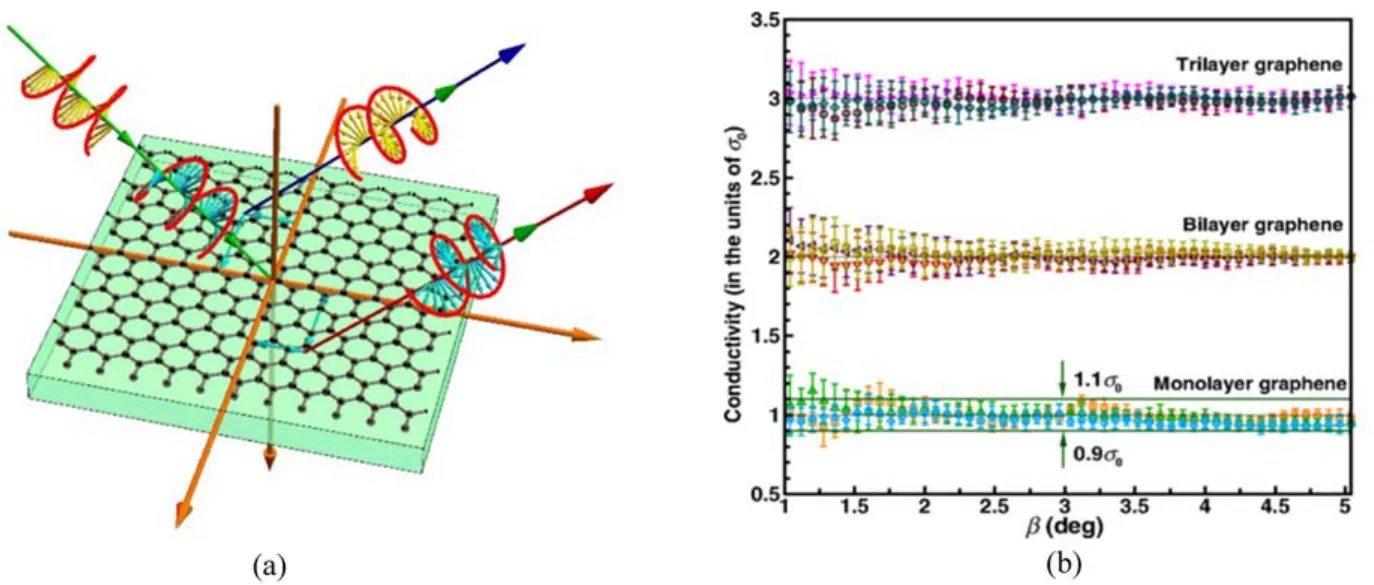
图8 光在石墨烯薄膜上反射的光自旋霍尔效应[64]。(a)线偏振光入射到薄膜上分裂成左旋和右旋偏振光;(b)基于光子自旋霍尔效应精确测量一至三层石墨烯电导Fig.8 Schematic of photonic spin Hall effect on reflection at graphene film[64].(a)A linearly polarized beam reflects on the model and then splits into left-and right-circularly polarized light,respectively;(b)Precise measurement of conductivity of several layer graphene

化学反应通常伴随着容易观察到的物理效应,例如光的发射、光谱的偏移或手性的变化。所有已知的生命形式在化学结构以及宏观解剖结构、发育和行为方面都显示出特定的手性特性。因此,化学反应的实时监测引起了极大的兴趣。通常,化学法测定反应速率可能会对反应物造成部分影响,增加了测定的难度和复杂性,而使用光学方法研究溶液的性质有助于保持原始的化学结构。2020年,本课题组结合量子弱测量,提出基于光子自旋霍尔效应实现蔗糖水解反应速率的超灵敏实时检测(图9)[66]。与传统的测量光子自旋霍尔效应的弱测量不同,这里精确测量的不是光子的自旋态,而是后选择态。后选择偏振光通过蔗糖水解过程中旋光度的变化和诱导的初始自旋相关位移来改变,通过光子自旋霍尔位移作为测量指针,量子弱测量中放大的指针位移显示出对旋光角变化。该方法获得了优于标准旋光仪的高测量分辨率,并且实现了对蔗糖溶液水解反应速率的实时超灵敏检测,在水质监测、生物、化学传感等方面具有重要应用价值。

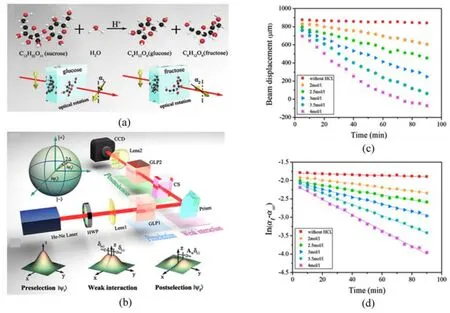
图9 基于光子自旋霍尔效应测量蔗糖的水解[66]。(a)蔗糖水解过程和手性分子光学活性示意图;(b)实验转置;(c)自旋霍尔位移与不同浓度盐酸催化水解反应时间之间的关系;(d)蔗糖在不同浓度盐酸催化下的水解速率测量实验结果Fig.9 Precise measurement of sucrose hydrolysis based on photonic spin Hall effect[66].(a)A schematic diagram of the process of sucrose hydrolysis and the optical activity of chiral molecules;(b)Experimental setup;(c)The amplified spin-Hall shifts as function of sucrose hydrolysis catalyzed by hydrochloric acid at different concentration;(d)The hydrolysis rate of sucrose catalyzed by hydrochloric acid at different concentration

另外,光子自旋霍尔效应也可以作为纳米器件尺寸起伏的测量手段。在亚波长尺度的无序几何相结构会打破光子的自旋对称性,产生意想不到的自旋光学传输现象。在无序纳米结构中光自旋霍尔效应的研究方面,以色列理工学院的Hasman教授研究团队开展了一系列创造性的工作[67-69]。纳米结构的弱无序相诱发了光子自旋霍尔效应,可以通过量子弱测量观察到;而强无序导致了动量空间的自旋分裂模式,即随机光学Rashba效应[68]。最近该团队Wang等[69]利用随机磁性超表面产生光自旋霍尔效应,用于探测纳米结构阵列的纳米级随机尺寸起伏。该方法用磁场主动破坏了光的自旋对称性,可用于探测纳米结构的深亚波长无序起伏和研究纳米磁性系统的随机涨落现象。

3.2 基于自旋-轨道相互作用的光场调控

结构光场是指具有特定强度结构、相位结构、偏振结构的光场[70]。光场调控通常主要针对光场的强度结构、相位结构、偏振结构进行调控。典型的结构光场如涡旋光场和矢量光场。涡旋光场是具有螺旋型波前和轨道角动量的特殊光场;矢量光场是指同一时刻同一波阵面上不同位置具有不同偏振态的光场,也称之为偏振态非均匀分布的光场。矢量光场这一概念是相对于标量光场提出的,通常研究的诸如线偏振、圆偏振和椭圆偏振等光场都属于标量光场,这类光场有空间均匀的偏振态分布,即波阵面上任意位置有相同的偏振态。相位作为光场的一个重要属性,对光场调控、进而对操纵光的传播行为都具有极为重要的意义。近年来,随着对光的自旋-轨道相互作用相关研究的发展,基于几何相位理论可以提供更多的自由度对光场进行调控。具有更加多样化偏振态分布的矢量光场的出现丰富了矢量光场的种类,并提供了新的调控自由度,因此被应用于光场调控、光学微加工、光学微操纵和光信息传输等领域。

具有高阶模式的激光束在粒子操控、高分辨率光学成像、量子信息等方面有着重要的应用。传统的激光模式转换基于复杂的激光腔结构或者昂贵的液晶空间光调制器。基于电介质超表面可以实现一种简单、高效的高阶激光模式转换器(图10)[71]。超表面的制备可以通过飞秒激光在熔融石英玻璃中写入空间变化的亚波长尺度凹槽来实现,其中快慢光轴分别对应平行和垂直排列的凹槽。设计超表面的关键思想是建立高阶模式的相位分布和超表面中光轴分布之间的关系。由经典的庞加莱球(Poincar´e sphere),可以清晰地发现超表面提供的相位大小为光轴夹角的两倍,通过相位和光轴的关系可以反向定制具备特定功能的超表面。因此基于PB相位超表面的光束高阶模式转换器具有高效、紧凑、即插即用等优点。此外,和动力学结合,实现两种几何相位的联合操控为光场调控提供了更多的自由度。

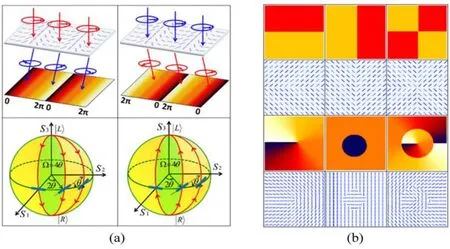
图10 基于介电超表面实现光束模式的高阶转换[71]。(a)偏振在庞加莱球极化演化产生的PB相位。诱导的PB相位随着光轴的旋转而周期性变化,当左或右圆偏振光穿过超表面时,这种变化方向相反;(b)厄米-高斯光束和拉盖尔-高斯光束的相位与对应的光轴分布Fig.10High-or dermode converter based dielectric metasurfaces[71].(a)Illustration of the polarization evolutions on Poincar´e sphere and the PB phases.The induced PB phase varies periodically with the rotation of optical axes,and this variation is in the opposite direction when left-or right-circularly polarized light passes through the metasurface;(b)Phase and corresponding optical axis distributions of high-order HG modes and LG modes

庞加莱球可以直观、形象地描述光的偏振态,它将琼斯矩阵矢量映射到一个由斯托克斯参数构成的单位球即庞加莱球的表面,该球表面任意一点对应不同的偏振态,而且庞加莱球上的不同偏振态可利用波片实现相互变换。但是,传统平面波庞加莱球只能描述具有均匀偏振态的平面波光束,而不适用于描述涡旋光束和矢量光束。类比于平面波庞加莱球,Padgett和Courtial[72]提出了轨道庞加莱球来描述涡旋光束,球的两极点对应于拓扑荷数相反的涡旋光束,赤道对应于厄米光束。而Milinone等[73]提出了高阶庞加莱球用来描述矢量光束的偏振态。高阶庞加莱球的两极点对应于圆偏振涡旋光束,赤道对应于线偏振矢量光束,介于赤道和两极之间是非均匀的椭圆矢量光。2014年,本课题组提出了一种利用非均匀双折射超表面材料产生柱矢量光束的方案(图11)[74]。基于庞加莱球的表述理论,通过改变入射光的偏振态与相位,调控光通过PB相位元件产生两自旋分量之间的振幅比与相位差,从而精确产生高阶庞加莱球上任意一点的矢量光束。

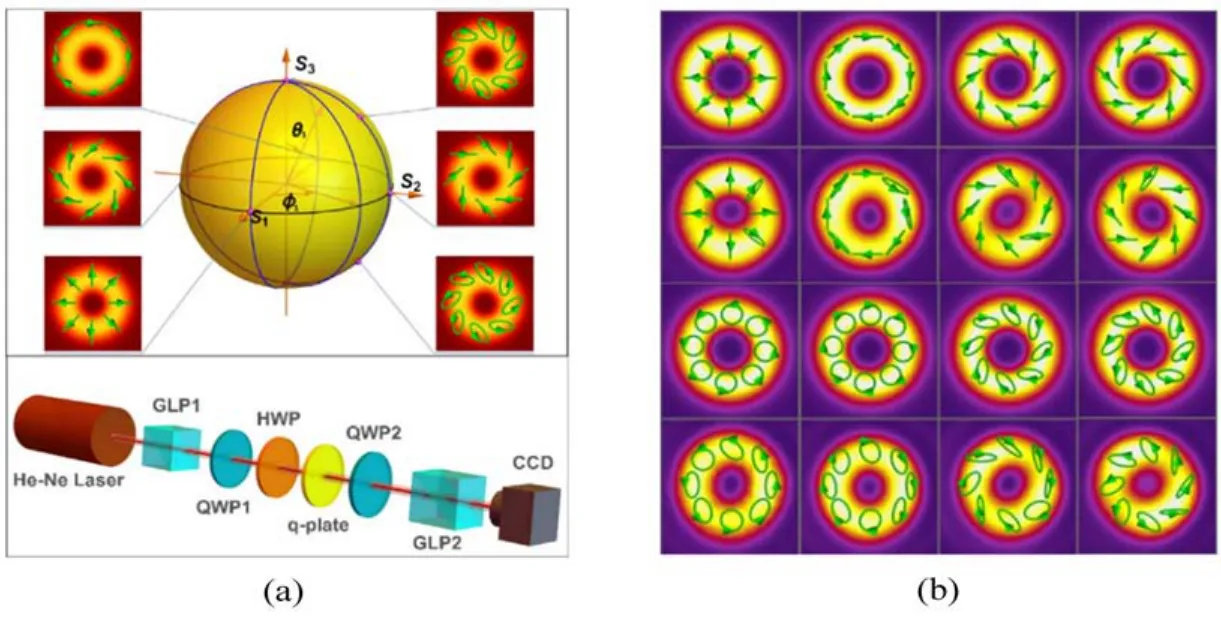
图11 产生高阶庞加莱球上的任意矢量光束[74]。(a)高阶庞家莱球上的任意矢量涡旋光束的偏振态分布和相应的实验装置;(b)基于介电超表面q板产生矢量涡旋光束的实验结果Fig.11Generation of any desirable vector beams on high-order Poincar´e sphere[74].(a)The polarization state distribution of arbitrary vector vortex beams on the high-order Poincar´e sphere and the corresponding experimental device;(b)The experimental results of the vector vortex beam generated by the dielectric metasurface q plate

根据庞加莱球表述理论,任意结构光场均可分解为两个正交基,这两个正交基具有相反的圆偏振和不同拓扑荷数的涡旋相位,由这两个正交基可以构建一种新的庞加莱球-混合阶庞加莱球[75]。不同的结构光场可由混合阶庞加莱球不同的经度与纬度表述。要产生任意的结构光场,必须找到不同经度与不同纬度之间的变换关系。通过调控两个正交基之间的相位差可以调控结构光场所处的经度,调控振幅比即可调控结构光场所处纬度。PB相位元件可以用来精确调控结构光场在庞加莱球上的演化,从而实现新型结构光场的产生和精确调控,揭示结构光场的新颖特性与演化规律。目前,已有许多产生矢量涡旋光束的方法,包括空间光调制器、基于液晶的偏振转换器、激光谐振腔等。然而,这些方法所产生的光束通常只限于特定偏振态,且具有低损伤阈值、低转换效率和大结构尺寸等缺点。因此,为了使矢量涡旋光束得到更加广泛的应用,需要找到一种高效率、更灵活、结构紧凑的产生方法。

为克服上述方法存在的问题,本课题组采用电介质q片和螺旋相位片的组合来产生混合阶庞加莱球上任意点的矢量涡旋光束[76]。混合阶庞加莱可以用于表述任意矢量涡旋光束,可以使其偏振与相位演化的物理过程变得更加直观。基于混合阶庞加莱球理论,任意的矢量涡旋光束可以分解成一个矢量光束和一个涡旋相因子。其中,矢量光束可以用一块电介质q片产生而涡旋相因子可以通过螺旋相位片来实现(图12)。通过控制入射光的偏振态,即可得到混合阶庞加莱球上相应点的矢量涡旋光束。本方案的一个重要特点是q片的结构与螺旋相位片均可制作在二氧化硅玻璃基底上,因此完全可以将两个结构集成在单个玻片上。在一块玻璃片上可以集成多个具有不同功能的光学元件,在未来的光子学与光电子学中将会有重要的应用。后续工作主要是实现系统的集成化,进一步提升操控光的偏振与相位的能力。

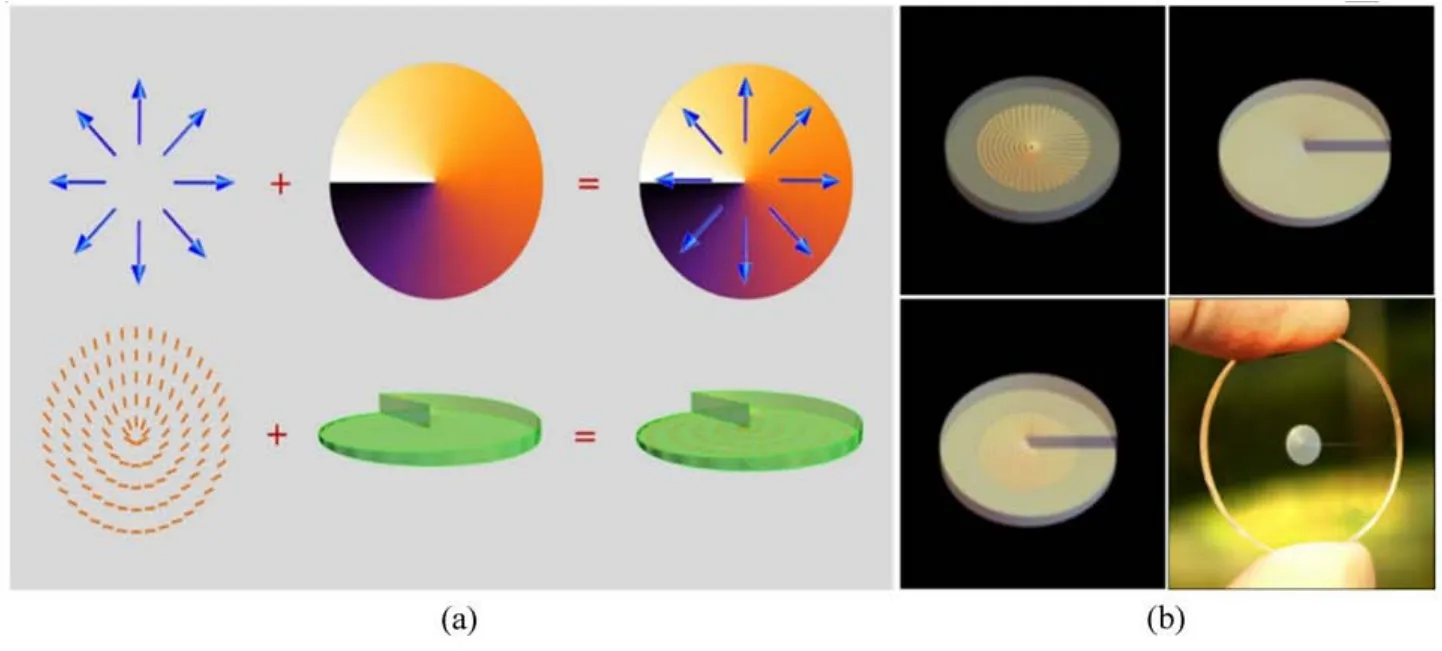
图12 (a)第一行,一个矢量涡旋光束可以分解成一个矢量偏振和一个涡旋相位。对应到第二行,矢量偏振可以用一块电介质q片产生而涡旋相位可以通过螺旋相位片来实现。将q片结构集成到螺旋相位片上,即可形成产生矢量涡旋光束的集成器件;(b)制作在螺旋相位片的q板Fig.12 (a)In the first row,a vector vortex beam can be decomposed into a vector polarization and a vortex phase.Corresponding to the second row,the vector polarization can be generated by a dielectric q plate and the vortex phase can be achieved by a spiral phase plate.Integrating the q plate structure on the spiral phase plate can form an integrated device that generates a vector vortex beam;(b)The q plate made on the spiral phase plate

3.3 光学微分运算与图像边缘检测

边缘检测是图像处理、计算机和机器视觉的基本工具。通过传统电子器件的数字计算或模拟计算实现的图像边缘检测存在计算量大、耗时长等问题。随着信息技术的迅猛发展,人们对信息处理速度的需求不断提高。数学上,微分运算是对函数局部变化率的一种线性描述。物体图像的边缘通常是光场的振幅、相位、偏振梯度较大的地方,对光场作微分运算可以提取图像的边缘信息。基于光学微分运算的边缘检测技术能够实现从整个图像中进行边缘检测的大规模并行处理,相对于传统的数字计算或模拟计算,该技术具有显著的优点,表现为光学模拟计算元件可以进行实时、连续的图像处理,几乎不需要时间。然而,传统的光学微分器由透镜和空间滤波器组成,系统复杂,不便于系统集成;此外,传统方法很难实现宽带边缘检测,而宽带边缘检测对全彩色图像处理至关重要。

浙江大学阮智超小组、北京大学李焱小组和本课题组合作,发现一斜入射光束在玻璃界面反射的光子自旋霍尔效应能实现空间微分运算,可用于对物体图像进行边缘探测(图13)[77]。光通过两个正交的偏振片使得左右旋偏振分量产生相反的位移,实现对光场空间分布作微分运算。简单分析基于光子自旋霍尔效应的光学微分运算的基本原理,考虑沿x偏振的入射光在空气-玻璃界面反射。由于光的自旋-轨道相互作用,左旋、右旋偏振光在垂直于入射面的方向发生相反方向的位移。光在反射后电场可以写为

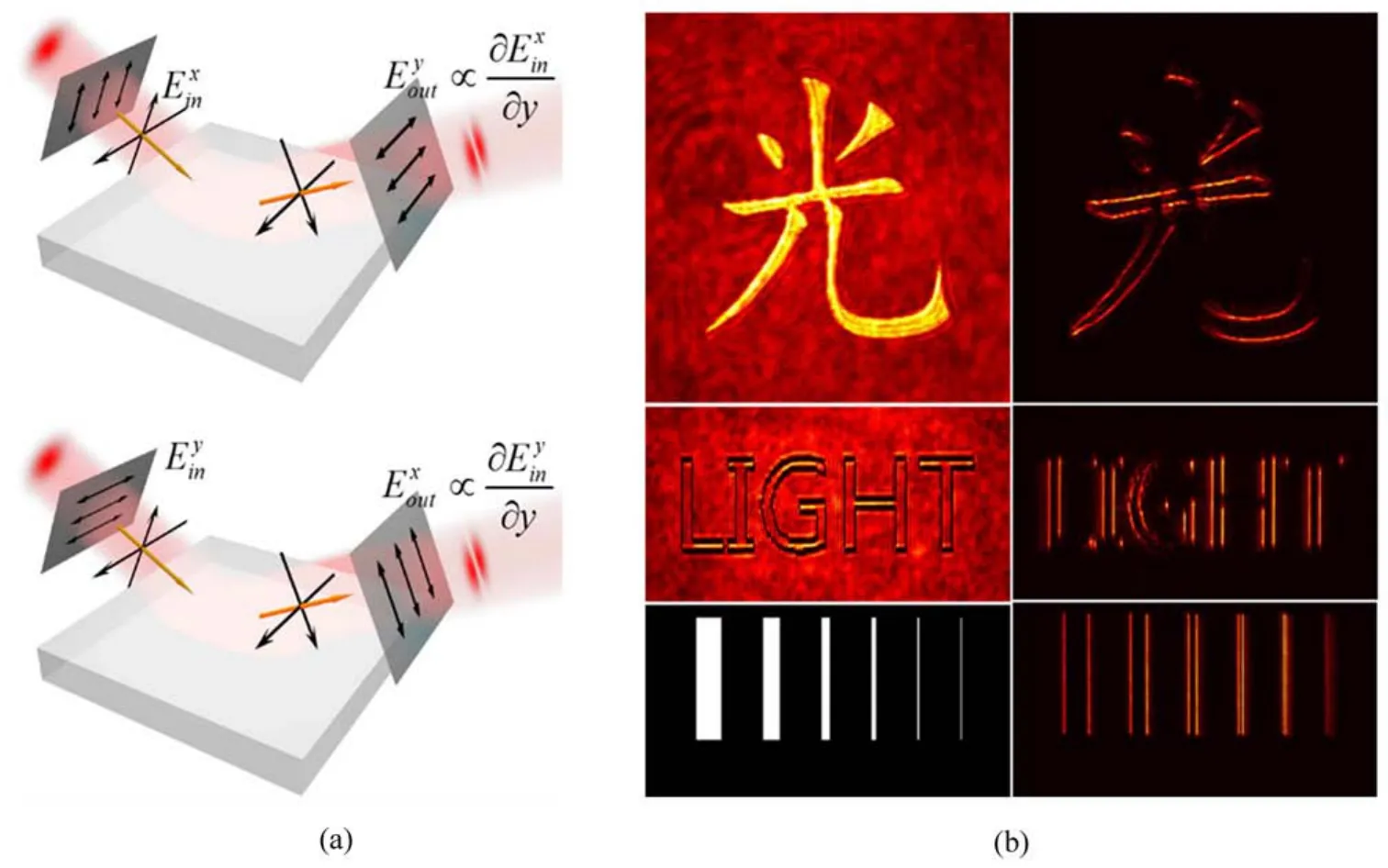
图13 基于光子自旋-霍尔效应的微分运算与图像边缘检测[77]。(a)基于两各向同性介质界面光子自旋霍尔效应的空间微分运算示意图;(b)振幅和相位变化的边缘检测实验结果Fig.13 Image edge detection based on photonic spin Hall effect[77].(a)Schematic of spatial differentiation from the photonic spin Hall effect on an optical planar interface between two isotropic materials,e.g.,an air-glass interface;(b)Edge detection for different images with either amplitude or phase modulation

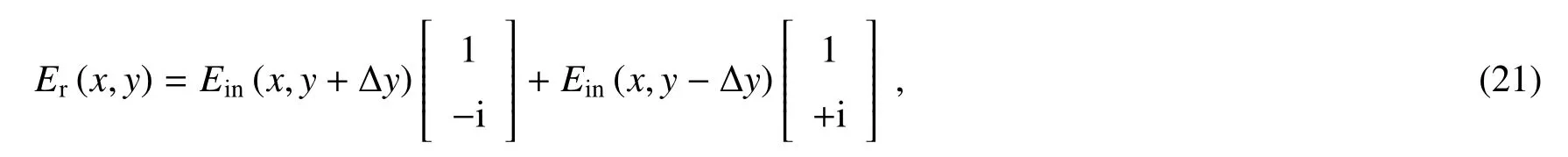
让反射光再通过一个偏振轴沿y方向的偏振片,输出光场可以表示为

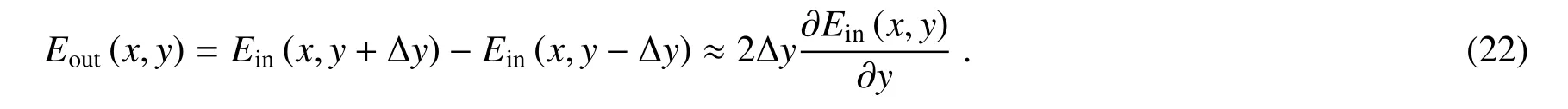
因此,基于位置空间的光子自旋霍尔效应可以实现光学微分运算,进一步可以对图像作边缘检测。也可以更加直观地理解图像边缘检测的基本原理:线偏振光界面反射后会发生光自旋霍尔效应,从而使两个圆偏振的出射光场在空间发生微小的平移,出射光场中间部分的偏振态还是线偏振,边缘部分是圆偏振,通过检偏器消除中间的线偏振,从而可以提取物体图像的边缘轮廓。

动量空间的光子自旋霍尔效应同样可以实现光学微分运算与图像边缘检测。2019年,本课题组和加州大学圣地亚哥分校刘照伟教授课题组合作,突破传统思路,提出了基于动量空间光子自旋霍尔效应的空间微分器(图14)[78]。该微分器由插入两个正交线性偏振片之间的PB相位超表面组成。基于光的自旋-轨道相互作用,位置空间的PB相位梯度导致动量空间的自旋分裂。考虑线偏振光沿着x方向入射至一光轴在y方向具有旋转率的超表面,在动量空间中传输光场可以表示为

图14 基于高效介电超表面的宽带图像边缘检测[78]。(a)基于介电超表面的边缘图像处理示意图;(b)宽带边缘图像处理。第一行显示没有微分运算的图像,照明波长分别为430、500、670 nm,超表面周期为8000µm,第二行显示了经过超表面后获得的图像边缘检测结果Fig.14 Wide-band edge detection based on high-efficiency dielectric metasurfaces[78].(a)Schematic diagram of edge detection based on dielectric metasurface;(b)Broadband edge-detection demonstration.The first row shows images without the analyzer.The illumination wavelengths are 430,500,670 nm,respectively.The images are taken with metasurface period of 8000µm.The second row shows resultant images after adding an analyzer

动量空间的自旋分裂在传输距离z后转换为位置空间的自旋分裂。让传输光再通过一偏振轴沿y方向的偏振片,输出光场可以表示为

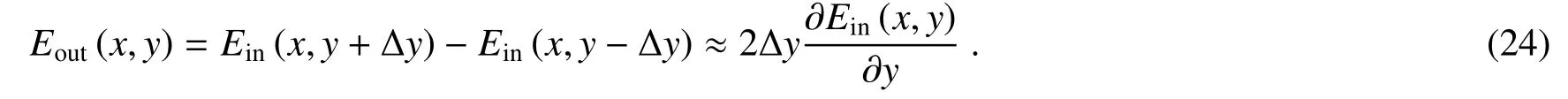
通过光的自旋-轨道耦合理论,可以实现一种基于高效介电超表面的光学边缘检测器,使其能够在光的传输过程中实时地对光场的空间分布进行微分模拟运算,进而实现物体的边缘检测。介电超表面结构通过激光直写技术制作在光学玻璃上,因此可以集成在传统的光学元件上。此外,介电超表面结构具有较高的光学效率,同时成像分辨率可达到衍射极限。特别是,在边缘检测过程中采用光的自旋-轨道耦合理论对图像进行微分运算,该物理过程与光的频率无关,因此具有宽带边缘检测能力。研究成果预期在医学成像、生物检测、化学分析、计算机视觉、自动驾驶、人脸识别等领域都具有重要的应用前景。

基于光的自旋-轨道相互作用的微分运算在显微成像中具有重要的应用前景。本课题组和刘照伟小组合作提出基于透射模式下的电介质超表面的设计,实现了具有高效率、宽带和高对比度优点的二维空间微分运算与显微成像(图15)[79]。所设计的超表面在径向方向上具有对称的相位梯度,从而可以将线性偏振光束沿径向拆分为左旋圆偏振和右旋圆偏振分量并保证二维空间微分。基于几何相位的电介质超表面没有任何共振结构,可确保在宽带工作波长(整个可见范围和近红外)下工作,从而能够对彩色图像进行边缘探测。如图15所示,光入射到物体上,然后通过位于傅里叶平面的超表面,最后在成像平面上获得其入射的边缘信息。该工作所提出的设计很容易与传统的光学显微镜相结合与集成。该边缘成像方法只需要简单地将设计的超表面插入传统的光学显微镜中,即可对振幅型物体和相位型物体进行成像。与传统的明场、相位对比和暗场成像技术相比,该边缘成像方法更加敏感,并且具有高对比度的优势,为全光图像处理和显微成像应用提供了新的可能。

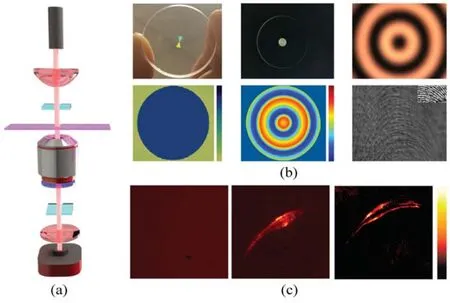
图15 基于动量空间光子自旋霍尔效应的微分显微成像[79]。(a)微分显微成像实验装置;(b)实现二维光学微分的介电超表面;(c)明场、相衬、微分显微像Fig.15 Differential microscope based on photonic spin Hall effect in momentum space[79].(a)Experimental setup for differential microscope;(b)Dielectric metasurface for two-dimensional differentiation operations;(c)Different cell images from bright-field,phase contrast,and differential microscopes

基于光的自旋-轨道相互作用的微分运算与量子成像结合为发展量子全光图像处理提供了可能。2020年,中国科学技术大学史保森教授研究组、本研究组、加州大学圣地亚哥分校刘照伟教授研究组合作[80],利用基于Sagnac环结构的高品质偏振纠缠源和激光直写的高效电介质超表面,通过改变纠缠光子对中触发光子的偏振态实现了实体成像模式和边缘探测模式的远程切换(图16)。

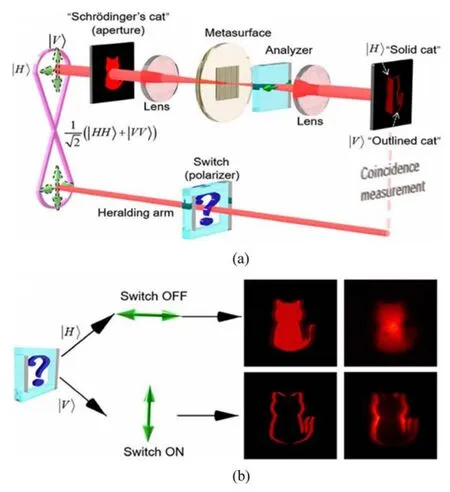
图16 量子边缘检测的超表面示意图[80]。(a)实验装置结构图;(b)触发臂的开关状态ON或OFF。当预兆臂的闲散光子投射到|H〉时,表示开关处于关闭状态并导致CCD捕获一只实体猫;当预兆光子投射到|V〉时,在开关打开的情况下获得边缘增强的轮廓猫状态Fig.16 The schematics of a metasurface enabled quantum edge detection[80].(a)Experimental schematic;(b)The switch state ON or OFF of the heralding arm.When the idler photons of the heralding arm are projected to|H〉,it indicates the switch OFF state and leads to a solid cat captured.While the heralded photons are projected to|V〉,an edge-enhanced outlined cat is obtained with the switch ON state

经过精确设计的相位超表面可以实现各种想要的功能,从而形成紧凑和集成的光学系统。当预兆光子被投射到|H〉时,边缘检测处于关闭状态,对应标准场模式;当预兆光子满足|V〉时,边缘检测开启。图16中,浅红色虚线代表电触发路径,问号意味着触发臂的光子的偏振选择是未知的。如果薛定谔猫被来自偏振纠缠源的未知线性偏振光子照亮,则图像将是常规“实体猫”和边缘增强的“轮廓猫”的叠加。在该工作中,利用偏振纠缠光源中的一个光子进行照明,由于该光子含有两种可能的偏振状态,在另外一个光子没有进行测量的时候,成像的状态是未知的,通过测量另外一个光子的状态,用于照明的光子的偏振状态也会随之确定,因此通过远程切换纠缠光子对中的用于触发的光子的偏振状态可以得到不同的成像效果,可以实现成像在正常模式和边缘探测模式的远程切换。此外,偏振纠缠光子在时间上也具有极高的关联性,在极弱光场照明、单光子CCD采集的总等效光子数相同的情况下,基于纠缠照明和符合探测相对于直接照明探测具有更高的信噪比。

除了光子自旋霍尔效应之外,基于古斯汉森位移[81]以及布儒斯特效应[82,83]等光学效应也衍生出了一系列新颖的图像边缘检测方式,未来在实现光学模拟计算等方面有望逐渐取代传统涡旋或振幅滤波器,在高速计算[84]、医学图像处理[85]、相位提取[86]、仪器校准[87]等领域都有重要的应用前景。例如,浙江大学阮智超小组提出一种可调空间光场微分器,实现对透明物体的微分相位成像,并且能够给出被观测物的光学厚度分布[86];利用光学自旋霍尔效应空间光场微分器,完全相干光或部分相干光束照射,获得相位型空间光调制器上单个像素的灰度-相位曲线,提供了一种空间光调制器校准方法[87]。

4 总结与展望

近十多年来,在国内外研究人员的共同推进下,光的自旋-轨道相互作用得到了广泛、深入的研究,取得了令人瞩目的研究成果。自旋-轨道相互作用在尺度和结构比光波长大得多的几何光学过程中通常很小,然而在纳米光学、光子学等亚波长尺度上,自旋和轨道性质会强烈耦合,发挥不可忽视的作用。一方面借助光的自旋-轨道相互作用有助于观测到光学体系中的弱效应,实现对物性参数的精确测量,发展成一种精密的计量工具;另一方面,通过人为设计纳米结构调控或增强光的自旋-轨道相互作用,为研究自旋光子学器件铺平了道路。在亚波长尺度,光的自旋-轨道相互作用为光场调控提供了额外的自旋自由度,在全光图像处理、显微成像、量子成像等领域具有重要的应用前景。完全有理由期待光的自旋-轨道相互作用的研究有助于新型光子学器件的产生,并可能衍生出一门类似于自旋电子学的新学科:自旋光子学。

光的自旋-轨道相互作用在光学模拟运算方面更是具备重要潜力,相比于传统光学微分模拟运算,基于光的自旋-轨道相互作用的光学微分器件不仅具有宽带、高对比度、高传输效率的运算特性,还摆脱了对传统光学系统的依赖,具有多功能切换、简易小巧等特点,有望推动集成光学的发展,实现更加紧凑的边缘探测系统。未来可基于该原理设计更多的光学运算器件,有望发展成为图像边缘检测的全光图像处理技术,在人工智能图像识别中有重要的应用前景。此外,将基于光的自旋-轨道相互作用和传统的显微成像技术结合,有望发展新型的微分显微成像技术,实现对透明细胞和生物组织无标记成像。将光的自旋-轨道相互作用引入到量子显微镜,利用量子纠缠可以看见前所未有的生命细节。

由于光的自旋-轨道相互作用与凝聚态、天体物理、高能物理中的自旋-轨道相互作用有高度的相似性和共同的拓扑根源,所以光的自旋-轨道相互作用的研究不仅对光学,同时还对其他学科产生重要影响。对凝聚态系统来说,由于杂质散射导致的各种内在效应的竞争以及追踪电子轨迹的不可能性,所以观测电子的自旋-轨道相互作用的实验条件非常复杂。在天体物理中,通过发光星体的自旋-轨道相互作用可以预测星体的质量。对相对论粒子来说,目前的实验能力远不够测量其自旋-轨道相互作用。因此,光的自旋-轨道相互作用作为一种很弱但又很纯的物理效应,为测量自旋-轨道相互作用这类弱拓扑现象提供了独特的机会。