有效教学实践对拔尖学生高阶思维的影响研究
——以L大学C学院为例
2022-04-14孙冬梅
孙冬梅,杨 敏
(兰州大学 高等教育研究院,甘肃 兰州 730000)
一、问题的提出
2019年,我国高等教育毛入学率达到51.6%[1],标志着我国正式步入高等教育普及化阶段。高质量人才培养是普及化阶段的重要任务[2]。为进一步提高人才培养质量,2019年底,教育部印发《关于深化本科教育教学改革全面提高人才培养质量的意见》,提出要建立起完善的人才培养质量保障体系。当前,信息技术时代已经到来,大数据、人工智能等新技术层出不穷,不断刷新着人类的生产、学习和思维方式,技术发展对人类的信息获取、吸收与驾驭能力提出了新挑战。高阶思维是以分析、评价、创造为核心的高层次认知能力,重点强调信息整合、价值判断、问题解决、实践创新等多方面的综合能力,集中体现了信息技术时代对学习者素质和能力的新要求。因此,注重学生高阶思维的培育,能够满足新时代对于学生能力的新要求,有力地提升人才培养质量。
课堂是人才培育的主阵地,课堂教学是学校促进学生发展的最主要手段,其在很大程度上决定着人才培养的质量,也极大地影响着学生高阶思维的训练与培养。在满足适当教学条件的情况下,学生的高阶思维是可以通过教学进行培养的。Ennis在总结教学实践经验的基础上提出了能够培养学生高阶思维的三种教学模式:过程模式,即在专门课程的教学中培养高阶思维;内容模式,即在具体学科课程的教学中培养高阶思维;注入模式,即把课程教学与高阶思维培养融为一体[3]。国内的相关研究也表明,教学对培养学生的高阶思维具有重要意义。钟志贤教授也强调教学设计在学生高阶思维培养中的作用,并从实践的角度提出了相应的教学策略[4]。赵永生等人在理论与实践结合的基础上,总结了能够培养大学生高阶思维教学模式的六大特征,并认为项目式教学是培养具有高级思维能力的创新型人才的最佳教学模式[5]。此外,近年来,还有很多国内学者从英语、物理、数学以及信息技术等具体学科的教学出发,探讨高阶思维的培养策略。
已有研究表明,教学与学生的高阶思维培育息息相关。但以往关于高阶思维的研究多集中于基础教育领域,且以思辨的方法为主,以实证方法研究本科生高阶思维的较少。C学院是L大学为响应国家基础学科拔尖学生培养计划(以下简称拔尖计划)而组建的,集中了学校的优势资源,致力于探索拔尖人才培养新模式。经过十年的探索,C学院的有效教学实践现状到底怎么样、拔尖学生的高阶思维现状究竟又如何、有效教学实践在多大程度上影响了拔尖学生的高阶思维,理清这些问题有助于进一步完善拔尖计划2.0时代的人才培养模式,并为全国高校解决人才培养质量问题提供可靠的案例与经验。
二、研究设计
(一)研究对象
本研究以L大学C学院全体学生(229名)为研究对象,共发放问卷229份,回收226份,回收率98.7%。其中,有效问卷206份,有效率91.2%。在这206份问卷中,男生121人,女生78人;大二学生50名,大三学生106人,大四学生22人;化学专业28人,生物专业25人,数学专业39人,物理专业21人,人文专业35人。整体来说,样本分布较为均匀,适合进行研究。需要特别说明的是:由于C学院学生均由L大学从大一全体学生中选拔而来,大二正式进入C学院,因此C学院没有大一学生。
(二)研究工具
本研究以中国大学生学习与发展追踪研究(CCSS) 2015年版绿色问卷为研究工具。该问卷是在美国大学生学习性投入调查(NSSE)问卷的基础上,由清华大学史静寰团队汉化并结合我国实际情况调整修改而来,信度效度良好。
(三)测量指标
有效教学实践是CCSS问卷中教育过程性诊断指标下的二级指标,该指标又包含课堂教学、教师反馈、激发学习志趣、评测四个三级指标,共有题项16个,四个三级指标的标准α值在0.71至0.863之间,具有较好的可信度,在此直接采用。
高阶思维在CCSS问卷中并未做明确划分,但本研究根据对高阶思维的概念定义,选取问卷的综合分析指标和学习诊断指标中的相关题项,使用SPSS工具中的因子分析方法进行筛选。通过探索性因子分析法筛选出3个因子9个题项,各因子接受检验的KMO值为0.774,Bartlett球形度检验的显著性系数为0.000,说明适合做因子分析。分析后得到的3个因子的累积方差贡献率为66.004%,说明本研究提出的三个因子可总地解释高阶思维66.004%的变异。根据因子旋转的结果,参考3个因子的题项内容,将三个因子分别命名为分析、评价、创造。
(四)数据处理
采用SPSS 24对所得数据进行分析,方法包括描述性统计、方差分析、相关分析和回归分析。
三、研究结果
(一)现状分析
C学院成立以来,积极革新教学模式,配备国内外优秀教师,关注学生个性发展与成长成才。那么,经过这十年的试验,C学院的有效教学实践与拔尖学生的高阶思维情况到底如何?本研究使用描述性统计方法对C学院有效教学实践和拔尖学生高阶思维的现状进行了分析。结果如表1和表2所示。

表2 高阶思维的现状分析
由表1可知,有效教学实践的均值为67.33,处于中等偏上水平,标准差情况较为理想,其下属的四个因子的均值也都超过50分,说明C学院有效教学实践总体发展较好。具体来看,课堂教学和教师反馈的均值分别为76.19和77.78,均高于75分,说明C学院教师在课堂教学和教师反馈方面表现优秀;测评的均值最低,为52.2分,说明C学院教师采用考核方法了解学生学习情况的频率较低。
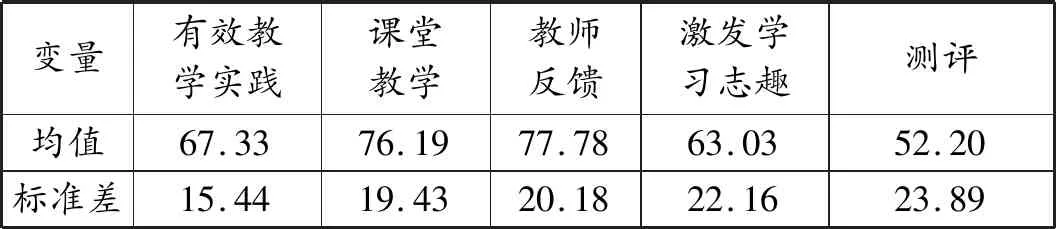
表1 有效教学实践的现状分析
由表2可知,高阶思维的均值为44.77,处于中等偏下的水平,高阶思维下属的三个因子均值情况也存在较大差异。具体来看,分析、评价两因子的均值分别为52.95和66.51,均大于高阶思维的均值,处于中等偏上的水平;评价的均值最高,为66.51,且标准差的情况较为理想,可见拔尖学生的评价能力要强于分析与创造能力;创造的均值最低,为24.26,且远低于高阶思维、分析以及创造的均值,说明拔尖学生的创造能力有待加强。
(二)差异分析
为了解拔尖学生高阶思维是否存在显著的群体差异,本研究将高阶思维作为因变量,以性别、年级、生源地作为自变量进行差异分析,结果如表3、表4、表5所示。
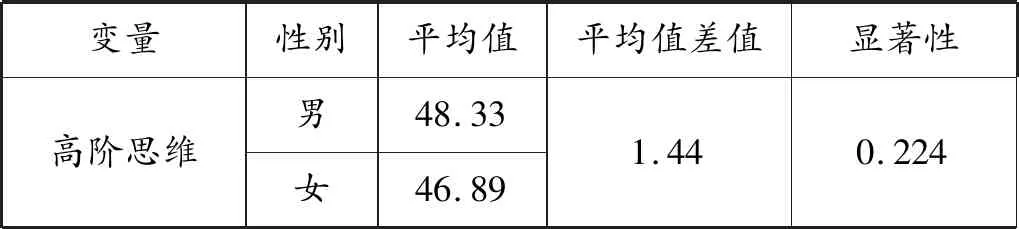
表3 性别分组平均值比较
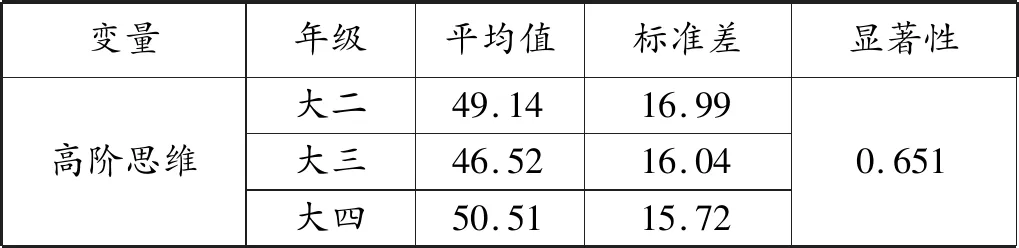
表4 年级分组平均值比较
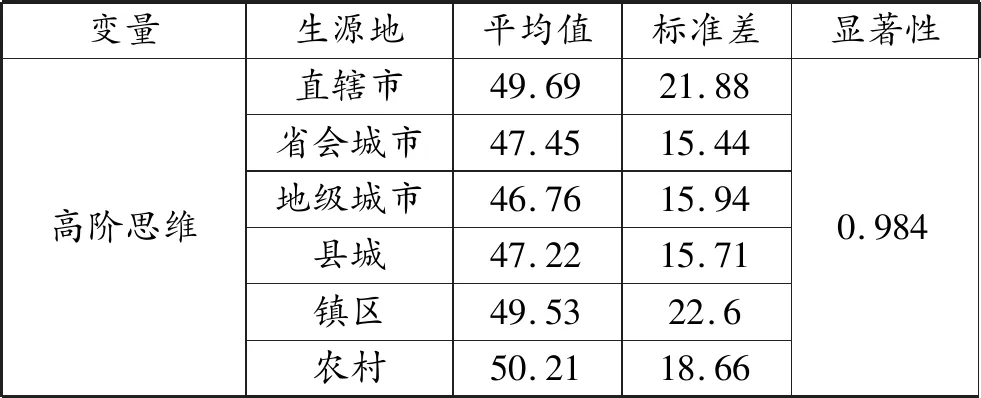
表5 生源地分组平均值比较
以性别作为自变量进行独立样本T检验,结果如表3所示。男生在高阶思维均值上高于女生,但平均值差值仅为1.44,而显著性系数为0.224,大于0.05,差异不显著。以年级为自变量进行单因素ANOVA检验,结果如表4所示,在高阶思维均值上,大四>大二>大三,但显著性系数为0.651,大于0.05,差异不显著。以生源地为自变量进行单因素ANOVA检验,结果如表5所示,在高阶思维均值上,农村>直辖市>镇区>省会城市>县城>地级城市,但显著性系数为0.984,大于0.05,差异不显著。因此,拔尖学生的高阶思维不存在显著的群体差异。
(三)相关分析
为了解有效教学实践具体是怎样影响拔尖学生高阶思维的,本研究将有效教学实践及其下属的四个因子与高阶思维及其下属的三个因子进行了相关分析,结果如表6所示。

表6 有效教学实践与高阶思维的相关分析
由表6可知,有效教学实践及其下属的四个因子与高阶思维的相关性都是显著的(显著性系数小于0.05),表明有效教学实践确实对拔尖学生的高阶思维有所影响。就相关性而言,有效教学实践与高阶思维的相关系数为0.42,为中等程度的正相关,这说明有效教学实践的提高可以在中等程度上促进拔尖学生的高阶思维发展。具体到有效教学实践下属的四个因子,其与高阶思维的相关系数由高到低排序为教师反馈、激发学习志趣、课堂教学、评测。可以发现教师反馈与高阶思维的相关系数为0.368,为中等程度的正相关,而激发学习志趣、课堂教学、评测与高阶思维则存在弱等程度的正相关,表明有效教学实践及其下属的四个因子对高阶思维都存在中等或较弱的正相关。因此,为了进一步提升拔尖学生的高阶思维,需要强化有效教学实践,尤其是增强教师反馈。
由表6还可知,有效教学实践与高阶思维下属的三个因子相关性都显著(显著性系数小于0.05),表明有效教学实践影响拔尖学生的分析、评价与创造能力。有效教学实践与高阶思维下属的三因子相关系数由高到低排序为评价、分析、创造。其中有效教学实践与评价的相关系数达到0.467,呈中等程度的正相关;而与分析、创造的相关系数均小于0.3,呈弱等程度的正相关。由此可知,有效教学实践的增强,能够提高拔尖学生的高阶思维能力,尤其是评价能力。
(四)回归分析
在相关分析的基础上,以有效教学实践为自变量,以高阶思维为因变量,进行回归分析,结果如表7、表8所示。

表7 有效教学实践与高阶思维的回归模型摘要表
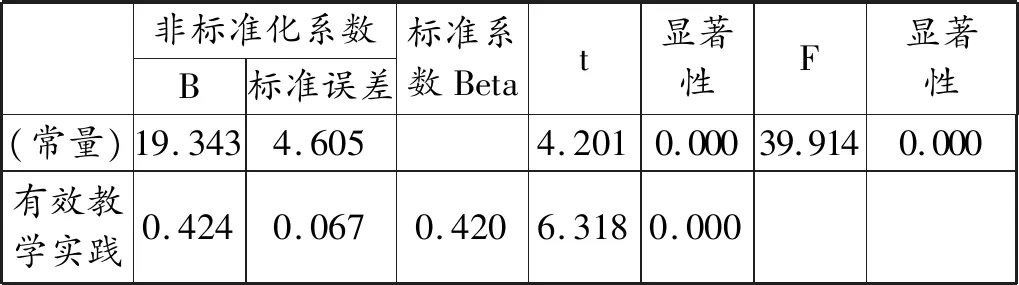
表8 有效教学实践与高阶思维的回归模型系数表
由表7可知:R为0.42,与表3中两者的相关系数相同;R平方为0.177,调整后的R平方为0.172,说明有效教学实践在17.2%的程度上能解释拔尖学生高阶思维的变化。在以上分析的基础上建立有效教学实践与高阶思维的回归方程:y=a+bx,其中y代表拔尖学生的高阶思维,x代表C学院的有效教学实践。将表8中的有关系数代入,可得到回归方程y=19.343+0.424x,表示C学院有效教学实践与拔尖学生的高阶思维之间呈正线性关系,且有效教学实践增加1分,拔尖学生的高阶思维可提高0.424分。该模型的统计量F为39.914,显著性系数小于0.01,达到了非常显著的水平,说明该模型具有统计学意义。
四、结论与讨论
(一)有效教学实践能够明显提升拔尖学生的高阶思维
由相关分析结果可知,有效教学实践对拔尖学生的高阶思维有着显著影响。具体而言,有效教学实践对高阶思维下属的各因子也有着不同程度的显著影响。其中,对评价的影响相对较大,对分析、创造的影响相对较小。通过回归分析建立起的回归方程可知,C学院的有效教学实践每增加1分,拔尖学生的高阶思维可以提高0.424分。所以,总的来说,有效教学实践能够明显提升拔尖学生的高阶思维。纵观如今的高等教育,虽然高校数量和招生规模与日俱增,但高校教学质量与人才培养质量却常常为社会各界所诟病,“水课”、教师重科研轻教学、毕业生就业难等已成为经久不衰的热点问题。人才培养的主要途径是教学,当前,要解决高等教育的质量问题,提高人才培养质量,教学改革势在必行。有效教学实践对学生高阶思维有着显著的正向影响,能够提高学生的分析、评价、创造方面的综合能力,有利于提升学生的综合素质和高校的人才培养质量,应引起各高校关注,使之成为教学改革的参考经验之一。
(二)教师反馈与激发学习志趣对拔尖学生评价能力有显著正向影响
由有效教学实践与高阶思维的相关分析结果可知,教师反馈与评价相关系数为0.422,激发学习志趣与评价的相关系数为0.384,说明教师反馈和激发学习志趣都与评价存在中等程度的正相关。需要注意的是,这里的激发学习志趣主要指教师教学与学生学习动机的关系,包括教师是否激发学生的学习兴趣、是否给与学生学习自由度、是否鼓励学生提出问题以及是否强调对问题的分析与理解这几方面;评价则是指在了解某个观点、经验、结论或推理思路等的基础上,根据一定的标准或准则做出价值判断的过程。已有研究认为增强教师反馈与学生学习动机能够提升学生的学业表现,但能否提升学生的评价能力、能在多大程度上提升学生的评价能力,尚无明确定论。教师反馈和激发学习志趣与评价存在中等程度的正相关,说明增强教师反馈和激发学习志趣都能在一定程度上提升学生的评价能力。
(三)C学院有效教学实践表现优异
根据对有效教学实践的现状分析结果可知,有效教学实践均值达到67.33,整体来看处于一个较高的水平,说明C学院在教学改革方面取得显著成效。具体来看,课堂教学、教师反馈、评测的均值分别为76.19、77.78、52.2,分别高出“985工程”院校常模5.42、20.8、12.19[6];激发学习志趣均值为63.03,低于“985工程”院校常模4.93[6]。值得注意的是,教师反馈均值远高于全国同类院校常模,而激发学习志趣均值则低于全国同类院校常模。教师反馈主要指教师在了解学生学习与发展情况的前提下,通过种种途径将情况反馈给学生,使学生明白自身存在的问题与不足并明晰改进的方法与方向。C学院教师反馈均值远高于同类院校的原因在于,C学院集中了学校的优质师资,实行小班化教学和导师制,并采用启发式、讨论式、探究式等教学方法,师生间有充足的时间进行讨论与自由问答。在此种制度的保障之下,教师能够充分了解学生情况,并将情况及时准确地反馈给学生,学生遇到的困惑与难题也能得到教师的及时解答。评测是指教师采用考试或作业等形式来了解学生的学习与发展情况。C学院评测均值低于同类高校的原因,也在于小班化教学和导师制背景下,教师可以通过师生间地有效交流而非评测来掌握学生情况,因此评测均值低也在意料之中。
(四)拔尖学生高阶思维水平有待提升
在对高阶思维的现状分析结果中,高阶思维的均值为44.77,整体来看处于一个中等偏下的水平,说明拔尖学生的分析、评价、创造方面的能力水平较低。具体来看,评价的均值最高,创造的均值最低,且两者的均值相差28.69,说明拔尖学生的评价能力远高于创造能力。评价的含义在前面部分已经做了解释。创造则是指在课程学习的基础上,完成论文、报告及其他创作任务的情况。评价均值高,说明拔尖学生基础知识扎实、思路敏捷,有着较强的分辨与判断能力。创造均值低则说明拔尖学生在创作性任务的完成上还存在短板,创造力较弱。值得注意的是,有效教学实践与创造的相关系数为0.158,为弱等程度的正相关,说明有效教学实践的增强对于拔尖学生创造能力的提升作用较为有限。已有研究认为,课题研究式学习与项目创作式学习能够提升学生的创造力,但如何进一步提升学生的创造能力以及高阶思维水平仍是一个需要且值得进一步研究和探讨的问题。
