化学计量比对镓酸镁尖晶石陶瓷微波介电性能的影响

2022-04-14徐鹏宇郑凯平涂兵田

人工晶体学报 2022年3期

杨铭，徐鹏宇，王斌，郑凯平，涂兵田，王皓

(武汉理工大学材料复合新技术国家重点实验室，武汉 430070)

0 引言

近几十年来，微波介质陶瓷已被广泛应用于全球定位系统和无线局域网等无线通信系统的谐振器、滤波器和天线中[1]。由于需要将其作为微波电路、基片和无源元件的先进材料使用，与低介电常数、高品质因数(Q×f)相关的微波材料研究得到越来越多的关注[2]。

目前，典型的低k微波陶瓷材料包括Al2O3、硅酸盐和尖晶石型铝酸盐MAl2O4(M=Mg, Zn)等[3]。由于氧化铝和硅酸盐陶瓷往往存在品质因数较低的缺点[4-5]，近年来越来越多的研究集中在AB2O4尖晶石型微波介质陶瓷上。这类陶瓷普遍品质因数高[6-7]、具有很好的温度稳定性，且密度低、原材料便宜，具有可观的产业化前景[8]。然而，现有MgAl2O4、ZnAl2O4和Mg2TiO4等尖晶石陶瓷的谐振频率温度系数(τf)绝对值相当大[9-12]，对实际应用不利。因此，亟待寻找一种具有近零τf值，且微波介电性能优良的新型尖晶石陶瓷材料[13]。

MgGa2O4是一种新型单相微波陶瓷材料。Wu等[3]在1 410 ℃下采用固相烧结法制备出了具有优异微波介电性能的MgGa2O4尖晶石陶瓷，其相对介电常数εr= 9.54、Q×f=117 000 GHz，并且τf值接近于零(-4.0×10-6/℃)，是很有前途的毫米波器件候选材料。

改变组成和晶体局域结构是调节尖晶石型陶瓷微波介电性能的重要手段。Lu等[14]通过Cr3+取代Ga3+影响尖晶石结构中的八面体倾斜和近程阳离子分布有序度，降低了晶体本征介电损耗，从而提高了Zn(CrxGa1-x)2O4陶瓷的微波介电性能；Zheng等[15]通过Zn2+取代Mg2+使晶格略微膨胀，在提高(Mg1-xZnx)Al2O4陶瓷Q×f的同时，使τf值更接近零。

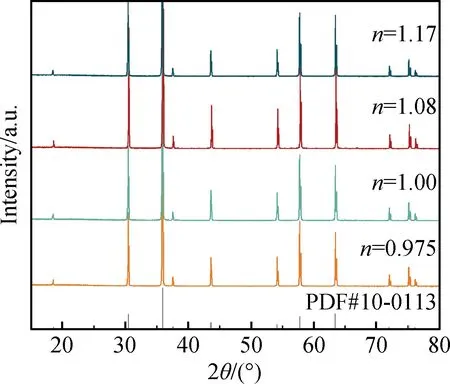
理论研究表明，处于四面体的阳离子与氧离子形成强化学键时，对介电损耗的贡献小，有助于提高Q×f值[16]。因此，在不改变尖晶石元素组成，即τf变化很小的情况下，有望通过调节化学计量比来改变阳离子分布，从而提高尖晶石氧化物的品质因子。这种手段已在铝酸盐尖晶石系统如MgO·nAl2O3和ZnO·nAl2O3中被证明是简单而有效的[17-18]，化学计量比的变化导致晶体结构改变，从而影响尖晶石氧化物的介电性质。例如，Takahashi等[19]在Mg0.4Al2.4O4陶瓷中通过增大铝含量和引入阳离子空位得到较低的εr值，同时尖晶石晶格中阳离子分布的改变使四面体化学键的共价性增大，显著提高了陶瓷的微波介电性能；Xu等[20]合成了具有缺陷结构的ZnO·nAl2O3尖晶石陶瓷，引入的铝离子优先占据晶格四面体位置，有助于降低介电损耗，提高Q×f值。在MgO-Ga2O3二元体系相图中，镓酸镁尖晶石可在较大的固溶范围内形成[21]，其组成能够在0.975

本工作的目的是研究化学计量比对镓酸镁尖晶石陶瓷晶体结构和微波介电性能的影响，从而构建组成-结构-性能之间的关系，以期制备出一种Q×f值较高、τf值近零的镓酸镁微波介质陶瓷。首先，通过固相反应法合成纯相MgO·nGa2O3(n=0.975、1.00、1.08、1.17)尖晶石粉体，无压烧结制备出一系列具有相近致密度(～98%)的MgO·nGa2O3微波介质陶瓷。然后结合XRD Rietveld全谱拟合方法和键价理论模型，研究组成对晶体结构与本征性质如晶格常数、无序度、键强以及热膨胀系数等的影响，最后评价了MgO·nGa2O3陶瓷的微波介电性能。

1 实验

1.1 样品制备

采用高纯度MgO(99.99%，质量分数)和Ga2O3(99.99%，质量分数)粉体为原料，按照摩尔比n(Ga2O3)/n(MgO)=0.975、1.00、1.08、1.17混合均匀后，经过1 025～1 175 ℃下固相反应得到MgO·nGa2O3粉体。使用压片机对粉体轴向加压30 MPa制成φ20 mm的陶瓷素坯，经200 MPa冷等静压成型5 min，然后在1 450 ℃下进行无压烧结4 h，得到厚度分别为2 mm和8 mm的致密MgO·nGa2O3微波介质陶瓷。

1.2 样品表征

采用X射线衍射(XRD，德国，Bruker，型号Model D-8 ADVANCE)表征粉体和块体的物相组成，用于结构精修数据的2θ角范围为15°～145°、步进速度为3(°)/min；用电感耦合等离子体原子发射光谱仪(ICP-AES，美国，Agilent，ICPOES 730)测定粉体中Mg和Ga的含量；确定物相组成与化学组成后，利用XRD Rietveld全谱拟合软件Fullprof进行晶体结构精修。

采用扫描电子显微镜(SEM，日本，Hitachi，型号S-3400N)观察烧结块体的显微形貌；使用阿基米德排水法测量烧结样品的密度；利用精密阻抗分析仪(美国，Agilent，型号HP4294A)在1 MHz下进行相对介电常数的测量；采用矢量网络分析仪(美国，Agilent，型号HP8722ET)测量1～18 GHz下样品的εr、Q×f和τf，τf的测量温度范围为25 ℃到80 ℃。

2 结果与讨论

2.1 晶体结构分析

MgO·nGa2O3的晶体结构符合阳离子无序尖晶石结构模型[22]，并受其化学组成约束。富镓MgO·nGa2O3(1

图1是MgO·nGa2O3粉体的XRD Rietveld全谱拟合图谱。可以看到，拟合曲线(黑色)与实验测定数据吻合较好，且均为单一的尖晶石结构(空间群Fd3m)。全谱拟合得到的峰形因子(Rp)、加权峰形因子(Rwp)和拟合优度(χ2)如表1所示，其中Rp均小于7%，Rwp均小于10%，拟合优度均小于1.65，表明拟合较好，即全谱计算拟合结果可靠。

图1 MgO·nGa2O3的全谱拟合XRD图谱Fig.1 Rietveld plots from XRD data of MgO·nGa2O3

通过MgO·nGa2O3粉体的晶体结构精修，获得了晶格常数(a)、阴离子位置参数(u)、密度以及阳离子无序度(i)等晶体结构参数，如表1所示。与MgGa2O4相比，非化学计量MgO·nGa2O3的i较小，表明阳离子无序度较高，且由于Mg2+的半径大于Ga3+，随着n值的增大，Ga3+相对含量增大，故晶格常数减小，尖晶石的分子体积也相应减小。

表1 MgO·nGa2O3粉体的晶体结构参数Table 1 Crystal structure parameters of the MgO·nGa2O3 powders

2.2 陶瓷物相组成与显微结构分析

图2为MgO·nGa2O3陶瓷的XRD图谱。由图可见，当改变化学计量比时，陶瓷样品均保持单一的尖晶石结构，没有检测到第二相。

图2 MgO·nGa2O3陶瓷的XRD图谱Fig.2 XRD patterns of MgO·nGa2O3 ceramics

图3是MgO·nGa2O3陶瓷致密度随组成的变化情况。由图中可知，陶瓷的密度都已达到理论密度的98%。并且当n=0.975、1.08和1.17时，MgO·nGa2O3陶瓷的致密度相较于MgGa2O4呈现出减小的趋势，说明Mg2+或Ga3+取代均会阻碍陶瓷的致密化，从而提高镁镓尖晶石陶瓷的烧结温度。

MgO·nGa2O3陶瓷样品的显微形貌如图4(a)～(d)所示。当n=1.00和0.975时，气孔较少，且存在少量晶粒内气孔；随着n值的增大，陶瓷的致密化程度降低，并且晶粒内和晶界处均有气孔出现。此结果也与图3相符。

2.3 相对介电常数εr分析

陶瓷的相对介电常数主要由本征因素(离子的极化等)和非本征因素(密度、气孔、晶界等)共同影响[26]。如图3所示，不同n值的MgO·nGa2O3陶瓷均达到～98%的致密度且孔隙率低，故极化率是影响其相对介电常数的主要因素[27]。

图3 MgO·nGa2O3陶瓷相对致密度与组成的关系曲线Fig.3 Relationship between relative density and composition of the MgO·nGa2O3 ceramics

根据分子极化率的加和法则[28]，可以计算出MgO·nGa2O3的分子极化率。各离子的极化率通过Shannon的研究获得[29]：

α(Mg4/(3n+1)Ga8n/(3n+1)O4)=[4/(3n+1)]α(Mg2+)+[8n/(3n+1)]α(Ga3+)+4α(O2-)

(1)

式中：α(Mg2+)=1.33、α(Ga3+)=1.50、α(O2-)=2.00。

图4 MgO·nGa2O3陶瓷的刻蚀表面SEM照片Fig.4 SEM images of etched surface of MgO·nGa2O3 ceramics

为了阐明晶体组成和结构对相对介电常数εr的影响，根据上述式(1)及表1中的晶格常数a，计算得到不同组成下晶体的分子极化率(αD)和分子体积(Vm)。如表2所示，两者均随n值的增大而单调减小。

此外，晶体的相对介电常数还可以通过Clausius-Mosotti方程进行计算：

(2)

式中：αD为分子介电极化率；Vm为摩尔体积；b=4π/3。如表2所示，1 MHz条件下得到的相对介电常数实验值与理论值接近，变化趋势也相同，说明通过Clausius-Mosotti方程计算的结果是适用于本研究的。

在MgO·nGa2O3尖晶石中，镓离子的离子极化率(1.50)比镁离子(1.33)更高，但随着n值的增大，Ga3+以2∶3的比例取代Mg2+。故结合MgO·nGa2O3组成和晶体结构的变化，当n值逐渐增大时，在分子极化率与分子体积的共同影响下，1 MHz条件下MgO·nGa2O3陶瓷的相对介电常数先增大后减小。

表2中MgO·nGa2O3陶瓷在不同频率条件下测试得到的εr值十分相近，表明没有额外的极化机制影响，不同条件下相对介电常数存在微小差异的原因可能是测试方法的不同。14 GHz下MgGa2O4陶瓷的εr为9.42，这个结果与Wu等[3]得到的MgGa2O4的εr值(9.45)非常接近。MgO·nGa2O3陶瓷与MgAl2O4(8.75)[9]、ZnAl2O4(8.50)[30]和ZnGa2O4陶瓷(10.20)[13]的εr值相近，相对较低的εr值使这些尖晶石陶瓷在高频器件领域拥有广阔的应用前景。

2.4 品质因数Q×f分析

陶瓷的微波介电损耗与晶格振动引起的本征损耗有关[31]。如表2所示，MgO·nGa2O3陶瓷的品质因数Q×f随n值的增大而减小。其中MgGa2O4陶瓷在14 GHz频率下的品质因数达到137 235 GHz，与Wu等[3]得到的MgGa2O4陶瓷Q×f值(117 000 GHz)接近，并且远高于MgAl2O4陶瓷(68 900 GHz)[9]和ZnGa2O4陶瓷(94 600 GHz)[13]。另外，MgO·0.975Ga2O3陶瓷的Q×f值最大，达到165 590 GHz。

获得表1的晶格参数后，为了根据四、八面体振动模之间的协调性判断对应的本征介电损耗变化[24]，采用Brown提出的键价模型[32]计算了多面体的键力常数(FC)。目前，此模型在尖晶石中已被广泛应用[33-34]。在尖晶石晶体结构中，j和k原子形成的化学键键价通过式(3)计算：

(3)

式中：Sjk为键价；Rjk为由原子j和k组成化学键的键长；R0和b为键价参数，b为0.037 nm，室温下Mg—O与Ga—O键的R0值分别为0.169 3 nm和0.173 0 nm[35]。

键价的组成加权平均值(SAve)为[33]:

(4)

式中：Xj和Yk分别是阳离子和阴离子在配位多面体中的比例分数。FC通过式(5)计算：

(5)

式中:β取0.23 nN·nm2·electrons-2。

根据键价模型计算的结果，随着n值的增大，MgO·nGa2O3四面体键强的增强以及八面体键强的削弱，使四八面体振动模之间的协调性降低，整个晶格振动模的一致性下降，故对应的本征介电损耗增大，Q×f值降低[24]。此外，尖晶石晶格中的阳离子分布与Q×f值也有很好的相关性[36]：与MgGa2O4相比，其他组成镁镓尖晶石的阳离子有序度下降，晶格中四面体格位上的三价阳离子减少，介电损耗增大，从而使Q×f值下降[18]。综合以上影响因素，MgO·nGa2O3陶瓷的Q×f值随n值的增大而减小。

表3 MgO·nGa2O3的化学键性质参数Table 3 Chemical bond property parameters of MgO·nGa2O3

2.5 谐振频率温度系数τf分析

由表2可见，不同组成MgO·nGa2O3陶瓷的τf均为负，数值在-19×10-6～-5×10-6/℃之间。其中MgGa2O4陶瓷的τf=-5.45×10-6/℃，该结果与Wu等[3]制备的MgGa2O4陶瓷τf值相近(-4.0×10-6/℃)，且与报道的MgAl2O4陶瓷(-75×10-6/℃)[9]及ZnGa2O4陶瓷(-27×10-6/℃)[13]τf值相比要更接近于0。

若陶瓷体系中未形成明显的相变化，影响τf的因素是十分复杂的[37]。根据公式τf=-1/2τε-α可知，谐振频率温度系数与陶瓷材料的热膨胀系数(α)和介电常数温度系数(τε)均相关[38]。MgO·nGa2O3晶体的热膨胀系数可根据以下公式计算得到[33-39]：

(6)

(7)

(8)

如表2所示，τf值与热膨胀系数α呈现相反的变化趋势，说明热膨胀系数的变化可能会在一定程度上影响MgO·nGa2O3体系的温度稳定性[27]。同时，晶体结构的变化可能会影响化学键的性质，如四、八面体键价等，从而使τε改变[40-41]，且随n值的增大，这种影响的程度逐渐加深，表现为τf值的显著变化。尽管如此，本工作得到的不同组成MgO·nGa2O3陶瓷均具有接近零的τf值，说明镁镓尖晶石陶瓷的谐振频率在温度变化时较为稳定，是理想的微波介质材料。