Ti3(ZnxAl1-x)C2固溶体热学、电学和力学性质的理论研究

邓斐然,徐 敏,苗 峰,黄 毅,冯世全,宋明泽,肖晨达,林园园,李慧敏

(1.西南民族大学电子信息工程国家民委重点实验室，成都 610041；2.郑州轻工业大学磁电信息功能材料重点实验室，郑州 450002)

0 引 言

MAX相是三元层状化合物[1-3]，其晶格结构属于六方晶系，空间群为P63/mmc，分子通式为Mn+1AXn[4-6]，其中M代表过渡族金属元素，A代表主族元素(通常为ⅢA和ⅣA族元素)，X代表碳或氮，n=1, 2, 3…，当n=2时，分子通式M3AX2称之为312相材料。过渡金属M与C或者N组成的Mn+1Xn单元与主族元素A原子面交互迭排，从而构成了独特的结构，使得MAX相材料具备陶瓷材料和金属材料的双重性质[7-8]。MAX相材料不仅具有良好的导电和导热性，以及高屈服强度抗热震能力和机械可加工性等性能，而且具有较高的断裂韧性、熔点和热稳定性，以及优异的抗氧化和耐腐蚀性等性能[9-11]，同时具有较好的自润滑性以及相对较低的摩擦系数，这使得该相材料适合应用在高铁列车、新能源汽车、手机等电子设备以及航天航空等领域。MAX相材料以其独特良好的性能引起了无数材料工作者的关注和研究[12]。

1994年，Pietzka和Schuster等[13]发现Ti3AlC2材料综合了金属和陶瓷的双重优良性能，具有良好的导电和导热性、高屈服强度、低硬度、优异的抗氧化和热稳定性以及高弹性模量导致较好的机械可加工性等。Ti3AlC2材料具有六方层状结构，由紧密堆积、交替排列的Ti6C八面体层和纯Al原子层交互迭排而成，由两个Ti3AlC2分子构成一个单胞。

2016年，Wang等[11]首先系统地研究了Ti3(SnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶体体系，并分析其结构、能量、稳定性、电学、力学和热学性质。研究表明:当掺杂了0.75浓度(原子数分数)的Sn原子时，该固溶体体系拥有最大的体积模量；当掺杂了0.5浓度的Sn原子时，该固溶体体系拥有最大的剪切模量。

2019年，李勉等[14]探索合成出Ti3ZnC2，以Ti3AlC2为前驱体，用ZnCl2作为Zn源，通过拥有强路易斯酸性的ZnCl2去腐蚀Ti3AlC2的A层，在一定程度上促使Zn原子进入到A层，导致与Al原子发生完全置换反应，从而得到Ti3ZnC2化合物。测定其晶格常数为a=0.307 4 nm，c=1.860 2 nm。通过弹性常数满足Born稳定判据得知其力学稳定并结合声子谱无虚频可知该研究的Ti3ZnC2结构稳定。这说明在室温下可以通过材料合成得到Ti3ZnC2相。

目前已发现70多种MAX相材料，这一领域也吸引了越来越多的研究人员，但关于Ti3(ZnxAl1-x)C2的电子结构理论、热力学理论以及弹性性能相关的研究目前还鲜有报道。国内外关于新型MAX相陶瓷金属材料的研究主要基于三个方面：(1)MAX相材料合成纯度的提高；(2)MAX相材料性能的优化加强；(3)新型MAX相材料的稳定合成[15]。而MAX相的众多性质都是电子结构性能在起决定性因素,因此探究材料特性最重要的是先研究其电子结构、成键特性以及弹性性能[16-19]。本文采用第一性原理的密度泛函理论平面波赝势法, 通过投影缀加波(PAW)和广义梯度近似(GGA)对Ti3(ZnxAl1-x)C2固溶体体系进行系统研究，对比并分析其电子结构、成键特性和弹性性能的变化趋势，以及掺杂Zn的浓度对Ti3(ZnxAl1-x)C2固溶体体系性质的影响。

1 计算方法

本文采用基于密度泛函理论(DFT)的PAW对Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶体体系使用VASP(Vienna Ab-initio Simulation Package)进行模拟理论计算[20]。在本体系的计算中，体系波函数由平面波基组展开，选取PAW描述体系芯电子与离子实间的相互作用，电子与电子间的交换关联势选用GGA[21]下的PBE泛函描述[21-22]。动能截断值在测试后设为520.0 eV，Ti3AlC2和Ti3ZnC2的布里渊区(Brillouin zone)积分k网格采用Gamma为中心的13×13×2取样方法[23]，Ti3(ZnxAl1-x)C2固溶体体系建立了2×2×1的超胞，其布里渊区积分k点网格采用Gamma为中心的6×6×2取样方法。同时，为确保在平面波基水平上体系的能量和结构实现收敛，设其自洽精度为10-5eV/atom，原子间相互作用力收敛标准为10-1eV/nm。

2 结果与讨论

2.1 电子结构性质

三元层状化合物Ti3AlC2和Ti3ZnC2晶体结构与其他312型MAX相结构相似，其晶体结构属于六方晶系，空间群为P63/mmc(No.194)。其中晶体中对应原子的空间占位分别是：Ti1(0,0,0)、Ti2(1/3, 2/3, 0.127)、Al/Zn(0, 0, 1/4)、C(2/3, 1/3, 0.431)。Ti3AlC2和Ti3ZnC2的晶格模型以及Ti3(ZnxAl1-x)C2(x=0.25, 0.5, 0.75)固溶体体系2×2×1超胞的晶格模型如图1所示，图1可以看到紧密堆积、交替排列的Ti6C八面体层和Al/Zn原子层交互迭排而构成的六方层状结构[24]，该层状结构在层间易于滑移，使其拥有较好的自润滑性，这对于Ti3(ZnxAl1-x)C2固溶体体系的性质而言有很重要的意义。

通过VASP软件对Ti3(ZnxAl1-x)C2固溶体体系进行结构优化计算，得到该体系稳定的晶格结构。计算得到优化后的晶格常数和该体系相关的理论值与实验值列在表1。通过表1可以看出，理论计算值与实验值均符合得很好，计算结果是可靠的。

本文在进行晶胞结构优化后，得到最稳定状态下的能量，从而计算出Ti3(ZnxAl1-x)C2固溶体体系的结构模型的形成焓(ΔH)，该公式如下：

ΔH=[Etot(Ti3(ZnxAl1-x)C2, cell)-8xE(Zn)-8(1-x)E(Al)-24E(Ti)-16E(C)]/48

(1)

式中：Etot(Etot(Ti3(ZnxAl1-x)C2, cell)是Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶体每个体系最稳定状态下的总能量，则E(Ti)、E(Zn)、E(Al)和E(C)分别是Ti、Zn、Al和C结构晶胞中单个原子最稳定状态下的能量。得到的结构模型的形成焓(ΔH)对于判断材料是否拥有良好的热力学稳定是必不可少的条件。从表1中可以看到，其值均为负数，这表明Ti3(ZnxAl1-x)C2固溶体体系的结构模型均是符合热力学稳定的。

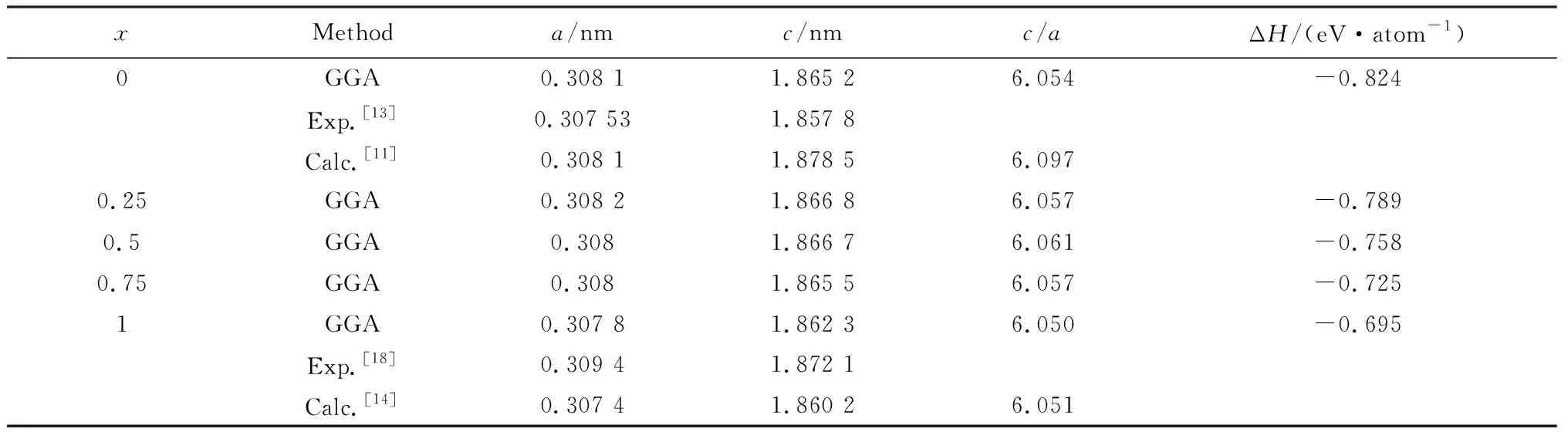
表1 Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶体的晶格常数和晶格形成焓Table 1 Lattice parameters and enthalpy formation energy for Ti3(ZnxAl1-x)C2 (x=0, 0.25, 0.5, 0.75, 1) solid solutions

为了解释Ti3(ZnxAl1-x)C2固溶体结构的本征稳定性，在优化后的晶胞结构的基础上，通过VASP的DFPT方法计算该材料的声子色散关系[25]。声子色散关系图解释声子频率在布里渊区内沿着高对称点方向的晶格振动谱，其横坐标是布里渊区的高对称点，纵坐标是经过每个高对称点的声子振动频率。从图2可以看出，声子色散的频率在整个布里渊区内都是在零点(0 THz)以上的，即没有虚频(负频)出现，预示着该晶体结构具有本征值稳定性，这也代表着Ti3(ZnxAl1-x)C2固溶体体系的结构模型是符合动力学稳定的。除此之外，在声子色散关系图中G点附近的光学分支的声子频率均有不同，导致离子键存在于在该晶体中；并且可以看到在M-K和H-L区间有两个对应着声子色散关系图中平缓的带，说明在这个位置产生了局域化特征，使其产生强烈的晶格振动。

图2 Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶体的声子色散关系Fig.2 Phonon dispersion spectra of Ti3(ZnxAl1-x)C2 (x=0, 0.25, 0.5, 0.75, 1) solid solutions

在晶胞结构优化的基础上，对Ti3(ZnxAl1-x)C2固溶体进行了电子结构方面的计算，得到总态密度(TDOS)和分波态密度(PDOS)。图3可以看出Ti3(ZnxAl1-x)C2固溶体体系的态密度分布情况。Ti3(ZnxAl1-x)C2(x=0)的TDOS图可分为4个主峰，随着Zn原子掺杂浓度的增加，TDOS图逐渐出现第五个峰。其中在导带中只有一个峰PⅠ，而在价带中有PⅡ、PⅢ和PⅣ三个峰。当有Zn原子掺杂时出现第五个峰PⅤ，其中在-12.4～-8.2 eV能量区间出现的PⅡ主要来自C原子2s轨道电子的贡献，少部分来自Ti原子3d轨道电子；在-5.9～-1.7 eV能量区间出现的PⅢ峰主要来自Ti原子3d轨道电子、Al原子3p轨道电子和C原子2p轨道电子的杂化作用。但随着Zn原子掺杂比例的增加，Al原子3p轨道电子的贡献在逐渐降低，这表明Ti原子和C原子之间结合成键具有很强的共价键，从而导致了该固溶体的结构模型是稳定的；在价带顶-1.7～0 eV能量区间出现的PⅣ主要是来自Ti原子3d轨道电子和Al轨道电子3p的杂化作用；在位于导带0～4.2 eV能量区间出现的PⅣ峰主要来自Ti原子3d轨道电子的贡献，而Al原子3p轨道电子和C原子2p轨道电子的贡献相对非常少；在Zn原子的掺杂下，-7.4～-6 eV能量区间出现的PⅤ峰几乎都是来自Zn原子3d轨道电子的贡献，其能量值与Zn原子掺杂浓度成正比。该固溶体费米面的位置是在0 eV能量值处，其电子态密度计算值N(EF)都大于0，主要来自Ti原子3d轨道电子的贡献，表明电子较容易得到能量跃迁到导带，从而有像金属一样的导电特性，呈金属性。同时随着掺杂Zn原子浓度的增加，费米面偏移向了更高能级区域，使得在费米能级处的电子态密度值逐渐增大，Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶体其值依次为16.65 eV、19.09 eV、20.86 eV、22.65 eV、23.06 eV，其导电性能也在依次增强，其中Ti3ZnC2的导电性能是最强的。

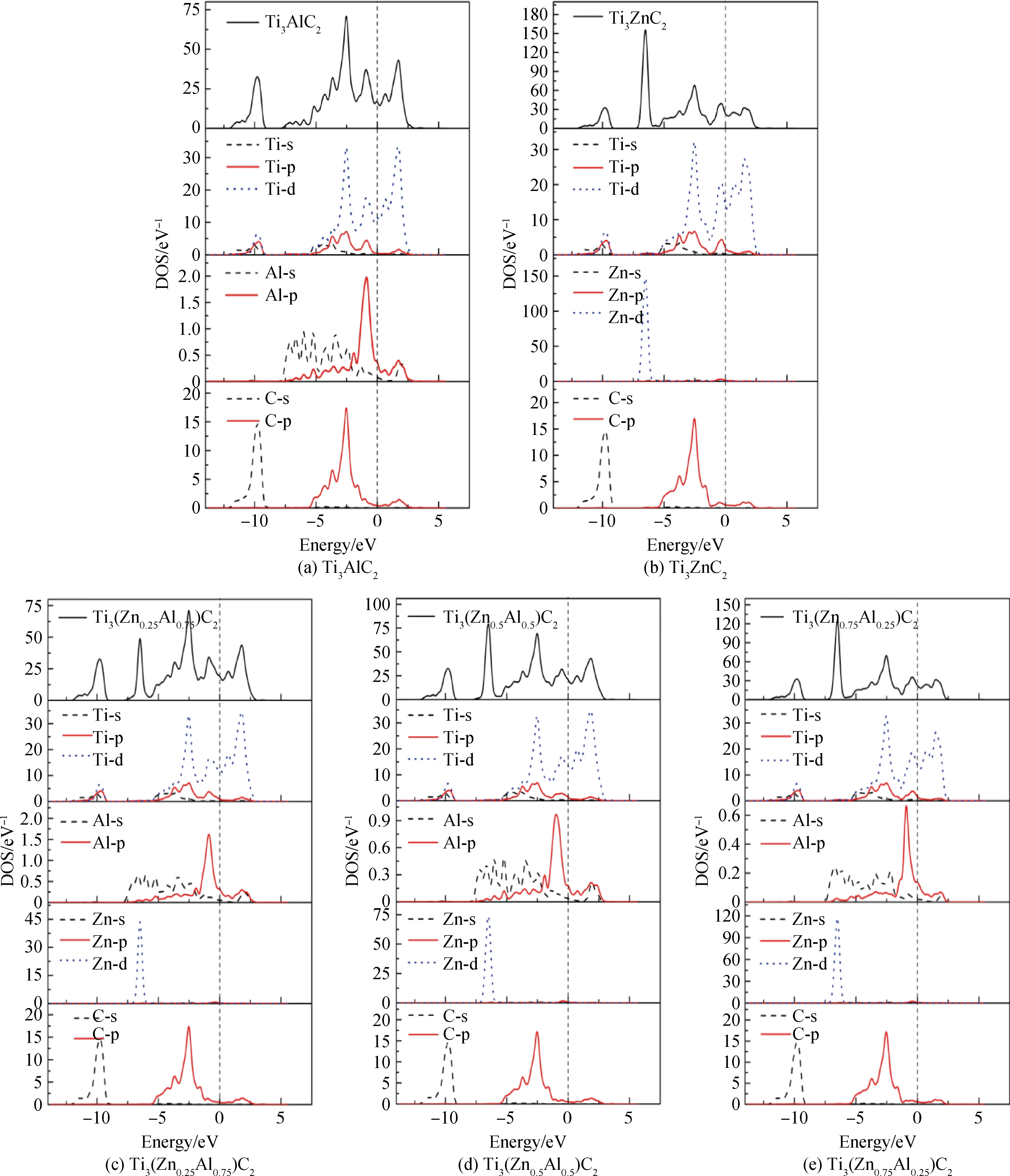
图3 Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶体的总态密度(TDOS)和分波态密度(PDOS)图Fig.3 Calculated total DOS and PDOS of Ti3(ZnxAl1-x)C2 (x=0, 0.25, 0.5, 0.75, 1) solid solutions

为了得到Ti3(ZnxAl1-x)C2固溶体更加详尽的化学键情况，计算了该固溶体的电子局域函数(ELF)，并选取各个晶胞(110)面进行分析。图4可以看出，在Ti和C原子之间的电子局域函数更倾向于C原子，这也说明了C原子易得到电子而Ti原子易失去电子，从而表明Ti—C键之间是强共价键和离子键的结合，使其具有陶瓷材料的高强度、高模量和高熔点。在Ti和Zn原子以及Ti和Al原子的中间，它的电子局域函数接近于0.5，这说明Ti—Zn和Ti—Al键是具有金属键特性的。同时可以看出其具备共价键和金属键成分，这使得该固溶体具有金属材料的延展性和导电性。

图4 Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶体的电子局域函数Fig.4 Electronic local area functions of Ti3(ZnxAl1-x)C2 (x=0, 0.25, 0.5, 0.75, 1) solid solutions

通过VASP计算和VTST的脚本处理得到的Bader电荷，能够更加详细地分析电子的转移情况，表2可以看出各个原子得失电子的情况。Ti原子失去电子使其带正电荷，并且由于Ti1和Ti2原子在结构中的位置不同，这导致失去电子的数量也会有差别；Al和Zn原子以及C原子得到电子使其带负电荷，因此，Ti3(ZnxAl1-x)C(x=0, 0.25, 0.5, 0.75, 1)固溶体均具有共价键和离子键以及金属键的综合特性。还看到Ti和C的总Bader电荷几乎是恒定的。Al和Zn的总Bader电荷从28.904增加到101.416，这说明随着Zn原子掺杂浓度的增加，Zn原子得到的电子随之增加，导致了总电子数也随之增加，这对Ti3(ZnxAl1-x)C2固溶体体系的晶格参数有本质的影响。

表2 Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶体的Bader电荷分析Table 2 Bader charge analysis of Ti3(ZnxAl1-x)C2 (x=0, 0.25, 0.5, 0.75, 1) solid solutions

2.2 弹性性质

在优化后的晶胞结构的基础上，进一步研究了Ti3(ZnxAl1-x)C2固溶体体系的力学特性，通过VASP计算得到该材料的弹性常数和弹性模量分别列在表3中，根据Born和Huang力学稳定性判据[26]对该六方晶系的五个独立的弹性常数(C11、C33、C44、C12、C13)列出以下稳定性条件：

(2)

由表3可知，Ti3(ZnxAl1-x)C2固溶体体系均满足稳定性条件，可以证明Ti3(ZnxAl1-x)C2固溶体均是力学稳定性材料。

利用弹性常数可以研究具有六方晶体结构的Ti3(ZnxAl1-x)C2固溶体体系的弹性各向异性[27]，普遍使用以下三个参数来进行判定：

(3)

式中：ΔP表示材料压缩波的各向异性情况，而ΔS1和ΔS2表示材料剪切波的各向异性情况。当它们得出的参数值都不为1时，该材料的弹性是各向异性的。从表3可知该材料均表现为各向异性的情况。其中弹性常数C11和C33远高于C44，这说明该固溶体的单向变形阻力远高于剪切变形阻力。采用Vogit-Reuss-Hill近似计算得到体模量(B)、剪切模量(G)和杨氏模量(E)等。其中体模量是衡量材料抵抗体积变化的能力，是抵抗断裂的能力；剪切模量是衡量材料抵抗形状变化的能力，是抵抗塑性变形的能力。这两个模量的比值(G/B)是Pugh提出的一个经验判据，可以用来预测材料的脆韧性[28]。从表3中可以看出其值都大于0.57，预示着Ti3(ZnxAl1-x)C固溶体体系都为脆性。除此之外，泊松比σ作为衡量脆韧性的另一个判据，其值均小于1/3，说明了其都为脆性，这与G/B经验判据的结论一致。但随着掺杂Zn原子浓度的增加，G/B逐渐接近于经验判据中韧塑性的临界值,这表明了该固溶体的韧性有逐步增强的趋势。

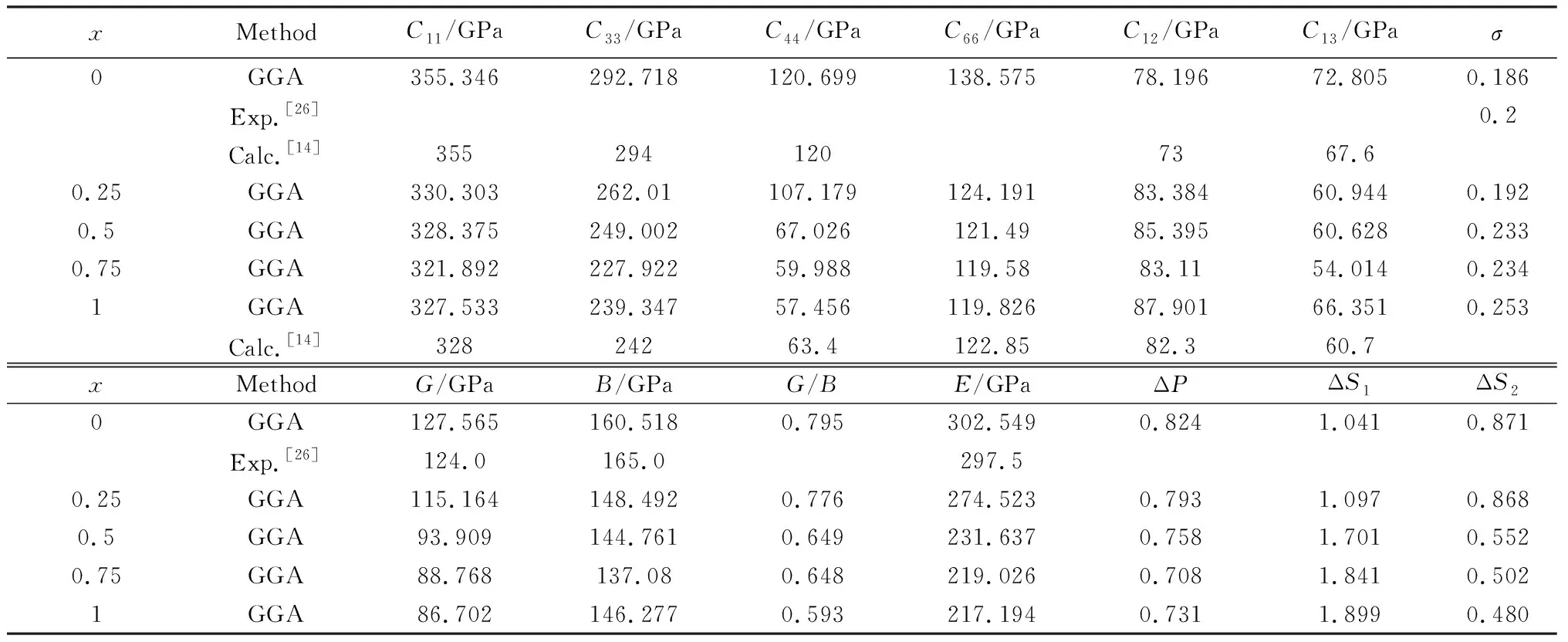
表3 Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶体的各向异性参数(ΔP、ΔS1、ΔS2)，弹性常数Cij和弹性模量Table 3 Anisotropy parameters (ΔP, ΔS1, ΔS2)， calculated elastic constants Cij and elastic moduli for Ti3(ZnxAl1-x)C2 (x=0, 0.25, 0.5, 0.75, 1) solid solutions

3 结 论

本文采用基于密度泛函理论的投影缀加平面波方法，系统地对Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶体体系进行VASP模拟理论计算和性质分析。通过研究表明：计算得到的形成焓均小于零，符合热力学稳定；结合声子色散关系图，可知其均具有本征值稳定性，符合动力学稳定；根据弹性常数满足Born稳定判据，符合力学稳定。对于电子结构性质，费米能级处电子态密度值N(EF)均大于0，主要来自Ti原子3d轨道电子的贡献，表明该材料均具有导电能力，呈金属性。同时随着掺杂Zn原子浓度的增加，费米面偏移向了更高能级区域，使得在费米能级处的电子态密度值逐渐增大，这使得导电性能也在依次增强，其中Ti3ZnC2的导电性能是最强的。在电子局域函数图和Bader电荷的结合下，可以得到该材料均具有共价键和离子键以及金属键的综合特性。对于弹性性质，分析得出其弹性均是各向异性的，并且该固溶体各浓度下均为脆性。但随着掺杂Zn原子浓度的增加，G/B逐渐接近于经验判据中韧塑性的临界值,表明该固溶体的韧性有逐步增强趋势。本文研究了Ti3(ZnxAl1-x)C2(x=0, 0.25, 0.5, 0.75, 1)固溶体体系主要的物理性质，这一系列的研究结果希望能为今后的实验和理论研究提供参考。