基于SOA优化模糊PID的水肥控制系统研究*＊

2022-04-13崔迎港徐晓辉宋涛孙圆龙司玉龙

中国农机化学报 2022年3期

崔迎港，徐晓辉，宋涛，孙圆龙，司玉龙

(河北工业大学电子信息工程学院，天津市，300401)

0 引言

水肥一体化技术是一种新型的水肥灌施技术，该技术采用以水带肥、水肥同施的方式作业，具有节水节肥、省工增效的特点[1]。然而水肥一体化灌施过程中存在非线性、大惯性和时滞性等问题，影响着系统的混肥效果、精度及运行效率[2]。因此，开展以水肥一体化为主体的灌施技术研究，是促进我国农业由传统化向精细化发展的重要举措。

针对目前水肥控制系统存在的问题，吕途等[3]设计了水肥的模糊控制器，提升了系统的精度及调节能力。Lepeng Song等[4]采用模糊PID控制策略设计了变量肥液系统，提升反参数变化的鲁棒性及控制精度。Abioye等[5]认为先进智能控制策略是解决灌施精度与效率的可行方案之一。Supriya Jaiswal等[6]基于模糊推理机制设计了灌施控制器，有效提升了水肥利用率。在目前的研究中，虽然模糊、PID等控制器能提升水肥控制系统性能，但其中的参数仍需凭经验调节，自适应能力欠佳、抗干扰能力较差[7]。

针对上述模型中的不足，设计一种SOA优化模糊PID的水肥控制系统。系统采用具有自适应特性的SOA算法，凭借其优异的寻优能力和收敛速率，对模糊控制器的量化因子、比例因子参数进行智能优化整定。通过仿真对比实验及实际系统搭建，分析优化后的系统精度、稳态性及自适应能力。

1 系统结构组成及硬件设计

1.1 系统结构组成

水肥控制系统结构如图1扬示，系统主要由人机交互模块、数据采集模块、输出控制模块及液罐管路四部分组成。人机交互模块由主控制器、触摸屏组成，可根据用户设定由主控板向下传输控制信号，实现对水肥浓度的实时调控。数据采集模块由流量、压力、电导率EC(Electric Conductivity)传感器、开发板等组成，该模块可实时检测管道水力信息，通过TCP/IP协议向主控制器传输数据。

图1 水肥控制系统结构图Fig.1 Structure diagram of water and fertilizer control system

输出控制模块主要由调频增压泵、吸水泵、恒压阀、电磁阀等设备组成，当调频增压泵接收到主控制器传输的控制信号后，对管路肥液流动状态进行调整，完成对其浓度调控。液罐管路包含了文丘里管组、肥液罐、混合罐等设备，混合后的溶液储存在混合罐中，供田间管网灌施。

1.2 硬件系统设计

在水肥控制系统的硬件设计中，人机交互模块的主控制器以目前市场上主流的高性能Arm SoC(瑞芯微RK3399)为核心，搭载Linux集成开发环境，可实现控制算法移植、硬件驱动编程、用户界面(Graphical User Interface)的开发。同时，系统配备了将串口数据转化为IP数据的4G-DTU(Data Transfer Unit)模块，可实现主控制器与云端数据库的连接。

数据采集模块选用RK3228H开发板，其搭载ESP系列WIFI芯片，便于实现数据无线传输。模块中电导率EC传感器选用工业级CM-230B，测量范围为0～10mS/cm，精度等级为1%(FS)，满足水肥溶液电导率检测精度需求。霍尔流量计选用MJHZ21WB，测量范围为1～30 L/min，其输出的脉冲信号可通过霍尔流量曲线转换为流量数据。压力变送器选用MIK-P300，其量程大小为-0.1～60 MPa，输出的4～20 mA模拟信号通过A/D转化模块PCF8591实现压力数据采集。数据采集模块中的电路原理图如图2扬示。

图2 数据采集模块电路原理图Fig.2 Circuit schematic diagram of data acquisition module

2 水肥模糊PID控制模型

2.1 水肥控制模型

水肥控制系统中的调频增压泵是一种水压可调的稳压供水设备，其压力上升过程为典型一阶惯性环节，稳压过程是纯时滞环节。水泵的系统模型

式中：I1——供水过程中水泵的转速，r/min；

P1——出口压力，MPa；

T1——水泵供水的惯性时间常数，s；

k1——系统增益；

τ1——供水泵稳压过程的时滞常数，s。

在水肥溶液制备的过程中，文丘里吸肥管组及主水管路液体运移存在一定的时间滞后，因此该过程是一个延时为τ2的一阶惯性环节，其模型

式中：e1——系统设定的水肥溶液EC值，mS/cm；

q1——溶液制备过程中的母液流量，L/min；

T2——溶液制备过程的惯性时间常数，s；

k2——制备过程的系统增益；

τ2——时滞常数，包含抽取母液及水肥管路液体流动时延，s。

根据水泵模型参数和系统辨识[8-10]，可以确定该水肥控制系统为上述环节的串级惯性滞后系统，其模型如式(3)扬示。

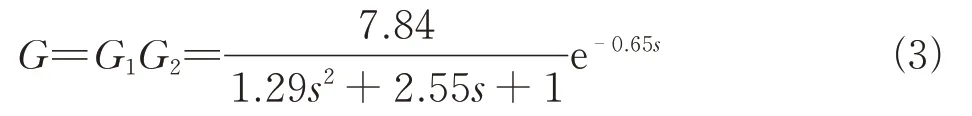
2.2 模糊PID控制原理

模糊PID控制器包含模糊控制与PID控制两个部分。

模糊控制器是根据专家在实际系统调控中总结出的经验规律制定成模糊规则表，实现由操作经验的语言表述转化至硬件系统的控制领域应用[11]。

PID（Proportion Integral Differential）是工业控制领域常用的控制算法，其控制器输出值计算方式如式(4)扬示。

式中：u(t)——控制器输出值；

e(t)——预设与输出的控制偏差；

kp——比例系数；

ki——积分系数；

kd——微分系数。

在控制过程中，比例系数kp能够成比例减小系统的偏差，积分系数ki能够消除系统收敛过程中随时间变化产生的偏差累计量，微分系数kd能够减小偏差变化率，但是上述参数设置不佳时，均会导致系统超调和振荡，无法达到收敛。

对于存在非线性及时滞性的水肥控制系统来说，使用传统PID控制效果较差，需与模糊控制结合，提升系统控制性能。

在水肥模糊PID控制中，设计的模糊PID的控制器框图如图3扬示，控制过程如下：

图3 模糊PID控制框图Fig.3 Fuzzy PID control block diagram

1）控制器将系统预设电导率与传感器实测值进行比对，得到误差E(k)及误差变化率Ec(k)；

2）E(k)和Ec(k)经过量化因子Ke、Kec计算后，转化为模糊量；

3）模糊量根据制定的模糊规则表进行推理计算，得到三个模糊解；

4）模糊解通过比例因子K1、K2、K3，输出系数增量Δkp、Δki、Δkd，完成对PID控制器参数调控。

2.3 水肥模糊PID控制模型

基于传统水肥控制系统，模糊控制器的模糊语言变量设定为7个，即{NB(负大)，NM(负中)，NS(负小)，ZO(零)，PS(正小)，PM（正中)，PB(正大)}[12]。输入的隶属度函数为三角形，模糊子集论域为{-3,3}，输出隶属度函数为高斯-三角混合型，模糊子集论域为{-3,3}。模糊控制器输入输出变量的隶属度函数如图4和图5扬示。

图4 输入变量隶属度函数图Fig.4 Membership function diagram of input variables

图5 输出变量隶属度函数图Fig.5 Membership function diagram of output variables

根据农业专家对制备水肥溶液的调控经验及PID控制器参数调整机制[14]，可得如下控制规则：

1）当|E|较大时，表示水肥溶液EC值偏差较大，此时应提高Δkp，并减小Δki、Δkd，加快系统收敛过程；

2）当|E|、|EC|适中时，表示水肥溶液EC值正向预设值靠近，此时应减小Δkp，Δki、Δkd取值适中，使系统保持稳定状态，平缓调控至预设目标；

3）当|E|较小时，表示水肥溶液EC值接近预设值，此时应提高Δkp、Δki，提升系统容错能力，Δkd取值适中，减小系统振荡；

4）当|EC|较大时，比例系数过高易使得系统产生振荡，此时应减小Δkp，Δkd取较小值；

5）当|EC|较小时，系统响应缓慢，此时应增大Δkp，Δki取较小值。

3 SOA优化模糊PID水肥控制器设计

人群搜索算法(SOA,Seeker Optimization Algorithm)是一种新型群体智能进化算法，其可通过模拟人对空间中位置和方向的搜索行为，寻找目标最优解[14]。

在传统的模糊PID控制中，量化因子和比例因子需根据专家经验设定，设定后无法自适应调整[15]。这些参数的设置不佳会导致系统易产生振荡和超调，无法适应实际水肥调控中存在的随机误差及扰动等情况，稳态性能较差。为提高模糊PID控制器的性能，采用SOA智能算法对模糊控制器的输入输出过程进行优化，其结构如图6扬示。

图6 SOA优化模糊PID的控制框图Fig.6 Control block diagram of SOA optimized fuzzy PID

3.1 标准SOA算法

SOA(Seeker optimization algorithm)是一种新型群体智能进化算法，其基本原理是:假设一个群体有S位搜索个体，分布在D维空间中，每位个体被赋予位置和方向信息，通过多次搜索更新，使个体在空间中获取最优位置和方向，得到目标的最优解。个体Xi扬处的位置如式(5)扬示。

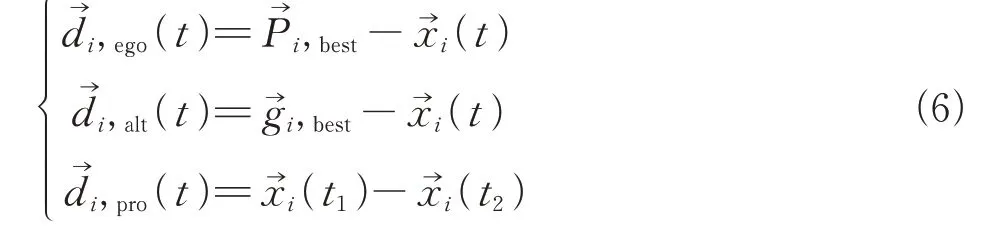
——个体历史最佳位置；

——邻域内群体最佳位置；

——以当前时刻为基准前一时刻和前两时刻最佳位置。

当计算出个体三种搜索行为后，便可根据个体最终搜索方向进行位置的迭代更新

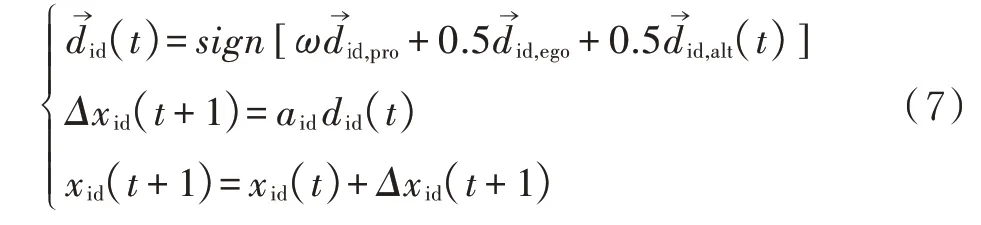
式中：ω——惯性权重，决定个体下一时刻的利己移动方向；

——个体下一时刻搜索方向；

aid——由高斯隶属度函数确定的搜索步长；

xid(t+1)——个体下一时刻扬在位置。

为评价搜索进化过程中解的优劣，选用ITAE性能指标作为最小目标函数，其中增加输入平方项u2(t)来减小系统的超调和振荡，具体适应度函数

其中：ω1取0.9，ω2取0.1。

3.2 惯性权重自适应

在SOA算法中，惯性权重对个体的搜索方向起着重要作用。当个体的目标值趋于一致时，个体搜索能力较差，应增加惯性权重，提高全局搜索能力；当个体搜索值较分散时，应减小权重加快收敛。然而在标准SOA中，惯性权重ω一般为固定值，这种策略将无法应对模糊控制的随机干扰因素。因此需采用具有自适应特性的权重因子进行寻优

式中：ωmax——惯性权重最大值；

ωmin——惯性权重最小值；

f——当前目标适应度值；

fmin——当前群体个体中适应度最小值；

favg——当前群体个体中适应度平均值。

当计算出的适应度比群体均值低时，选用自适应权重ω进行迭代，否则选用ωmax进行迭代，使个体迭代权重可根据群体适应度值的变化自适应调整。

3.3 SOA优化模糊PID控制器设计

基于上述研究，设计一种SOA优化模糊PID的水肥控制器，具体步骤为：

1)初始化搜索群体，设置SOA个体规模N为50，个体搜索空间维数D为5，代表模糊控制的量化因子及比例因子，个体搜索范围为[0,5]，最大迭代次数M为50次，最小适应度值f为0.1，惯性权重ωmax、ωmin分别为0.9、0.1；

2)调用水肥模糊PID模块，获取当前迭代过程中每位个体的适应度值，判断是否满足中止条件(达到最大迭代次数或最小适应度值)；

3)计算当前迭代中种群适应度的最值与均值，根据公式(9)分别对N位个体赋予自适应惯性权重ω；

4)根据公式(7)更新个体的方向与位置，并转回步骤2。

SOA优化模糊PID的水肥控制流程如图7扬示。

图7 SOA优化模糊PID的水肥控制流程Fig.7 Water and fertilizer control flow based on SOA optimized fuzzy PID

根据上述优化步骤，采用式(3)水肥控制模型进行参数寻优，个体寻优过程及适应度曲线如图8、图9扬示。

图8 量化因子、比例因子优化曲线Fig.8 Optimization curve of quantization factor and scale factor

图9 最优个体适应度变化曲线Fig.9 Curve of the best individual fitness

由图8、图9可知，SOA优化模糊PID在35次迭代后达到最优，量化因子、比例因子数值不再变化，目标适应度值从2.01下降至1.37，寻优效果显著。经过优化后的模糊控制器参数值分别为：ke=3.039，kec=0.130，k1=3.912，k2=0.35，k3=4.072。

4 仿真分析及系统测试

4.1 仿真平台搭建及结果分析

Simulink是一个动态系统建模、仿真和综合分析的平台，具有结构清晰、仿真精细、贴近实际等优点，在控制理论研究中得到了广泛应用[17]。为了分析SOA优化模糊PID水肥控制模型的性能，通过Simulink进行仿真对比实验，基于Simulink平台搭建的水肥控制模块如图10扬示。

图10 SOA优化模糊PID的水肥控制模型Fig.10 Water and fertilizer control model based on SOA optimized fuzzy PID

在该模型中设置系统输入为一阶阶跃响应，模拟水肥电导率的预设值。传统PID、模糊PID、SOA优化模糊PID三种控制方法的系统响应曲线如图11扬示。

图11 水肥控制模型响应曲线Fig.11 Response curve of water and fertilizer control model

根据图11的响应曲线可得，将传统PID应用到水肥控制系统时，上升过程较快，最先到达预设值，但由于被控对象具有非线性，易产生超调，最终超调量为13.7%，调节时间为46.3 s，稳态误差为0.5%，系统性能及稳态性较差。模糊PID模型的超调量为3.7%，调节时间为26.2 s。该模型虽可有效抑制超调，但其上升过程较慢，控制器中的参数仍需凭经验调节，自适应能力欠佳。基于SOA优化模糊PID的模型控制过程中未出现超调，相较于模糊PID，超调量减小了3.7%，调节时间缩短了26.7%，其控制性能最佳。三种控制方法具体的性能指标如表1扬示。

表1 控制系统各项性能指标对比Tab.1 Contrast of various performance indicators of control system

为验证SOA优化模糊PID水肥控制模型的稳定性及自适应能力，分别引入干扰信号及高斯随机信号模拟实际环境参数变化后的响应实验。图12扬示为三种控制系统的输出稳定后，第80 s引入干扰的阶跃响应曲线。

图12 引入干扰的系统阶跃响应曲线Fig.12 Step response curve of the system with interference

由图12可得，在引入预设值8%的扰动量后，SOA优化模糊PID控制器在10 s后回到稳态，而模糊PID与传统PID分别在20 s和27 s后回到稳态。

图13扬示为引入高斯随机信号后三种控制方法的系统输出曲线，其中信号的均值中心设为1，方差设为0.1，采样时间为25 s。由图13可得，在引入高斯随机信号后，SOA优化模糊PID控制器的调节能力强，曲线追踪效果好，稳态性强，其系统响应性能明显优于模糊PID与传统PID。

图13 引入随机信号的系统输出曲线Fig.13 Step response curve of system with high frequency signal

4.2 系统测试

为验证系统实际测试效果，进行单路肥路流量控制试验。系统将控制算法移植到RK3399主控板，通过编译生成动态库后供实时调用[18]。在实验室环境下搭建的水肥控制系统如图14扬示，测试过程中主管路压力为0.28 MPa，主管路流量为18.3 L/min，目标EC值设定为2.0 mS/cm，由于实测过程中存在随机信号干扰及流体扰动等情况，故EC值处于稳定波动时认为达到稳态，基于不同控制模型下的EC试验结果对比如表2扬示。由表2可知，传统PID控制的EC值在稳态时波动幅度达到0.33 mS/cm，精度最差，模糊PID控制次之。相比之下，经SOA优化后的模糊PID控制模型EC稳态波动幅度仅为0.06 mS/cm，控制精度最佳，超调量仅为1.5%，能够在减小超调的情况下最先调节至稳态，稳态性能最优，实际混肥效果显著。