高三数学综合测试
2022-04-11
一、单项选择题(本大题共8小题,每小题5分,计40分)
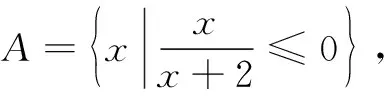
(A) {x|x≥-2} (B) {x|x>-2}
(C) {x|x≥0} (D) {x|x>0}
2.若l,m为两条不同的直线,α为平面,且l⊥α,则“m⊥l”是“m∥α”的( )
(A) 充分不必要条件
(B) 必要不充分条件
(C) 充要条件
(D) 既不充分也不必要条件
3.若0 (A)x (C)z (A) 12 (B(-12 (C) 6 (D)-6 5.已知(1+2x)n的展开式中第4项与第6项的二项式系数相等,则(1+2x)n的展开式的各项系数之和为( ) (A) 38(B) 310(C) 28(D) 210 (A)9 (B) 8 (C) 6 (D) 10 7.如图是长方体的展开图,且AD=2AB,ABFE为正方形,其中P,Q分别为AD,HI的中点.下列判断①AM∥CG,②AF∥DK,③BP∥JQ,④BP⊥QJ中,正确判断的个数为( ) (A)0 (B) 1 (C) 2 (D) 3 8.已知函数f(x)=xex-x-lnx+1-m有两个不同的零点,则实数m的取值范围是( ) (A) (-∞,1) (B) (-∞,2) (C) (1,+∞) (D) (2,+∞) 二、多项选择题(本题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分) 9.下列命题中正确的有( ) (B) 若复数z满足z2∈R,则z∈R (A) π是函数f(x)的一个周期 11.已知正数a,b满足(a-1)b=1,则( ) (A)a+b≥3 (C) 2log2a+log2b≥2 (D)a2+b2>2a (A)k1k2=-a2 (D)∆PAB的面积随k1的增大而减小 三、填空题(本大题共4小题,每小题5分,计20分) 13.已知直线l1:ax+2y-3=0与l2:3x+(1-a)y+4=0,若l1⊥l2,则实数a的值为______. 14.已知数列{an}的前n项和为Sn,a1=1,a2=2,an+2=an+1-an,则S2019=______. 四、解答题(本大题共6小题,计70分.解答时应写出文字说明、证明过程或演算步骤) 17.(本小题满分1分)已知盒中有形状大小都相同的3个黑球和10个白球,每次从中取1个球,取到黑球记1分,取到白球记2分,有放回地抽取3次,用随机变量ξ表示取3次所得的分数之和.试求: (1)3次都取到黑球的概率; (2)随机变量ξ的分布列. 18.(本小题满分12分)在①a1+a3=6,S9=81,②Sn=n2+k(k为常数)这二个条件中任选一个,补充在下面的问题中并解答. 问题:已知等差数列{an}的前n项和为Sn,且______. (1)求数列{an}的通项公式; 19.(本小题满分12分)在平面四边形ABCD中,∠ABD=∠BCD=90°,∠DAB=45°. (1)若AB=2,∠DBC=30°,求AC的长; 20.(本小题满分12分)给出两块相同的正三角形铁皮(如图1,图2). (1)要求用其中一块剪拼成一个三棱锥模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的面积相等. ① 请设计一种剪拼方法,分别用虚线标示在图1、图2中,并作简要说明; ② 试比较你剪拼的正三棱锥与正三棱柱的体积的大小. (2)设正三角形铁皮的边长为a,将正三角形铁皮的三个角切去三个全等的四边形,再把它的边沿虚线折起(如图3),做成一个无盖的正三角形底铁皮箱,当箱底边长为多少时,箱子容积最大?最大容积是多少? (1)求椭圆C的方程; (2)若f(x)有两个极值点x1,x2(x1 参考答案 一、单项选择题 1. B;2. B;3. A;4. D;5. A; 6. A;7. C;8. D. 二、多项选择题 9. AD;10. ACD; 11. ACD;12. BCD. 三、填空题 13.-2;14.4;15.② ③ ④; 四、解答题 (2)ξ的取值是3,4,5,6. ξ3456 P27642764964164 18.设等差数列{an}的公差为d,d>0. 选条件①: 所an=a1+(n-1)d=2n-1,n∈N*. 因为t≤15,所以(2m-1)2≤87.又m∈N*,所以2m-1≤9,得m≤5. 选条件②: 因为t≤15,所以(2m-1)2≤87.又m∈N*,所以2m-1≤9,所以m≤5. (2)在Rt∆BCD中,设∠DBC=α,则BC=BDcosα=2cosα. 20.(1)① 如图1,沿正三角形三边中点连线折起,可拼得一个正三棱锥. ② 依上面剪拼方法,有V柱>V锥. 令φ(x)=-ex+e,则φ′(x)=-ex<0,即g′(x)为单调减函数.又g′(1)=0,故当x≤1时,g′(x)≥0;x>1时,g′(x)<0.所以g(x)的单调增区间为(-∞,1),单调减区间为(1,+∞). (2)因为f′(x)=ex(-aex+x),依题意可知f′(x)=0有两个不等实根,即aex=x有两个不等实根x1,x2. 设函数h(t)=(3-t)et-2t-3(t<0),则h′(t)=(2-t)et-2(t<0),h″(t)=(1-t)et>0,易知h′(t)在t<0单调增,即h′(t) 综上,原不等式x1+2x2>3得证.