一道有关四面体体积的世界名题

屈大海 陈沙沙 胡廷佳

(贵州省遵义市第五十四中学,563102)

有关求四面体的体积,数学家们一开始是对其施以割补之术,想将之拼凑成立方体,再从立方体的体积公式导出四面体的体积公式.数学家们为此奋斗了两千多年都没有成功.德裔美籍数学家马克思·德恩于1901年证明了“只根据合同公理证明等底等高的四面体有相等之体积是不可能的.特别是正四面体不能分割成许多块,重新拼凑成立方体.”这就彻底否定了通过割补法求四面体体积公式的途径,探求四面体的体积成为了一道千年难题.

其实,两千多年前,善于用实验发现真理的阿基米德,用装沙子的方法发现四面体的体积是同底等高的三棱柱体积的三分之一,并且用无限逼近的方法证明了他的发现.这种证明方法在现行中学教材中很少出现,笔者经过研究找到了相应解决方法,现整理成文,与大家分享.

在证明四面体的体积公式之前,首先给出n个正整数的平方和公式.设i∈N*,对i=1,2,…,n,有(i+1)3-i3=3i2+3i+1.将这n个等式相加,得(n+1)3-13=3(12+22+…+n2)+3(1+2+…+n)+n,整理可得

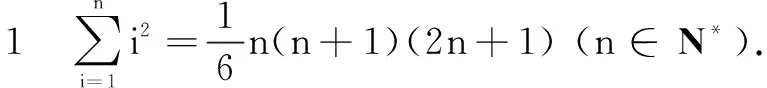
其次,我们再介绍高等数学中的一个重要结论：

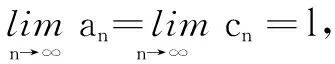
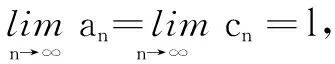
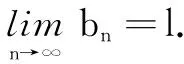
有了上面的知识储备,现在我们可以求四面体的体积了.