2011年北大题

单 墫

(南京师范大学数学科学学院，210023)

我喜欢做大轴题，即最后一题.(有人称之为压轴题，其实不通.压轴题倒数第二，在倒数第一前，最后一题是大轴.没有轴，何来压轴？)

试题(2021年北大第5题)已知圆x2+y2=1上有三个点，坐标分别为(x1,y1),(x2,y2),(x3,y3)，且

x1+x2+x3=0，

①

y1+y2+y3=0.

②

③

证明先考虑一个简单的情况：点(x1,y1)在x轴的正方向上，即x1=1,y1=0.

设x2=cosα,y2=sinα,-π≤α<π；x3=cosβ,y3=sinβ，其中-π≤β<π.则有sinα+sinβ=0.

再考虑一般情况，设i为虚数单位，zj=xj+iyj,j=1,2,3.

则由已知①，②两式，得

z1+z2+z3=0.

④

令zj′=eiθzj(1≤j≤3),并且z1′=1.即将zj旋转同一个角θ，使得z1′成为x1′=1,y1′=0的点.由④式可得

z1′+z2′+z3′=0.

所以x1′+x2′+x3′=0,y1′+y2′+y3′=0.

同前面的证明，可得

⑤

⑥

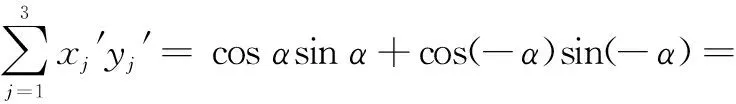
当然，不先做简单情况，直接做一般情况也无不可，但“从简单的做起”，将一般情况化归为简单情况，也是一种趣向，一种爱好.