发现之旅:由正三角形“衍生”出正三角形再探
2016-06-01◎杨川
◎杨 川
(四川新津县邓双学校,四川 新津 611437)
发现之旅:由正三角形“衍生”出正三角形再探
◎杨 川
(四川新津县邓双学校,四川 新津 611437)
在文[1]中探究了由正三角形“衍生”出正三角形的一些情况,现对原正三角形与“衍生”出的正三角形边长、面积之间的联系进行探究.
正三角形;边长;面积
一、命题探究
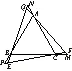
探究命题1 已知,如图1,点M,N,P分别在正三角形ABC(边长为a)的BC,CA,AB的延长线上,且BM=CN=AP=b(b>a),连接NP,PM,MN.
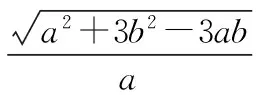
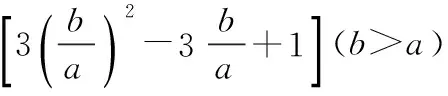
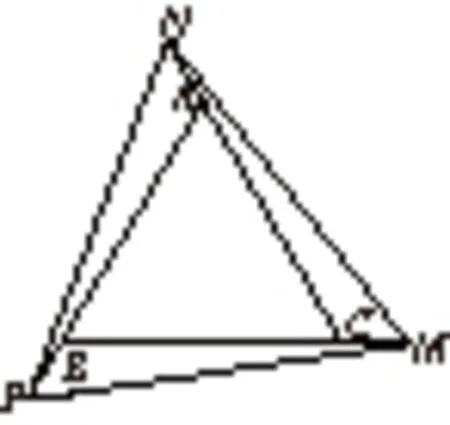
图1
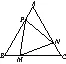
图2
证明① 在文[1]中已证△MNP为正三角形.
∵AB=a,BM=AP=b,∠ABC=60°,
∴BP=b-a,∠PBM=120°,

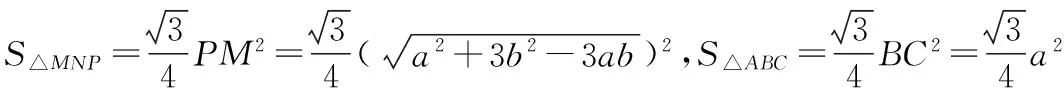
探究命题2 已知,如图2,点M,N,P分别在正三角形ABC(边长为a)的BC,CA,AB的边上,且BM=CN=AP=b(b 证明① 在文[1]中已证△MNP为正三角形. ∵BC=a,BM=CN=b,∠C=60°,∴CM=a-b, 特别的,当点M,N,P为中点时,即b=0.5a,△MNP的面积为△ABC面积的0.25倍. 图3-1 证明① 在文[1]中已证∠BQM=60°,△EFQ为正三角形. ∵在△QBM和△CBN中,∠BQM=∠BCN,∠QBM=∠CBN,∴△QBM∽△CBN, 易证△BMQ≌△CNE(ASA),∴BM=CN,QM=EN, (1) ∴BN2=a2+b2-2a·bcos60°=a2+b2-ab>0, (2) 特别的当b=0时,也满足上述式子,此时△EFQ即为△ABC. 图3-2 ∵EQ=BN-NQ-BE. 特别的当b=a时,也满足上述式子,此时△EFQ即为△ABC. 探究命题4 已知,如图4,点M,N,P分别在正三角形ABC(边长为a)的BC,CA,AB的延长线上,且BM=CN=AP=b(b>a),AM,BN交于点Q,BN,CP交于点E,CP,AM交于点F. 图4 证明① 在文[1]中已证△EFQ为正三角形.由题意可得:BC=a(a>0),BM=AP=b(b>a),∠BCN=60°,∴∠PBC=120°, ∴在△CBP中,CP2=BC2+BP2-2BC·BP·cos∠PBC(余弦定理), ∴CP2=a2+(b-a)2-2a·(b-a)cos120°=a2+b2-ab>0, 易证△BPE≌△CMF(AAS),∴BP=CM=b-a,EP=FM,易证△BCP∽△FCM, (3) (4) 一题多变,抛砖引玉,希望能开阔学生的视野,找到解题的灵感,使类似的问题迎刃而解.有纰漏之处,敬请读者指正. [1]杨川.发现之旅:由正三角形“衍生”出正三角形[J].考试与评价,2016(8). [2]程峰.探究与分点有关的两个三角形面积的比值[J].初中数学教与学,2011(23).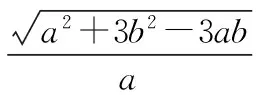
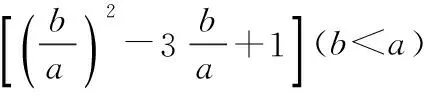
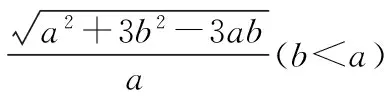
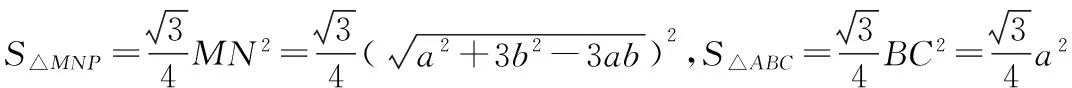
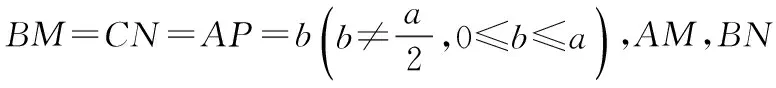
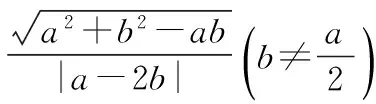
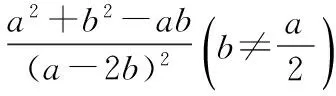
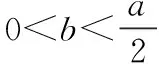
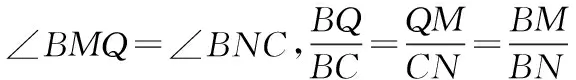
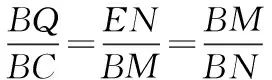
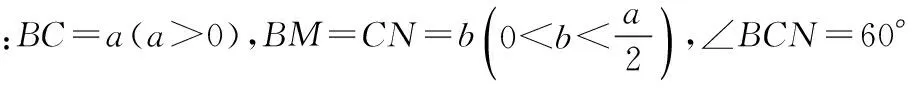
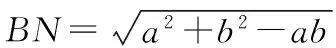
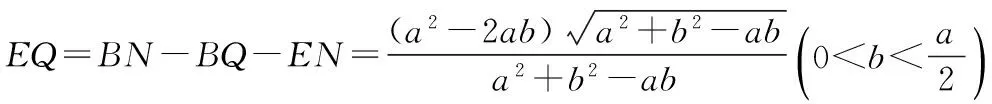
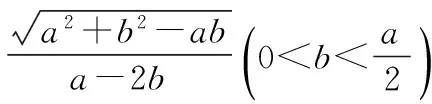
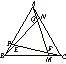
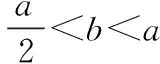
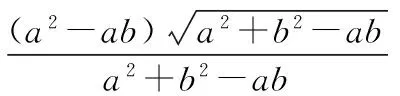
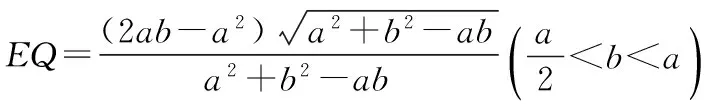
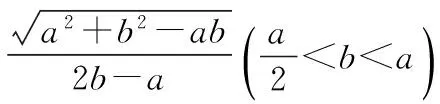
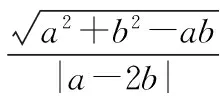
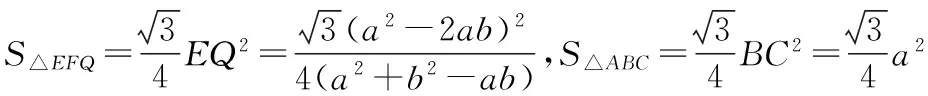
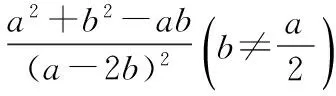
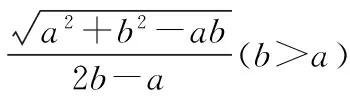
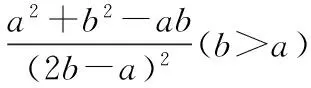
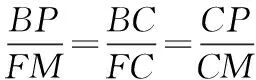
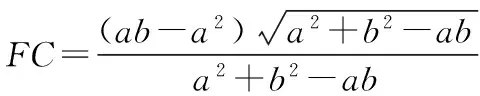
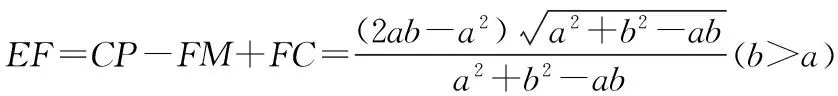
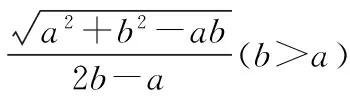

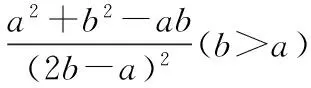
二、结束语
