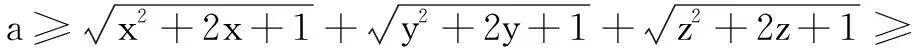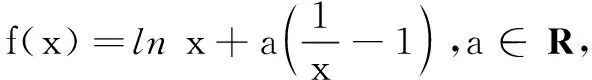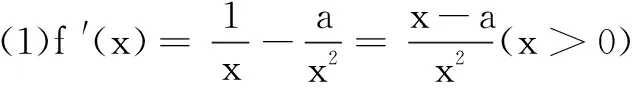活跃在高中数学联赛中的高斯函数

朱小扣

(安徽省无为中学，238300)

高斯函数是高中数学的重要内容和考点,在高中数学竞赛题中频繁出现,且命题灵活,综合度较高,具有一定的难度和挑战性.本文通过对历年来全国各省市竞赛题的分析,总结出以高斯函数为载体的试题命题方向及其解题策略,以期对同学们备战高中数学竞赛有所帮助.

一、几个常用性质

对高斯函数f(x)=[x],下面几个性质在解题时是常用的,需熟练掌握.

(1)f(x)=[x]的定义域为R,值域为Z.

(2)f(x)=[x]的最小正周期为1.

(3)[x]≤x<[x]+1,x-1<[x]≤x.

二、命题规律揭示

1.与二次不等式的融合

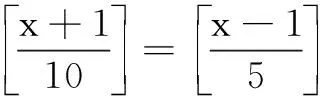
例1(2018年河北省预赛题)规定:对任意x∈R,当且仅当n≤x

2.与方程的融合

例2(2015年天津市预赛题)用[x]表示不超过x的最大整数,方程x2-[x]-2=0的不同实数根共有( )

(A)1个 (B)2个 (C)3个 (D)4个

解由[x]≤x,得x2-x-2≤x2-[x]-2=0,解得-1≤x≤2,故[x]=-1,0,1,2.

综上,选C.

①

将n=-1代入① 式,解得-4≤x<-1;将n=0代入① 式,解得1≤x<6;将n=1代入① 式,解得9≤x<11.故所求的解集是[-4,-1)∪[1,6)∪[9,11).

3.与概率的融合

例4(2018年天津市预赛题)设x为正实数,若[log2x]为偶数,则称x为幸运数.在区间(0,1)中随机选取一个数,它是幸运数的概率为______.

解设[log2x]=2n(n∈Z),则2n≤log2x<2n+1,得22n≤x<22n+1.

4.与格点的融合

例5(2015年江苏预赛题)在平面直角坐标系xOy中,设D是x≥0,y≥0,x+y+[x]+[y]≤19的点(x,y)形成的区域.则区域D中的整点的个数是______.

解由性质(3)及x+y+[x]+[y]≤19,得2[x]+2[y]≤x+y+[x]+[y]≤19,即[x]+[y]≤9.5.

因此,当[x]=0时,[y]可取0,1,2,3,4,5,6,7,8,9,对应10个整点;当[x]=1时,[y]可取0,1,2,3,4,5,6,7,8,对应9个整点;当[x]=2时,[y]可取0,1,2,3,4,5,6,7,对应8个整点;…;当[x]=9时,[y]可取0,对应1个整点.

综上,所求整点共有10+9+8+…+2+1=55个.

5.与权方和等不等式的融合

6.与数列、数学归纳法融合

(1)求a的值;

(2)已知数列{an}满足a1=1,an+1=f(an)+2 (n∈N+),设Sn=[a1]+[a2]+[a3]+…+[an],其中[m]表示不超过m的最大整数.求Sn.

当a≤0时,f′(x)>0,f(x)在(0,+∞)单调增,无最小值,不合题意.

当a>0时,易见f(x)在(0,a)单调减,在(a,+∞)单调增,故f(x)min=f(a)=lna-a+1.

当n=3时,结论已成立.

综上,对一切正整数n≥3,恒有2

所以[a1]=1,[an]=2(n≥2).由此得Sn=[a1]+[a2]+…+[an]=1+2(n-1)=2n-1.

以上介绍了高斯函数与相关知识的六种融合形式.题目是常考常新,但只要大家把握住高斯函数基本性质,就能灵活运用、融会贯通.希望本文能对学生备考联赛有所帮助.