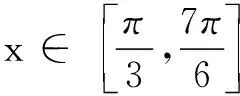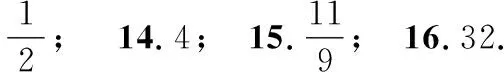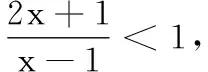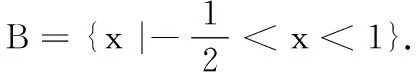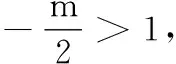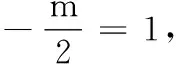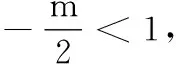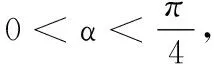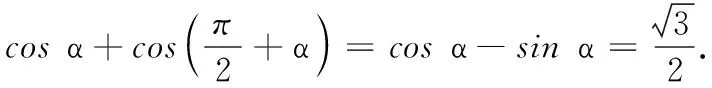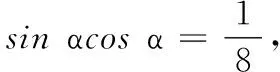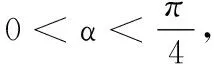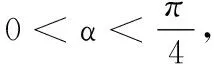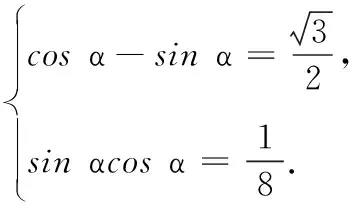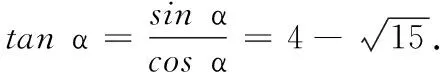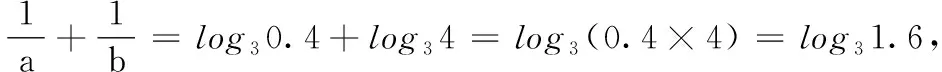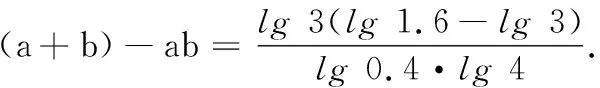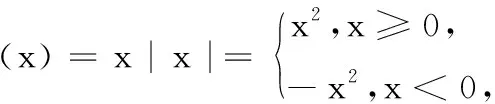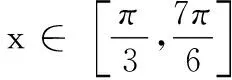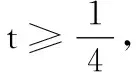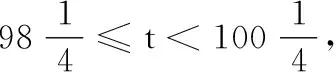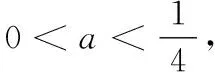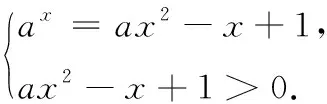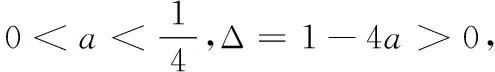高一数学测试
2022-04-11
一、单项选择题(本大题共8小题,每小题5分,计40分)
1.若角α的终边经过点P(3,a)(a≠0),则( )
(A)sinα>0 (B)sinα<0
(C)cosα>0 (D)cosα<0
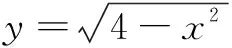
(A)(1,2) (B)(1,2]
(C)(-2,1) (D)[-2,1)
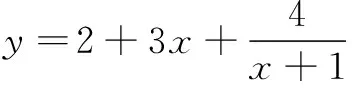
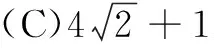
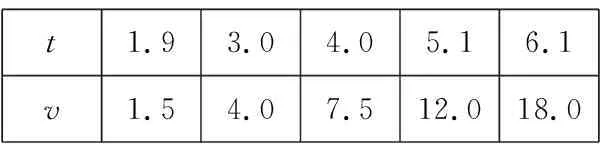
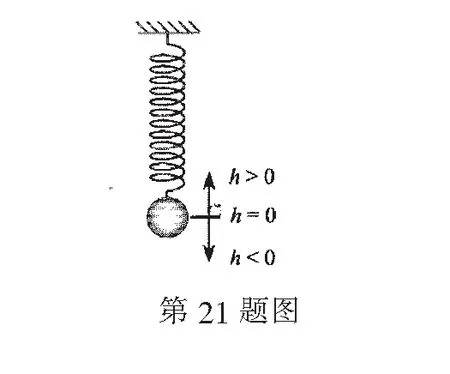
4.已知a,b,m都是负数,且a 5.有一组实验数据如下表所示: t1.93.04.05.16.1v1.54.07.512.018.0 现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是( ) (C)v=log0.5t(D)v=log3t 6.若函数f(x)=sin 2x与g(x)=2cosx都在区间(a,b)上单调递减,则b-a的最大值是( ) 8.若函数f(x)同时满足:① 定义域内存在实数x,使得f(x)f(-x)<0;② 对于定义域内任意x1,x2,当x1≠x2时,恒有(x1-x2)· [f(x1)-f(x2)]>0;则称函数f(x)为“DM函数”.下列函数中是“DM函数”的为( ) (A)f(x)=x3(B)f(x)=sinx (C)f(x)=ex-1(D)f(x)=lnx 二、多项选择题(本大题共4小题,每小题5分,计20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对得5分,部分选对得3分,不选或有选错的得0分) 9.关于函数f(x)=tan 2x,下列说法中正确的是( ) 11.我们知道,如果集合A⊆S,那么S的子集A的补集为sA={x|x∈S,且x∉A}.类似地,对于集合A,B,我们把集合{x|x∈A,且x∉B}叫作集合A与B的差集,记作A-B.据此,下列说法中正确的是( ) (A)若A⊆B,则A-B=∅ (B)若B⊆A,则A-B=A (C)若A∩B=∅,则A-B=A (D)若A∩B=C,则A-B=A-C 12.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号.设x∈R,用[x]表示不超过x的最大整数,y=[x]也被称为“高斯函数”.例如:[-3.5]=-4,[2.1]=2.已知函数f(x)=[x+1]-x,下列说法中正确的是( ) (A)f(x)是周期函数 (B)f(x)的值域是(0,1] (C)f(x)在(0,1)内是增函数 (D)∀x∈R,[f(x)]=0 三、填空题(本大题共4小题,每小题5分,计20分) 16.地震震级是根据地震仪记录的地震波振幅来测定的,一般采用里氏震级标准.震级(M)是用据震中100千米处的标准地震仪所记录的地震波最大振幅值的对数来表示的.里氏震级的计算公式为M=lgA-lgA0,其中A是被测地震的最大振幅,A0是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差).根据该公式可知,7.5级地震的最大振幅是6级地震的最大振幅的______倍(精确到1). 四、解答题(本大题共6小题,计70分.解答时应写出必要的文字说明、证明过程或演算步骤) (1)当m=1时,求A∪B; (2)已知“x∈A”是“x∈B”的必要条件,求实数m的取值范围. (2)求tanα的值. (2)已知a=log0.43,b=log43,求证:ab 20.(本小题满分12分)已知函数f(x)=x|x-a|为R上的奇函数. (1)求实数a的值; (1)求小球相对平衡位置的高度h(单位:cm)和时间t(单位:s)之间的函数关系; (2)小球在t0s内经过最高点的次数恰为50次,求t0的取值范围. 22.(本小题满分12分)对于定义在D上的函数f(x),如果存在实数x0,使得f(x0)=x0,那么称x0是函数f(x)的一个不动点.已知f(x)=ax2+1. (1)当a=-2时,求f(x)的不动点; (2)若函数f(x)有两个不动点x1,x2,且x1<2 ① 求实数a的取值范围; ② 设g(x)=loga[f(x)-x],求证:g(x)在(a,+∞)上至少有两个不动点. 参考答案 一、单项选择题 1.C;2.B;3.A;4.D;5.B; 6.C;7.D;8.A. 二、多项选择题 9.AB;10.BD; 11.ACD;12.AB. 三、填空题 四、解答题 所以A∪B={x|-2 (2)因为“x∈A”是“x∈B”的必要条件,所以B⊆A. 综上,m∈[-2,4]. (cosα-sinα)2 =cos2α-2sinαcosα+sin2α =1-2sinαcosα =5+4+4 =13. (2)解法1因为y=log0.4x在(0,+∞)单调减,y=log4x在(0,+∞)单调增,所以a=log0.43 解法2因为a=log0.43,b=log43,所以 a+b=log0.43+log43 因为lg 3>0,lg 4>0,lg 1.6>0,lg 0.4<0,所以a+b<0. 综上,ab 20.(1)依题意, 由f(-x)=-f(x),可得-x|-x-a|=-x|x-a|对任意x∈R成立, 所以|-x-a|=|x-a|,得a=0. (2)由f(sin2x)+f(t-2cosx)≥0,得f(sin2x)≥-f(t-2cosx),结合f(x)为R上的奇函数,得f(sin2x)≥f(2cosx-t). (注:t0的取值范围不考虑开闭) 22.(1)当a=-2时,f(x)=-2x2+1. (2)① 因为f(x)有两个不动点x1,x2,所以方程f(x)=x,即ax2-x+1=0的两个实数根为x1,x2. 记h(x)=ax-(ax2-x+1),因为h(1)=0,且p(1)=a>0,所以x=1是方程g(x)=x的实数根,即1是g(x)的一个不动点. 综上,g(x)在(a,+∞)上至少有两个不动点.