基于累积绝对位移值的震级估算方法

马美帅，王延伟，汪祚赚，赵庆旭，潘代洪

（1.桂林理工大学广西岩土力学与工程重点实验室，广西 桂林 541004；2.重庆南江工程勘察设计集团有限公司，重庆 401121）

引言

地震是一种无法避免的自然现象，具有极大破坏力，当前科技无法准确地预测地震的发生，而地震预警（EEW）系统被认为是一种减轻地震灾害的有效的方法［1-2］。目前，世界上已有多个国家已经或正在建立地震预警系统，如日本［3］，美国［4］，墨西哥［5］，土耳其［6］，罗马尼亚［7］，意大利［8］，中国［9］等。地震预警系统是在地震发生后，利用先到达的P 波确定地震信息，在破坏性S 波到达前几秒至数十秒向目标区域发出警报，使其能够采取紧急措施，尽量减少地震破坏。震级作为反映地震大小的地震学基本参数，也是关键的地震预警信息，地震预警系统能否快速准确地估算震级是其成败的关键。

地震预警中的震级估算，主要是通过初至P波的预警参数与震级的经验关系来实现的。目前，被广泛研究和应用的预警参数，可以分为三类。一类是与周期有关的参数，这类参数是根据震级越大地震波的周期越长提出的，主要有最大卓越周期τpmax［10］、平均卓越周期τc［11］、平均对数周期τlog［12］和基于小波变化的周期λlog［13］等。另一类是与地震波波形幅值有关的参数，这类参数主要依据震级越大相同震源距测点的地表变形越大，以Wu和Zhao［14］提出的位移幅值Pd的应用和研究最为广泛。还有一类是与地震辐射能量有关的参数，其依据是震级越大地震辐射能量越大，通过对地震波进行积分（求和）来近似求得地震辐射能量，主要有速度平方积分IV2［15］和累积绝对速度值CAV［16］。这三类预警参数都从不同方面代表了初至P 波中与震级相关的信息，与震级相关性越高的预警参数，越有利于震级的估算。为了从前述各预警参数中寻找估算震级准确性最好的参数，多位学者进行了对比分析，结果表明Pd参数与震级有最好的相关性，估算震级的准确性最高［17-22］。此外，多个已建地震预警系统的震级估算方法也主要采用Pd估算震级，例如中国的台湾［23］和福建［24］，日本［25］，美国［26］和伊朗［27］。然而，从信息量上看，Pd参数仅保留了初至P波的最大变形，舍弃了初至P波中与断层破裂过程有关的变形过程信息，并不利于震级的估算，仍有改进的空间。

为了更充分利用初至P波中与震级相关的信息，提高估算震级的准确性，本文提出利用累积绝对位移值（CAD）参数来估算震级。为验证CAD参数的震级估算效果，利用大量的日本强震记录（28018 条竖向记录）的初至3 s ～6 s地震波，分析CAD参数与震级的相关性，以及CAD参数估算震级的误差，并与Pd参数进行对比。结果表明，CAD参数估算震级的准确性高于Pd参数。

1 数据选择及处理

日本Kiban-Kyoshin Net（KiK-Net）台网记录的大量历史强震数据，被广泛应用于地震领域的各项研究。为保证数据规模，从数据库中下载了1997年到2019年的地表地震强震记录，并参考相关研究和地震预警系统的特点，按条件筛选强震记录：震级≥4 级［20］，这里的震级为日本气象厅（JMA）给出的震级，该震级在4～8级范围内与Ms 震级的差异可以忽略不计［28］；震源距范围25 km～200 km，保证地震记录至少有3 s P 波且尽可能包含近海地震事件；信噪比（SNR）大于10 dB，减小噪声对震级估算的影响［12，29］；三分向合成加速度的峰值大于2 Gal［30］。此外，为保证数据质量和使用，对下载的记录进行了常规处理：检查记录的基线并进行校正；采样频率统一为100 Hz；自动捡拾P 波到时并人工校验。经过数据筛选和处理后，共获得28 018 条竖向地震加速度记录，作为验证和对比的数据集，涉及3 519 次4～9 级地震事件，不同记录数量随震源距和震级的分布如图1所示。

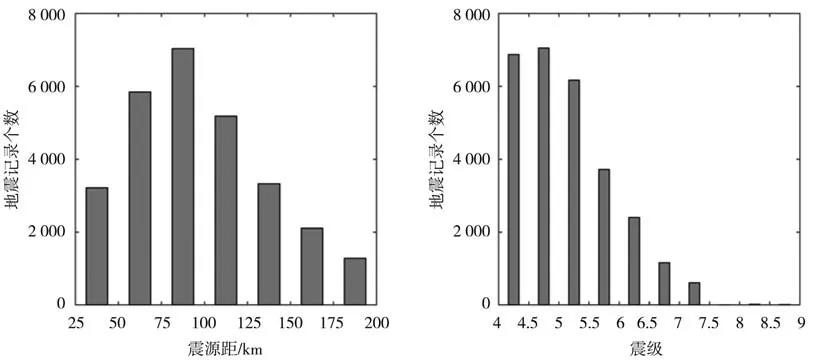
图1 地震记录数量随震源距和震级的分布Fig.1 Distribution of seismic record number with source distance and magnitude

2 累积绝对位移值估算震级方法

2.1 预警参数CAD

地表的变形在一定程度上可以反映地震的大小，预警参数Pd是P波到达后几秒内位移的最大幅值，早在Wu等［14］就通过研究发现当震源距已知时，可以通过Pd建立估算震级的经验公式。此后，多数研究也表明Pd估算震级的准确性要比其他参数好得多［17-22］，也被广泛应用于各个已建地震预警系统中［23-27］。然而，Pd参数仅能代表最大变形与震级的关系，并不能反映出变形过程（断层破裂过程）与震级的相关性，为此，本文提出累积绝对位移值CAD，CAD与Pd参数相比，既包含了Pd参数所代表的最大变形信息，也包含了变形的过程信息，具有更多的与震级相关的信息。

在利用强震记录计算CAD时，需要对加速度记录进行2次积分得到位移记录，再累积取绝对值的位移记录，CAD的计算公式如式（1）：

式中，a（t）代表t时刻加速度（Gal），T代表了初至地震波的时长（s）。在CAD的计算过程中，为避免积分计算引入长周期误差，采用与Pd参数计算过程中相同的数据处理方法［12］，即在每次积分后对记录进行0.075 Hz的高通滤波（2阶Butterworth）。

2.2 估算震级

震级的估算是通过建立CAD、震源距和震级的经验公式来实现的，经验公式的形式与Pd是相同的，如公式（2）所示：

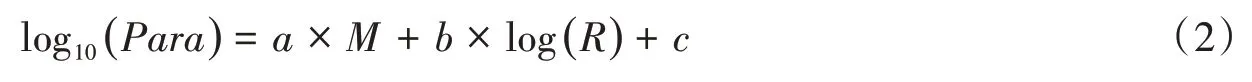
式中，Para是预警参数（CAD或Pd）；M是震级；R是震源距；a，b，c是待定的回归系数。回归系数是通过大量地震记录的回归分析得到，在利用不同时长初至地震波估算震级时，需要采用相应时长初至地震波的回归系数。

3 计算结果

3.1 初至3 s时P波的震级估算

地震预警系统属于秒级数据处理和信息发布系统，在P波震相到达后，越快速地给出具有一定准确性的震级，就可以争取到越多的预警时间。多数研究结果表明［11-12，14，31］，采用初至3 s P 波估算的震级较好地兼顾了地震预警的时效性和准确性，可以用于发布预警信息。因此，提高初至3 s P 波时估算震级的准确性尤为重要。利用前述历史地震记录数据集的初至3 s P波回归分析公式（2），分别得到CAD和Pd与震级、震源距的经验公式（3）和（4）。为便于图形展示和分析震级与CAD、Pd的相关性，利用震源距将CAD、Pd归一化到震源距10 km 处［32］，震源距归一化后，Pd用Pd10表示，CAD用CAD10表示。由图2 可以看出，取对数后的CAD10和Pd10均与震级呈现出了较好的线性关系，与震级的相关系数CAD10略高于Pd10（CAD10为0.80 和Pd10为0.76）；CAD10和Pd10与震级的线性关系在不同的震级范围内存在差异，对于约6.5级以上地震事件，CAD10和Pd10总体上随着震级的增大而减小，特别是7级以上地震尤为明显，表现出了饱和的情况，这与多数学者所发现的“震级饱和”问题是一致的［11，14，22，32］。

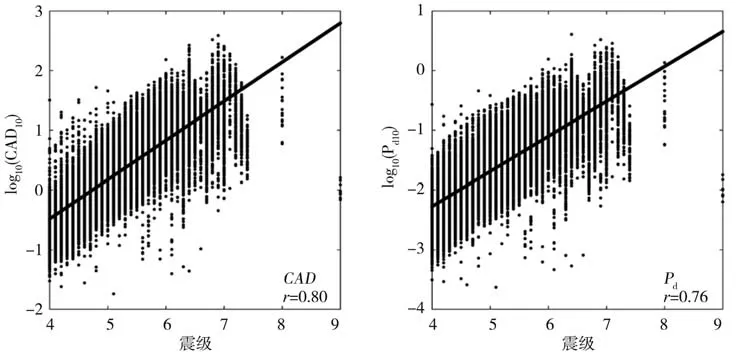
图2 CAD10、Pd10与震级的相关性Fig.2 Relationship between CAD10、Pd10 and magnitude

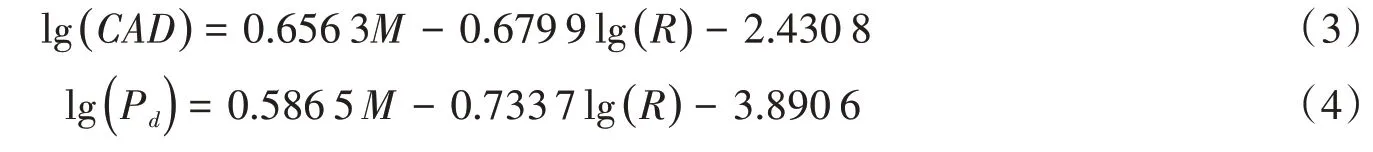
利用式（3）和式（4）估算震级，对比CAD和Pd估算震级的效果。图3 为真实震级与估算震级的误差分布：由图可以看出用CAD估算震级的误差的离散性略小，且误差标准差更小（CAD为0.58，Pd为0.66）；CAD和Pd估算震级的误差分布在不同震级范围内是不一致的，对于6.5级以上地震事件，也表现出了图2中的“震级饱和”的问题。

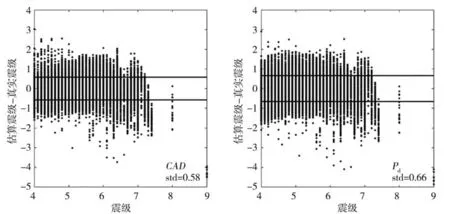
图3 估算震级的误差分布Fig.3 Estimated magnitude error distribution

为了更直观的展现CAD和Pd估算震级的误差分布情况，作震级误差分布直方图（图4）。由图明显看出CAD和Pd估算的震级误差极少数分布在±1 个震级范围外，少部分分布在（0.5，1）和（-1，-0.5）震级范围之内，大多数分布在［-0.5，0.5］震级范围内，且在［-0.5，0.5］震级范围内CAD的占比（误差在震级范围内的记录数量/总记录数量*100%）约是Pd的1.2倍（CAD为63%，Pd为55%）。

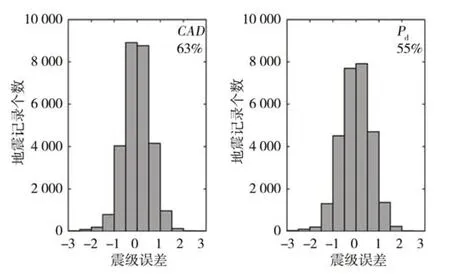
图4 震级误差分布（百分数为占比）Fig.4 Magnitude error distribution

进一步对比CAD和Pd估算震级误差随震级的变化，图5 为平均绝对误差随震级的变化情况：可明显看出，两参数的平均绝对误差均随震级的增大而增大，CAD在［4，6］级范围内估算震级的平均绝对误差明显小于Pd，在6 级以上时估算震级的平均绝对误差与Pd差别很小。值得注意的是，7.3 级以上地震CAD和Pd估算震级的平均绝对误差过大，超过了1个震级误差。

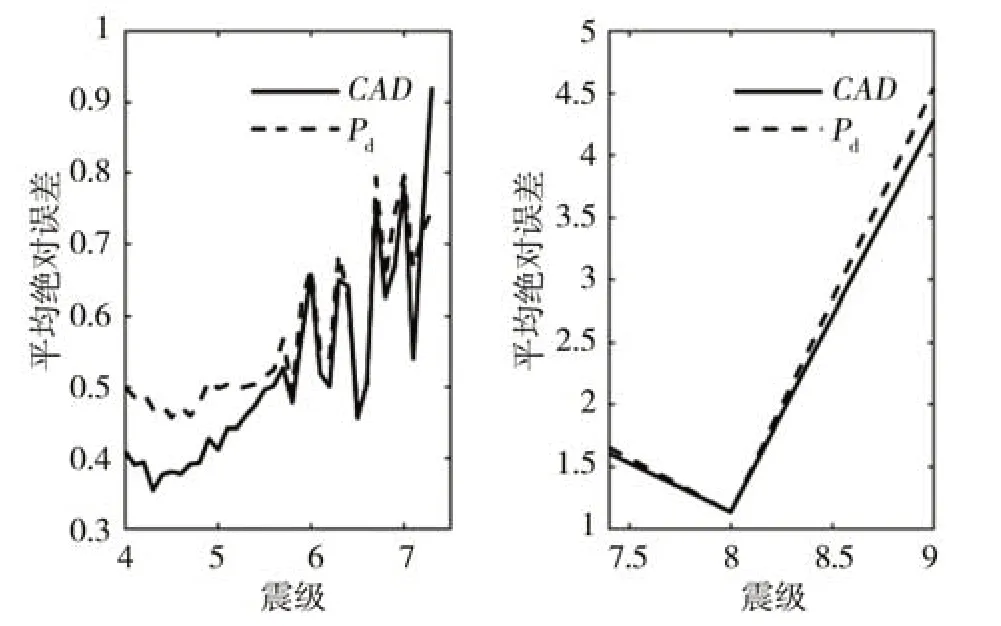
图5 平均绝对误差Fig.5 Mean absolute error

3.2 在不同时长初至地震波时的震级持续估算

考虑到地震预警中的震级估算是随着初至地震波时长的增加而不断更新的过程，一般来说地震波时长越长越有利于震级估算的准确性。在前述结果的基础上，进一步持续增加初至地震波时长检验CAD方法和Pd方法的持续震级估算效果。利用P波到达后的4 s、5 s和6 s 地震波求得参数CAD和Pd，通过最小二乘回归分析式（2），分别得到CAD和Pd与震级的经验公式并估算震级，其回归系数如表1所示。

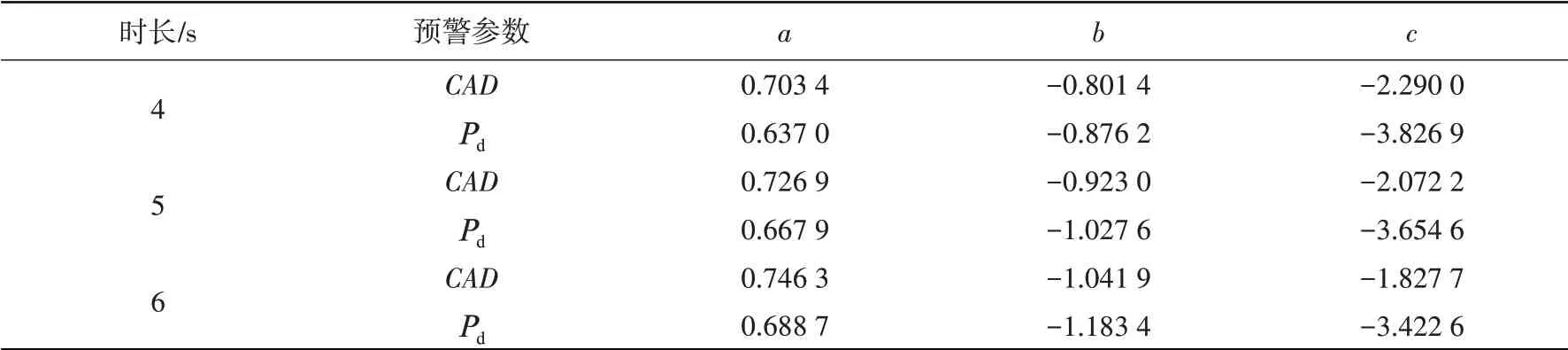
表1 经验公式的回归系数Table 1 Regression coefficients of empirical formulas

为了分析参数CAD和Pd与震级的相关程度和估算震级误差的离散程度，作相关系数图和误差标准差图进行对比（图6）。图6（a）表示震源距归一化后的CAD和Pd分别与震级的相关系数随时间的变化趋势：从图中可以看出，两参数的相关系数均随地震波时长的增加而有所提高，而CAD10与震级的相关系数整体上明显高于Pd10，且CAD10在3 s、4 s、5 s和6 s时与震级的相关系数都达到0.8以上，呈高度相关。图6（b）表示CAD和Pd估算震级的误差标准差随时间的变化情况：由图可看出，两者估算震级的误差标准差均随地震波时长的增加而降低，CAD的误差标准差明显小于Pd；总体来看，CAD10与震级的相关系数始终大于Pd10，CAD估算震级的误差标准差始终小于Pd。

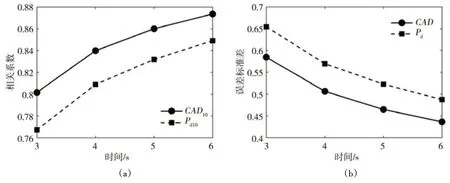
图6 相关系数和误差标准差Fig.6 Correlation coefficient and error standard deviation

进一步讨论CAD和Pd估算震级的误差分布情况。图7给出了P波到达4 s、5 s和6 s时，CAD和Pd估算震级误差的条形分布情况：由图可以明显看出，不同时长下，CAD和Pd估算的震级误差少部分分布在（0.5，1）和（-1，-0.5）震级范围之间，大多数分布在［-0.5，0.5］震级范围内；在［-0.5，0.5］震级范围内，CAD和Pd的占比随着地震波时长的增加而增加，CAD的占比始终是Pd的1.1倍。

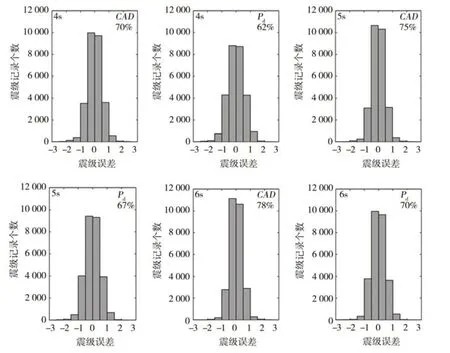
图7 初至4 s～6 s地震波估算震级的误差分布（百分数为占比）Fig.7 Error distribution of estimated magnitude using initial 4 s～6 s wave

进一步分析不同震级下持续估算震级的准确性。图8代表P波初至4 s，5 s和6 s时，CAD和Pd估算震级的平均绝对误差随震级的变化情况，由于大震饱和使7.3级以上的估算出现明显的震级低估，平均绝对误差相比其他震级来说过大，不进行分析对比，故只选取7.3 级以下的地震数据研究。由图8 可看出：在同一时刻，CAD与Pd的平均绝对误差都随震级的增大而增加；不同时刻间，二者的平均绝对误差都随地震波时长增加而减小；初至地震波时长4 s 时，CAD在［4-6］级范围内估算震级的平均绝对误差要明显比Pd更小，6 级以上两者的平均绝对误差相差不大；初至地震波时长5 s 和6 s 时，CAD在［4-6.3］级范围内估算震级的平均绝对误差要明显比Pd更小，6.3级以上两者的平均绝对误差相差不大。

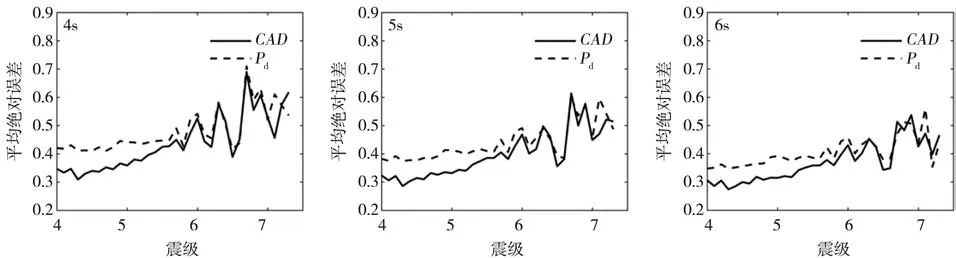
图8 初至4 s ～6 s地震波估算震级的平均绝对误差Fig.8 Mean absolute error of estimated magnitude using initial 4 s～6 s wave

4 震例测试

以2019 年6 月18 日日本新潟发生的6.7 级地震为实例，评估CAD的震级估算效果。该地震为日本近海海域典型地震，震级为6.7级，震中位置（38.6°N，139.5°E），震源深度为14 km。地震造成了房屋破坏、列车停车、公路塌陷、滑坡、液化等问题。地震发生时，日本JMA 向公众发布了地震预警信息［33］。图9 为最先触发4 个KiK-net 地表监测台站的CAD和Pd持续估算震级的结果（首个监测台站YMTH13 的P 波到时记为横轴0 s），每个台站都在P波到达后3 s，开始以1 s间隔持续估算震级，当初至地震波时长为6 s时停止估算震级。由图9 可以明显看出，随着地震时间的增长，CAD和Pd估算的震级整体呈上升趋势；4 个台站中CAD估算震级的最大偏差为+0.7个单位震级，Pd估算震级的最大偏差为+1.0个单位震级，且CAD估算震级的离散性比Pd更小。

图9 持续估算震级Fig.9 Continuous magnitude estimation

进一步利用JMA 公布的地震预警信息对比分析震级估算效果。鉴于JMA 在首个监测台站P 波到时后的5.2 s，7.3 s，8.0 s，9.0 s 和9.9 s 持续更新了地震预警信息，取CAD和Pd在首个监测台站P 波到达后5.0 s-10.0 s时，各台站估算震级的平均值作为最终估算震级进行对比。对比结果如图10所示（首个监测台站的P波到时记为横轴0 s）。从图10中可以看出，在5 s，7 s和8 s时（6 s时，JMA 未给出预警信息），CAD估算的震级与真实震级最为接近，其次是Pd方法，JMA 估算的震级偏小了约0.6 个震级；在9 s 和10 s 时，JMA 估算震级偏高了约0.2 个震级，CAD偏高了0.4 个震级，Pd偏高了0.5 个震级。需要注意的是，CAD和Pd仅利用了KiK-net的4 个地表台站的数据估算震级，而JMA 利用更多监测台站（如KiK-net井下台站、K-net台站、Hi-net台站等）的数据估算震级。总的来看，CAD在本次地震中估算震级的偏差是小于JMA和Pd的估算结果的。

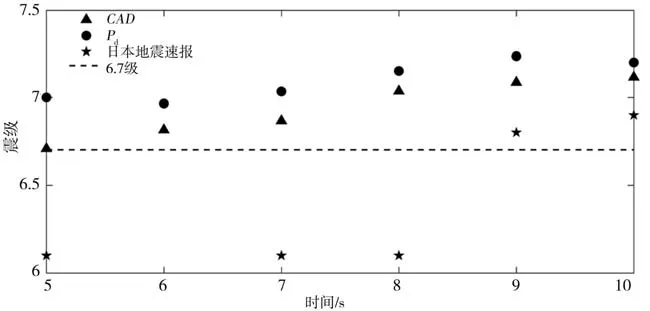
图10 持续估算震级平均值Fig.10 The average of estimated magnitude

5 结论

（1）为提高地震预警中震级估算的准确性，提出了一种新的震级估算方法，即利用初至地震波的CAD建立震级的经验公式。CAD的计算过程是，通过对加速度记录进行两次积分得到位移记录，再对位移记录取绝对值后求累积。在这个过程中，CAD利用了初至地震波引起的地表变形的所有信息，间接地包含了断层的初始破裂过程信息。相比于广泛使用的Pd参数（仅利用地表最大变形信息），CAD在理论上可以保留更多与震级估算相关的信息。

（2）利用日本KiK-Net 数据库中28018 条地表强震观测记录（震级范围4～9 级）对CAD估算震级效果进行了验证，并与当前普遍采用的Pd方法进行了对比。结果表明，对于4～7.3 级地震，初至地震波时长为3 s～6 s 时，CAD估算震级的效果随着地震波时长的增加不断改善，并且与震级的相关性比Pd大，估算震级的误差标准差比Pd小，估算震级误差在［-0.5，0.5］震级范围内的占比是Pd的1.1～1.2倍。这证明了，利用变形过程信息的CAD比仅利用最大变形信息的Pd更有利于震级的估算，CAD可以为地震预警系统提供更准确的震级估算。

（3）在日本近海6.7 级典型地震事件的测试中，CAD估算震级的偏差总体上是小于JMA 和Pd的估算结果，这表明CAD用于实际地震预警系统具有可行性。

致谢：

感谢日本防灾科学技术研究所（NIED，https：//www.doi.org/10.17598/NIED.0004）提供了KiK-net 强震数据下载服务。