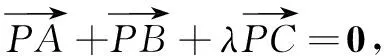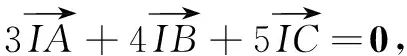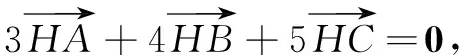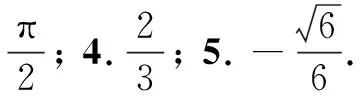一道向量试题的解法探究及拓展应用

毛晓伟 王 义

(安徽省砀山中学，235300)

笔者所在学校在2022届高三模考中,试卷命制了一道以向量为背景的三角形外心问题,学生的解答不尽人意,得分率很低.在讲解过程中,师生从不同角度进行探究,通过观察、思考,让学生挖掘与三角形“四心”有关的性质与结论,并进行简单应用,培养了学生发现问题、分析问题和解决问题的思维能力,提升了学生的数学学科核心素养.现整理成文与同行分享,不足之处,敬请指正.

一、试题呈现

二、解法探究

解法1基底表示法

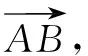
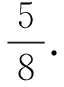
解法2向量表示法

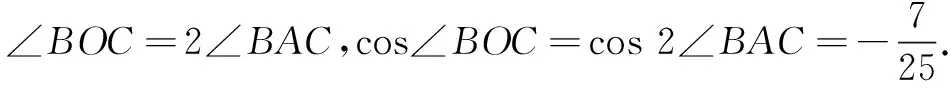
解法3几何法

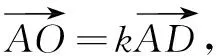
解法4坐标法

解法5利用外心的性质

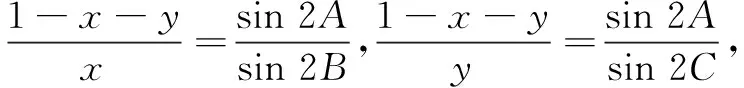
三、探究拓展

近年来,各类考试对三角形四心的考查屡见不鲜.当点O分别为三角形的外心,内心,重心,垂心时,又有什么优美的结论呢?

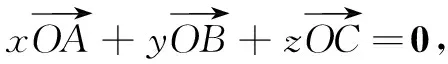
S∆BOC∶S∆AOC∶S∆AOB=|x|∶|y|∶|z|.

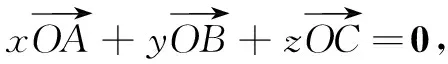
同理有S∆AOC∶S∆ABC=|y|∶|x+y+z|,S∆AOB∶S∆ABC=|z|∶|x+y+z|.所以S∆BOC∶S∆AOC∶S∆AOB=|x|∶|y|∶|z|.

结论1在∆ABC中,角A,B,C所对的边分别为a,b,c,若O为∆ABC的外心,则有

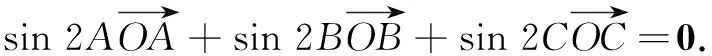
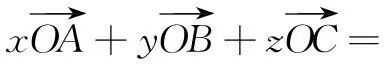
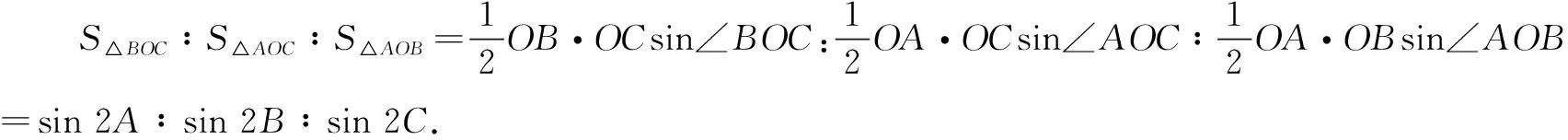
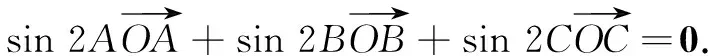
结论2在∆ABC中,角A,B,C所对的边分别为a,b,c,若O为∆ABC的内心,则有

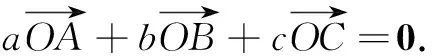
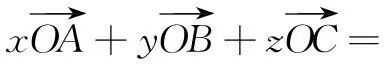
结论3在∆ABC中,角A,B,C所对的边分别为a,b,c,若O为∆ABC的重心,则有

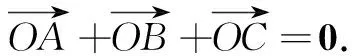
由重心的性质易证明结论3,此处从略.

结论4在∆ABC中,角A,B,C所对的边分别为a,b,c,若O为∆ABC的垂心,则有

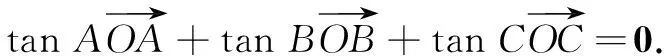
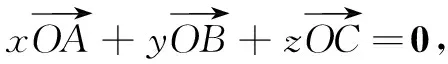
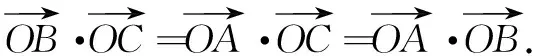
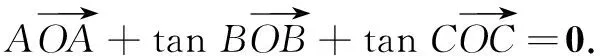
四、应用举例

利用上述优美结论,不难解决如下问题(限于篇幅,解答过程从略,读者不妨试一试).