适用于MMC-HVDC的定频模型预测控制策略
2022-04-08聂小鹏郭汉臣
聂小鹏, 王 琛,2, 王 毅,2, 郭汉臣
(1.新能源电力系统国家重点实验室(华北电力大学),河北 保定 071003;2.河北省分布式储能与微网重点实验室(华北电力大学),河北 保定 071003)
0 引 言
凭借拓展性好、运行损耗低及波形质量高等优势,基于模块化多电平换流器(Modular Multilevel Converter,MMC)的高压直流输电(High Voltage Direct Current,HVDC)系统成为研究热点,且已获得了实际工程应用[1-4]。柔性直流输电系统的站级控制多采用经典的双闭环矢量控制方法,该方法在同步旋转坐标系下建立换流器的数学模型,有功、无功解耦控制特性良好。然而,当MMC-HVDC采用双闭环矢量控制方法时,由于子模块电容电压、相间环流等控制参量较多[5-11],比例-积分(PI)环节与前馈解耦环节会产生较长的控制延迟,使得该方法的应用具有一定的局限性[12]。
针对传统MPC存在的问题,已有多种适用于MMC-HVDC的改进MPC策略被相继提出。文献[16-18]采用分层控制,将传统MPC中统一的指标函数进行分解,根据不同控制目标分别建立指标函数,避免了权重因子的整定。文献[19]将冒泡排序算法引入MPC,改善了子模块的均压效果并减少了系统计算量,但排序变化引发了额外的开关动作,会增大器件开关频率。通过在电压排序算法中引入误差因子,文献[20]大幅降低了传统MPC的计算量,并进一步减小了子模块电压的波动范围。文献[21]提出了一种简化MPC策略,通过构建有限控制集对电容电压修正后再进行排序,有效减少了循环计算和预测值计算次数。文献[22]提出了一种堆排序和归并排序相结合的排序算法,在维持电容电压平衡的同时减少了系统可能的开关状态,但排序过程中仍存在器件开关频率较高的问题。已有MMC-HVDC的改进MPC策略大多无需整定权重因子且可降低系统计算量,但器件开关频率较高的问题仍未得到有效解决。为此,本文提出了一种基于固定频率的模型预测控制(Fixed Frequency MPC,FF-MPC)策略,该策略由独立的指标函数控制各系统目标以及频率固定控制两部分组成。通过独立的指标函数进行分层控制,使模型预测控制所要计算的开关状态组合数大幅减少,利用排序均压算法中引入的保持因数与开关频率之间的反比例关系构建反馈控制,对电容电压排序进行调整,从而实现开关频率的固定控制,进一步解决开关器件开关频率高的问题。
本文首先介绍了MMC等效电路,并在此基础上推导得出MMC各个控制目标下一时刻的预测值。其次,提出基于固定频率的模型预测控制(FF-MPC),分别建立对应于交流电流追踪、相间环流抑制以及子模块电容电压均衡控制的指标函数,并搭建了频率固定控制器。最后,在Matlab/Simulink仿真模型中对FF-MPC控制策略的有效性与优越性进行了验证。
1 MMC数学模型
三相MMC每相包含上、下两个桥臂,每个桥臂由N个子模块和一个桥臂电感串联构成。通过控制功率器件IGBT的通断,级联的N个子模块能够输出多种电平,因此可等效为一个输出电压为阶梯波的受控电压源,进而得到MMC的等效电路,如图1所示。
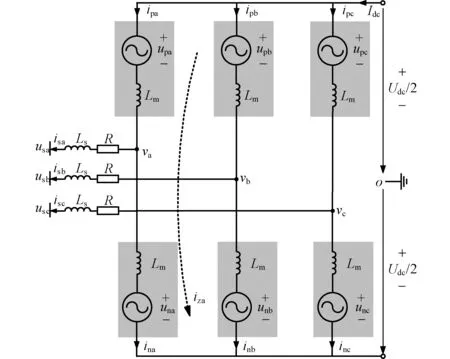
图1 MMC等效电路Fig. 1 Equivalent circuit of the MMC
图1中,usj、isj(j=a、b、c)表示交流电网侧电压与电流;ipj、inj(j=a、b、c)分别表示j相上下桥臂电流,其参考正方向如图中标注所示;upj、unj(j=a、b、c)分别表示j相上桥臂与下桥臂输出电压;Udc、Idc表示直流母线的电压和电流。izj(j=a、b、c)为相间环流;Ls、Lm和R分别为交流侧电感、桥臂电感和交流侧电阻。
对桥臂电流进行分析,由于MMC的桥臂对称,可以认为系统输出电流isa、isb、isc在MMC各相上下桥臂均分,即交流系统为各相上下桥臂分别提供电流isj/2(j=a、b、c)。直流电流Idc在三相均匀分配,即直流侧为三相分别提供电流Idc/3。综合考虑交流侧和直流侧与环流的影响,由叠加定理得:
(1)
对式(1)进行相加得到环流的表达式:
(2)
对上下桥臂运用KVL定理,根据图1所示电流方向可得:
(3)
考虑桥臂中点的节点KCL方程可得相电流表达式:
isj=ipj-inj
(4)
结合式(2)、式(3)和式(4)可得MMC交流侧与直流侧电压数学模型:
(5)
(6)
式中:vj表示MMC交流侧j相输出电压。
由式(5)可以看出,上、下桥臂等效电压的差值与决定了交流侧电流的大小。同理由式(6)可以看出,上下桥臂等效电压之和与直流侧电压之间的不均衡直接影响环流的大小,因此,控制子模块投入个数即可对环流进行控制。
2 基于固定频率的模型预测控制
针对于传统MPC控制中循环计算开关状态组合数庞大以及开关频率高的问题,本文提出一种基于固定频率的模型预测控制,该方法通过独立指标函数依次进行交流侧电流追踪、环流抑制以及子模块均压,减少需要循环的开关状态组合数,并将频率固定控制与子模块电容电压均衡控制相结合,实现对频率的固定控制。
2.1 追踪交流电流控制
追踪交流侧电流即使MMC交流侧电流精确跟踪三相参考电流,从而减少谐波,提高电能质量。设一个采样周期为Ts,得到交流电流随时间的导数为
(7)
将式(7)带入式(5)得到MMC交流电网侧电流预测值:
(8)
式中:K=R+Leq/Ts;Leq=Ls+Lm/2;usj、isj(t+Ts)为下一时刻交流电压与电流的预测值;isj(t)为交流电流实际值;upj(t+Ts)、unj(t+Ts)为下一时刻上下桥臂等效电压的预测值。
为了使系统能够精准的跟踪三相参考电流,采用下一时刻交流电流预测值与参考值构建指标函数G1:
G1=|isj_ref(t+Ts)-isj(t+Ts)|
(9)
从式(8)中可以看出交流侧电流与MMC输出相电压vj有直接关系,对于上下桥臂各有N个子模块的MMC来说,根据MMC输出特性,可得上下桥臂等效输出电压upj、unj取值范围{0,Udc/N,…,(N-1)Udc/N,Udc},输出相电压vj的取值范围:
(10)
交流电流控制流程如图2所示,上、下桥臂投入子模块数量分别为Sp与Sn。从式(10)可知输出相电压一共有N+1种状态组合方式,即为了实现系统的追踪交流侧电流控制,首先将所有状态组合下的上、下桥臂输出电压值和系统交流侧电压、电流采样值代入公式(8)求得交流电流预测值,其次将得到的交流电流预测值和参考值代入指标函数G1进行评估,选出G1差值最小时所对应的桥臂投入数目imin,imin即为上桥臂应投入的子模块数目,N-imin则为下桥臂应投入的子模块数目。
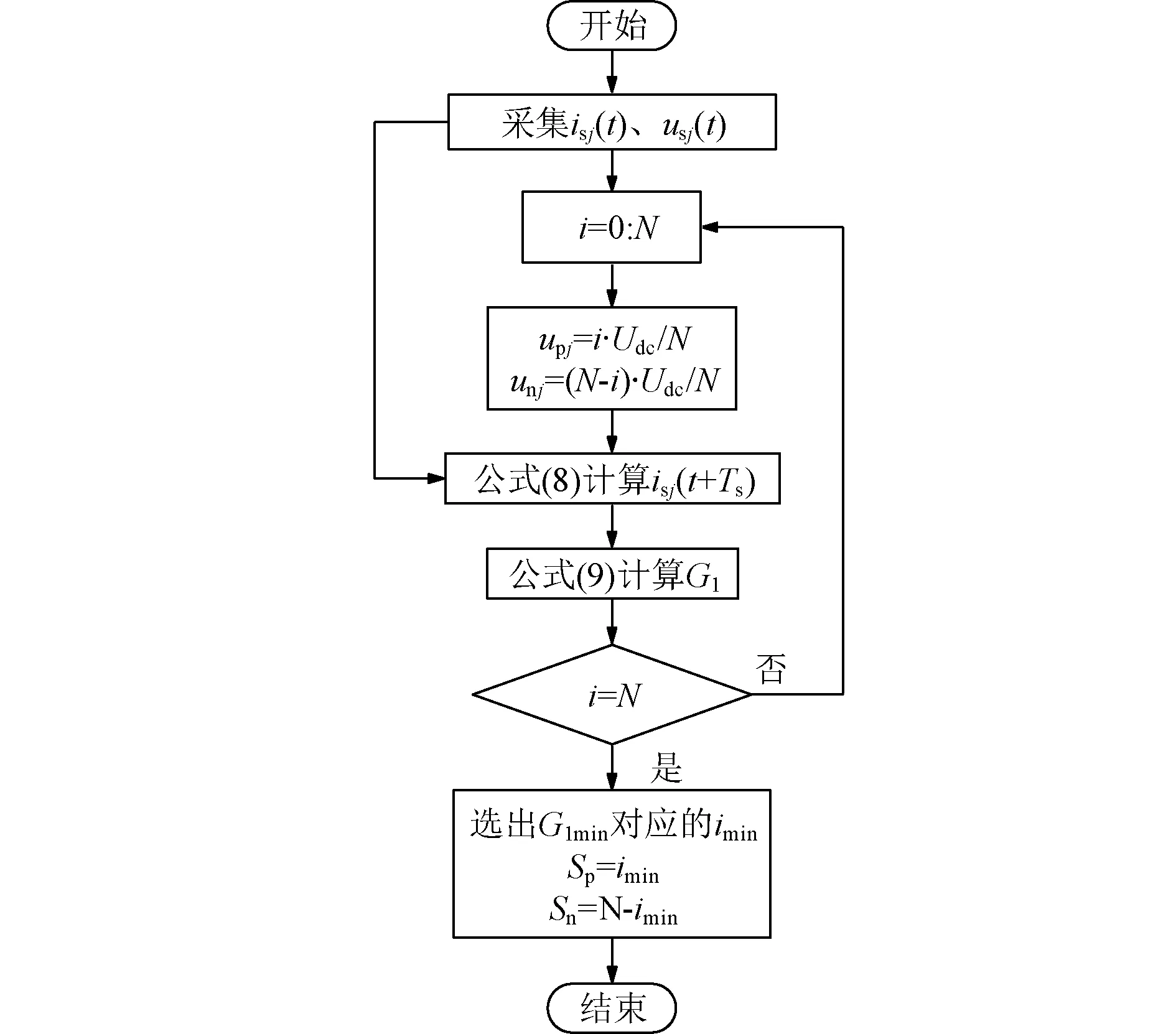
图2 交流电流控制流程图Fig. 2 Flow chart of control AC current
2.2 环流抑制控制
环流产生的本质是上、下桥臂投入子模块电压之和与直流侧电压存在偏差,抑制环流的目的就是尽可能减小两者的偏差。将环流的有效抑制最后落实到子模块的投切上,可视作在上下桥臂同时增加投入一个子模块或减少投入一个子模块来减小这个偏差,从而实现动态抑制。本文采用单模块补偿策略,即上下桥臂子模块数改变量为1个,补偿电平Uadd的取值范围为{-Udc/N,0,Udc/N}。
根据式(6)可得相间环流预测值为
(upj(t+Ts)+Uadd)]+izj(t)
(11)
为了抑制相间环流,建立指标函数G2:
G2=|izj_ref(t+Ts)-izj(t+Ts)|
(12)
环流抑制控制目的是得到最终的上下桥臂子模块投入数目,其控制流程图如图3所示,其中Spon和Snon为环流抑制修正后上下桥臂的投入数目。具体实现过程是,首先计算3次不同补偿电压状态,得出上下桥臂电压的修正量,将其代入公式(11)得到环流的预测值,其次将预测值代入指标函数G2进行评估,选出可使环流达到最小的修正量,即可达到环流抑制的目的,至此得到最终的桥臂投入子模块数目。
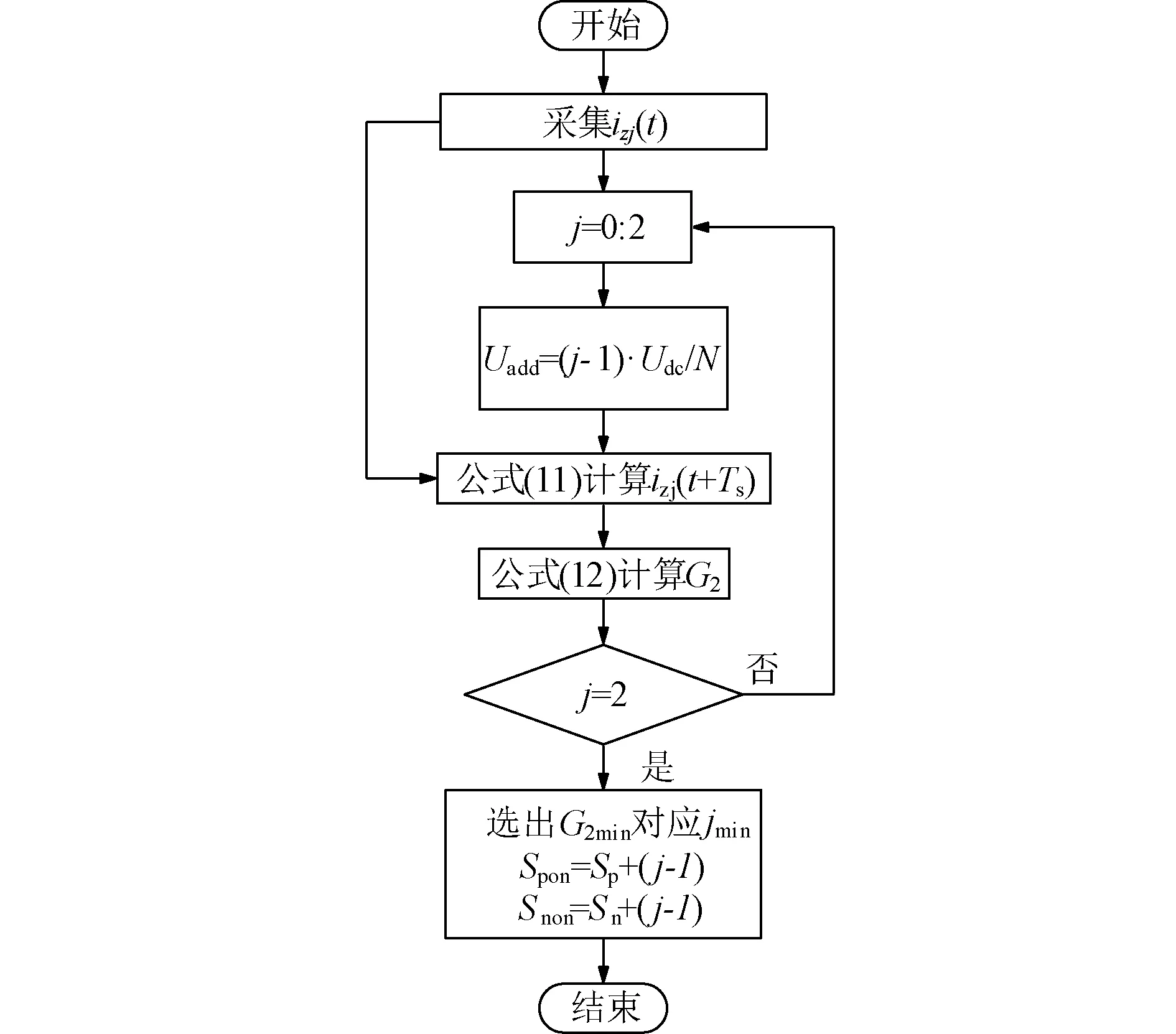
图3 环流抑制流程图Fig. 3 Flow chart of circulation suppression
2.3 电容电压均衡与固定开关频率融合控制
子模块电容电压预测值由当前时刻子模块的投切状态决定,若当前时刻判定子模块为关断状态,则下一时刻子模块电容电压不发生改变,若当前时刻子模块开通,则预测值为
(13)
式中:ucj(j=1,2,…,N)为子模块电容电压;imj(m=n、p)为上下桥臂电流。
建立电容电压均衡的指标函数G3:
(14)
根据指标函数G3计算当前时刻所有子模块电容电压与参考电容电压的误差值,选择误差最小的子模块,直到选取的子模块个数达到环流抑制控制求得的上下桥臂投入子模块个数,将其确定为下一周期MMC需要导通的子模块,即每相开关状态需计算的次数为2N次,就能确定下一时刻MMC投入的子模块。
为了降低开关频率,本文在排序均压环节中引入保持因数,通过保持因数使各子模块在下个时刻的触发脉冲中尽可能保持当前的工作状态,从而减少排序次数,降低开关频率。基于保持因数排序法的原理如下:倘若桥臂电流方向为正,子模块为充电状态。对于已投入的子模块且电容电压值超过下限umin的,将子模块的电容电压乘以1/HF(HF>1)来继续减小电容电压值,以此增加该子模块在当前时刻继续保持投入状态的概率;倘如电流方向是负,子模块为放电状态。对于已投入的子模块且电容电压值超过上限umax的,子模块的电容电压乘以HF来增大电容电压值,以此来增加被投入的概率。倘若该子模块上一个时刻是切出状态,则该子模块的电容电压维持实际值不做处理。
经过上述分析引入保持因数后的电容电压均衡指标函数修正为
对于换流器来说,开关频率高会导致系统损耗大,开关频率不固定导致系统稳态跟踪性能差、电感参数的计算选取困难。本文提出了一种优化的定频控制方法,通过保持因子系数对参与排序的电容电压进行处理,增大上一个时刻投入子模块在当前时刻投入的概率,以此来降低开关频率并实现定频控制。
在实现定频控制之前,首先需要解决的是平均开关频率的计算问题。对于并网换流器来说,系统电压和电流的频率为50 Hz,桥臂的调制电压同为50 Hz,因此在一个工频周期内,同一桥臂的所有开关器件的平均开通次数也呈现出周期性特性,同一桥臂的平均开关频率可采用平均开通次数除以时间周期来计算。本文选择文献[23]中的移动平均值计算方法来计算桥臂的平均开关频率,平均开关频率计算的周期是0.02 s。计算公式如下:
(16)
式中:Ton(t)表示的是某一个桥臂在当前时刻的平均开关次数,其具体计算公式如下所示:
(17)
式中:Ti表示当前时刻某一个桥臂中某一个子模块的开关次数,i=1~N。其具体的计算方法为,根据上一个时刻的开关状态和当前时刻的开关状态判断子模块当前时刻的开关次数为0还是为1,只计算开通的次数,例如上一个时刻为关断,当前时刻为开通,则开关次数是1,其余情况开关次数为0。
频率固定控制原理框图如图4所示,由开关频率测量单元、频率固定单元以及电容电压均衡单元组成。首先通过开关频率测量单元得到桥臂平均开关频率Fs后进入频率固定单元,从上文中基于保持因数排序法的原理我们可以得知,随着保持因数的增大,开关频率会进一步降低,利用保持因数和开关频率之间的反比例关系,搭建频率固定器,将频率给定值Fref和频率实际值Fs的差值经过PI调节器处理后得到子模块的电容电压保持因数HF,再将保持因数送入电容电压均衡单元改变排序顺序,从而减少排序次数,降低开关频率,使实际开关频率Fs不断逼近开关频率给定值,从而完成定频控制。
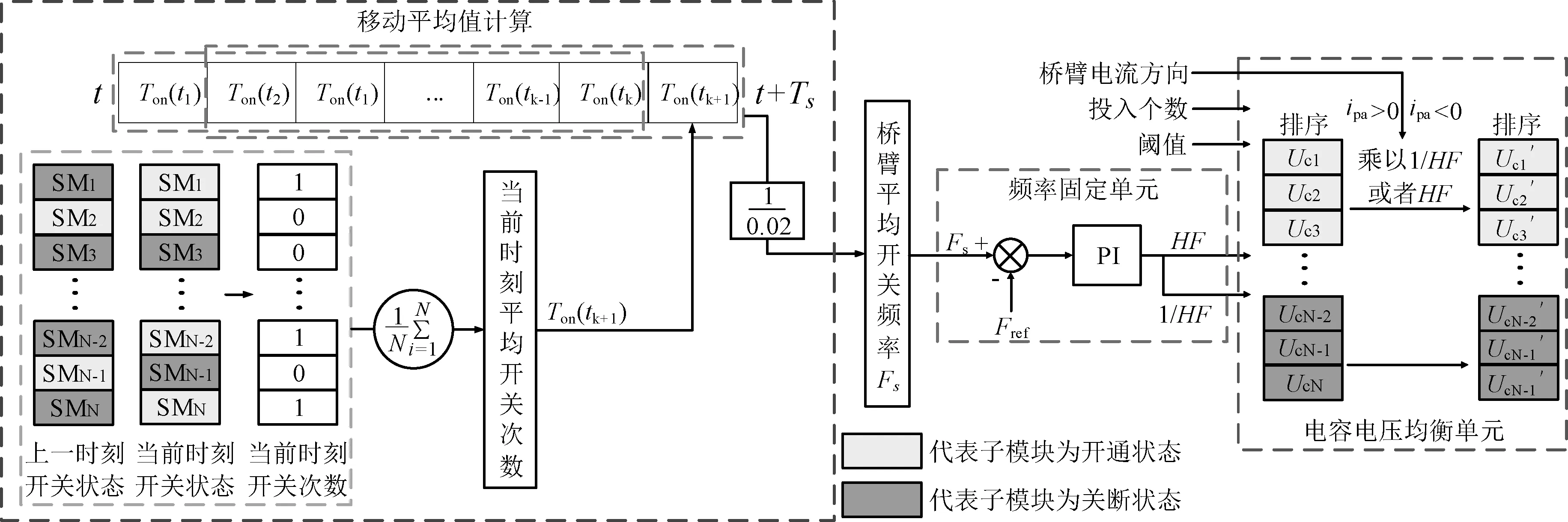
图4 定频控制原理图Fig. 4 Fixed frequency control principle diagram
3 仿真验证
为了验证本文所提出的基于固定频率的模型预测控制的有效性,在Matlab/Simulink中分别搭建了FF-MPC控制以及传统MPC控制下的11电平MMC模型。仿真主要参数如表1所示,其中传统MPC的交流电流控制权重因子为1.0,环流控制的权重因子为3,电容电压均衡控制的权重因子为0.6。
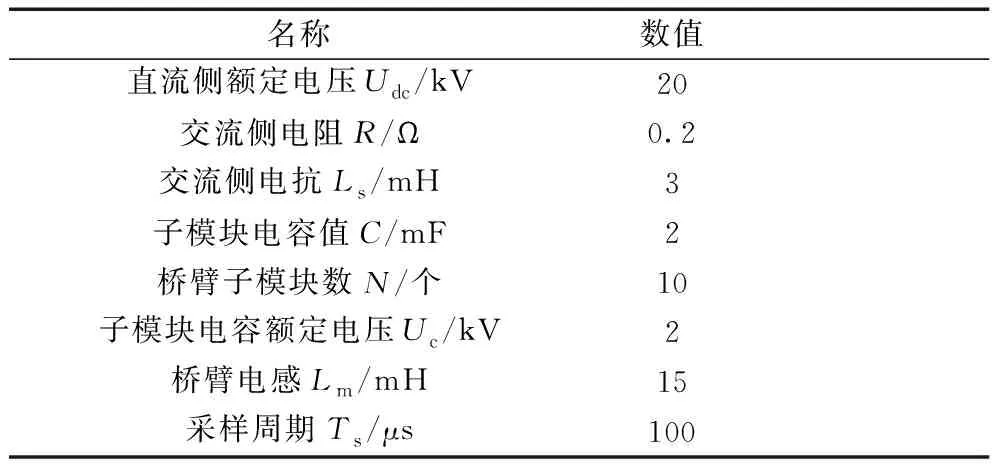
表1 仿真参数Tab.1 Parameters of simulation model
为了验证本文所采用的定频控制的有效性,FF-MPC控制以及传统MPC控制下的开关频率与子模块开关频态如图5所示。图5(a)为传统模型预测控制的开关频率,开关频率为380 Hz。图5(b)为双阶跃下FF-MPC开关频率波形图,在2 s和3 s时频率固定值分别阶跃至200 Hz与100 Hz。0-2 s未投入定频控制时,MMC开关频率为300 Hz,可以看见在定频控制启用之前,开关频率相较于传统模型预测控制已大幅减少,验证了本文采用独立指标函数控制系统目标,降低了换流器各相的开关状态组合数能从而有效降低开关频率。在2 s与3 s时刻进行定频控制,频率参考值发生阶跃变化,MMC开关频率能够快速的跟随参考值,且定频控制响应快速,定频控制效果良好。同时,从两者控制下单个子模块的开关频态波形来看,本文所提控制能够降低子模块的开断频率,有效解决传统MPC控制开关频率高的问题。
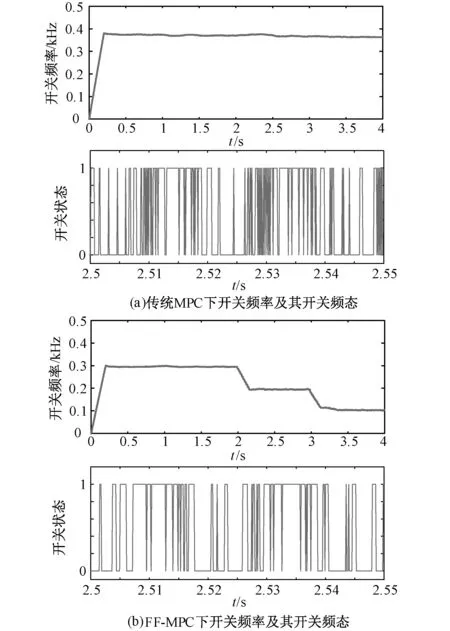
图5 定频控制仿真结果Fig. 5 Fixed frequency control simulation results
综上所述,在改进后的MPC控制下,相较于传统MPC控制子模块开关频率已大幅降低,且在定频控制下能使开关频率能得到进一步降低,实现频率的精准控制。
图6为本文所提的FF-MPC控制以及传统模型预测控制的输出波形对比图,其中FF-MPC控制在上述定频控制的工况下进行仿真。从上至下分别为MMC输出相电压、相电流、电流谐波频谱、环流波形以及子模块电容电压波形。
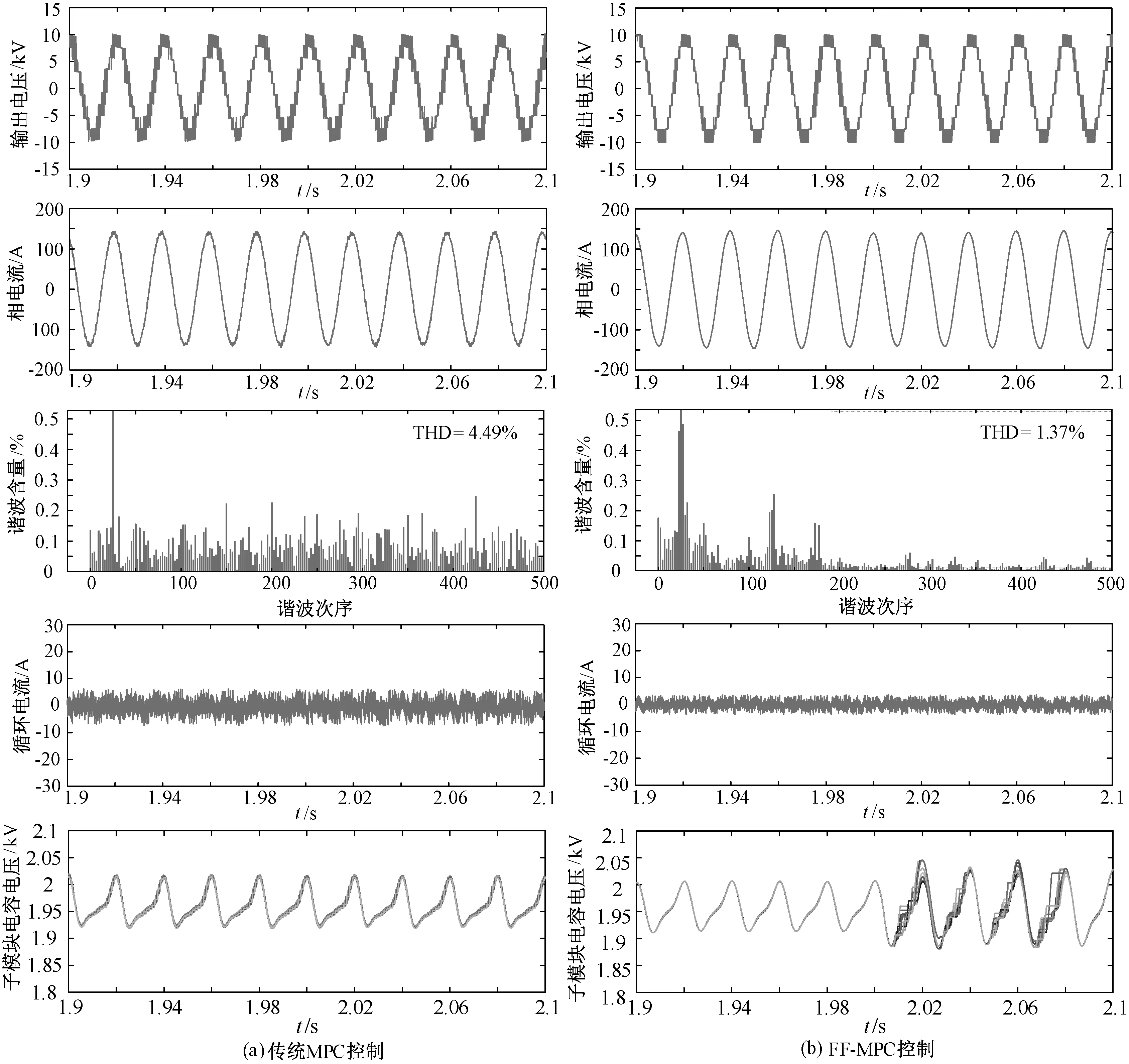
图6 两种控制下仿真结果图Fig. 6 Simulation result under two kinds of control
对比电压波形可知,MMC投入的子模块数决定了输出电压波形,传统MPC与FF-MPC下输出电压波形上的电压电平跳变则说明了模型预测控制下子模块投入个数在不断变化。在一个电平持续时间内的每一个控制周期,模型预测控制通过求解交流侧电流实际值与预测值的最优差值去选择子模块投入个数,并通过环流抑制再次修正投入子模块个数,使得电压产生多次跳变。由于差值的不固定导致其输出电压波形的电平跳跃次数不一致,因此输出电压波形中电压跳变分布较为散乱。
对比电流波形与频谱可知,相比于传统MPC下由权重因子来控制交流电流,FF-MPC控制下通过求解独立指标函数,寻找交流侧电流预测值与参考值的最优差值进而得到输出电压,使交流侧电流有着更好的追踪精度,能明显看到FF-MPC下输出电流正弦度高,无明显电流畸变。从谐波分析中得到传统MPC控制下总谐波为4.49%,而FF-MPC控制下总谐波含量为1.37%,以奇次谐波为主,低次谐波含量较高,但相对于前者高次谐波有显著减少,进一步验证了改进后的FF-MPC控制使得交流侧电流正弦度更高,谐波含量低,输出的电能质量相较于传统控制策略更好。
对比环流以及子模块电容电压波形可知,两种控制均能实现环流抑制与子模块电容电压均衡。在FF-MPC下采用补偿电平策略抑制后环流值稳定在0附近,相间环流抑制效果优于传统MPC,良好的环流抑制能够降低桥臂电流幅值,较少系统损耗。在传统MPC控制下子模块电容电压波动在±4.5%以内,在FF-MPC控制下,由于2 s后进入的定频控制需要在冒泡排序法中引入保持因数,且保持因数随着定频控制在不断变化,导致电容电压波动增大,但桥臂的10个子模块电容电压波形基本重合,电容电压值稳定2 000 V的额定值上下。电容电压波动变大,主要对器件的耐压裕度产生影响,使耐压裕度减小,但电容电压波动对于输出电压质量、输出电流、环流大小的影响很小。
图7为FF-MPC控制下A相投入的子模块数变化情况。可以看到在交流电流追踪控制下,子模块投入数为10个,在环流抑制下,投入总数围绕 10加减2来抑制环流,体现了FF-MPC下MMC投入子模块的动态变化。

图7 FF-MPC下投入子模块数Fig. 7 Number of input sub-modules under FF-MPC
图8为FF-MPC控制下MMC传输的有功和无功功率动态响应波形,在3 s时给系统一个有功功率的阶跃,此时MMC有功功率从3 MW跃变至2 MW,线路传输的有功功率迅速跟踪给定值变化,与此同时,无功功率均未发生大幅变化,稳定在0附近,这说明本文使用的模型预测控制能够根据实际需求,方便独立调节传输的有功功率,实现各物理量之间的控制,具有良好动态性能。
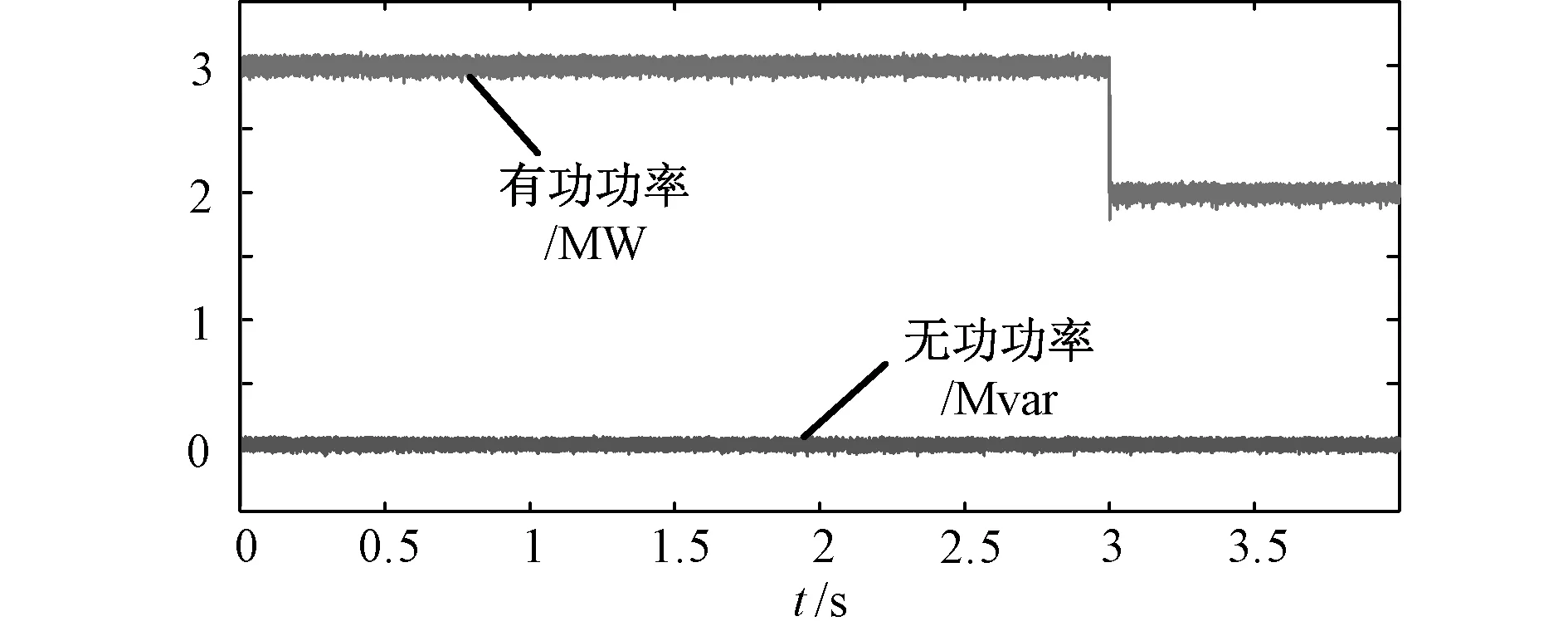
图8 有功和无功功率波形Fig. 8 Waveform of active and reactive power
从FF-MPC下的输出波形可以看出,在实现定频控制的过程中,交流侧输出电压电流,子模块电容电压,有功与无功功率传输都能稳定控制,验证了该控制方法的有效性且不与模型预测控制冲突。
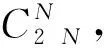
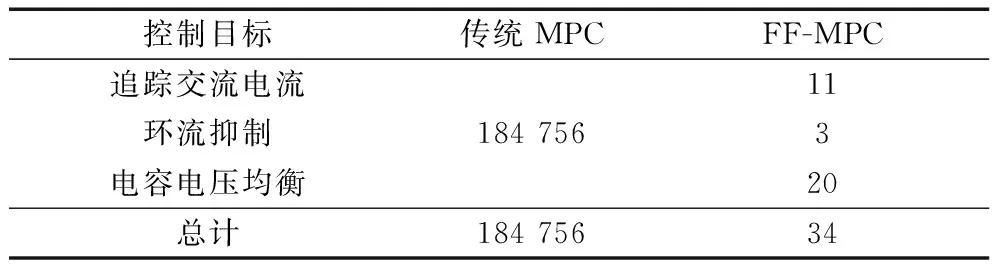
表2 两种控制方法下开关状态组合量
4 结 论
针对传统MPC控制中存在计算量庞大与开关频率高的问题,本文提出了一种基于固定频率的模型预测控制策略,并搭建仿真模型对其进行对比验证,得出如下结论:
(1)FF-MPC利用三个独立的指标函数分别求解最优值来控制交流电流、环流以及子模块电容电压,避免权重因子的整定,同时能够改善传统模型预测控制中开关状态数庞大的问题。
(2)频率固定控制效果良好,能够使子模块开关频率准确跟随参考值,完成对频率的精准控制且定频控制不影响其他系统目标控制。
(3)仿真结果表示FF-MPC下MMC输出交流侧电流质量高,谐波含量低,环流抑制效果更好,验证了本文方法的有效性与优越性。
