MMC-HVDC向无源网络供电的机电暂态等效建模研究

安文宇， 黄天啸， 任建文， 刘丽丽

(1.华北电力大学 电气与电子工程学院，河北 保定 071003；2.华北电力科学研究院有限责任公司， 北京 100045)

0 引 言

基于模块化多电平型换流器直流输电是目前柔性直流输电工程实践的主要形式[1，2]。针对含大量电力电子开关器件的柔性直流输电系统，电磁暂态仿真虽具有很好的准确性，但其求解的规模和速度受到限制[3，4]。机电暂态仿真同电磁暂态仿真相比，对于同规模电网的仿真所需计算资源较少，在可以预见的一段时间内，机电暂态仿真仍是大电网安全分析的主要手段[5，6]。

柔性直流输电的一个突出优势是可以无源逆变，从而向无源网络供电，众多学者对柔性直流输电系统向无源网络供电进行了一系列的研究工作。文献[7]提出一种功率联合优化策略，实现了VSC-MTDC的可控输出与互联弱交流电网中措施之间的优化协调；文献[8]提出一种MMC-HVDC向海岛供电的有源/无源切换控制方法，能够实现海岛电网的平稳转换。目前对于无源网络通过MMC-HVDC接入大电网的机电暂态仿真研究仍未成熟，为对系统的稳定性进行研究，有必要建立 MMC-HVDC 的机电暂态模型[9]。文献[10]提出了一种混合多端直流输电系统的机电暂态建模策略，实现了交直流大电网的暂态稳定计算；文献[11]建立了一种考虑锁相环动态的柔直机电暂态模型；文献[12]提出了一种建立电压源型换流器和直流电网模型的实用方法，可用于大规模机电暂态仿真。

本文以dq坐标系下 MMC-HVDC 基频数学模型为基础，忽略MMC内部复杂的动态过程，仅保留无源系统及内外环控制器，建立了MMC-HVDC向无源网络供电时，无源侧机电暂态电压源模型；在忽略了内环控制器的动态过程后，建立了MMC-HVDC无源侧的机电暂态电流源模型。将两种模型与PSCAD中电磁暂态精确模型进行不同工况下的运行特性对比，验证了不同程度扰动下所建机电暂态模型的有效性;最后分析了内环控制器参数对于不同工况下两种机电暂态模型仿真结果产生的影响。

1 MMC-HVDC无源侧机电暂态建模

1.1 MMC数学模型

在机电暂态仿真中，由于柔性直流系统采用正序基波特性表示对于交流电网的作用，因此本文在研究换流器交流侧特性时，以交流系统三相对称，且只考虑基波分量为前提[13]。当通过柔性直流输电向无源网络供电时，系统结构如图1所示。其中MMC1、MMC2的直流侧相互连接，交流侧分别与有源网络、无源网络相连。MMCl工作在整流状态，将有功由有源网络传递给直流网络；MMC2工作在逆变状态，将有功和无功功率传递给无源网络[14]，图2为单个MMC拓扑结构图。

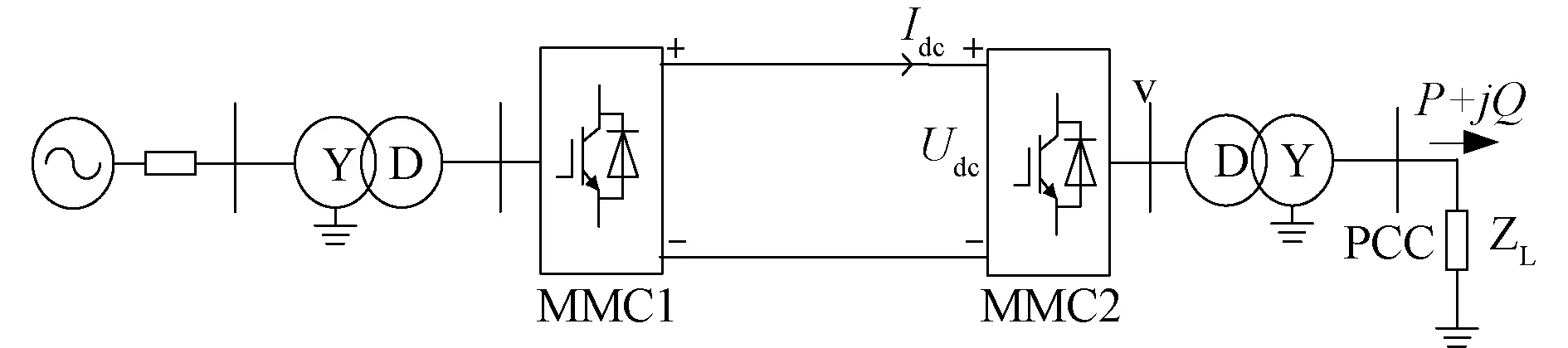
图1 MMC-HVDC向无源系统供电的系统结构图Fig. 1 System structure diagram of MMC-HVDC connected to passive network

图2 MMC拓扑结构图Fig. 2 Topological structure diagram of MMC

由于在研究换流器交流侧特性时仅考虑正序基波分量，因此采用MMC交流侧的基频动态数学模型进行机电暂态建模。为简化换流器的数学模型，采用派克变换将MMC-HVDC系统在三相坐标系下的正弦交流量转化为dq坐标系下的直流量，得到dq坐标系下的MMC数学模型如下[15]：

(1)

对dq坐标系下的MMC基频动态方程进行拉普拉斯变换，得到频域形式如下：

(2)

式中：L、R分别为PCC母线到换流器桥臂中点的等效电感与等效电阻；ud、uq分别表示PCC母线电压的d、q轴分量；ed、eq分别表示换流器上下桥臂电抗器虚拟等电位点电压的d、q轴分量；id、iq分别表示无源交流系统电流的d、q轴分量。

1.2 MMC控制器建模

柔性直流输电系统向无源网络供电时，送端换流器为MMC1，受端换流器为MMC2，MMC2的控制目标有两个，一是控制无源网络的频率为额定频率，二是控制无源网络PCC母线的电压幅值恒定；无源电网的频率为给定值，因此电角度θ=ω0t为确定值，控制系统也就不需要锁相环；此外，由于θ=ω0t给定，dq坐标系的旋转速度不变，若无源网络保持额定电压和频率，只需控制ud=Um、uq=0，考虑到换流器的过流能力，添加阀侧电流限幅环节，外环控制器的控制结构如图3所示[16]。

图3 外环控制器控制结构图Fig. 3 Control structure diagram of outer loop controller

内环控制器通过调节 MMC 的输出电压ed、eq使交流侧id、iq快速跟踪外环控制器输出的电流参考值idref、iqref，换流器采用电流解耦控制[17]，具体控制方式如图4所示。

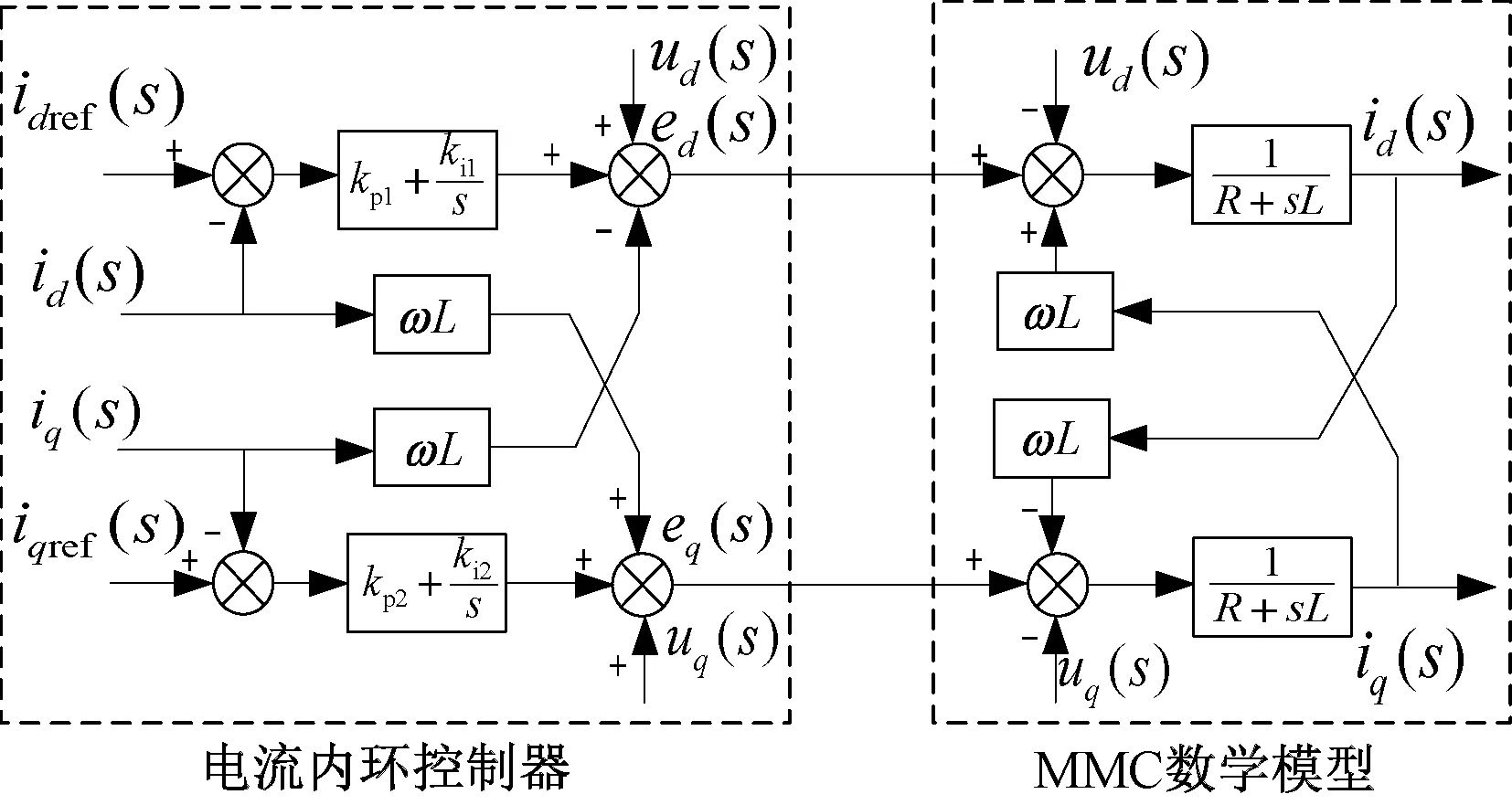
图4 内环电流控制器的输出电流跟踪控制框图Fig. 4 Output current tracking control block diagram of inner loop current controller

1.3 MMC-HVDC无源侧机电暂态模型

1.3.1 MMC-HVDC机电暂态电压源模型

对无源系统进行机电暂态仿真建模，忽略MMC内部复杂的动态过程，仅保留无源系统及内外环控制器，将换流站整体等效为受控电压源；为仿真实际系统的测量部份，对模型施加惯性环节，从而建立了MMC-HVDC无源侧机电暂态电压源模型，其具体结构框图如图5所示。

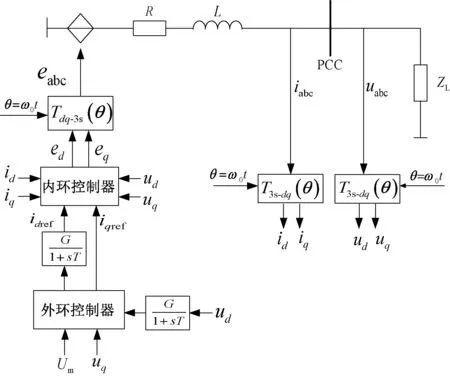
图5 MMC无源侧机电暂态电压源模型结构框图Fig. 5 Structure block diagram of MMC passive side electromechanical transient voltage source model

1.3.2 MMC-HVDC机电暂态电流源模型

根据内环电流控制器的控制框图可得到传递函数如下：

(3)

内环控制器的参数取值一般满足kp1>>L、kp2>>L(L为标幺值)，而传递函数Hd(s)、Hq(s)时域中表达式的时间常数含有2L/kp1、2L/kp2，机电暂态的仿真步长为ms级，因此内环电流控制器的动态过程理论上是可以忽略的[18]，即认为id、iq能够瞬时跟踪idref、iqref。

为增加模型的稳定性，对外环电压控制器的反馈输入量ud、uq和输出量idref、iqref分别施加一阶惯性环节[19]，由此可以得到无源侧的机电暂态电流源模型，该简化模型忽略了内环控制器，仅保留无源系统和外环控制器，将换流站等效为受控电流源，具体的结构框图如6所示。

图6 MMC无源侧机电暂态电流源模型结构框图Fig. 6 Structure block diagram of MMC passive side electromechanical transient current source model

2 MMC无源侧机电暂态仿真研究

2.1 算例介绍

本文对图1所示的单端有源MMC-HVDC 向无源网络供电系统进行仿真验证，其中 MMC1侧为送端，采用定直流电压控制和定无功功率控制，MMC2侧为受端，采用定频率控制和定交流电压控制，MMC的仿真系统参数与控制参数分别如表1、表2所示。

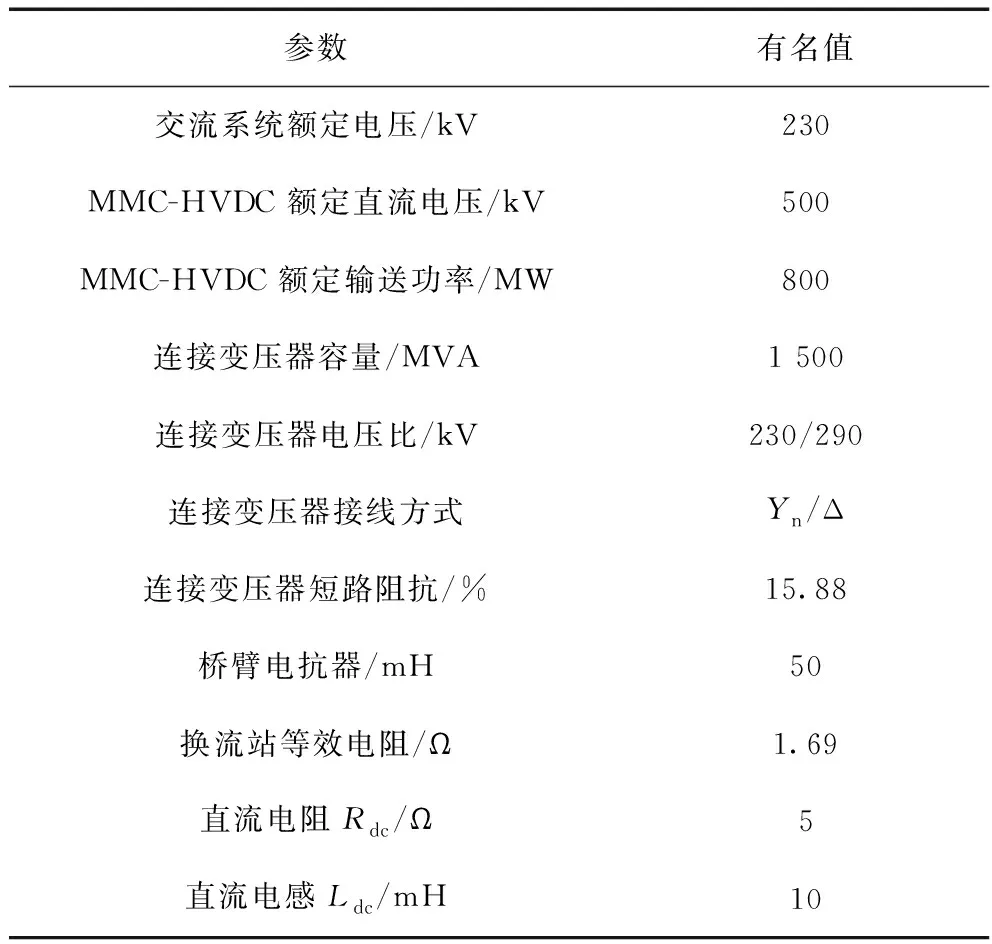
表1 MMC-HVDC仿真系统参数Tab.1 Parameters of MMC-HVDC simulation system

表2 MMC-HVDC控制参数Tab.2 Control parameters of MMC-HVDC

本文采用PSCAD作为MMC-HVDC 系统的电磁暂态模型和机电暂态模型仿真平台，采用带有内外限幅的PI控制器，且在电磁暂态和机电暂态仿真中采用相同的 PI 控制参数；为简化计算，对模型中的相关电气量进行标幺化处理。

2.2 系统仿真分析

2.2.1 小扰动下机电暂态模型仿真分析

无源系统原始负荷为800 MW，系统稳定运行1.0 s后，另外投入50 MW负荷，持续0.2 s 后切除。图7为无源系统在仿真过程中的动态变化。

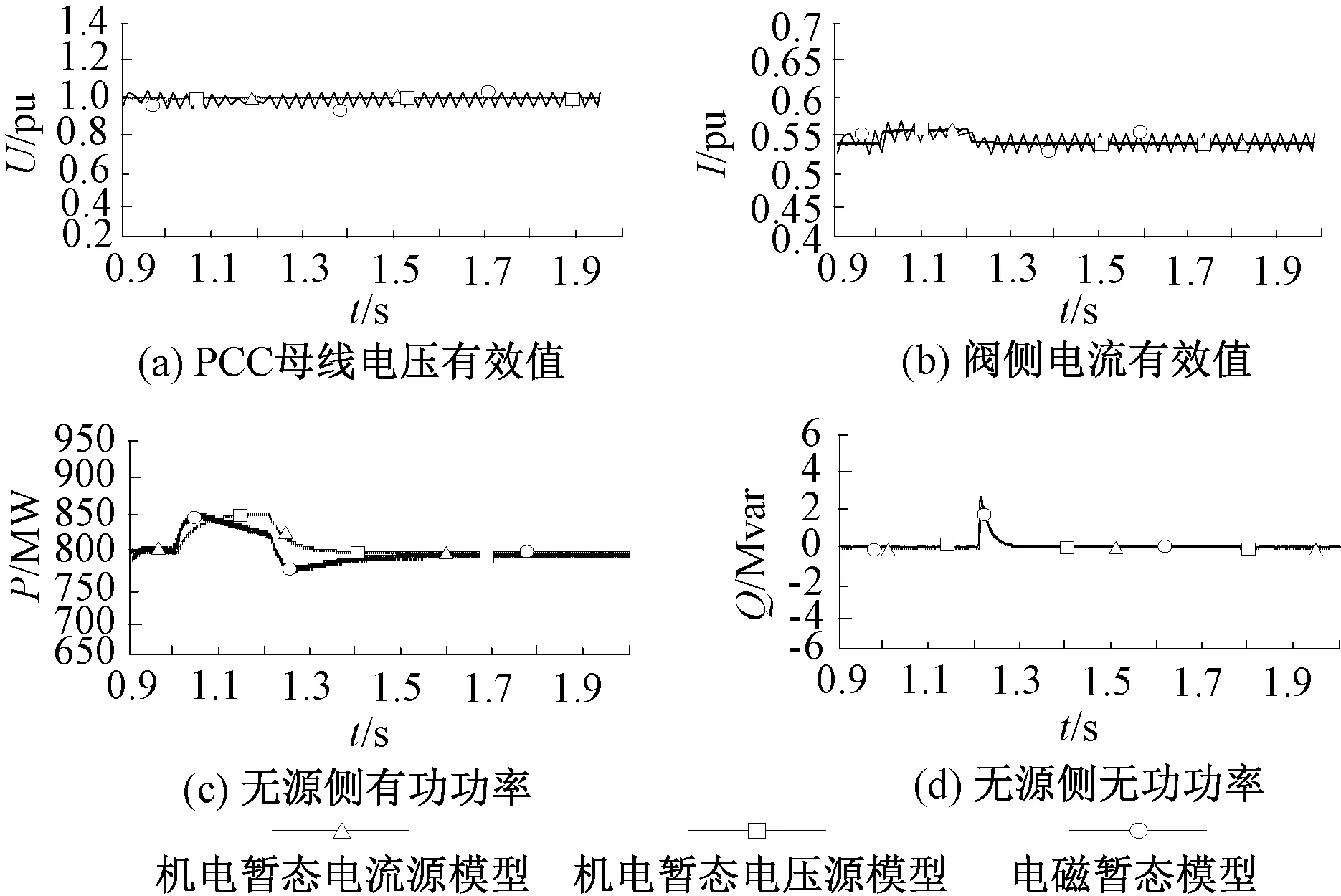
图7 小扰动下电磁、机电暂态模型的仿真结果对比Fig. 7 Comparison of simulation results of electromagnetic and electromechanical transient models under small disturbance

仿真结果表明，电磁暂态模型与两种机电暂态模型在小扰动下的动态过程基本一致，区别在于机电暂态模型只考虑了基波分量，而电磁暂态模型存在调制过程，因此含有一定的高频分量[20]；分析两种机电暂态模型，发现在对无源系统施加小扰动后，无论是电压源模型还是电流源模型，均能使无源系统PCC母线的电压和系统频率维持在给定值；随着有功负荷的投切，两种模型的有功随之变化，无功在切除故障的瞬间有微小变化，符合预期；除此之外，投入小负荷后，无源系统阀侧电流值增大，但未达到限幅、切除负荷后又恢复到原来数值。可以看出，小扰动下两种模型的仿真结果无太大差别，无源系统均能保持稳定。

2.2.2 大扰动下机电暂态模型仿真分析

无源系统原始负荷为800 MW，系统稳定运行1.0 s 后，PCC母线处发生三相金属性接地，持续0.2 s 后清除故障。图8为无源系统仿真过程中的动态变化。

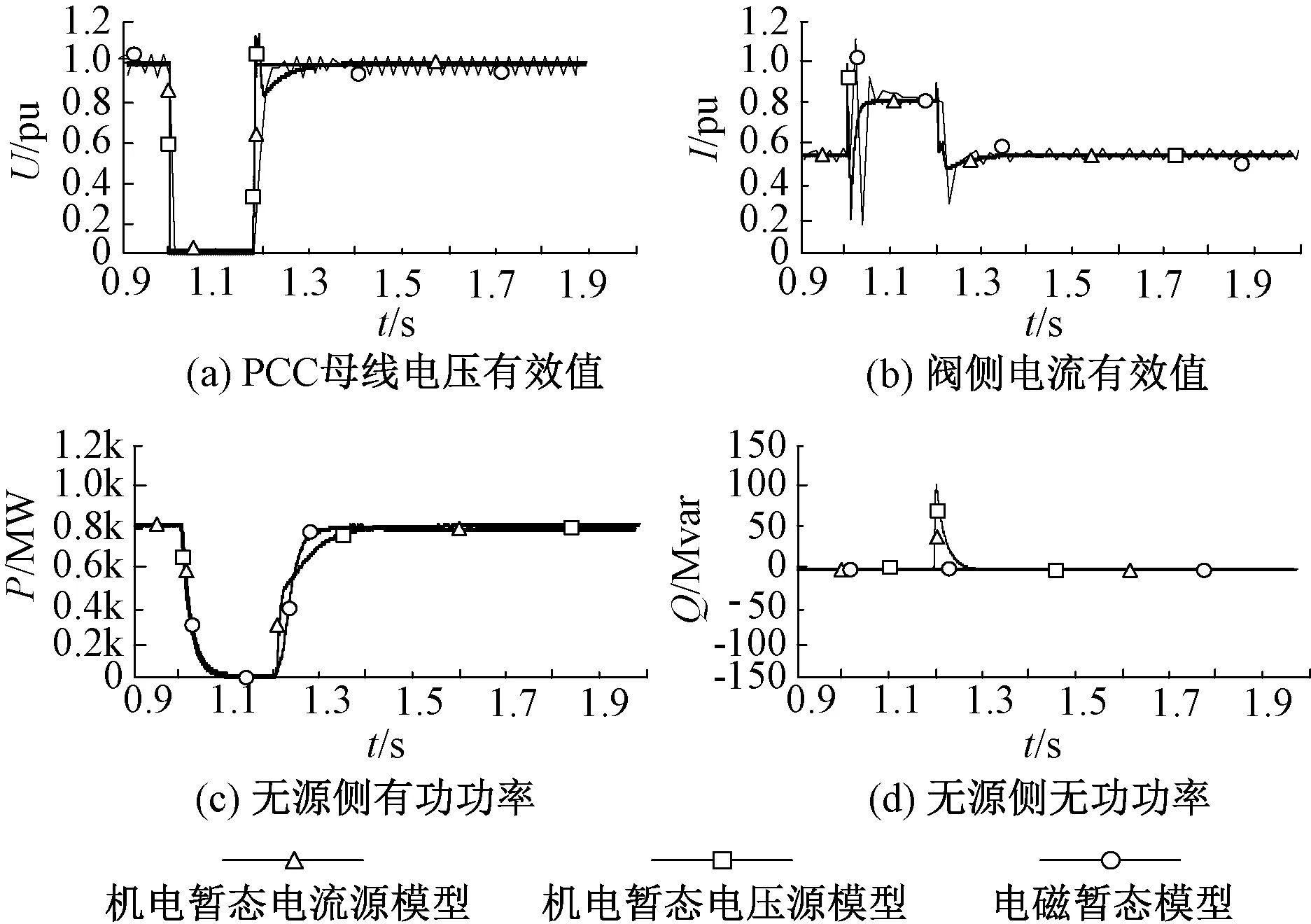
图8 大扰动下电磁、机电暂态模型的仿真结果对比Fig. 8 Comparison of simulation results of electromagnetic and electromechanical transient models under large disturbance

仿真结果表明，电磁暂态模型与两种机电暂态模型在大扰动下的动态过程大致相同，主要差别在于电磁暂态模型存在调制过程，含有一定的高频分量，而机电暂态模型只考虑了基波分量；分析电磁暂态模型，发现阀侧电流在短路的瞬间出现激增，超过了限幅值，之后电流先降后升，最终稳定在限幅值，在切除故障的瞬间电流骤降，大约100 ms后恢复到原来数值。

分析两种机电暂态模型，发现PCC母线处发生三相金属性接地后，电压源模型的无源系统PCC母线电压迅速下降为0,故障切除后的100 ms内，电压缓慢升高，100 ms后电压恢复到原控制值；阀侧电流在短路瞬间出现激增，超过了限幅值，但在10 ms后电流先降后升，最终稳定在限幅值，在切除故障的瞬间再次出现过流，之后电流先降后升，大约100 ms后恢复到原来数值。有功功率在故障后缓慢下降，100 ms后下降至0、故障切除后的200 ms内，有功缓慢升高，200 ms后恢复到原来水平；无功功率在故障切除后的20 ms内出现波动，与小扰动相比波动范围较大，之后迅速恢复为0。

电流源模型的仿真结果与电压源模型的仿真结果相近，但相较于电压源模型，无源系统的电气量在故障前后的响应速度更快，波形更加稳定平滑。尤其是阀侧电流，在故障施加和切除的瞬间未发生过限。

两种机电暂态模型对应的无源系统在大扰动下均能保持稳定，但电压源模型的仿真结果与电磁暂态精确模型的仿真结果更加一致；电流源模型与电压源模型相比更理想化，更强的体现了控制器的作用。

3 内环控制器参数对两种机电暂态模型的影响分析

本文的机电暂态电流源模型是在机电暂态电压源模型的基础上，忽略内环控制器的动态过程建立的，两种模型的本质区别在于是否保留内环控制器，因此有必要分析内环控制器参数对不同工况下两种机电暂态模型仿真结果产生的影响。

采用图1所示系统进行仿真分析，系统参数如表1所示，保持两种模型的外环控制器参数一致且不变，以上节机电暂态电流源模型的仿真结果作为对比，仅改变机电暂态电压源模型的内环控制器参数。仿真发现，当对无源系统施加小扰动时，改变内环控制器参数kp只会对电压源模型中无源系统电气量的响应速度造成影响，当kp变化不大时，电压源模型的仿真结果无太大差别，无源系统均能保持稳定，此时两种模型的仿真结果基本一致，具体如图9所示。

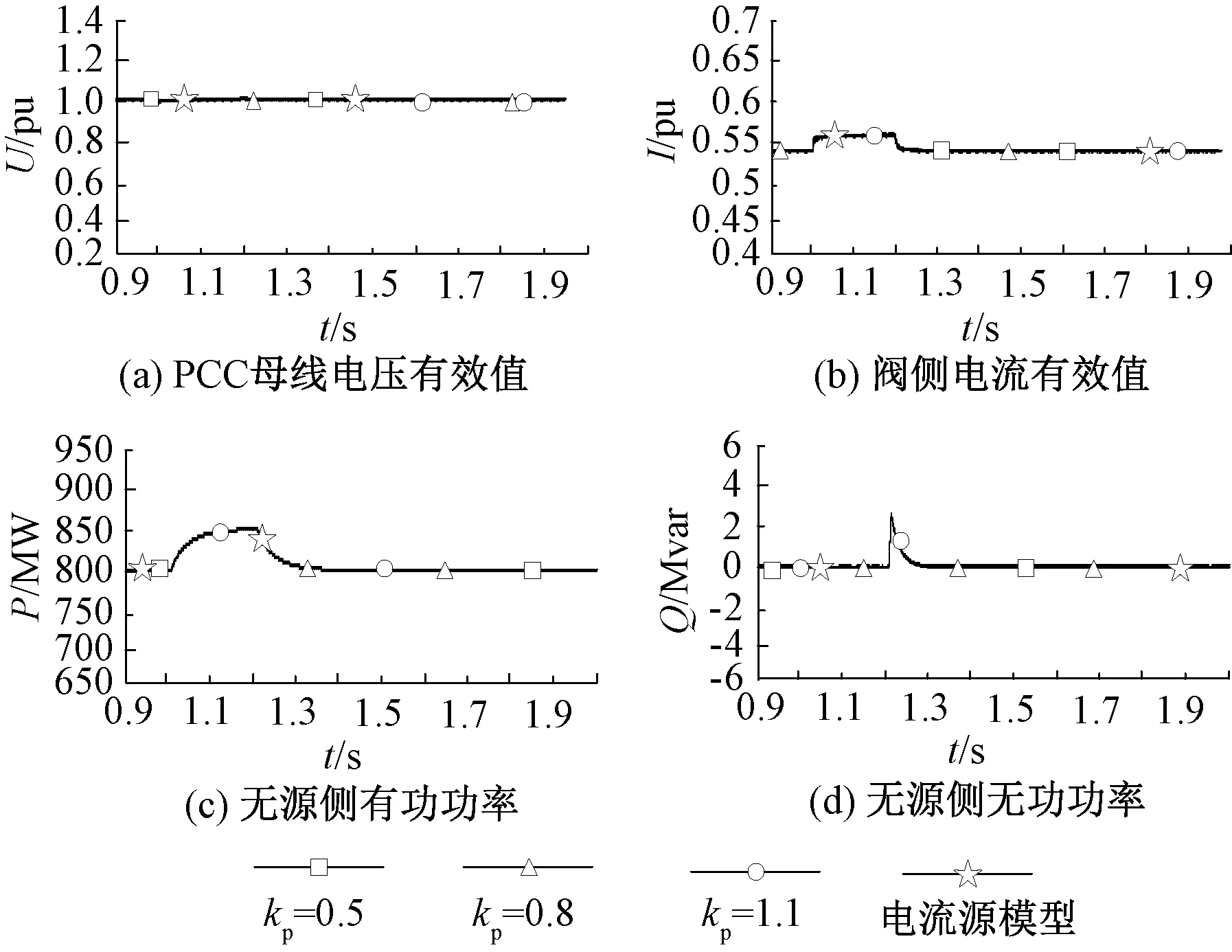
图9 内环控制器取不同参数的小扰动仿真结果对比Fig. 9 Comparison of small disturbance simulation results of inner loop controller with different parameters

当对无源系统施加大扰动时，在相同范围内改变内环控制器参数kp、此时有可能造成阀侧电流过限，电压源模型与电流源模型得到的仿真结果可能不再一致，具体如图10所示。

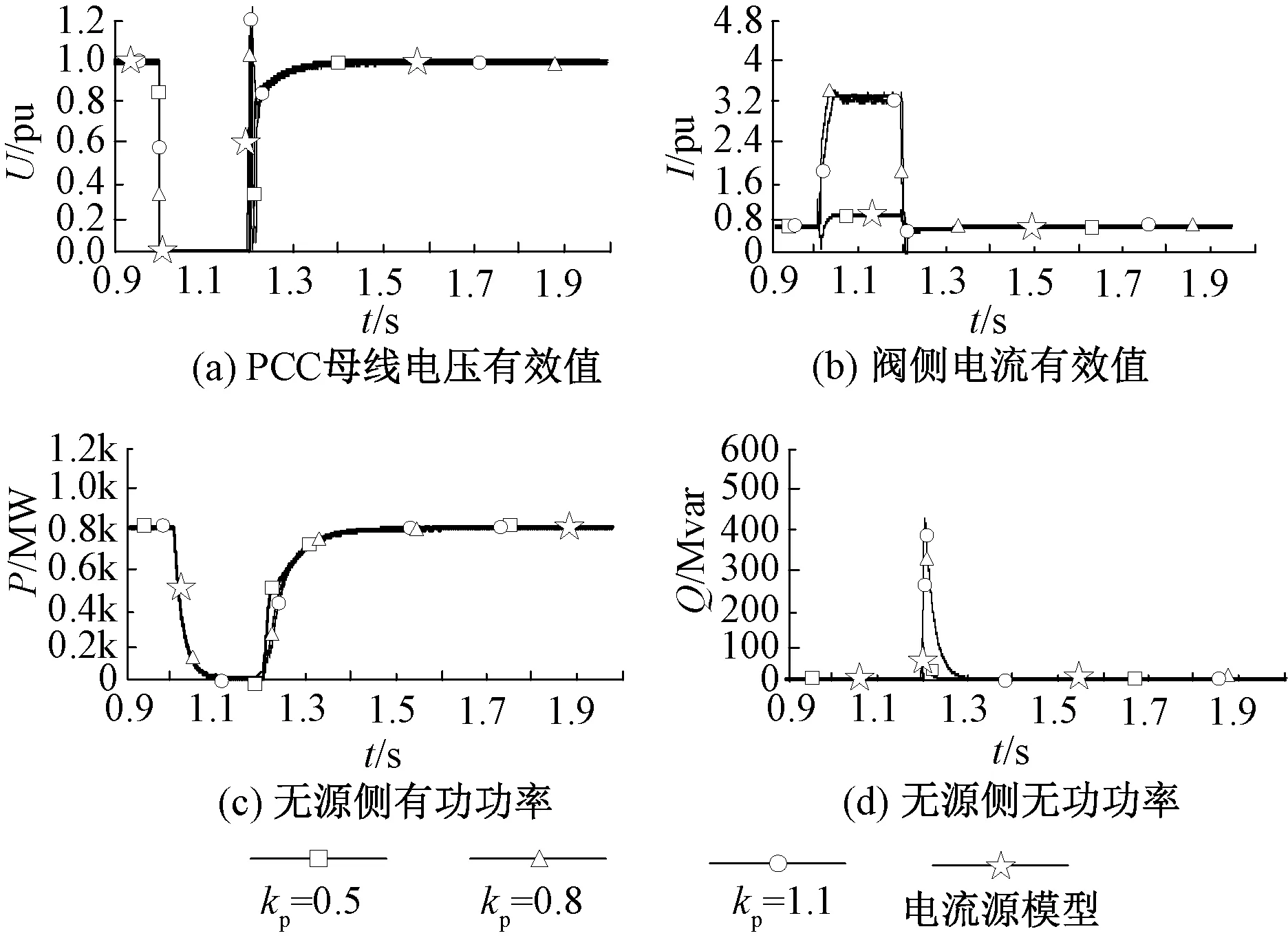
图10 内环控制器取不同参数的大扰动仿真结果对比Fig. 10 Comparison of large disturbance simulation results of inner loop controller with different parameters

分析可知，尽管两种模型都存在阀侧电流的限幅环节，但机电暂态电流源模型外环输出的电流参考值直接作为系统的控制输入量，而机电暂态电压源模型的外环输出量要作为内环控制器的给定值，系统实际的控制输入量为内环控制器输出的ed、eq，当对无源系统施加大扰动时，由于外环控制器的输出idref、iqref很快达到限幅值，若内环控制器的参数kp超出一定范围，内环PI控制器输出很容易讯速达到限幅值，此时电流限幅环节无法再起作用，导致阀侧电流过限。

仿真结果表明，若机电暂态电压源模型与电流源模型的外环控制器参数相同，当对无源系统施加小扰动时，改变机电暂态电压源模型的内环控制器参数，对电压源模型的仿真结果影响较小，此时两种模型的仿真结果基本一致；但当对无源系统施加大扰动时，机电暂态电压源模型的稳定性对于内环参数的变化十分敏感，在相同范围内改变内环控制器kp参数，电压源模型的仿真结果变化较大，两种机电暂态模型的仿真结果可能不再一致，因此需要结合正确的工程参数进行机电暂态建模。

4 结 论

本文提出了MMC-HVDC向无源网络供电时、无源侧的机电暂态仿真模型。忽略MMC内部复杂的动态过程，根据是否保留内环控制器，先后建立了无源侧机电暂态电压源模型与机电暂态电流源模型；以电磁暂态精确模型仿真结果为对比，对不同扰动下两种机电暂态模型进行了仿真分析；研究了内环控制器参数对于不同工况下两种机电暂态模型仿真结果的影响，得到结论如下：

(1) 当对无源系统施加小扰动时，电磁暂态模型与两种机电暂态模型在小扰动下的动态过程基本一致，均符合控制要求；因此在对MMC-HVDC向无源网络供电进行小扰动下的机电暂态建模时，既可采用电压源模型，也可采用电流源模型。

(2) 当对无源系统施加大扰动时，电磁暂态模型和两种机电暂态模型仿真结果相似，电压源模型的仿真结果与电磁暂态精确模型的仿真结果更加符合，而电流源模型的仿真结果更趋于理想化。因此在对MMC-HVDC向无源网络供电进行大扰动下的机电暂态建模时，考虑到模型应更真实的反应实际系统的运行特性，应采用电压源模型。

(3) 机电暂态电压源模型和电流源模型的本质区别在于是否保留内环控制器，改变内环控制器参数，两种机电暂态模型的仿真结果可能不再一致，而且无源系统受到的扰动程度不同，使两种机电暂态模型仿真结果保持一致的kp范围也不同，小扰动下kp范围大，大扰动下kp范围小。由于机电暂态电压源模型的稳定性对于内环参数的变化较为敏感，因此需要结合正确的工程参数进行机电暂态建模。