光伏经LCC-HVDC外送系统的次同步振荡特性分析

2022-04-08高本锋陈淑平邵冰冰赵书强

华北电力大学学报(自然科学版) 2022年2期

高本锋，陈淑平，沈琳，刘毅，邵冰冰，赵书强

(1.河北省分布式储能与微网重点实验室(华北电力大学)，河北保定 071003；2.电网安全与节能国家重点实验室(中国电力科学研究院有限公司)，北京 100192)

0 引言

截至2020年9月，全国光伏累计装机容量2.23亿千瓦[1]；在“30·60”碳目标提出后，光伏爆发式增长的态势近在咫尺。由于我国太阳能能源具有分布集中度高、与负荷中心呈逆向分布的特点，光伏发电需通过远距离传输以提高能源消纳能力，其中西北地区的大规模光伏主要经电网换相高压直流(line-commutated-converter based high voltage direct current，LCC-HVDC)输电系统外送[2-4]。据统计，我国在运在建的光伏外送特高压直流工程共7项。LCC-HVDC在规模化光伏外送方面具有广阔的应用前景。

现有的LCC-HVDC工程，已有整流站建设在光伏电站附近，如青海-河南±800kV特高压直流工程。随着光伏的迅猛发展，未来可能出现更多光伏电站位于送端近区的情况。由于光伏自身存在弱阻尼的次同步振荡(sub-synchronous oscillation, SSO)模式[5]，对于此种光伏电站离LCC-HVDC整流站电气距离较小的场景，二者间的动态交互作用可能会削弱SSO模式阻尼，从而增大系统发生SSO的风险。因此，当光伏电站位于LCC-HVDC整流站近区时，它们之间的动态交互作用不可忽视，对此开展相关研究具有实际工程意义。

限于现有技术和网架结构，光伏主要通过交流电网和LCC-HVDC两种方式外送。目前，针对光伏外送系统SSO问题的研究多集中于光伏电站接入弱交流电网，较少涉及LCC-HVDC。文献[6]对电力电子化电力系统中的振荡问题进行了探讨，研究表明光伏电站在接入弱交流电网时存在振荡失稳的风险。文献[7,8]指出包含光伏电站的并网微电网系统在公共耦合点处有次同步电流分量。文献[9]基于阻抗分析法对光伏并入弱交流电网的SSO机理和参数特性进行了深入分析。文献[10-12]采用了特征值分析法研究了光伏发电系统的SSO特性。文献[13,14]以弱交流电网接入为背景，对多光伏逆变器并联系统的稳定性问题展开研究。由此可知，光伏经弱交流电网并网存在发生SSO的风险，而对于光伏经LCC-HVDC外送是否会发生SSO尚无定论，国内外相关研究基本空白。

目前关于新能源经LCC-HVDC外送系统的SSO问题分析主要集中于风电，较少涉及光伏。文献[15,16]分别基于近似强谐振理论和系统闭环互联传递函数框图对直驱风电机组经LCC-HVDC外送系统的SSO机理进行分析。文献[17]采用特征值法对双馈风电场经LCC-HVDC外送系统的SSO特性展开研究，分析了系统参数对稳定性的影响。然而，由于光伏与风电在拓扑结构和控制策略上存在较大差异，LCC-HVDC与两种电源的耦合关系不同，现有文献针对风电的研究结论对光伏参考价值有限。

综上所述，当前研究大多集中于光伏电站接入弱交流电网和风电场经LCC-HVDC外送系统的SSO问题，尚无涉及光伏电站经LCC-HVDC外送系统的SSO问题分析，对于LCC-HVDC接入对系统SSO的影响更是尚属空白。因此，有必要结合工程实际，对光伏经LCC-HVDC外送系统的SSO特性进行分析。

目前针对新能源与LCC-HVDC间SSO问题的研究方法，主要采用特征值分析法和阻抗分析法[18，19]。特征值分析法作为一种准确且严格的线性系统理论分析方法，能够有效地提供研究对象的特征信息，因此该方法可用于光伏经LCC-HVDC外送系统SSO特性的分析[20]。由于研究系统较为复杂，涉及变量较多，本文采用模块化建模方法来建立状态空间模型。模块化建模法只需对系统中各基本单元进行建模，克服了传统特征值法建模时计算量和难度较大、灵活性差且出错率高的缺点，大幅降低了建模难度。

本文采用特征值分析与时域仿真验证相结合的方法，研究光伏经LCC-HVDC外送系统的SSO模式以及系统参数对SSO阻尼的影响。首先，基于模块化建模建立光伏经LCC-HVDC外送系统的60阶状态空间模型，并与时域仿真模型进行阶跃响应特性对比，验证状态空间模型的准确性；其次，采用特征值法对系统的SSO模式进行分析，研究LCC-HVDC接入对系统SSO模式的影响；最后，根据参与因子分析结果，通过特征值根轨迹分析系统参数对SSO特性的影响。

1 光伏经LCC-HVDC外送系统结构

图1为光伏经LCC-HVDC外送系统结构示意图。为便于分析，将整个系统划分为送端交流系统、受端交流系统、光伏电站和LCC-HVDC四部分。其中光伏电站子系统包括光伏电站及其与送端交流系统相连的输电线路部分；LCC-HVDC子系统包括LCC-HVDC输电系统及其配套交流滤波器组。光伏电站和送端交流系统并联在同一条母线上，二者的功率通过LCC-HVDC送至受端交流系统。系统主要参数如表1所示。

表1 研究系统主要参数Tab.1 Main parameters of research system

图1中各变量定义如下：在光伏电站子系统中，ipv、Udc分别为光伏阵列端口输出电流和电压，C、in分别为直流侧电容和电流，ut、it分别为逆变器输出电压和线路电流，ug、ig分别为一级升压变低压侧电压和电流，il为光伏电站输电线路电流；在LCC-HVDC子系统中，ur、ir分别为整流侧母线电压、线路电流，ui、ii分别为逆变侧母线电压、线路电流，Udcr、Idcr分别为整流侧直流电压、电流，Udci、Idci分别为逆变侧直流电压、电流；在交流系统中，uac1、iac1分别为送端交流系统电压、电流，uac2、iac2分别为受端交流系统电压、电流。

图1中光伏电站容量为210MW，由150台额定容量为1.4MW的光伏发电单元聚合而成。研究表明，当新能源并网系统发生SSO时，新能源系统作为一个整体与电网进行动态交互，因此在研究新能源并网系统的SSO问题时，基于聚合等值模型的分析结果仍具有重要的参考价值[9,21，22]。光伏发电单元采用典型的单级式拓扑[23]，光伏并网逆变器控制策略采用基于电压定向的矢量控制策略，其中控制器外环采用定直流电压控制策略及单位功率因数控制策略，控制参数见附录表A1。LCC-HVDC采用国际大电网会议(CIGRE)提出的高压直流输电标准模型[24]，控制参数见附录表A2。

表A1 光伏并网逆变器控制参数Tab.A1 Control parameters of photovoltaic grid-connected inverter

表A2 LCC-HVDC控制器参数Tab.A2 Parameters of LCC-HVDC controller

图1 光伏经LCC-HVDC外送系统的结构示意图Fig. 1 Structure diagram of the photovoltaic power integrated to LCC-HVDC system

鉴于本文重点研究光伏电站经LCC-HVDC外送系统的SSO特性，即研究场景中光伏电站距离整流站较近，而火电机组距离整流站较远，且受端交流系统仅与逆变侧相连，对所研究的光伏电站与LCC-HVDC间的动态交互影响较小。因此，根据戴维南定理将送、受端交流系统等效为等值电压源(Sac1、Sac2)及其等值阻抗(Rac1+jXac1、Rac2+jXac2)。

2 光伏经LCC-HVDC外送系统的状态空间模型

鉴于研究系统的复杂性，采用模块化建模法来建立系统状态空间模型，并与时域仿真模型进行阶跃响应特性对比，验证所建立状态空间模型的有效性。

2.1 系统数学模型

由于篇幅限制，本节不再详述光伏经LCC-HVDC外送系统各部分数学模型，仅对基于模块化建模方法形成状态空间模型的过程进行阐释。光伏电站的数学模型可参考文献[11,25]，交流系统和LCC-HVDC的数学模型可参考文献[26-27]。

2.2 状态空间模型建立

传统特征值建模方法具有计算难度大、出错率高和灵活性差的缺点，考虑到光伏经LCC-HVDC外送系统较为复杂，本节采用更为简便的模块化建模方法来建立状态空间模型[28，29]。模块化建模法将研究系统细分成不同的模块，线性化各模块的微分方程，并通过联接矩阵建立连接，从而得到整个研究系统的状态空间模型。采用模块化建模方法建立光伏经LCC-HVDC外送系统步骤如下：

(1)对复杂研究系统进行分块

模块化建模法的优势在于仅需要对各模块的状态空间模型进行解析推导，从而大大降低了建模难度，因此如何对复杂研究系统进行分块是模块化建模法需要重点关注的问题。

图1将整个系统划分为送端交流系统、受端交流系统、光伏电站和LCC-HVDC四部分，本节进一步对子系统进行细分：将光伏电站细分成光伏阵列模块、直流侧电容模块、逆变器模块、锁相环模块、滤波器模块和输电线路模块；将LCC-HVDC细分成直流线路模块、换流器模块(包括定电流控制器模块和定关断角控制器模块)、锁相环模块和交流滤波器模块。

(2)各模块状态方程和输出方程线性化

建立各模块的状态空间模型，即在稳态运行点对各模块状态方程和输出方程线性化，并根据模块间的输入输出关系确定各模块的输入输出变量，得到状态空间模型。模块k的状态空间模型如式(1)所示。

(1)

式中：Ak、Bk、Ck、Dk是模块k的系数矩阵，其值与系统的稳态运行点有关；Xk、Uk和Yk分别为该模块的状态变量矩阵、输入变量矩阵和输出变量矩阵。

(3)坐标系选取及坐标变换方程

本文研究系统涉及3种不同的坐标系：交流系统在与电压源A相电压同步的xy坐标系下建模，光伏电站在dq坐标系下建模，LCC-HVDC在极坐标系下建模。为建立起各子系统间的联系，需要对各子系统端口的连接变量进行坐标变换，因此光伏电站端口的dq分量和LCC-HVDC端口的幅值相角分量均需要向交流系统端口的xy分量进行转换，3种坐标系的转换关系如图2所示。

图2 系统涉及坐标系的转换关系Fig. 2 Transformation relation of system coordinate system

任意变量α在xy坐标系和dq坐标系之间的转换关系满足式(2)。任意变量β在xy坐标系和极坐标系之间的转换关系满足式(3)。

(2)

(3)

式中：θpll为变量α对应锁相环的输出角度；ψ为变量β对应的相角。

(4)形成全系统状态空间模型

通过步骤(1)对研究系统进行模块划分，步骤(2)建立各模块的状态空间模型，各模块的连接情况以及端口输入输出量如图3所示。采用MATLAB/Simulink搭建图3所示的状态空间方程模型，通过步骤(3)对各子系统建立连接，经过运算可生成所研究系统的60阶状态空间模型，如式(4)所示。

图3 光伏经LCC-HVDC外送系统接口图Fig. 3 Interface diagram of the photovoltaic power integrated to LCC-HVDC system

(4)

式中：X为状态变量，U为输入变量。全系统状态空间模型共包含60个状态变量，按照其所属模块可以分为15个组，如表2所示。其中，状态变量X=[Xdc,XPVF,Xpll1,XC,XN,XRL,XDC,XACF2,Xpll3,XI,XR,XACF1,Xpll2,Xac1,Xac2]T，输入变量U=[Udcref,igqref,Idcref,γref]T。

表2 状态变量分组Tab.2 Grouping of state variables

2.3 状态空间模型的准确性验证

本节对比状态空间模型与时域仿真模型的阶跃响应曲线，以验证所形成状态空间模型的准确性。基于第1节列出的系统结构与运行参数，在PSCAD/EMTDC时域仿真平台中搭建对应的电磁暂态仿真模型，并于5.0 s时刻设置光伏电站直流电压指令值Udcref阶跃，阶跃幅值为0.05 kV，其它参考值保持不变。MATLAB模型与PSCAD/EMTDC模型的阶跃响应特性对比结果如图4所示。图4(a)-(e)分别为光伏阵列输出电流Ipv、光伏电站直流电容C电压Udc、网侧电流d轴分量Igd、网侧电压q轴分量Ugq、LCC-HVDC整流侧电流Idcr的阶跃响应曲线。

由图4(a)～(e)可知，状态空间模型的动态响应与PSCAD/EMTDC模型的时域仿真结果基本一致，对比结果验证了状态空间模型的准确性。

图4 阶跃响应曲线Fig. 4 Step response curve

3 光伏经LCC-HVDC外送系统的SSO模式

本节基于第2节搭建的模型，研究光伏经LCC-HVDC外送系统的SSO特性。采用特征值分析法确定系统的振荡模式，并从SSO模式的相关状态变量出发，分析是否存在光伏电站与LCC-HVDC共同参与的SSO模式，并研究LCC-HVDC接入对系统SSO阻尼的影响。

3.1 振荡模式

对第2节所建立的状态空间模型进行特征值求解，由求解得到的特征值结果可知，系统中存在高频振荡、低频振荡和SSO振荡三类振荡。本节仅考虑阻尼较小的振荡模式，按照振荡类型选取特征值结果如表3所示。

表3 特征值结果Tab.3 Eigenvalue result

由表3可知，研究系统中的振荡模式有1个高频振荡模式(λ1,2)，4个SSO模式(λ3,4、λ5,6、λ7,8、λ9,10)和1个低频振荡模式(λ11,12)。其中模式4对应的特征值λ7,8=8.01±j101.22实部为正，该模式是一对不稳定的SSO模式，为系统的主导振荡模式，振荡频率为16.11 Hz。

对上述特征值分析结果进行仿真验证，在PSCAD/EMTDC模型中进行相同工况下的仿真，4.0 s打开图1中所示开关K，从而在线路中串联电感L0，直流电容电压的PSCAD/EMTDC时域仿真波形如图5所示。

图5 相同工况下的电容电压曲线和FFT分析结果Fig. 5 Capacitor voltage curve and FFT analysis results under the same working condition

由图5可知，4.0 s前，光伏经LCC-HVDC外送系统稳定运行；4.0 s后，线路中串入电感，阻尼为负，系统发生了主导频率为16 Hz的SSO，与表3中的正实部特征根相对应。由上述分析结果可知，当光伏经LCC-HVDC送出时，存在发生不稳定SSO的风险，验证了基于特征值分析法推导结果的准确性。

3.2 参与因子分析

参与因子能够准确反映系统状态变量和振荡模式之间的关系[20]，常用来研究状态变量在模式中的参与程度。参与因子越大，状态变量和模式之间的联系越紧密。因此，本节通过参与因子对各SSO模式的相关变量进行分析。

表3中6种模式的参与因子分析结果如图6所示。图6中横坐标表示状态变量，纵坐标表示各状态变量在该模式中的参与程度。

图6 参与因子分析Fig. 6 Participation factors analysis

由图6(a)可知，模式1的强相关状态变量为光伏电站滤波器XPVF，是光伏电站LCL滤波器引入的振荡，该模式是仅由光伏电站的状态变量参与的高频振荡模式。

由图6(b)～(d)可知，与模式2～4相关的状态变量为光伏电站直流电容环节Xdc、锁相环Xpll1、并联电容XC、逆变器控制XN、输电线路XRL、LCC-HVDC直流输电线路XDC、整流侧换流器控制XR、送端交流电源Xac1和受端交流电源Xac2，模式2～4是由光伏电站、LCC-HVDC和交流系统共同参与的SSO模式。

由图6(e)可知，模式5的主导参与变量为LCC-HVDC直流输电线路XDC、整流侧换流器控制XR和送端交流电源Xac1，该模式是由LCC-HVDC与交流系统的状态变量共同参与的SSO模式。

由图6(f)可知，模式6由LCC-HVDC整流侧锁相环Xpll2和逆变侧锁相环Xpll3主导参与，是由LCC-HVDC锁相环引入的振荡，该模式是仅由LCC-HVDC的状态变量参与的低频振荡模式。

由参与因子分析可知，模式2-4是由光伏电站和LCC-HVDC的状态变量共同参与的振荡，其中模式4为不稳定的振荡，对系统的稳定性影响最大。模式4与光伏电站直流电容环节Xdc、并联电容XC、输电线路XRL、逆变器控制XN、LCC-HVDC直流输电线路XDC、整流侧换流器控制XR、送端交流电源Xac1和受端交流电源Xac2相关，其中Xdc的参与程度最高，可知模式4是由光伏电站直流电容主导，整流侧换流器控制以及交流系统共同参与的SSO模式。结合系统结构及相关状态变量，光伏经LCC-HVDC外送系统的SSO机理可以解释为：由于公共耦合点的存在，耦合点处的电压、电流相互驱动，导致光伏与LCC-HVDC间形成次同步交互作用，进而对光伏经LCC-HVDC外送系统的SSO产生影响。

综上，当系统参数不合适时，光伏经LCC-HVDC外送系统有发生SSO的风险，公共耦合点电压、电流扰动相互驱动的动态过程导致光伏与LCC-HVDC间形成次同步交互作用，使得系统中存在光伏电站和LCC-HVDC的状态变量同时参与的振荡模式。

3.3 LCC-HVDC对系统SSO阻尼的影响

现有文献多采用2工况对比方法以实现新能源并网系统中子系统间的交互作用分析[17,30，31]。因此，本节分别设置接入LCC-HVDC、不接入LCC-HVDC工况，通过对2种工况下的状态空间模型进行特征值分析，研究LCC-HVDC对光伏并网系统SSO阻尼的影响。其中接入LCC-HVDC的状态空间模型为第2节搭建的光伏经LCC-HVDC外送系统模型，采用了详细LCC-HVDC模型；不接入LCC-HVDC的状态空间模型为光伏并网系统模型，该模型忽略了LCC-HVDC的动态特性，采用恒流源代替LCC-HVDC模型，以保持系统潮流不变。此外，本节仅对比对系统稳定性影响较大的主导振荡模式，接入LCC-HVDC工况下系统的主导振荡模式为3.2节中的模式4，不接入LCC-HVDC工况下系统的主导振荡模式为模式7；值得注意的是，模式4与模式7的参与变量并不完全相同，模式7是由光伏电站和交流系统共同参与的SSO模式。两种工况下主导振荡模式的特征值结果如表4所示。

表4 接入/不接入LCC-HVDC工况下的特征值结果

由表4可知，接入LCC-HVDC会导致主导振荡模式的实部增大，稳定性变差，即LCC-HVDC会加剧SSO。

为验证上述理论分析结果的正确性，在PSCAD/EMTDC中按照图1所示结构搭建光伏经LCC-HVDC外送系统的仿真模型，对比接入LCC-HVDC与不接入LCC-HVDC两种工况下振荡幅度的大小。为保证系统潮流保持不变，在不接入LCC-HVDC的仿真模型中采用以恒流源代替LCC-HVDC的光伏并网系统模型。在接入LCC-HVDC的工况下启动仿真，4.0 s时打开开关K，在线路中串联电感L0以激发振荡，5.5 s时使LCC-HVDC退出运行同时接入恒流源，此时系统切换为不接入LCC-HVDC的工况。两种工况下光伏电站直流电容电压Udc的时域仿真波形如图7所示。

图7 接入/不接入LCC-HVDC工况下的直流电容电压Fig. 7 DC capacitor voltage curve with/without LCC-HVDC operating conditions

由图7可知，4.0 s～5.5 s时，由于线路中串入电感，系统发生SSO；在5.5 s时恒流源代替LCC-HVDC，振荡幅值迅速减小。时域仿真结果表明LCC-HVDC接入会削弱SSO模式的阻尼，增大振荡幅值，即验证了表4特征值分析结果。

因此，光伏经LCC-HVDC外送系统存在光伏与LCC-HVDC共同参与的SSO模式；且LCC-HVDC的接入为光伏并网系统SSO模式提供负阻尼，加剧了振荡，不利于系统的稳定。

4 影响因素分析

由3.2节的参与因子分析结果可知，系统SSO模式与LCC-HVDC整流侧控制器参数、光伏电站的逆变器控制参数和直流侧电容值相关。本节据此选取影响因素，分析上述参数变化对光伏经LCC-HVDC外送系统SSO特性的影响。由于模式4为不稳定的振荡模式，主要对其进行分析。

4.1 LCC-HVDC整流侧控制器参数

对系统状态空间模型进行特征值根轨迹分析，各参数与表1、附录表1、2保持一致，其它影响因素的工况设置与此处一致。当整流侧控制器比例系数Kpdc或积分系数Kidc变化时，模式4的特征值根轨迹如图8所示。图8(a)、(b)分别为LCC-HVDC整流侧控制器的比例系数Kpdc由0.25Kpdc0增加至4.0Kpdc0时、积分系数Kidc由0.1Kidc0增加至1.0Kidc0时模式4的特征值根轨迹曲线。

图8 整流侧控制器参数的影响Fig. 8 Influence of control parameter variation of rectifier

由图8(a)可知，随着Kpdc的增大，模式4的特征值逐渐向左移动，特征值实部减小，系统的阻尼增大，稳定性不断增强；特征值虚部不变，系统SSO频率不发生改变。由图8(b)可知，随着Kidc的增大，模式4的特征值逐渐向右移动，特征值实部增大，系统的阻尼减小，稳定性不断减弱；特征值虚部不变，系统SSO频率不发生改变。

在PSCAD/EMTDC中对上述理论分析结果进行时域仿真验证，设置仿真工况如下：4.0 s时刻，打开图1开关K，在线路中串联电感L0以引发SSO，其它影响因素的仿真工况设置与此处一致。图9所示为不同整流侧控制器参数下，直流电容电压Udc的时域仿真曲线对比图。图9(a)、(b)分别为整流侧控制器的比例系数Kpdc为0.5Kpdc0、1.0Kpdc0、2.0Kpdc0时、积分系数Kidc为0.1Kidc0、0.2Kidc0、1.0Kidc0时直流电容电压Udc的时域仿真曲线。

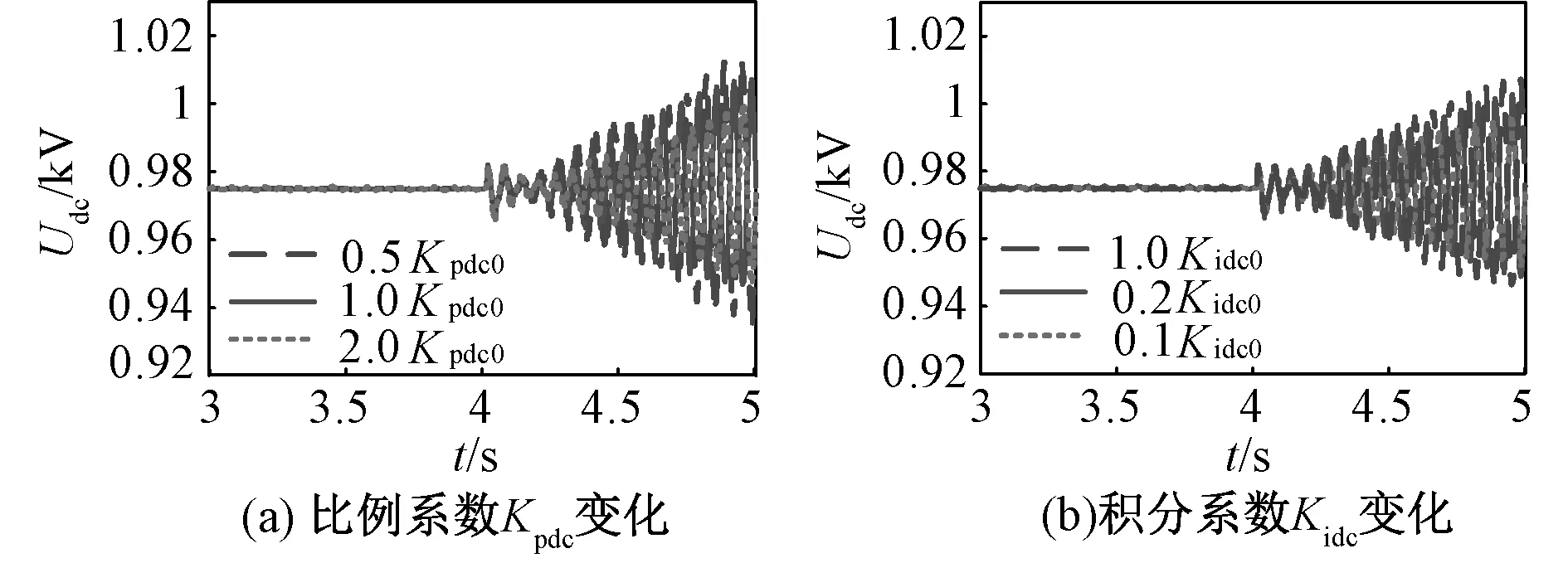
图9 直流电容电压Udc 曲线(整流器控制参数变化)Fig. 9 DC capacitor voltage curve (Rectifier control parameters change)

由图9(a)可知，随着Kpdc的增大，系统的阻尼增大，Udc的振荡幅度减小，系统SSO的频率不发生改变。由图9(b)可知，随着Kidc的增大，系统的阻尼减小，Udc的振荡幅度增大，系统SSO的频率不发生改变。

特征值根轨迹和时域仿真结果均表明，在一定参数范围内，增加Kpdc和减小Kidc均可增加系统的稳定性，提高系统对SSO的阻尼，减小系统发生SSO的风险。

4.2 光伏电站的逆变器外环控制参数

当光伏并网逆变器外环比例系数Kppv由0.5Kppv0增加至2.0Kppv0时，模式4的特征值根轨迹如图10所示。

图10 逆变器控制参数的影响Fig. 10 Influence of control parameter variation of inverter

由图10可知，随着Kppv的增大，模式4的特征值逐渐向左移动，特征值实部减小，系统的阻尼增大，稳定性不断增强；特征值虚部增大，系统SSO频率增加。此外，对比图8(a)和图10可以发现，相较于LCC-HVDC整流侧控制器参数，光伏电站逆变器外环控制参数改变时特征值实部变化的幅度更大，对模式4的影响更大。

在PSCAD/EMTDC中对上述理论分析结果进行时域仿真验证，当光伏电站并网逆变器外环比例系数Kppv为0.5Kppv0、1.0Kppv0、2.0Kppv0时，直流电容电压Udc的时域仿真曲线如图11所示。

图11 直流电容电压Udc曲线(逆变器控制参数变化)Fig. 11 DC capacitor voltage curve (Inverter controller parameters change)

由图11可知，随着Kppv的增大，系统的阻尼增大，Udc的振荡幅度减小，系统SSO的频率逐渐增加。同样，对比图9(a)和图11可以发现，相较于LCC-HVDC整流侧控制器参数，光伏电站逆变器外环控制参数对振荡的影响更大。

特征值根轨迹和时域仿真结果均表明，在一定参数范围内，增大Kppv能够增加系统的稳定性，提高系统SSO的阻尼，减小系统发生SSO的风险。

4.3 光伏电站直流侧电容

当光伏电站直流侧电容值C由1.0C0增加至1.4C0时，模式4的特征值根轨迹如图12所示。

图12 直流侧电容值的影响Fig. 12 Influence of capacitance value variation on DC side

随着C的增大，模式4的特征值逐渐向左移动，特征值实部减小，系统的阻尼增大，稳定性不断增强；特征值虚部减小，系统SSO频率减小。

在PSCAD/EMTDC中对上述理论分析结果进行时域仿真验证，当光伏电站直流侧电容值C为1.0C0、1.2C0、1.4C0时，直流电容电压Udc的时域仿真曲线如图13所示。

图13 直流电容电压Udc曲线(直流侧电容值变化)Fig. 13 DC capacitor voltage curve(DC side capacitance value changes)

由图13可知，随着C的增大，系统的阻尼增大，Udc的振荡幅度减小，系统SSO的频率逐渐减小。

特征值根轨迹和时域仿真结果均表明，在一定参数范围内，增大C能够增加系统的稳定性，提高系统对SSO的阻尼，减小系统发生SSO的风险。

影响因素分析表明，在光伏经LCC-HVDC外送系统中，系统主导振荡模式同时受LCC-HVDC系统和光伏电站系统参数变化的影响，表明两个子系统均参与了振荡。当LCC-HVDC整流侧控制器比例系数、光伏电站逆变器外环比例系数、直流侧电容值增大时，SSO阻尼增大；LCC-HVDC整流侧控制器积分系数增大时，SSO阻尼减小。