基于多能耦合机理的综合能源系统多元负荷协同预测模型
2022-04-08王永利周泯含姚苏航魏孟举胡梦锦
王永利, 周泯含, 姚苏航, 魏孟举, 杨 洋, 刘 钊, 胡梦锦
(1.华北电力大学 经济与管理学院, 北京 102206;2.国网河北省电力公司经济技术研究院, 河北 石家庄 050011)
0 引 言
综合能源系统可实现一定区域内不同能源的耦合互补,能够满足多元负荷需求并提高能源的利用效率。利用能源间的互补性及可替代性,综合能源系统实现了供给侧设备的耦合。电能替代政策及多元负荷之间的相互影响,又使得负荷之间存在一定的耦合关系。由于精准的负荷预测是能源系统调度优化的基础,因此,国内外众多学者在负荷预测领域有较为丰富的研究。
根据不同的负荷类别,研究重点集中于电、热、冷和气负荷的预测。关于电能的负荷预测,秦煜等[1]通过对不同耗电设备的性能分析,提出了一种基于设备工况、建筑类型以及室外气候条件的电负荷预测模型;罗澍忻等[2]综合分析考虑多种网络影响力的因素,建立了一种基于网络堆叠的长短期时间记忆网络预测模型。在热/冷负荷需求的预测方法研究中,姜平等[3]及王琦等[4]分别利用T-S模糊神经网络算法和Elman神经网络算法,建立了考虑室外温度、供回水温度、供水流量等因素的热负荷预测模型。于军琪等[5]以及邰敏等[6]提出的组合预测方法和提出的ARX模型都有效提升了冷负荷预测结果的精准度,范成等[7]运用机器学习算法对建筑冷负荷进行高精度建模,并通过构建局部线性解释模型对预测个体进行解读,同时基于局部解释模型的参数建立了一种信任指数,用于评价复杂黑箱模型的实际表现。在气负荷预测方面,刘红等[8]建立了基于回归分析的负荷预测,指导燃气的日常供应和调度。冷跻峰等[9]在处理燃气负荷的复杂性中使用EEMD自适应的时频局部化分析方法,将非线性非平稳的燃气负荷数据分解为平稳的本征模式分量及剩余项。
过去对于单个负荷的预测研究工作较为充足,但是在综合能源快速发展的背景下,国内外学者对综合能源系统多元负荷的研究工作逐步深入,涌现了大量对多元负荷预测模型的相关研究。文献[10]基于Elman神经网络及灰色神经网络方法,提出了耦合热、电负荷的预测方法;文献[11-13]和文献[14]分别考虑了气-电和热-冷负荷的相关性,构建了相应负荷预测模型。在对多元负荷进行预测的过程中,学者们采用了多种研究模型方法,例如深度学习[15]、多任务学习[16,17]、长短期记忆神经网络[18]和Copula理论[19]等方法。上述基于综合能源系统多元负荷的特性所建立的模型以及方法为后续学者的继续深入研究提供了参考价值和指导意义。
单一类型的负荷预测模型难以反映多元负荷之间的耦合关系,建立多元负荷预测模型的重要性及必要性逐渐凸显。基于此,本文综合考虑冷热电负荷的耦合特性,构建基于Copula理论的负荷相关性计算模型,并提出了一种负荷间耦合度度量方式;其次,以RBF函数作为LSSVM模型的核函数,构建LSSVM多元负荷预测模型,并利用SSA方法寻找最优参数;最后,以我国北方某一园区进行了实例验证,结果表明本文构建的模型有效提高了综合能源系统多元负荷需求的预测精确度。
1 预测模型整体结构
影响综合能源系统多元负荷的主要因素有温度、湿度等自然环境因素,也有人员流动情况、工作周期等社会环境因素。在多元负荷耦合的预测中,需要深入考虑冷热、电荷之间的耦合关系。为度量多元负荷之间的耦合关系,本文先建立了基于Copula的负荷相关分析模式,从负荷耦合度分析等角度提出多元负荷耦合关系的计算法。其中,利用樽海鞘算法解决LSSVM中正则化参数和核函数参数值的寻优问题,在预测模型中,考虑温度、湿度、工作周期等因素,并以多元负荷之间的耦合关系为影响因素,构建基于SSA-LSSVM的多元负荷预测模型,如图1所示。
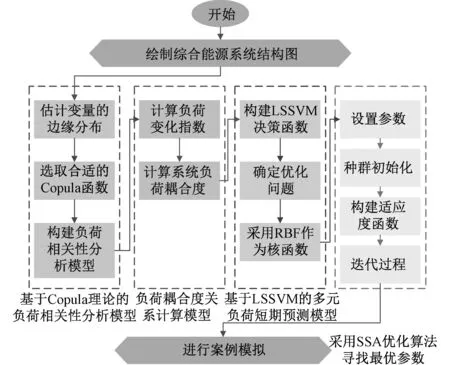
图1 模型构建流程图Fig. 1 Flow chart of model construction
2 综合能源系统多元负荷相关性分析及耦合度计算模型
综合能源系统可以同时满足对用户的负荷需要,同时实现多样化能源集成,减少消耗能源,有效地提高了能源综合利用的效率,得到了较为广泛的应用[20]。同时,在“以电代煤、以电代油、以电代气”等全球能源替代政策和科学技术支持下,冷、热、电等多种负荷之间的耦合关系逐渐加强。
准确的多元负荷预测是实现综合能源系统运行优化效果提升的重要基础,有助于正确把握综合能源系统运行优化规律。因此,本文考虑负荷之间的耦合关系并构建了综合能源系统多元负荷预测模型,基于Copula理论计算负荷相关性,衡量电、冷、热负荷之间的耦合关系,并构建耦合度计算模型,为后续负荷预测研究打下基础。
2.1 基于Copula理论的负荷相关性分析
综合能源系统多元负荷受天气等因素影响,随机性和不确定性的特征较为明显,如图2、图3所示。
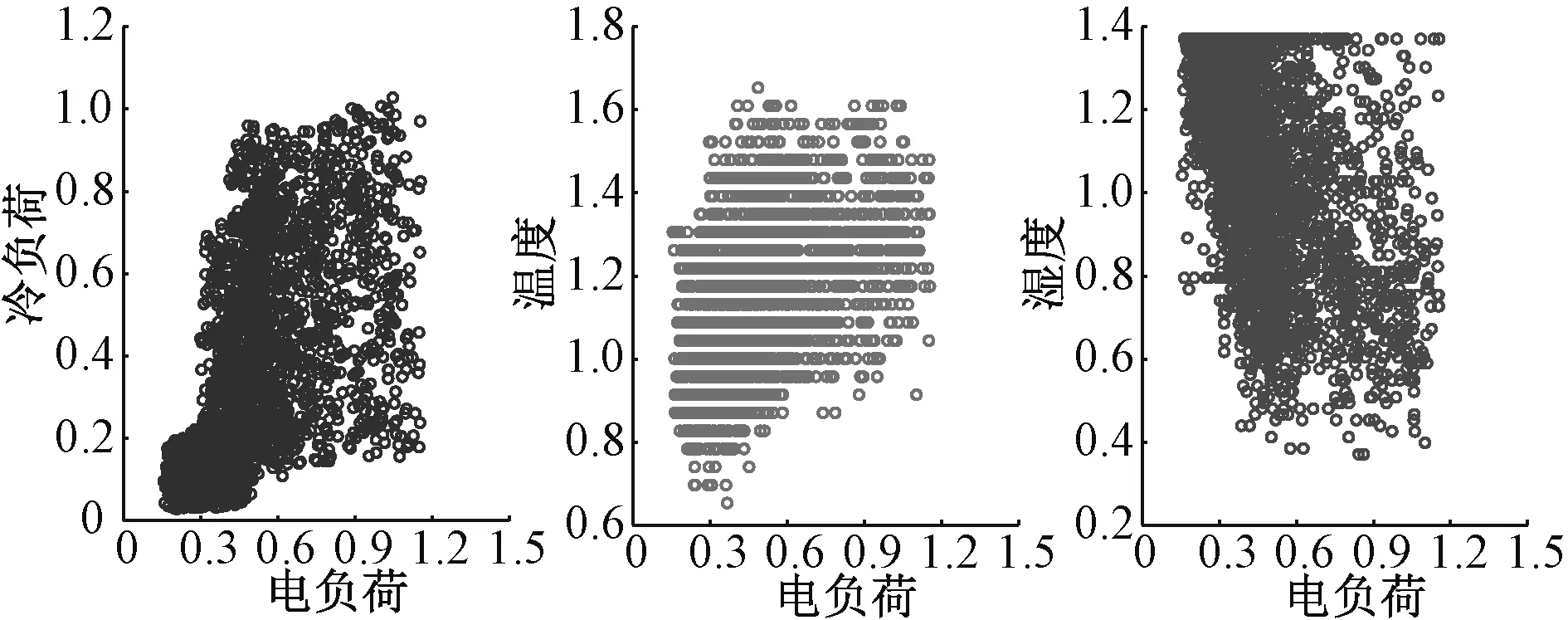
图2 供冷季电负荷与冷负荷、温度、湿度的关系Fig. 2 Relationship between electrical load and cooling load, temperature and humidity in cooling season
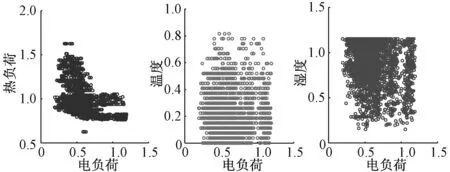
图3 供暖季电负荷与热负荷、温度、湿度的关系Fig. 3 Relationship between seasonal electrical load and heat load, temperature and humidity
由图2和图3可知,电冷热负荷之间,以及和各影响因素之间都存在较为明显的非线性关系。为了充分研究各因素间的联系,需要对多元负荷的相互关系及涉及温度湿度因素的影响进行量化分析。
Copula函数是一个用于研究变量之间的相关性的工具,它可以建立联合分布函数和其边缘分布函数之间的一定的数学联系。Copula函数定义的域是[0,1]。通过对每个随机变量边缘的分布进行估计,从而得到了分别的结果。选择合适的变量Copula并可以估算其中的参数,最后可以建立一个模型并用来帮助计算两个变量之间的相互关系。设置H为包含若干个n维随机变量的函数,F1,F2,…Fn为边缘分布函数C的边际分布,则存在Copula函数:
(1)
该函数可有效解决求解多个不确定变量联合概率分布的问题,该方法适合多元模型分布和随机模拟,可以作为对综合能源系统中多元负荷预测进行负荷相关性分析及模型研究的模型工具。
2.2 负荷耦合度关系计算模型
综合能源系统中包含了冷、热、电等各种能源负荷,通过各种能源设备,实现能源负荷之间的耦合和转换[21,22]。在冷系统中,地源热泵、常规制冷机、双工况制冷机可以将电转化为冷,热系统中的电锅炉可以将电转化为热,即冷热负荷的增加或减少可能会直接导致电负荷的变化。图4为综合能源系统典型结构。
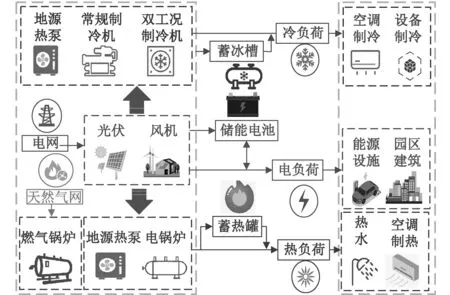
图4 综合能源系统典型结构Fig. 4 Typical structure of integrated energy system
耦合,即两个及以上的元素或系统之间存在作用并互相影响。在综合能源系统中,各负荷之间的作用定义为负荷耦合度。
基于电力容量负荷耦合计算概念和电力容量中的耦合负荷系数计算模型,本文首先建立了一个耦合度量的计算公式模型,该模型主要是用于区域性综合能源系统的负荷耦合计算。
(1)系统负荷中和变化指数计算
(a) 原始数据标准化处理:
(2)
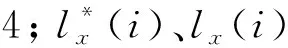
(b) 第i天电、冷、热负荷占系统负荷比重:
(3)
式中:∑l*(i)为系统第i天总负荷:
(4)
(c) 第i天系统负荷熵值e(i):
(5)
(d) 第i天系统负荷差异性系数g(i)和负荷权重ω(i):
(6)
(e) 电、冷、热负荷综合变化指数:
(7)
式中:γe、γc、γh分别为系统电、冷、热负荷综合变化指数。
(2)系统负荷耦合度计算:
(8)
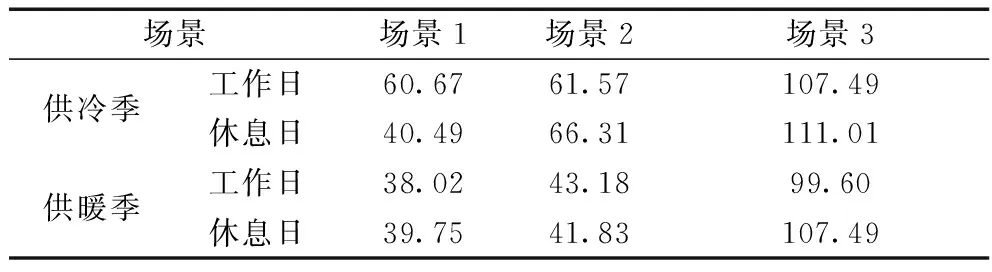
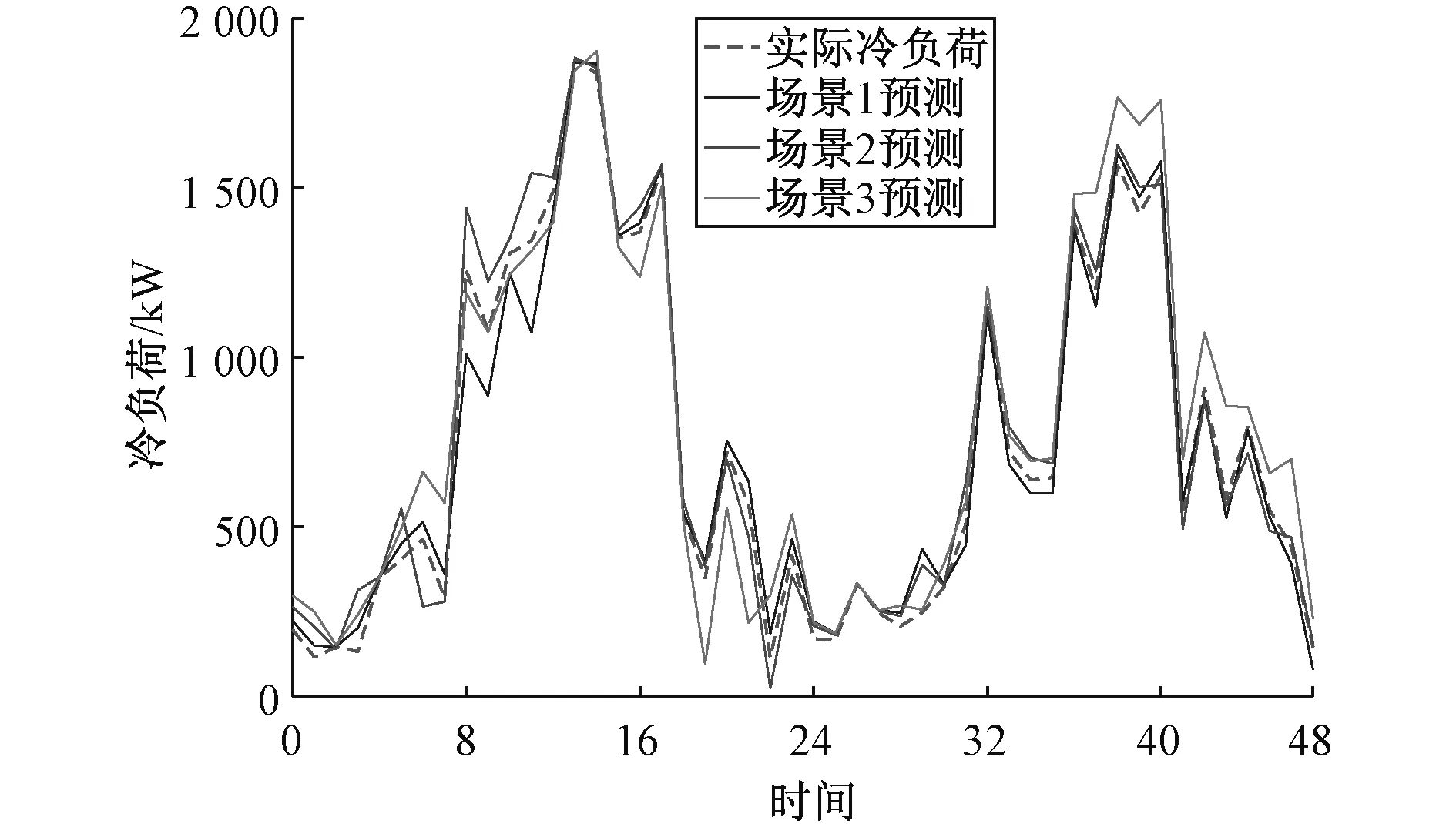
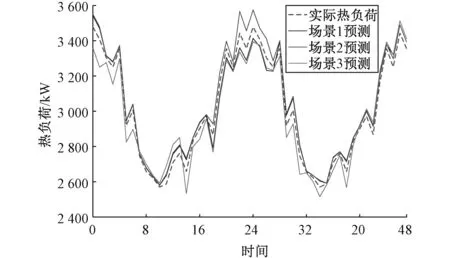
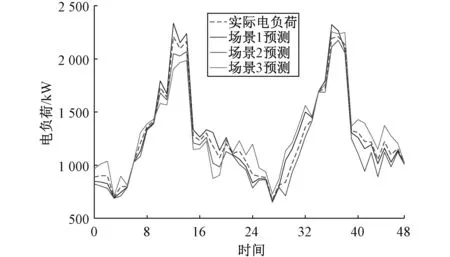
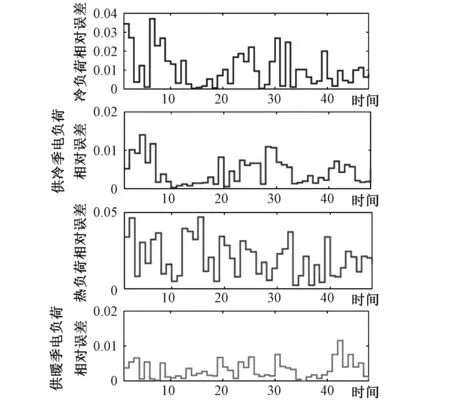
式中:Ce,c、Ce,h、Cc,h分别为电-冷,电-热,及冷-热负荷的在分析范围内耦合度值,其取值范围为[0,1]。当耦合度函数值C趋于1时,耦合度最高,表面负荷间存在较强的耦合关系;当耦合度函数值C等于0时,耦合度非常低,说明三种负荷之间并无相互作用;当0 最小二乘支持向量机(Least Squares Support Vector Machine,LSSVM)[23,24]是一种支持向量机在二次概率损失函数下的一种计算模型,可以通过求解线性模型来帮助求解优化的问题。其主要原理如下: f(x)=ωφ(x)+b (9) 式中:φ(x)为xi∈X∈Rn的非线性高维映射;ω为权值;b为偏置值。 构造结构风险函数为 (10) 式中:‖ω‖2为模型的精确性和复杂程度;c为正则化参数;Remp为经验性风险。 (11) (12) 式中:ζi为误差松弛变量,i=1,2,…,L。 则式(11)~(12)所示优化问题可表示为 (13) 式中:Iv=[1,1,…,1]T,共计l个元素,Ωij=K(xi,yj)i,j=1,2,3,…,l。 核函数本身即为映射关系的内机,在LSSVM模型中,RBF核函数的适应性表现为设置参数的数量少。因此,本文采用RBF函数为核函数,即 (14) 求解上式,直接得到决策函数: (15) 在确定正则化参数c和核函数的参数σ2的前提上,本文改进了传统LSSVM采用网络交叉验证法进行参数选择的方法,使用樽海鞘群优化算法,自动寻找最佳参数值,并减小误差。 樽海鞘是一种群体性活动的深海生物,在日常捕食等生态活动中,樽海鞘通过群体运动而形成的聚集群,称为海鞘链。澳大利亚研究学者Mirjalili S由此提出了一种关于海鞘群优化的算法(Salp Swarm Algorithm,SSA)[25]。在SSA方法中,目标群体可分为领导者和追随者两大类。领导者的角色是引导Salp群体,每个跟随者都跟随前一个。假设目标源在规划范围中存在。根据樽海鞘行为的变化,其具体优化方法如下: (1)参数设置。其主要参数分别为群体个数、影响因素的个数、最大的迭代次数、变量的上下界。 (2)初始化群体。矩阵如下: S=[sij]n×d (16) 式中:sij代表第i个樽海鞘的第j个变量值,i=1,2,…,n,j=1,2,…,d。 sij=rand(i,j)×[ub(i)-lb(i)]+lb(i) (17) 式中:rand(i,j)为设置元素定义域均为[0,1]的随机矩阵;ub(i)和lb(i)分别代表第i个樽海鞘的最大值和最小值。 (3)构建适应度函数。通过适应度函数进行计算,并设置存储数值的矩阵OS: 在矩阵OS中,目标源F即为适应度值最佳的樽海鞘,其位置由樽海鞘链影响决定,因此,求解最优数值可以通过改变目标源F位置实现。 (4)确定迭代次数。为避免出现局部最优解,需要对所有元素都进行函数运算来不断更新迭代。其中,领导者向目标源定位更新的公式为 (19) c1为 (20) 式中:L和l分别为最大和当前的迭代次数。追随者的位置更新方式如下: (21) 所有步骤都进行迭代操作直至结束。 运用SSA优化LSSVM方法构建多元负荷短期预测模型的具体流程如图5所示。 图5 基于SSA-LSSVM模型的多元负荷短期流程预测Fig. 5 Short-term multi-load process prediction based on SSA-LSSVM model 本文以北方一个园区综合能源系统的冷热电荷数据和温度、湿度等气象资料为主要仿真对象,园区综合能源系统包括电、热和冷系统,其中以电锅炉、地源热泵和电制冷机组为能量转换装置,满足了不同类型的能源需求。选择园区6月1日至9月30日的冷电负荷资料作为原始供冷季预测样本,选择7月19日为供冷期工作的典型日,7月20日为供冷期休息的典型日进行负荷预测;以12月1日次年3月18日热、电荷数据为原始供暖季预测样本,选定2月21日供暖季工作典型,2月22日供暖季休息。 为验证本文提出的SSA-LSSVM模型的负荷预测方法的效果,设置以下3种场景: 场景1:考虑负荷耦合,选用SSA- LSSVM模型; 场景2:不考虑负荷耦合,选用SSA- LSSVM模型单独预测三类负荷; 场景3:考虑负荷耦合,选用LSSVM结合的预测模型进行多元负荷预测。 其中,1~24时为工作日,25~48时为非工作日。3个场景的平均绝对误差如表1所示。 表1 各场景平均绝对误差对比Tab.1 Comparison of average absolute error of each scene 供冷季冷负荷和电负荷的预测曲线如图6和图7所示,供冷季工作日和休息日冷负荷预测的平均绝对误差分别为60.67和40.49,工作日和休息日电负荷预测的平均绝对误差分别为41.39和54.59。而场景2下,工作日和休息日冷负荷的平均绝对误差为82.94和83.16,工作日和休息日电负荷预测的平均绝对误差分别为61.57和66.31。 图6 供冷季工作日与非工作日冷负荷预测结果Fig. 6 Heat load forecast results for cooling season under working and non-working day 供暖季热负荷和电负荷的预测曲线如图8和图9所示。供暖季工作日和休息日热负荷预测的平均绝对误差分别为38.02和39.75,工作日和休息日电负荷预测的平均绝对误差分别为50.76和60.23。而场景2下,供暖季工作日和非工作日热负荷的平均绝对误差分别为43.18和41.83。这说明考虑了电负荷和热负荷之间的耦合,能提升负荷预测效果。 图8 供暖季工作日与非工作日热负荷预测结果Fig. 8 Heat load forecast results for heating season under working and non-working day 图9 供暖季工作日与非工作日电负荷预测结果Fig. 9 Electrical load forecast results for heating season under working day and non-working day 场景3下,供冷季工作日和休息日冷负荷预测的平均绝对误差分别为107.49和111.01,工作日和休息日电负荷预测的平均绝对误差分别为60.57和66.31;供暖季工作日和休息日热负荷预测的平均绝对误差分别为73.63和49.07,工作日和休息日电负荷预测的平均绝对误差分别为99.60和107.49。 由图10和表2可知,利用SSA-LSSVM模型进行负荷预测时,场景1的后验差检验均在0.19以下,小于0.35,小误差概率均在0.96以上,预测结果属于一级,总体预测精度较高。结合供冷季和供暖季冷热电负荷预测分析结果,本文构建的SSA-LSSVM模型在综合能源系统多元负荷预测模型中具有较好的预测精准度。 表2 各场景后验差检验C和小误差概率PTab.2 Posterior error test and small error probability of each scene 图10 SSA-LSSVM模型下负荷预测误差Fig. 10 SSA-LSSVM model load forecasting error 本文通过研究建立了一种基于Copula理论和SSA-LSSVM结合的综合能源系统多元负荷协同预测模型。通过Copula理论,对多元负荷之间的相互作用进行了分析,强调了各负荷之间的相互作用。其次,利用SSA算法对LSSVM的关键参数进行优化,从而有效提高了负荷预测精度。通过实例验证了预测模型的预测能力,有利于实现综合能源系统的稳定高效运行。目前本文并未考虑能源价格这一因素,未来可在此基础上进一步分析能源价格波动对多元负荷的影响。3 基于SSA-LSSVM的综合能源系统多元负荷短期预测模型
3.1 构建LSSVM预测模型
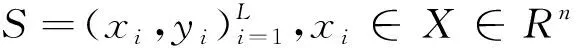
3.2 采用SSA方法寻找最优参数

4 实例分析

5 结 论
