基于正确登记概率的普查直接多报估计

吴 婷， 胡桂华

(1.重庆市万州区疾病预防控制中心， 重庆 404000；2.重庆工商大学 数学与统计学院， 重庆 400067)

0 引 言

人口普查目标是不重不漏登记普查目标总体内的每一个人，然而由于人口流动等原因，这一目标难以实现。在每次人口普查中，总是会登记普查目标总体之外的人，即普查多报人口，包括重报及其他普查多报。近几十年随着时代的变迁，重报问题变得越来越刻不容缓，其中美国、加拿大、英国、澳大利亚最近几次人口普查都十分重视重报的估计[1-4]。张广宇等[5]提到：在中国的人口普查中，户籍登记和身份证制度纳入了人口普查工作，并且将流动人口在现住地和常住地都进行登记，这样的工作可能会降低普查漏报的概率，但是却加大了重报的可能性。

2020年，我国进行了第七次全国人口普查，将对普查登记质量进行评估，多报属于人口普查质量评估的一部分，本文将深入研究普查多报。胡桂华等[6]提到普查多报又可分为重报与其他多报，在进行人口普查时，由于有些被调查者有多个住所，且对于普查的不重视或理解不到位，从而导致在多个地方进行了重复登记。对于重复登记的人，不仅要找到该人的重复登记记录，还要找到他的正确登记地址。对于普查日在多个住所活动，并进行了普查重复登记的人口，如何进行检测和解决重复登记是一大难题。

普查重报有两种统计口径，一是发生重报人数，即属于目标总体的某人不管登记了几次，只要是登记了1次以上，都看作1。该人登记了多个地址，发生重报人口数统计时，统计的是应该登记地址的发生重报人数，属于真正计数的人数且属于目标总体。二是普查重报人数，即属于目标总体的某人登记次数减1，统计的是应该登记地址的重报人数，属于重复登记的次数。而其他多报指普查员登记普查时点实际上不存在的人，例如，在普查表中登记宠物、普查时点之前死亡的人口或普查时点之后出生的人口。同一人在人口普查中登记不止一次时，被认为是重复的。重报不止发生在目标总体内，也会发生在目标总体外，但若不属于目标总体的人进行了重复登记，视为其他多报。

由文献[7]可知，目前估计多报的主要方法是利用样本普查小区多报人口及其抽样权数构造“普查直接多报估计量”。但是构造这种估计量存在两个缺陷，一是若将研究范围进行限定，在研究范围外进行了登记或多次登记，则研究范围内的多报、重报及发生重报该如何统计；二是人口流动性大，实际工作中会出现重复者应该登记位置不易确定，多报、重报及发生重报该如何统计的问题。本文目标是在有限总体概率抽样及普查多报估计理论基础上，构造基于正确登记概率的普查直接多报估计量、基于正确登记概率的普查直接重报估计量、基于正确登记概率的普查直接发生重报估计量。

基于正确登记概率的普查直接多报估计量是对于多报中的计数对象不确定哪次登记属于目标总体人口的计数而建立的，本估计量将解决上述普查直接多报估计量的两个缺陷问题。如某人在研究范围内的不同地方登记了3次，但是正确登记地址不确定，对于普查直接发生重报，是在3个地方都算作发生重报数，就将发生重报数算作了3，实际该人发生重报数为1；普查直接重报，是在3个地方都算了重报数，每个地方算的重报数都为2，总共就算作了6，实际该人重报数为2。所以，普查直接重报和普查直接发生重报分别造成了重报数和发生重报数的虚增。基于正确登记概率的普查直接多报估计量和普查直接多报估计量都属于复杂估计量，将采用分层刀切法计算其抽样方差[8-9]，将两个估计量的精度进行比较研究，为人口普查多报估计提出更符合实际的方法。

1 普查多报估计指标的构建

采取分层二重抽样进行多报研究，第一重样本采取分层整群抽样抽取，抽样单位为普查小区。用H表示第一重样本抽样层的总层数，h为任意层，Nh为层h的普查小区总数，nh为层h抽取的样本普查小区总数；g为第二重抽样层，αhg为样本普查小区集合，Mhg为层hg普查小区总数，mhg为层hg样本普查小区总数。

进行分层二重抽样后得到样本小区i，将样本小区i的人口普查名单和事后质量抽查名单进行数据处理和数据比对后得到表1中的指标，为构造正确登记概率的普查直接多报估计量提供基础。

表1 层hg第i样本小区登记人口数的分类

根据表1，将普查登记人口数分为三大类，计数对象属于目标总体人口的计数确定、计数对象不属于目标总体人口的计数确定和计数对象不确定哪次登记属于目标总体人口的计数。

将计数对象属于目标总体人口的计数确定进行分类得到发生重报人数c1hgi和不发生重报人数c0hgi，这两部分是属于目标总体样本小区的确定人口数。发生重报的人口数c1hgi，指在本小区进行了一次登记且在本小区外研究范围内的其他地方进行了登记，但是正确登记地址属于本小区的人数。不发生重报人口数c0hgi，指被计数者在本小区登记一次且未在研究范围内其他地方进行登记，正确登记地址在本小区的人数。

将计数对象不属于目标总体人口的计数确定进行分类得到重报人数d1hgi和其他多报人数d0hgi，这两部分是不属于目标总体样本小区的确定人口数。重报人数d1hgi，指在本小区进行了一次登记且在本小区外研究范围内的其他地方进行了登记，但是正确登记地址不属于本小区的人数。其他多报人数d0hgi，指普查员将研究范围内普查时点前死亡的人口、普查时点后出生的人口或宠物进行了登记。

计数对象不确定哪次登记属于目标总体人口的计数，根据重报的两种统计口径分为发生重报概率人数pc1hgi和重报概率人数pc2hgi。发生重报概率人数pc1hgi，指在本小区进行了一次登记且在本小区外研究范围内的其他地方也进行了登记，但是正确登记地址不确定是否属于本小区的人数，将根据式(1)进行概率登记，统计的是发生重报的概率。发生重报概率人数pc2hgi，指在本小区进行了一次登记且在本小区外研究范围内的其他地方也进行了登记，但是正确登记地址不确定是否属于本小区的人数，将根据式(2)进行概率登记，统计的是重报的概率。

对于登记地址不确定者，如某人进行了多次普查登记，但不确定哪一次登记才算做应该登记，若在每个地方都算作重报或发生重报，将虚增多报人口数。对于这种情况，将在每个地址都进行概率登记处理。

重报者A每个登记地址发生重报应该登记的概率为PA,Duplicate1，Duplicate1表示发生重报，对于重报者A，n表示对于重报者A普查登记次数，发生重报概率：

PA,Duplicate1=1/n(n>1)

(1)

重报者A每个登记地址重报概率为PA,Duplicate2，Duplicate2表示重报，对于重报者A，n表示对于重报者普查登记次数，重报概率：

PA,Duplicate2=(n-1)/n(n>1)

(2)

(3)

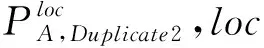
(4)

其中，D表示Duplicate2。

2 普查多报估计量的构造

2.1 普查直接多报估计量的构造

在普查直接多报估计中，表1的计数对象不确定哪次登记属于目标总体人口的计数时，根据重报的两种统计口径，分为直接发生重报e1hgi和直接重报e2hgi。根据表1建立的相关指标得到普查直接发生重报估计量、普查直接重报估计量、普查直接其他多报估计量和普查直接多报估计量。

二重抽样后，用bhgi表示示性函数，如果第一重样本普查小区i属于层g，则bhgi=1，否则bhgi=0。用Ihgi表示另外一个示性函数，如果第一重样本普查小区i进入αhg，则Ihgi=1，否则Ihgi=0。样本小区i的抽样权数αhgi为(Nh/nh)(Mhg/mhg)。

(5)

式(5)是构造的普查直接发生重报估计量，是重报的口径之一，统计人口普查中有多少人口发生了重复登记。

(6)

式(6)是构造的普查直接重报估计量，体现哪些重复登记导致实际普查人口数的增加，每一个重复登记者重复登记的次数不一致，并且重复登记的原因是不同的，该估计量可以获得因为重复登记导致的实际人口虚增的人口数。

(7)

式(7)构造的是普查直接其他多报估计量，目的是估计总体中的其他多报人口数，该估计量也导致实际人口数的增加，但不是由于重复登记导致的增加，而是登记了不属于普查时点的人口数，如宠物、普查时点前死亡的人口、普查时点后出生的人口。有些国家觉得其他多报人口数少，于是没有估计或者单独估计。但其他多报属于多报的一部分，在多报估计工作中也不应忽视它的存在。

(8)

式(8)是式(6)和式(7)的总和，代表的是总体中人口普查重报与其他多报的人口数，该指标能获知普查人口相对于实际人口虚增的人口数。

2.2 基于正确登记概率的普查直接多报估计量的构造

(9)

式(9)构造的是基于正确登记概率的普查直接发生重报估计量，该估计量相对于式(5)构造的普查直接发生重报估计量，对计数对象不确定哪次登记属于目标总体的人口，进行发生重报概率登记，以免造成发生重报的估计增多。

(10)

式(10)构造的是基于正确登记概率的普查直接重报估计量，该估计量相对于式(6)构造的普查直接重报估计量，对计数对象不确定哪次登记属于目标总体的人口，进行重报概率登记，以免造成重报的估计增多。

(11)

式(11)构造的是基于正确登记概率的普查直接多报估计量，该估计量相对于式(8)构造的普查直接多报估计量，对重复计数对象不确定哪次登记属于目标总体的人口，进行重报概率登记，以免造成多报的估计增多。

3 普查多报估计量的方差估计

在构造式(5)——式(11)之后，所要做的工作是计算它们的抽样方差。下面将对普查直接多报估计量及其相关估计量和基于正确登记概率的普查直接多报估计量及其相关估计量的抽样方差估计量进行构造。

(12)

3.1 普查直接多报估计量的方差估计

(13)

(14)

(15)

(16)

(17)

(18)

e2hgi+d0hgi)

(19)

(20)

3.2 基于正确登记概率的普查直接多报估计量的方差估计

(21)

(22)

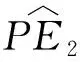
(23)

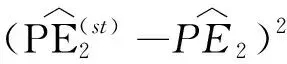
(24)

(25)

(26)

4 实证分析

4.1 样本数据

本文的实证数据主要来源于调查数据，其调查的实证对象是广西南宁市西乡塘区的某行政区，采取了分层二重抽样方法，所抽取的样本见表2。

在表2中，该行政区分为两层：社区层和行政村层，分别用h=1和h=2表示。社区层共有普查小区1 000个，行政村层共有普查小区1 100个。从社区层和行政村层分别简单随机抽取10个和9个普查小区。按照调查难度，将第一重样本普查小区分为3层，即容易调查层、中等难度调查层和调查难度大层，分别用符号g=1，g=2和g=3表示。所有样本普查小区及其个人100%提供答复，此时样本个人抽样权数等于样本普查小区抽样权数。抽样层、抽样权数及样本数据见表2和表3。其中，Nh和nh分别表示层h的普查小区总数及样本普查小区数，Mhg和mhg分别表示层hg的普查小区数及从中抽取的第二重样本普查小区数，i表示样本普查小区，表3中的(2)表示第一重样本普查小区进入到第二重样本。

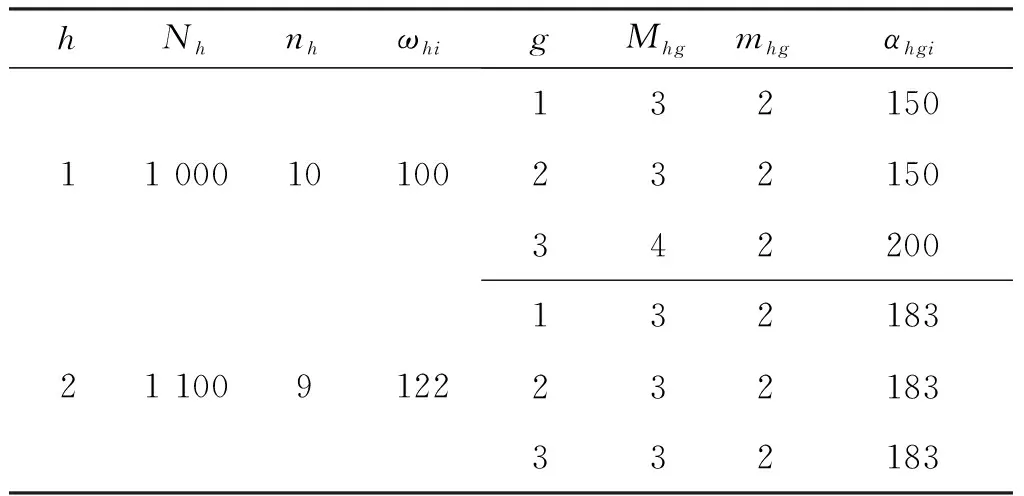
表2 二重抽样样本分布情况表Table 2 Distribution of double sampling samples

在抽取的样本小区中，只有样本小区1、样本小区5、样本小区14、样本小区17有人存在重复登记的计数对象不确定是否属于目标总体，他们属于在普查研究范围内的登记次数超过1，并且不确定哪次登记属于目标总体人口。根据上文中指标解释，基于式(3)和式(4)，得出普查直接多报估计量和基于正确登记概率的普查直接多报估计量所需要的样本数据资料(表4)。

4.2 基于正确登记概率的普查直接多报估计值

表的抽样方差计算Table 5 Sampling variance calculation of

从表5的数据可以看出：总体普查发生重报人口数1 898人的抽样方差为783 821，抽样标准差为885人。这表明，平均每个样本估计的总体普查发生重报人口数为1 898人，相应的抽样平均标准误差为885人，即每个样本估计总体普查发生重报人口数与总体实际普查发生重报人口数的平均差异为885人。

4.3 两个多报及多报率估计量的比较

现在进行这两个多报估计量数据精度上的比较。在这之前，把普查直接多报估计值和基于正确登记概率的普查直接多报估计值及其抽样方差估计值统一列在表6中。

表6 普查多报估计值Table 6 Estimates of overcoverage in census

从表6可以得出：普查直接发生重报估计量估计的发生重报人口数为1 898人，抽样标准误差为885人，而基于正确登记概率的普查直接发生重报估计量估计的发生重报人口数为1 227人，抽样标准误差为579人,普查直接发生重报估计值及抽样标准误差都高于基于正确登记概率的普查直接发生重报估计值及抽样标准误差，普查直接发生重报人数虚增了发生重报人口数；普查直接重报估计量估计的重报人口数为3 563人，抽样标准误差为1 364人，而基于正确登记概率的普查直接重报估计量估计的重报人口数为1 388人，抽样标准误差为348人，普查直接重报估计值及抽样标准误差都高于基于正确登记概率的普查直接重报估计值及抽样标准误差，前者虚增了重报人口数；普查直接其他多报估计量估计的其他多报人数为533人，抽样标准误差为345人，普查直接其他多报人数估计的是在普查中将普查时点前死亡人口、普查时点后出生人口或宠物登记的数目，且包含这些登记的重复登记数目；普查直接多报估计量估计的多报总人口数为4 096人，抽样标准误差为1 292人，而基于正确登记概率的普查直接多报估计量提供的多报人口总数为1 921人，抽样标准误差为350人，它们都是各自统计的重报人口与其他多报人口之和，普查直接多报估计值及抽样标准误差都高于基于正确登记概率的普查直接多报估计值及抽样标准误差，普查直接多报人数虚增了多报人口数。

5 结 论

本文以广西南宁市西乡塘区的一个行政区为观测对象，从现有的国际多报研究基础上，通过对多报、重报及其他多报定义的明确，构造直接普查多报估计量的模型，并构造直接其他多报估计量，及从重报的两种口径构造的重报估计量。本文新建的另一种多报模型是构造基于正确登记概率的普查直接多报估计量，并从重报的两种口径构造基于正确登记概率的重报估计量及发生重报估计量。本文对两种普查多报模型进行理论和实证研究后，最终得出如下结论：

为了比较普查直接多报估计量和基于正确登记概率的普查直接多报估计量的估计精度，并且为了使得这种比较具有可比性，统一使用刀切法近似计算其抽样方差。