基于LSTM-HFTS-EC的PM2.5区间多尺度组合预测研究

罗 瑞， 刘金培， 陈华友， 陶志富

(1. 安徽大学 商学院，合肥 230601； 2. 安徽大学 数学科学学院，合肥 230601)

0 引 言

PM2.5指大气中空气动力学当量直径小于等于2.5 μm的颗粒物，它长时间悬浮于空气中，会侵蚀人体免疫力，引发心血管和呼吸道等疾病[1]。PM2.5的浓度值是连续变化的，每日最低值和最高值差异大，具有一定的时间跨度和区间关联度。因此，PM2.5的日均值时间序列无法有效反映其浓度值的真实变化，而以PM2.5日最高和最低浓度值分别作为上下限的区间型数据则包含了更多的真实信息，不但可以有效反映其日变化趋势和范围，并且具有更高的稳定性和更强的泛化能力[2]。因此，PM2.5区间时间序列预测具有更重要的理论和现实意义。

PM2.5浓度值预测方法主要分为3类：数值模拟法[3]、统计预测法[4-6]和深度学习方法[7-10]。数值模拟法在气象学原理的基础上，通过数学方程模拟PM2.5的扩散、转化以及消散的过程[2]。此类模型中的参数存在一定的不确定性，导致其预测结果也会存在一定的偏差。统计预测法则是通过回归或机器学习等建立PM2.5与影响因素之间的关系[4]，实现对PM2.5的预测，主要包括多元线性回归(MLR)[5]、支持向量机(SVM)[6]、人工神经网络(ANN)[4]等预测方法。统计类方法虽然能够对PM2.5的变化规律以及相关影响因素之间的潜在关系进行拟合，但需要从大量的样本数据中提取时间序列特征，对于波动程度较大的时间序列，存在拟合效果不稳定的缺点。

深度学习方法通过学习时间序列数据的内在规律和表现层次，能更好地拟合时间序列，提高预测精度[7-10]，主要包括循环神经网络(RNN)、卷积神经网络(CNN)和长短期记忆模型(LSTM)等方法。其中，CNN的优势在于可以学习和有效提取数据的空间特征；RNN则存在梯度消失的问题，不适用于长期时间序列的预测；LSTM是对RNN的改进，它解决了RNN存在的问题，能够有效提取数据的时间尺度特征。因此，与RNN和CNN相比，LSTM更适用于时间序列的预测[7]。Ong等[8]提出基于RNN的深度学习预测框架，对城市的PM2.5浓度值进行预测。Wu等[9]提出了基于LSTM的PM2.5预测方法，对武汉市PM2.5浓度值进行预测。曲悦等[10]分别利用BP神经网络、CNN与LSTM对PM2.5等空气污染物进行预测。上述基于深度学习的预测模型均能较好提取单一尺度的数据特征，相对于数值模拟法和统计预测法具有更好的预测效果。但是，对于多尺度的复杂时间序列，存在有效信息提取不完全问题。最新研究表明，针对非线性、非平稳性、波动性强的时间序列，先对其进行多尺度分解，使得各子序列具有更好的波动规律性，再对分解后的各层序列分别进行预测分析，可有效提高预测精度[11-12]。为了简化复杂数据，使各子序列平稳化和规律化，从而有效减少预测误差，本文将深度学习与多尺度分解相结合，先选取区间分解方法将PM2.5区间序列分解为不同波动频率的子序列，进而采用深度学习方法对高频波动的子序列进行预测。

综上所述，现有研究存在以下3个方面的问题：已有研究主要关注PM2.5的日均点值时间序列预测，而针对PM2.5区间预测的研究较少；如何结合深度学习模型，建立复杂区间时间序列的多尺度分解预测新方法，仍然需要进一步探讨；已有区间时间序列预测方法大多仅关注提高原始序列的预测性能，而没有充分利用预测误差序列中隐含的有效信息。

针对以上问题，提出一种新的基于LSTM-HFTS-EC的PM2.5区间多尺度组合预测新方法。首先，提出区间时间序列经验模态分解(IEMD)方法，将PM2.5区间时间序列依次分解为区间趋势序列、低频波动序列和高频波动序列；然后，分别利用Holt-Winters模型、混合模糊时间序列模型(HFTS)和LSTM模型对区间趋势序列、低频波动序列和高频波动序列进行预测，并将预测结果集成为PM2.5的区间预测值；为了进一步提高区间预测的精确度，再利用LSTM模型对PM2.5区间预测值进行误差修正，即得到PM2.5的最终区间预测结果。最后，将本文的预测方法进行实证预测分析，通过对比来检验本文所提出的组合预测方法的准确性和适用性。

1 PM2.5区间时间序列

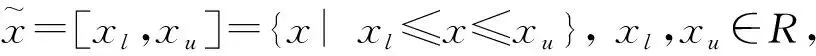
PM2.5浓度值的日度区间数如图1所示，区间下界为每日PM2.5的最低浓度值，区间上界为每日PM2.5能达到的最高浓度值，区间半径则代表了PM2.5浓度值的日变化范围。

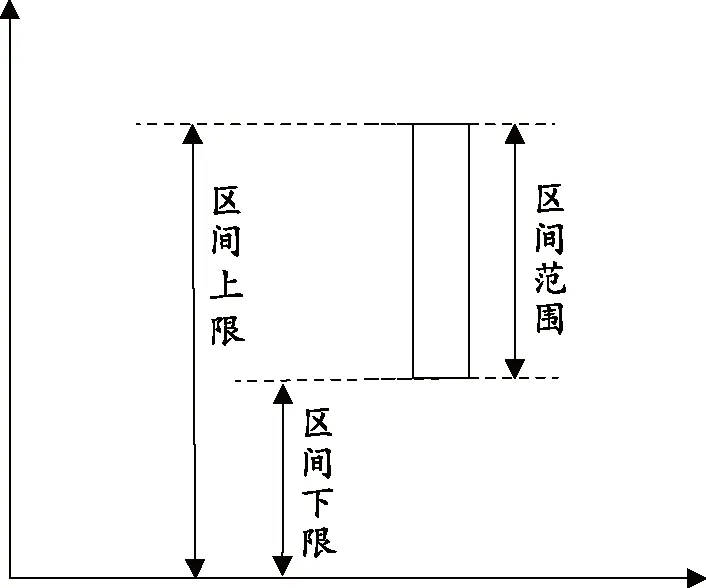
图1 PM2.5浓度值日度区间数

以合肥市为例，合肥市2018-07-08至2018-07-16共9 d的PM2.5浓度的区间序列如图2所示，可见PM2.5浓度值处于连续变化中，日度区间序列的上下界差异大，具有较大的变化范围和较强的波动性。可见，传统的PM2.5日均值时间序列预测的代表性弱，无法充分反映其波动规律。

图2 合肥市PM2.5日度区间序列

2 方法与原理

2.1 IEMD

在经验模态分解的基础上，提出IEMD方法。具体步骤如下：

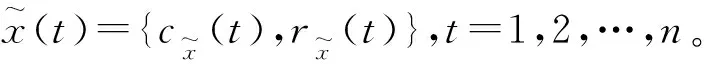
步骤2 分别计算中心和半径时序上下包络线的均值mc(t)和mr(t)，其中mc(t)=(ecmax(t)+ecmin(t))/2，mr(t)=(ermax(t)+ermin(t))/2。再分别计算中心和半径时序与其平均值之间的差值，记为dc(t)和dr(t)，这里dc(t)=c(t)-mc(t)，dr(t)=r(t)-mr(t)。

步骤3 分别判断序列dc(t)和dr(t)是否满足本征模态函数(IMF)的条件[13]。若满足，则记为1个IMF，记fcm(t)=dc(t)，frn(t)=dr(t),m=1,2,…,M,n=1,2,…,N。将剩余项rc(t)=c(t)-fcm(t)和rr(t)=r(t)-frn(t)分别作为新的c(t)和r(t)。若不满足，则记c(t)=dc(t)，r(t)=dr(t)重复步骤1～步骤2的过程。

步骤4 重复步骤1～步骤3，直到无法再从c(t)和r(t)中分解出新的IMF为止。此时，则c(t)和r(t)分别分解为多个IMF和一个趋势项，即

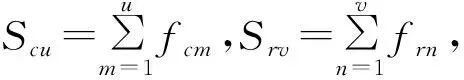
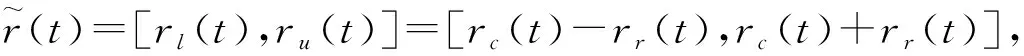
本文提出的IEMD分解方法能够将区间时间序列分解为区间趋势序列、低频波动序列和高频波动序列，它不仅能够充分提取区间时间序列中所包含的不同尺度的特征信息，而且避免了序列的过度分解，可以进一步简化预测过程的复杂性。

2.2 单项预测方法

2.2.1 LSTM

LSTM为RNN的一种改进，成功解决了RNN存在的梯度爆炸和梯度消失问题[14]。通过设置门限控制信息的取舍，解决了长期依赖问题，实现了神经网络的遗忘和记忆功能。LSTM有3个门限，分别为遗忘门(Forget Gate)、输入门(Input Gate)和输出门(Output Gate)。LSTM的算法结构如图3所示。

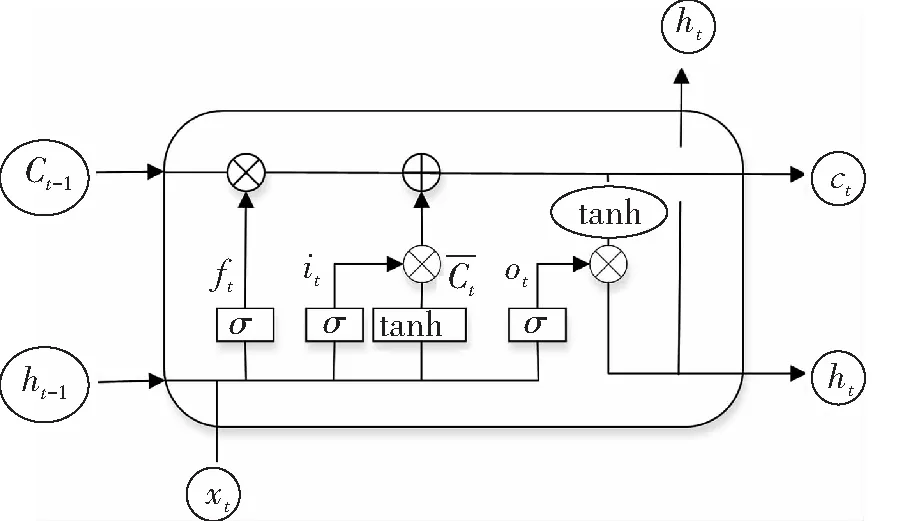
图3 长短期记忆神经网络的算法结构图

在图3中，方框内上方的水平线即为单元状态，控制信息传递给下一时刻。LSTM的前馈计算过程分为3步。

第一步决定历史信息是否可以通过单元状态，即遗忘掉不重要的历史信息，这一步由遗忘门来控制，上一时刻的输出信息ht-1和当前时刻的输入信息xt经过sigmoid激活函数σ得到函数值ft∈[0,1]，决定历史信息Ct-1通过单元状态的程度。

ft=σ(Wf·[ht-1,xt]+bf)

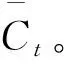
it=σ(Wi·[ht-1,xt]+bi)

(1)

(2)

(3)

第三步决定单元状态中有多少信息需要在当前时刻输出，这一步由输出门决定。根据式(4)得到输出门的值ot，由式(5)计算LSTM当前时刻的输出值ht。其中，W、b分别表示各“门限”的权重矩阵和偏置向量。

ot=σ(Wo·[ht-1,xt]+bo)

(4)

ht=ot*tanh(Ct)

(5)

2.2.2 HFTS预测

HFTS预测模型是传统模糊时间序列(FTS)预测[16]的改进。模糊集、模糊时间序列和模糊关系的定义如下：

定义2[17]令U为给定论域，将论域划分为n个子区间，则U={u1,u2,…,un}，定义A为论域U上的模糊集，并记A=fA(u1)/u1+fA(u2)/u2+…+fA(un)/un。其中，fA(·)是定义在模糊集A上的隶属函数，fA(·):U→[0,1]；fA(ui)表示ui在模糊集A上的隶属度，i=1,2,…,n。

定义3[17]令R中一子集Y(t)，(t=1,2,…)为给定论域，fi(t)为定义在其上的模糊集(i=1,2,…)，且F(t)={f1(t),f2(t),…}，则称F(t)为定义在Y(t)上的模糊时间序列。

定义4[17]假设F(t)由F(t-1)所引起，即F(t-1)→F(t)，此关系可表示为F(t)=F(t-1)∘R(t,t-1)，则称F(t)为一阶模糊，R(t,t-1)为F(t-1)与F(t)之间的模糊关系。其中，符号“∘”表示合成运算。

HFTS预测方法的算法步骤如下：

步骤1 利用模糊C均值聚类(FCM)[20]将论域U划分为n个区间，并且确定训练数据属于各区间的隶属度。

步骤2 结合训练数据属于各模糊集的隶属度，将时间序列转化为FTS。

步骤3 利用BP神经网络定义模糊关系，将前m期数据属于各模糊集的隶属度作为BP神经网络的输入值，将后一期数据的实际值作为BP神经网络的输出值。

步骤4 确定BP神经网络隐含层的神经元个数、激活函数以及相关参数，构建网络结构。

步骤5 利用训练集数据对网络进行训练。

步骤6 利用训练好的网络进行预测。

HFTS能有效地解决FTS存在的3个问题：在模糊化阶段，HFTS利用系统的FCM方法将数据集模糊化，以此得到各数据更加客观的隶属度，从而解决了FTS中隶属度存在极大主观性的问题；同时，在建立模糊关系阶段，HFTS通过BP神经网络消除了模糊关系的结构性选择问题，并且避免了复杂的模糊关系矩阵计算[18]；另外，HFTS通过将时间序列的实际值作为目标值，利用BP神经网络进行预测，避免了去模糊化阶段中可能出现的预测误差，从而提高了预测性能。

2.2.3 Holt-Winters模型

Holt-Winters模型适用于对含有趋势变动、季节变动和周期变动的时间序列进行预测。本文应用的乘法Holt-Winters预测模型[19]，如下：

(6)

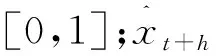
3 预测模型

针对PM2.5区间时间序列数据非线性、非平稳性和波动幅度较大等特点，提出一种新的基于LSTM-HFTS-EC的PM2.5区间多尺度组合预测方法，结构框架如图4所示，具体步骤如下：

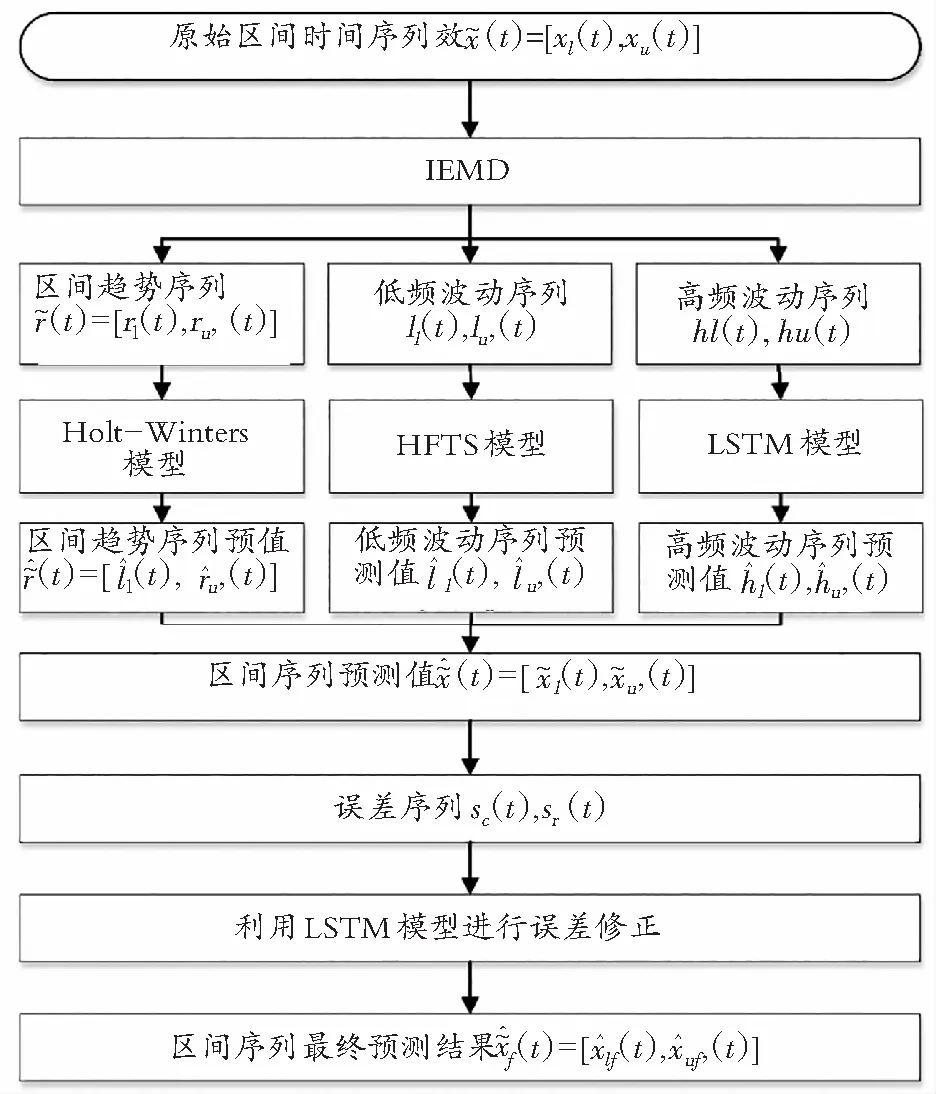
图4 组合预测模型结构框架

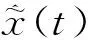
步骤5 模型检验。利用区间平均相对误差(IARV)、区间平均绝对误差(IMAE)、区间平均绝对百分比误差(IMAPE)和区间均方根误差(IRMSE)4种预测误差评价指标对本模型以及其他预测模型进行对比分析，以此检验本文提出模型的预测效果。

4 实证研究

4.1 数据来源和预处理

选取合肥市2018-07-01至2020-12-30共计914 d的PM2.5数据进行预测实证分析，数据来源于安徽省生态环境厅(http://sthjt.ah.gov.cn)。对收集的PM2.5实时数据进行预处理，将日实时数据的最高值和最低值分别作为区间的上下限，得到PM2.5区间时间序列。其中，选取前822个区间数据作为训练集，后92个区间数据作为测试集。

4.2 区间数据的多尺度分解

根据提出的组合预测模型流程，利用IEMD方法将合肥市PM2.5原始区间时间序列依次分解为区间趋势序列、低频波动序列和高频波动序列，结果如图5所示。其中，IEMD是一种自适应分解方法，勿需提前设置分解函数和分解层数，该方法可以自行分解成对应的层数。图5(a)为分解得到的区间趋势序列，它体现了合肥市PM2.5浓度值的整体趋势，可见受新冠疫情等因素影响，合肥市PM2.5浓度值在一段时期内处于下降趋势，而随着工业生产的全面复工以及出行的常态化，其浓度值也逐渐上升。图5(b)为低频波动序列，反映了合肥市PM2.5浓度值的短期变化规律，从图5中可以看出其浓度值具有明显的季节性和周期性，说明冬季合肥市PM2.5浓度值会达到最高峰，空气污染比较严重，在夏季合肥市PM2.5浓度值会处于最低水平，空气质量相对较好。图5(c)表示高频波动序列，它体现了在众多因素影响下合肥市PM2.5浓度值的具体波动细节，可以发现合肥市PM2.5浓度值的波动幅度较大。

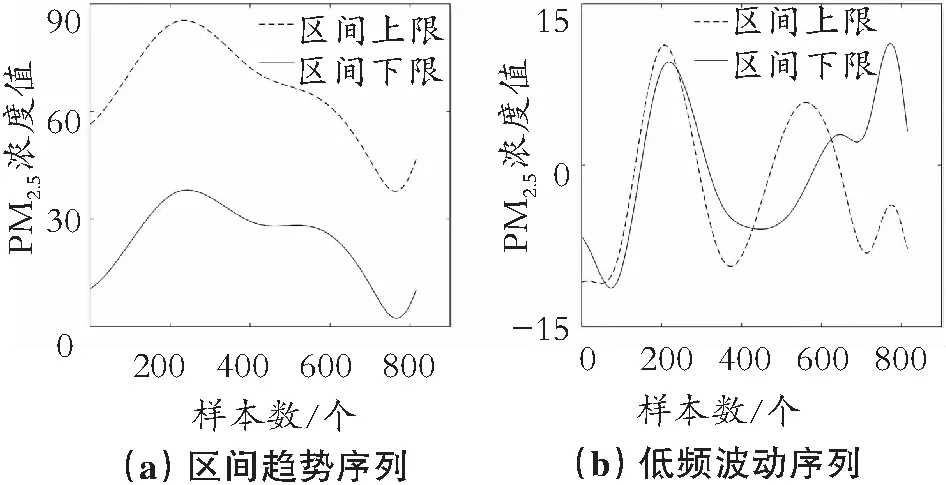
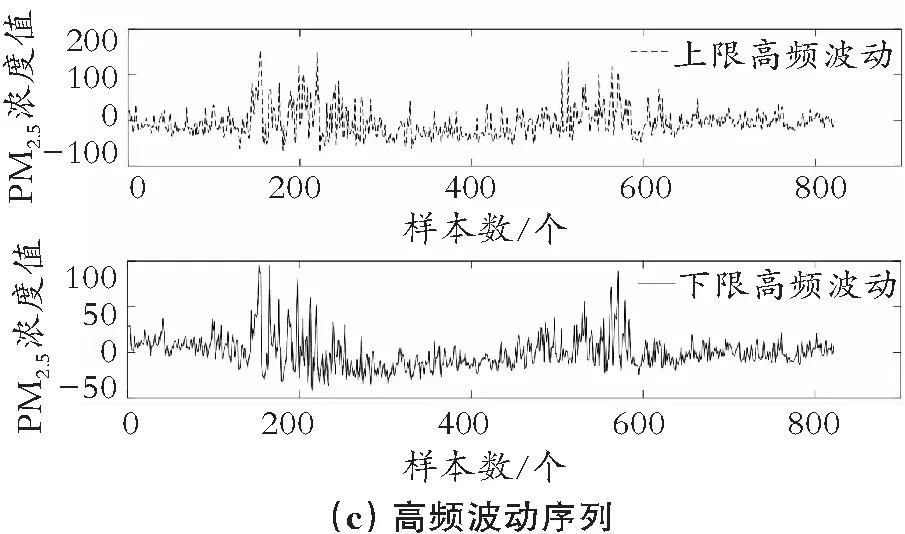
图5 PM2.5原始区间数据分解图

4.3 组合预测

在上一阶段的基础上，首先采用Holt-Winters对区间趋势序列进行预测，平滑系数分别设置为α=0.3、β=0.3和γ=0.4。然后基于HFTS对低频波动序列进行预测，其中，FCM的类别数n=5，BP神经网络的输入值m=5，隐含层的神经元个数设置为16，激活函数为tansig，迭代次数为1 000。最后选取LSTM对高频波动序列进行单步预测，其中，本文设置1个输入层、1个隐含层和1个输出层，隐含层的神经元个数为128，激活函数设置为tanh，时间步长设置为1，批处理大小取值为50，迭代次数设置为500。同时，将各单项预测方法的预测结果进行相加集成，得到合肥市PM2.5组合预测值如图6所示。可以看出，虽然组合预测值整体可以反映PM2.5实际值的变化趋势，但是PM2.5区间浓度值上限和下限的预测结果与实际值之间在波动细节上仍存在一定的差异。

说明高频波动序列中隐含的一部分复杂数据特征没有被有效利用，因此，预测结果仍然有改进的空间。

4.4 误差修正

基于组合预测的结果，进一步采用误差修正的方法，从预测误差中间接提取隐含的有效信息，进一步提高预测精度。首先，计算得到原始数据与PM2.5组合预测结果之间的差值作为误差序列。然后，采用LSTM对误差序列进行预测，在相关参数设置不改变的情况下，将前一期数据作为输入值，后一期数据作为输出值，得到误差序列的预测结果。最后，利用误差预测值对组合预测的结果进行修正，将两者相加集成，得到PM2.5区间浓度值最终预测结果，如图6所示。由此可见，进行误差修正后的预测结果更加接近于实际值，预测效果得到了较大地提升。说明误差修正能够从预测误差序列中进一步提取有效信息，提高模型的预测精度。

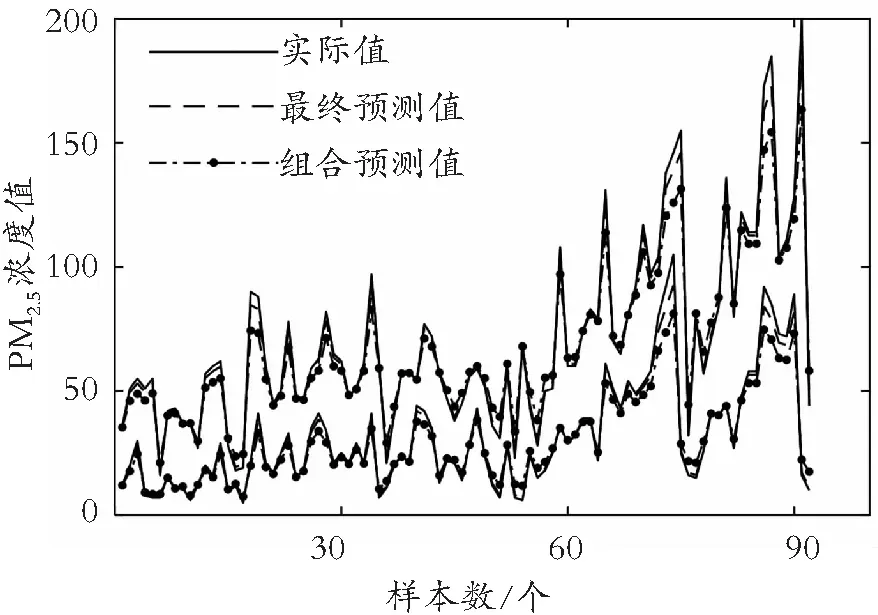
图6 预测结果对比图

4.5 多种方法预测效果对比分析

为了验证所提出模型的有效性，进行了以下3个方面的对比，并用散点图表示。各数据点越趋于对角线表明预测结果越接近实际值，反之，效果越差。对比分析结果如下：

(1) 不同分解方法的对比。在本文方法的基础上，对分解方法进行变换，采用变分模态分解(VMD)、集成经验模态分解(EEMD)、奇异谱分解(SSA)对PM2.5原始区间数据进行分解处理，并将其记为VMD-CF-ECM、EEMD-CF-ECM和SSA-CF-ECM。对比结果如图7所示(❋、☆、▽、×分别代表IEMD-CF-ECM、VMD-CF-ECM、EEMD-CF-ECM、SSA-CF-ECM)，本文模型(IEMD-CF-ECM)的预测效果明显优于这3种模型，由此可见IEMD非常适用于分析波动幅度不规律、非线性和非平稳性的区间时间序列，它能根据数据固有的波动尺度特征来进行时间序列分解，具有客观性和自适应性。

(a) 下限预测效果对比

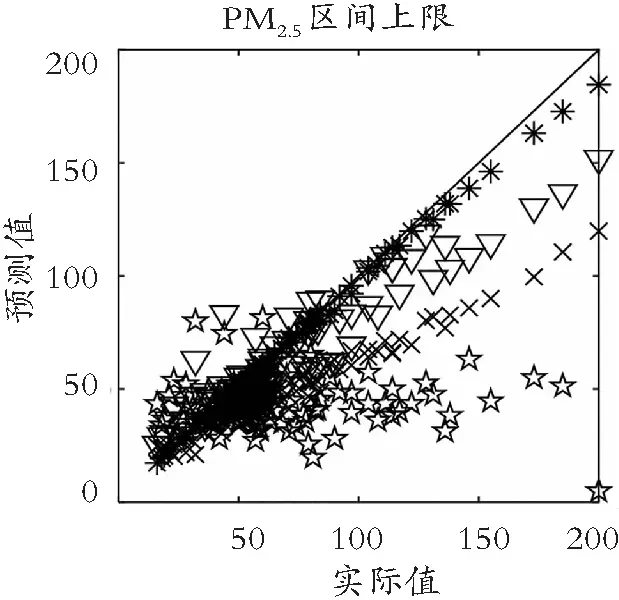
(b) 上限预测效果对比图7 本模型与采用不同的分解方法比较图

(2) 不同单项预测方法的对比。在本模型基础上，对分解后的不同频率序列分别采用同一单项方法进行预测,如LSTM、HFTS和Holt-Winters，并依次将其设定为IEMD-LSTM-ECM、IEMD-HFTS-ECM和IEMD-HW-ECM。由图8可知(❋、□、+、▽分别代表IEMD-CF-ECM、IEMD-LSTM-ECM、IEMD-HFTS-ECM、IEMD-HW-ECM)，采用单项预测方法的预测精度低于本文提出的组合预测方法，这说明利用IEMD将PM2.5区间序列分解为不同尺度的子序列，然后根据不同时序的数据特征，选择最合适的模型，利用组合预测方法对其进行预测，能够极大程度地提高预测性能，从而达到最优预测效果。

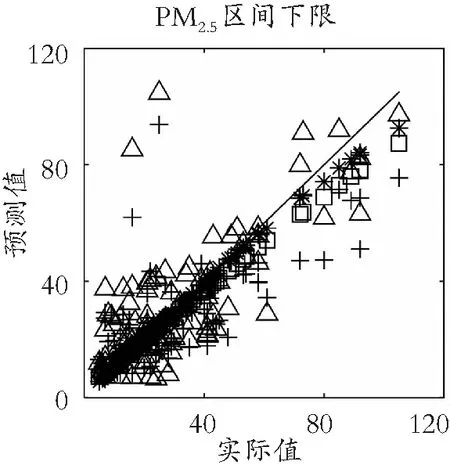
(a) 下限预测效果对比

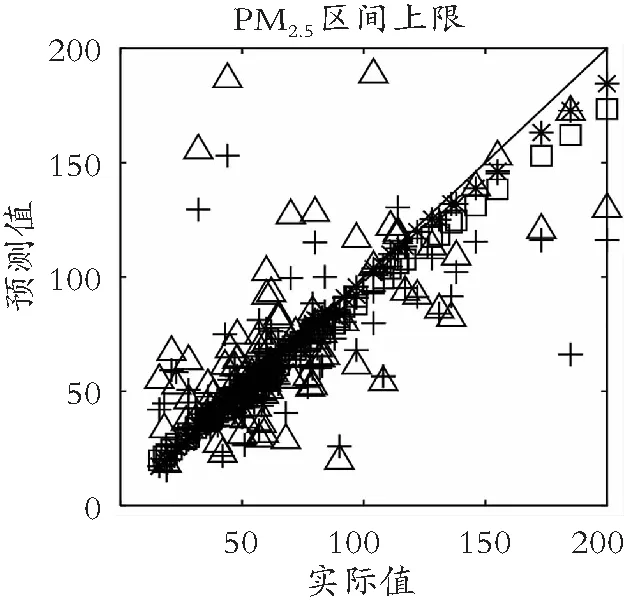
(b) 上限预测效果对比图8 本模型与采用单一预测方法比较图

(3) 与已有预测模型的横向对比。将本文模型与其他PM2.5预测模型进行对比，如LSTM模型[10]、ANN模型[21]和Holt-Winters模型[21]。对比结果如图9所示(❋、○、☆、×分别代表IEMD-CF-ECM、LSTM、ANN、HW)，可见对比模型的预测效果远低于本文提出模型，由此可见，本模型具有更高的预测精度。

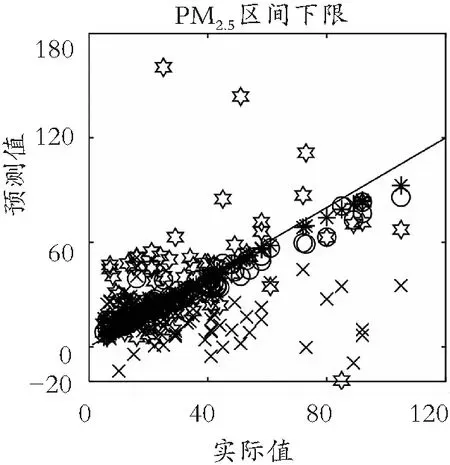
(a) 下限预测效果对比

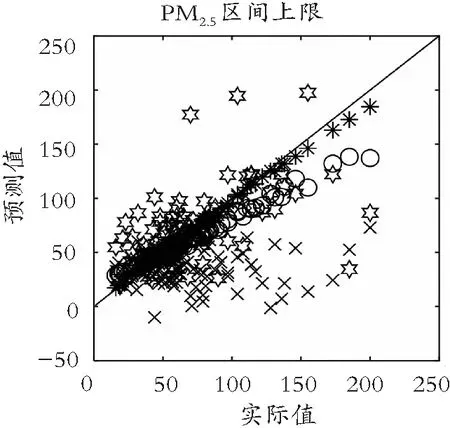
(b) 上限预测效果对比图9 本模型与其他预测方法比较图

另外，本文模型与其他比较模型的预测误差评价指标如表1所示。可以看出，本模型预测误差的各评价指标都低于其他比较模型，进一步反映了本文提出模型的预测精度要高于其他比较模型，具有较好的预测效果和较强的适应性。

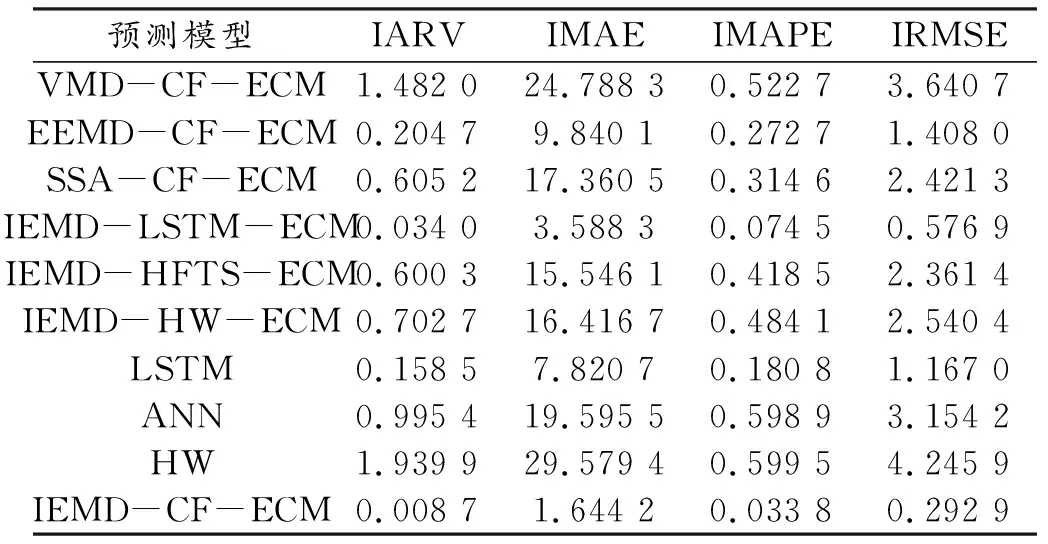
表1 10种预测方法预测误差评价指标对比

综上所述，本研究具有以下3方面的优势：第一，本文提出的区间时间序列组合预测模型可以对PM2.5浓度值变化趋势和范围进行更好预测，克服了传统点值时间序列预测波动信息损失的缺点；第二，本文将深度模型LSTM与区间多尺度分解等方法相结合，提出了一种区间时间序列组合预测框架，能够从大量复杂的时间序列数据中提取关键性的数据特征，克服了传统预测模型存在的滞后性问题；第三，本文通过提取组合预测预测误差提供的有效信息，进行误差修正，使预测精度得到了进一步地提升。

5 结束语

PM2.5浓度值是一个连续变化、随机性强、波动频率不规律的时间序列，传统的日均值分解预测模型很难准确地获取高频序列中的随机性特征，也无法完全体现PM2.5的区间变化规律。因此，本文提出了一种新的基于LSTM-HFTS-EC的PM2.5区间多尺度组合预测模型方法，首先利用IEMD将PM2.5区间时间序列进行分解，再基于Holt-Winters模型、HFTS和LSTM模型分别对分解出的区间趋势序列、低频波动序列和高频波动序列进行预测，并将预测结果集成为PM2.5的区间预测值。进而利用LSTM模型对PM2.5区间预测值进行误差修正，得到PM2.5的最终区间预测结果。最后通过实证预测分析，说明本文的方法适用于具有较大波动的PM2.5区间预测，与已有方法相比具有更高的精确度和良好的适用性。此外，本文的研究也为预测其他具有连续变化和波动范围大特征的实际问题提供了一种新的思路。