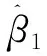工具变量线性回归模型的指数平方损失估计

2022-04-08杨宜平

重庆工商大学学报（自然科学版） 2022年2期

张巍，杨宜平，2

(1. 重庆工商大学数学与统计学院, 重庆 400067;2. 重庆工商大学经济社会应用统计重庆市重点实验室, 重庆 400067)

0 引言

回归分析是研究各种现象之间数量关系的一种常用方法，其中最常见的回归模型是线性回归模型：

其中，Yi∈R是独立同分布的响应变量，Xi∈Rp是p维协变量，β是未知的参数向量。线性回归模型的估计方法层出不穷，最经典的即为最小二乘法，但该方法对误差分布要求较为严苛，如零均值、同方差假定等。在实际应用场景中，最小二乘估计的效果并不理想。为了弥补最小二乘法的不足，Wang 等[1]提出了基于指数平方损失目标函数的估计方法。该方法不需要对模型误差分布作特定的限制，且估计的稳健性由调节参数h控制。该方法一经提出即受到了广泛的关注。Yu等[2]讨论了半函数线性模型的指数平方损失估计，并指出如果随机误差服从重尾分布，该方法比最小二乘法更加有效；Jiang[3]将该方法应用于部分线性模型，并表示当数据集中存在离群点时，该方法得到的参数估计量标准差和均方误差皆优于现有的其他方法。

当前关于指数平方损失方法的研究，多数文献都假定协变量是外生变量，然而在实际应用中，协变量是内生变量的情况不在少数。这种情况下，如果将协变量视为外生变量进行估计，则得到的参数估计量将不再是无偏估计。为了消除内生性带来的影响，Ashenfelter[4]提出了倍差法，Thistlethwaite等[5]提出了断点回归方法，Donald[6]研究了工具变量法。受到Yang等[7]基于工具变量对含测量误差的线性模型进行参数估计的启发，本文基于工具变量的指数平方损失方法对含内生变量的线性模型进行参数估计。

首先给出了估计过程以及调节参数h的选取过程；进一步，在一些正则条件下，研究了估计的渐近性质，然后通过模拟研究，比较了不同误差分布、不同样本量下朴素M估计、朴素最小二乘估计、朴素指数平方损失估计以及基于工具变量的M估计、基于工具变量的最小二乘估计、基于工具变量的指数平方损失估计等6种方法的优劣；最后，利用提出的方法对孪生双胞胎“收入-教育程度”数据进行了实证分析。

1 方法与主要结果

考虑如下工具变量线性回归模型：

其中，Xi是p维内生变量，β是p维未知向量，Zi是q维工具变量，满足cov(Zi,εi)=0，Γ是p×q维矩阵，εi,ei是随机误差。下面给出β的两阶段估计过程。

第一阶段，由于E(Ziei)=0，得到Γ的最小二乘估计：

其中，X=(X1,X2,…,Xn)是p×n维矩阵，Z=(Z1,Z2,…,Zn)是q×n维矩阵。于是，得到Xi的估计量：

可以获得β的指数平方损失估计，即

目标函数L(β)中的h是调节参数，控制着估计的稳健性和有效性。对于较大的h，有

此时，该估计类似于极端情况的最小二乘估计。对于较小的h，|εi|值越大，对估计的影响越小，因此，较小的h将限制离群值对该估计的影响，提高估计的稳健性。下面给出调节参数h的选择过程：

(3) 得到本文所提出估计的渐进方差估计为

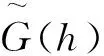
2 渐近性质

且G(x,h)，F(x,h)关于x连续，F(x,h)<0。

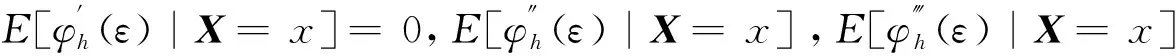
定理1 如果条件C(1), C(2), C(3)皆成立，β0是β的真实值，则

其中，

(1)

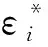
进而可以得到：

随之推出:

(2)

于式(2)，首先考虑式(2)右边，将其在εi点泰勒展开，有

op(1)≜I1+I2+op(1)

再考虑式(2)的左边，有

则可以推出：

易知：

且有

再由中心极限定理，就完成了该定理的证明。

3 数值模拟

本节通过模拟研究评估所提出的IVESL估计量的有效性与准确性，作为比较，还计算了朴素M 估计(nM)、朴素最小二乘估计(nLS)、朴素指数平方损失估计(nESL)、基于工具变量的M估计(IVM)、基于工具变量的最小二乘估计(IVLS)等5种方法的估计量。上面所指的朴素方法指不使用工具变量Zi，直接将Xi视为外生变量参与模型的估计方法。模拟数据来自下列模型：

其中，Xi1～N(0,1)，(β1,β2)T=(5,2)T，Zi～N(1,1)，γ=1，ei～N(0,0.42)，εi=ei+σi。由此可见，Xi1是外生变量，Xi2是内生变量。在本次模拟中，考虑σi的分布为正态分布、T分布和柯西分布，样本容量n=100,150,200，重复运行1 000次，比较不同误差分布情形下6种估计方法的均值、偏差和标准差，模拟结果见表1—表3。从表1—表3可以看出：

(1) 3种基于工具变量的估计方法优于3种朴素估计方法。由此可见，忽略内生变量直接采用X所获得的估计量是有偏的。

(2) 当σi服从正态分布时，3种基于工具变量的估计方法所得估计量的偏差、标准差相差不大；当σi服从T分布或柯西分布时，IVLS方法失去了稳健性，造成了过大的偏差和标准差，IVM和IVESL 方法依然稳健。大多数情况下，IVESL方法略优于IVM方法，因此，本文提出的IVESL估计具有稳健性。

(3)样本容量n增大时，IVM和IVESL估计量的偏差、标准差逐渐下降。

进一步，为了研究本文提出模型在高杠杆点存在的情况下是否依然有效，模拟了在σi服从正态分布的情况下，考虑15%样本点的值为高杠杆点Xi1=3的情况，模拟结果见表4。从表4可以看出：3种朴素方法以及IVLS方法的效果较差，不再适用，而IVM，IVESL方法效果较好，估计量仍然稳健，且IVESL估计量略优于IVM估计量。

因此，本文提出的IVESL方法不需要对模型误差分布作特定的假设，无论模型误差的分布是何种形式，都具有较好的性质，并且，IVESL有效地处理了内生性问题，使得估计量仍然具有无偏性。

表1 随机误差σi～N(0,0.42)的数值模拟结果

表2 随机误差σi～0.2T(2)的数值模拟结果

表3 随机误差σi～0.2Cauchy(2)的数值模拟结果

表4 随机误差σi～N(0,0.42)且15%样本点为高杠杆点Xi1=3的数值模拟结果

4 实例分析

本节用提出的方法对“收入-教育程度”数据进行实证分析。该数据来源于Ashehfelter和Krueger[9]关于同卵双胞胎教育回报率的调查。在这项调查中，包含了149 对同卵双胞胎的样本。Ashehfelter和Krueger使用均值回归模型调查基因遗传对采访到的双胞胎收入与受教育程度的影响。如果用传统方式来量化受教育程度，则该变量会存在内生性，由此导致估计量产生偏差。因此，工具变量的引入可以较好地解决这个问题，构造下列工具变量线性回归模型：

其中，w1是孪生长子的报告收入，w2是孪生次子的报告收入，E1,1是孪生长子报告的所受学校教育年数，E2,2是孪生次子报告的所受学校教育年数。文献[9]分析该数据时，认为每对双胞胎受教育程度之差，即E2,2-E1,1是内生变量，为了消除内生性，采用E2,1-E1,2作为双胞胎受教育程度之差的工具变量，其中，E1,2是孪生长子报告的孪生次子所受学校教育年数，E2,1是孪生次子报告的孪生长子所受的学校教育年数。图1 呈现了响应变量Y的直方图与密度函数曲线，显然，响应变量在右端有显著的重尾效应，根据Kolmogorov-Smirnov 检验得到的P值远小于0.000 1，因此，与最小二乘法相比，采用IVESL方法分析该数据更加合理。为了对比，利用第3节模拟研究的其余5种方法也分析了该数据，计算结果见表5。