集值优化问题近似Henig真有效点的稳定性
2022-04-08胡瑞婷
胡 瑞 婷
(重庆工商大学 数学与统计学院,重庆 400067)
0 引 言
集值优化问题是优化领域的研究热点之一,具有广泛的应用前景。 譬如在物流配送、工程设计、经济金融、环境保护等重大决策和管理活动中都存在大量的集值优化问题。 由此可见,集值优化问题是十分贴近实际生活的一类数学模型,它的研究还涉及凸分析、泛函分析、线性与非线性分析、非光滑分析、变分分析等数学分支, 因此研究集值优化问题具有重要的理论意义。 近年来,国内外众多学者对集值优化问题及其相关问题的理论、算法与应用进行了研究,得到了一系列的重要成果[1-6]。 随着集值优化问题研究的关注度越来越高,其有效解的研究也越来越受国内外学者的重视。 学者们获得了多个不同意义下的真有效解,如Henig真有效解、Benson真有效解、超有效解等。 其中,超有效解的存在条件非常强,Benson真有效解的标量化要求序锥有紧或弱紧的基底。 很多情况下,这些条件都无法达到。 但是,Henig真有效解不仅具有超有效解的一些主要特征,其存在性条件比也超有效解弱,只需要序锥有基底即可。 因此,研究Henig真有效解既有一定的理论价值又有重要的实际意义。 目前学者们关于集值优化问题Henig真有效解的研究主要集中在高阶最优性条件[7]、连通性[8]、带约束的向量平衡问题[9]等,关于其稳定性的研究较少,而稳定性研究有助于提高数值计算分析的精确度,故值得进一步探索。
Lucchetti和Miglierina[10]首次研究了向量优化问题在给定空间及其映像空间下扰动问题的Painlevé-Kuratowski收敛性,为后续学者研究各种解的稳定性奠定了坚实的基础; Zeng等[11]在C凸条件下,讨论了向量优化问题有效点在近似问题的数值Painlevé-Kuratowski收敛致原始问题数值时的稳定性,从而改进了文献[10,12]获得的相应向量优化问题的稳定性定理;Li等[13]在(严格)真拟C凸条件下,利用向量值函数序列的连续性和ΓC收敛性,研究了向量优化问题Henig真有效点集与解集的收敛性,所得结果与文献[10,11]不同。 这类文献对本文集值优化问题近似Henig真有效点的稳定性研究提供了重要的理论支持。
又由于大多数实际问题难以得到准确解,只能用近似解逼近,而近似解不仅使计算精度变高,而且还能适应各种复杂情况。 因此,本文针对集值优化问题近似Henig真有效点,提出在目标集值优化问题的映射及可行域均扰动的情形下,建立C凸集值优化问题近似Henig真有效点的稳定性结果,将近似Henig真有效点的稳定性研究从向量值优化问题推广到集值优化问题中,从而得到新的抗干扰性结果。
1 预备知识
本节将介绍一些基本概念和相关性质。 令C为Rp中内部非空的尖闭凸锥,Rp中C诱导的偏序如下:
y≤Cx⟺x-y∈C,∀x,y∈Rp
y 设F:E→2Rp为集值映射,E为Rm中的非空子集,考虑如下集值优化问题: (E,F):minx∈EF(x) 首先回顾关于集值优化问题(E,F)的几种解的定义,令F(E)=∪x∈EF(x)。 定义1 设E⊂Rm非空,y∈F(E), 任取e∈intC,ε≥0,若点y满足(F(E)-{y}+εe)∩(-C)={0},则称点y为集合F(E)的εe-近似有效点,记集合F(E)中所有εe-近似有效点构成的集合为εe-MinF(E)。 定义2[6]设E⊂Rm非空,y∈F(E),任取e∈intC,ε≥0, 若点y满足(F(E)-{y}+εe)∩(-intC)=∅,则称点y为集合F(E)的εe-近似弱有效点,记集合F(E)中所有εe-近似弱有效点构成的集合为εe-WMinF(E)。 定义3 设E⊂Rm非空,y∈F(E),任取e∈intC,ε≥0, 若存在满足C{0}⊂intC1的内部非空的尖闭凸锥C1,使得(F(E)-{y}+εe)∩(-C1{0})=∅,则称点y为集合F(E)的εe-近似Henig真有效点,记集合F(E)中所有εe-近似Henig真有效点构成的集合为εe-HMinF(E)。 注1 显然εe-HMinF(E)⊂εe-MinF(E)⊂εe-WMinF(E)。 性质1 设e∈intC,ε≥0,则有εe-HMin(F(E)+C)=εe-HMinF(E)。 证明先证εe-HMin (F(E)+C)⊂εe-HMinF(E)。 任取y∈εe-HMin (F(E)+C),则有(F(E)+C-{y}+εe)∩(-C1{0})=∅。 因为F(E)⊂F(E)+C,所以(F(E)-{y}+εe)∩(-C1{0})=∅。 从而可知,y∈εe-HMinF(E),故εe-HMin (F(E)+C)⊂εe-HMinF(E)。 下证εe-HMinF(E)⊂εe-HMin (F(E)+C)。 任取y∈εe-HMinF(E),则有(F(E)-{y}+εe)∩(-C1{0})=∅。 反证法:假设y∉εe-HMin(F(E)+C),则存在y′∈F(E)+C,使得y′-y+εe∈-C1{0},由y′∈F(E)+C可知,存在y″∈F(E),e′∈C,使得y′=y″+e′,从而有y″+e′-y+εe∈-}-C1{0},因此y″-y+εe∈-e′-C1{0},即y″-y+εe∈-C-C1{0}。 又因为C{0}⊂intC1,所以y″-y+εe∈-C1{0},又因为C1为内部非空的尖闭凸维,C1+C1{0}=C1{0},所以y″-y+εe∈-C1{0}。这与y∈εe-HMinF(E)矛盾。 因此y∈εe-HMin(F(E)+C)。 下面回顾集合的Painlevé-Kuratowski收敛性定义。 下面介绍3种集值映射序列收敛的概念。 2) 对任意x∈E,y∈F(x),存在En中的序列{xn},xn→x,有yn∈Fn(Xn),使得yn→y; 3) 对任意x∈E,En中的任意序列{xn},xn→x,和任意ε∈intC,存在kε∈N,使得Fn(xn)+ε⊂F(x)+intC,∀n≥kε。 注3 文献[14,注2.8]中ΓC收敛的向量值形式是定义7的特殊形式;定义6中连续收敛强于定义7中ΓC收敛。 下面讨论集值映射序列连续收敛和Painlevé-Kuratowski收敛之间的关系。 证明先证epiF⊂limninfepiFn。 任取(x,z)∈epiF,则x∈E,z∈F(x)+C。由定义7中2)可知,存在En中序列{xn},xn→x,使得Fn(xn)→F(x)。 因为z∈F(x)+C,所以存在y∈F(x),使得z-y∈C。 令e∈C,e=z-y,则 y=z-e (1) 因为y∈F(x),Fn(xn)→F(x), 所以存在yn∈Fn(xn),使得yn→y。 由式(1)可知yn→z-e,从而有yn+e→z。 令zn=yn+e,则有zn∈Fn(xn)+C且zn→z。 综上可知,存在(xn,zn)∈epiFn,(xn,zn)→(x,z)。 因此(x,z)∈limninfepiFn。 注4 根据性质2易知,Painlevé-Kuratowski收敛弱于ΓC收敛。 下面介绍几种凸性定义、回收锥定义及相关性质。 定义8[13]设E⊂Rm为非空凸集,若F:E→2RP为C凸集值映射,当且仅当对任意x,y∈E,λ∈[0,1],有 λF(x)+(1-λ)F(y)⊂F(λx+(1-λ)y)+C 定义9[6]设E为Rm上的子集,F:E→2RP为集值映射, 对向量α∈RP,F在高度α下的子水平集Fα定义为 Fα={x∈E:α∈F(x)+C} 定义10[10]设闭凸集E⊂Rm,E的回收锥集合定义为 0+(E)={d∈Rm:x+td∈E,∀x∈E,∀t≥0} 注5显然,若闭凸集E⊂Rm,有0+(E)={0},当且仅当E为有界集。 HMinE⊂limninfHMinEn 引理2 令E⊂Rm是闭凸子集,F:E→Rm是连续C凸映射,若对任意α∈Rp,当Fα≠∅时,有 0+(Fα)={0},则F(E)+C为闭集。 证明令序列{yn}⊂F(E)+C且yn→y,下证y∈F(E)+C。 因为{yn}⊂F(E)+C, 所以存在{xn}⊂E,使得yn∈F(xn)+C。 又因为对任意ε∈intC,存在nε∈N,使得y+ε∈yn+C,∀n≥nε, 所以y+ε∈F(xn)+C,∀n≥nε。 由α的任意性,可知0+(Fγ+ε)=0+(Fα)={0}。 再结合注5可得Fγ+ε为有界集,故{xn}收敛。不妨设xn→x,因为y+ε∈F(xn)+C,所以存在ε′∈C,使得y+ε-ε′∈F(xn),从而(xn,y+ε-ε′)→(x,y+ε-ε′)。 又因为F是连续映射,所以y+ε-ε′∈F(x),即y+ε∈F(x)+C, 结合ε的任意性,可知y∈F(x)+C。 因为xn∈E,E为闭集,所以E中{xn}的极限点x∈E,从而y∈F(E)+C,故F(E)+C为闭集。 引理3 若F为Rm中凸子集E上的连续C凸映射,则F(E)+C为凸集。 证明任取y1,y2∈F(E)+C,λ∈[0,1],则存在x1∈E,使得y1∈F(x1)+C,存在x2∈E,使得y2∈F(x2)+C,所以λy1+(1-λ)y2∈λF(x1)+(1-λ)×F(x2)+C。 由F的C凸性,可知λF(x1)+(1-λ)×F(x2)⊂F(λx1+(1-λ)x2)+C,因为E为凸集,所以λx1+(1-λ)x2∈E,从而有λy1+(1-λ)y2∈F(E)+C+C⊂F(E)+C,所以λy1+(1-λ)y2∈F(E)+C,由此可知F(E)+C为凸集。 本节在集值优化问题的可行域和目标映射均扰动的情况下,建立集值优化问题近似Henig真有效点的Painlevé-Kuratowski抗干扰性收敛性结果。 (2) 其中,B(0,r)表示以0为球心,r为半径的球。 d(xnk,Fα)>r (3) α∈y′+C (4) (5) 综上所述,式(2)成立。 (xk,γk)→(x,γ) (6) 其中,xk∈Enk且 γk∈Fnk(xk)+C (7) 由式(6)可知γk→γ,并对任意ε∈intC,存在kε∈N,使得 γ+ε∈γk+C,∀k>kε (8) 又由式(7)和式(8),可得 γ+ε∈Fnk(xk)+C,∀k>kε 即当k充分大时,有 (9) 性质5 设E⊂Rm为非空闭凸子集,F:E→2RP为E上的C凸集值映射且epiF为闭集, 则以下命题等价: 1)α∈Rm,当Fα≠∅时,0+(Fα)={0}; 2)α∈Rm,当Fα≠∅时,Fα有界。 证明与文献[6,引理3.6]证明类似,稍作修改即可得正。 下面建立扰动集值优化问题εe-近似Henig真有效点的稳定性结果。 定理1假设性质3的所有条件都满足,且Fn在En上连续,则HMinF(E)⊂limninfHMinFn(En)。 受文献[13]的启发,将Henig真有效点推广到近似Henig真有效点,且将近似Henig真有效点的稳定性结果从向量优化问题推广到C凸集值优化问题的情形中。 在扰动集值优化问题的问题数据Painlevé-Kuratowski收敛到目标集值优化问题的问题数据情况下,获得了集值优化问题近似Henig真有效点的抗干扰稳定性结果。 该结果对数值计算分析中集值优化问题近似Henig真有效点的稳定性研究有着重要的理论价值。



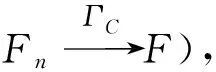



2 稳定性结果





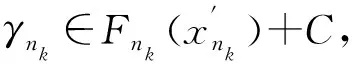






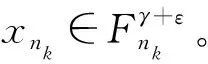

3 结束语
