融合功率分配策略的NGSO-GSO频率干扰计算方法研究

董苏惠, 潘 冀, 姚秀娟, 高 翔, 闫 毅, 智 佳

(1. 中国科学院国家空间科学中心, 北京 100190; 2. 中国科学院大学, 北京 100049;3. 国家无线电监测中心, 北京 100037)

0 引 言

由于低轨宽带互联网星座系统可以实现全球通信的无缝覆盖,且具有频谱利用率高、通信时延短、通信容量大的特点,成为近几年来卫星通信领域的发展热点,典型如StarLink星座系统、OneWeb的星座系统、Telesat的星座系统等[1-3]。卫星星座系统的大量部署使空间频谱和轨道资源异常紧张,特别是大规模非对地静止轨道(none geostationary satellite orbit, NGSO)卫星星座系统对地球静止轨道(geostationary satellite orbit, GSO)卫星系统的频率重叠问题严重,迫切需要探索有效、实用的干扰分析方法,为它们之间的频率兼容性共存提供技术支撑。

国内外针对NGSO与GSO系统间的兼容性分析已经开展了很多研究工作,具有较高的指导意义[4-6],其中文献[4]主要研究了缓解NGSO系统对GSO系统的共线干扰,文献[7-11]主要通过空间特征中的空间隔离来避免干扰,如提出地球站的隔离角和划分干扰规避区域,文献[12]则通过划分信道的方式来实现频谱的复用,文献[13]通过基于距离和业务流量认知的功率控制方法抑制了NGSO系统对GSO系统的干扰,文献[14]研究了频率复用因子为7的多波束GSO和NGSO卫星共存的认知卫星系统,所提波束功率控制方法在保证GSO用户服务质量约束下,提高了NGSO卫星的吞吐量,文献[15]针对GSO和NGSO的双星系统提出一种基于频率动态分配的频谱共享方法。但由于技术发展和实验条件的限制,融合功率分配策略的NGSO-GSO系统间的频率干扰分析方法的研究较少。

本文在考虑了GSO系统与NGSO星座的空间特征、波束业务特征及信道特征的基础上,针对GSO卫星系统和NGSO星座系统分别提出了对应的融合了带宽和波束特征的功率分配策略。并在下行及上行干扰分析场景中构建了相应分配策略的目标函数和约束条件,在满足空间隔离条件下,分析比较了不同分配策略对NGSO-GSO间干扰噪声比I/N的影响效果,所提方法对缓解NGSO星座对GSO系统的干扰具有一定的作用,为NGSO-GSO间的频率兼容分析提供一种参考。

1 基于空间特征的功率分配方法

1.1 链路分离角

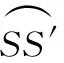
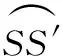
(1)

(2)

则链路分离角α可由下式计算得到：

(3)

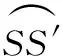
1.2 基于链路分离角的干扰场景构建

如图2和图3所示,GSO卫星由于南北偏移θ角度的轨道摄动,会产生GSO带。在图2下行场景中,当NGSO星座中的卫星与GSO卫星、GSO地球站三者共线时,GSO地球站接收到NGSO卫星的下行干扰达到最大值[4-5],此时NGSO卫星对GSO卫星产生的干扰称之为最坏干扰。在图3上行链路分析场景中,NGSO卫星波束覆盖范围内的多个地球站的上行天线波束会对GSO卫星产生集总干扰。

当NGSO地球站的链路分离角α小于某一阈值αth时,NGSO星座系统需要采取波束关闭或切换或降低发射功率的操作,以降低NGSO星座系统对GSO系统的同道干扰[10]。

2 上下行通信链路建立条件

在同向上行或下行链路干扰分析场景中,由于NGSO星座系统的链路复杂性,会有多条来自NGSO系统的干扰链路对GSO系统的接收机造成干扰,因此主要考虑NGSO星座系统对GSO卫星系统造成的集总干扰。那么GSO系统的接收机接收的集总干扰噪声比(interference to noise ratio, INR) ∑I/N表示为

(4)

式中:Numngso为干扰系统的发射机总数;Mi为干扰系统中第i个发射机的干扰链路建立的总数;N为受扰系统接收机的等效噪声功率;(I/N)i, j为干扰系统第i个发射机建立的第j条干扰链路上的干扰噪声比。其中,(I/N)ij可由下式[4]计算得到:

(5)

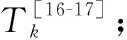
(6)

式中:gtx,max为该卫星系统天线最大发射增益;gre,max为该卫星系统天线最大接收增益;lk为第k个波束建立的通信链路的损耗,具体为

(7)

式中:fk为第k个波束的中心通信频率,单位为Hz;ds→es为星地链路的距离,m;Ar,k为星地链路中降雨引起的衰减值,单位为dB;Ac,k为星地链路中云雾引起的衰减值,单位为dB[18]。

3 功率分配目标函数构建方法及效果分析

为便于分析,被干扰GSO卫星上行通信链路选取CHNNEWSAT-G1-118E和101.5E卫星在ITU登记的上行KAUWB波束和空口参数;下行通信链路选取CHNNEWSAT-G1-118E卫星的下行KADWB波束和空口参数[19],如表1所示。干扰NGSO星座系统则参考OneWeb星座的轨道构型,即轨道高度为1 200 km的18个轨道平面共计720颗卫星,波束及空口参数依据其在ITU登记的上行GRA波束和下行GTA波束信息[20],频率范围选择与GSO卫星频率重叠的部分,如表2所示。

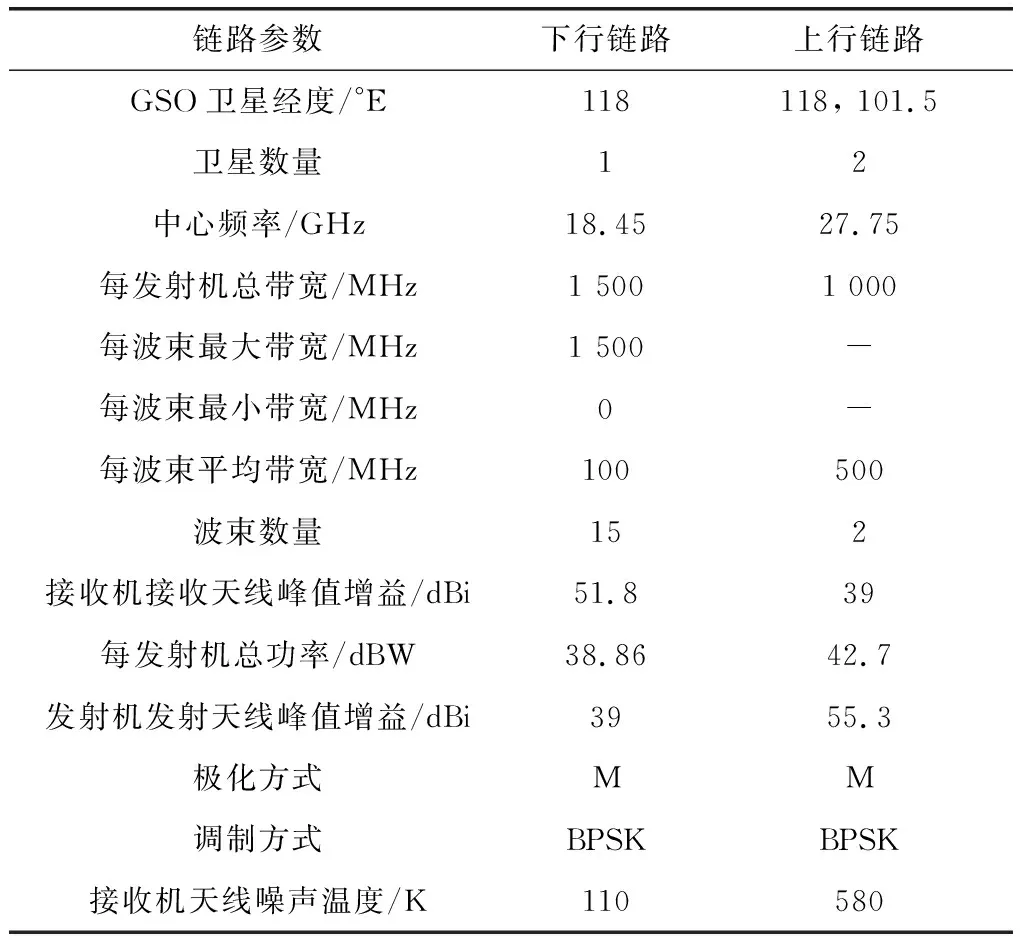
表1 GSO系统上行及下行链路轨道、波束及空口参数Table 1 Orbit, beam and air interface parameters of GSO systems for uplink and downlink

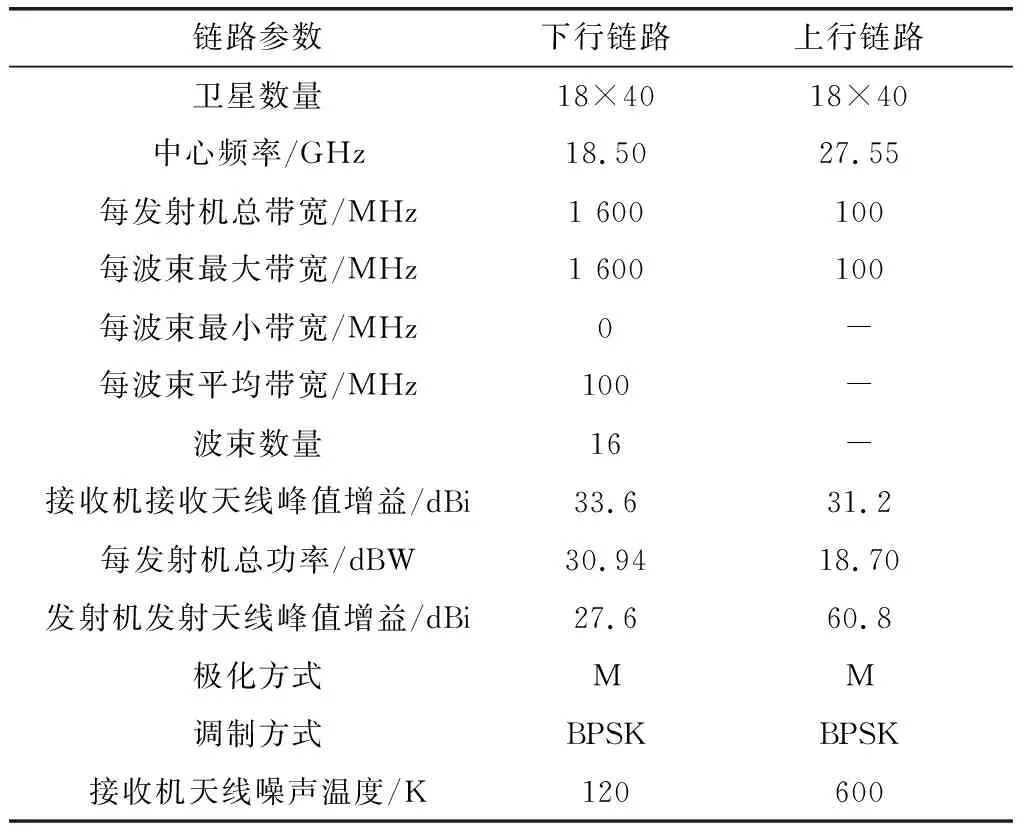
表2 NGSO系统上行及下行链路波束及空口参数Table 2 Beam and air interface parameters of NGSO systems for uplink and downlink

3.1 下行链路目标函数构建方法

本节对下行通信链路功率分配方法的研究主要基于系统信道容量的公平性分配原则。在对带宽和功率资源分配时,结合GSO卫星系统和NGSO星座系统各自建链的特点和复杂性,考虑下行链路不同波束覆盖区域的业务需求量的差异,针对性设计相匹配的功率分配策略。

3.1.1 GSO卫星系统下行链路目标函数构建

受扰多波束卫星系统第k个波束建立的通信链路的信道容量Rk为

(8)

为追求系统资源分配的公平性,结合GSO卫星系统通信链路拓扑结构的相对固定性,可将多波束GSO卫星系统业务需求量Tk和链路的信道容量Rk的偏差作为待优化的目标函数,具体形式为

(9)

本节涉及的不同波束业务需求量与波束覆盖的中心区域的人口流量成正比[17],基于式(9)所示的目标函数,可以采用带宽和功率的联合分配(joint bandwidth and power allocation, JBPA)策略[21],对应的约束条件[21]为

(10)

此外,如果考虑多波束业务的实时性,还需要考虑波束的时延特征。多波束GSO卫星系统第k个波束的平均最大容许时延限制Dk[22-23]为

(11)

式中:ek为第k个波束建立的通信链路的误包率(packet error rate, PER)。

在式(9)的基础上,将GSO卫星系统的多波束容许时延限制Dk作为非线性约束条件,采用考虑时延的带宽和功率联合分配(time delayed bandwidth and power allocation, TD-BPA)策略[22-23]时,对应的约束条件如下:

(12)

本文将这种融合干扰、业务需求量及链路建立条件的带宽和功率分配策略称之为多特征融合的功率分配(multi-feature fused bandwidth and power allocation, MFF-BPA)策略,采用该策略构建的目标函数为

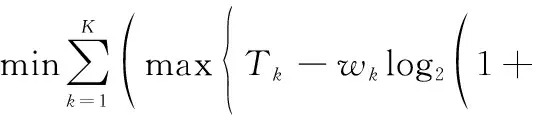
(13)

则MFF-BPA策略的约束条件为

(14)

上述构建的非线性规划问题可以通过采用拉格朗日对偶理论的次梯度求解法来求解[21,23-25],该法可以寻找到优化问题的最优解和近似解,但算法求解的收敛速度较慢。本节在功率受限的条件下,在点波束所在区域业务需求高于容量环境下进行资源分配,依据式(13)和式(14)构建的拉格朗日函数J(·)为

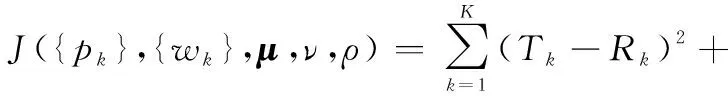
(15)

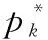
(16)

(17)

J(·)对pk和wk的偏导函数为

(18)

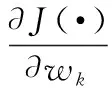
(19)

式中:

(20)

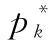
(21)

式中:step为迭代次数,当Δpk<ε1和Δwk<ε2时停止迭代。并利用梯度法更新μk,ν和ρ的值,可以得到

(22)

式中:[·]+=max(·,0);Δstep为迭代步长。根据式(15)～式(22),MFF-BPA策略求解算法如算法1所示。

下述求解目标函数问题也可以转换为求解凸优化问题,参考算法1求解算法,进而实现求解目标函数。

算法 1 MFF-BPA策略求解算法输入:表1的波束及空口参数,ε1,ε2输出: {pk}和{wk}最优分配p*k,w*k1: initialize: p0k, w0k;∥初始化各波束分配的功率和带宽值2: initialize: μ0k,υ0,ρ0;∥初始化拉格朗日因子3: repeat∥开始迭代4: calculate pstep+1k,wstep+1k;∥利用牛顿迭代法5: ifΔpk<ε1&&Δwk<ε2, then6: break7: else8: update μstep+1k,νstep+1,ρstep+1;∥更新拉格朗日因子9: update pstep+1k,wstep+1k;10: end if11: p*k←pstep+1k;12: w*k←wstep+1k;13: return p*k,w*k

3.1.2 NGSO星座下行链路目标函数构建

NGSO星座系统具有星座规模巨大和链路复杂的特点,通信链路的建立和断开也具有高动态性,因而,通信资源的分配具有较高的复杂性。由于业务类型和用户数量众多,系统容量是星座系统建设及运行中需要考虑的关键因素之一。故而,本文主要将多波束NGSO星座系统容量的最大化作为待优化的目标函数,具体形式为

(23)

式中:L为每个卫星发射机发射的波束个数。

参考第3.1.1节GSO卫星系统波束的功率分配策略,对NGSO星座系统有限的功率和带宽资源进行分配,基于式(23)所示的目标函数,采用JBPA策略对应的约束条件为

(24)

相似地,依据第2节提出的建链条件,忽略小于链路建立阈值[C/N]th的次要载波,可以降低频率干扰仿真中的运算量。该策略称之为融合干扰及建链条件的带宽和功率分配(interference and link fused bandwidth and power allocation, ILF-BPA)策略,则该策略的目标函数为

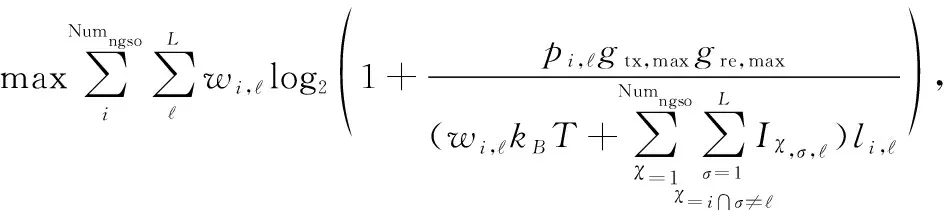
(25)

为了避免式(25)中信道容量最大化的分配策略所产生的功率分配失衡现象,在ILF-BPA策略的约束条件中对这种现象进行了补偿和改善,其形式为

(26)

3.2 上行链路目标函数构建方法

上行链路的功率分配主要考虑如何缓解上行链路信道衰落带来的影响,以保证链路的通信质量。

3.2.1 GSO卫星系统上行链路目标函数构建

参考第3.1节下行场景,假设上行多波束GSO卫星系统的地球站共有Numgso个发射机,每个发射机有K个波束为视距内多个不同的GSO卫星提供服务,信道容量矩阵R为

∀k∈K;∀ξ∈Numgso

(27)

式中:Rξ,k为地球站的第ξ个发射机的第k个波束的信道容量。

GSO卫星上行链路的ILF-BPA策略主要基于最小容量最大化的方法[26-27],则对地球站的第ξ个发射机构建的目标函数和约束分别为

(28)

式中:

(29)

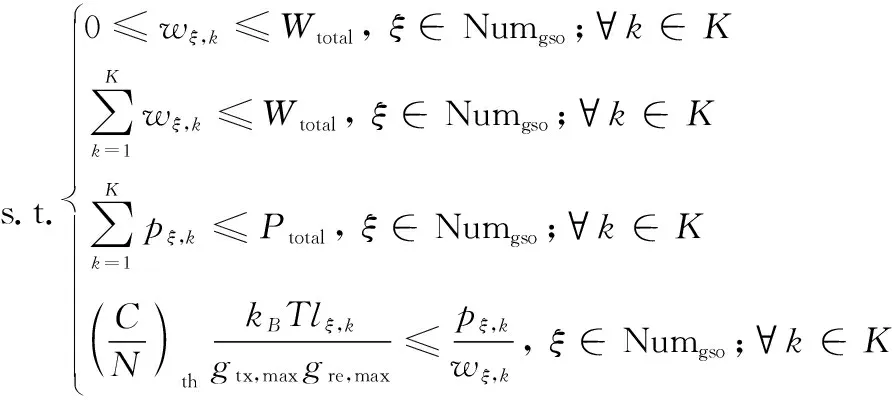
(30)

如式(28)～式(30)所示,该分配策略考虑到了不同信道条件的差异,将最小容量的最大值作为目标函数,并考虑将建链条件作为约束条件之一,保证了信道的可靠通信。

3.2.2 NGSO星座系统上行链路目标函数构建

与GSO卫星系统上行场景相似,针对NGSO星座的ILF-BPA策略也可以采取基于最小容量最大化的方法[26-27],其中Numngso为NGSO星座系统中上行链路干扰地球站的发射机总数,每个发射机有L个波束为视距内多个不同的NGSO卫星提供服务,则NGSO系统中地球站的第i个发射机构建的目标函数和约束为

(31)

式中:

∀∈L；∀i∈Numngso；∀σ∈L；∀χ∈Numngso

(32)

(33)

3.3 下行及上行链路构建的目标函数对功率密度的影响研究

3.3.1 下行链路计算结果分析

参考表1中下行链路波束及空口参数,GSO卫星下行15个波束均匀覆盖纬度15°N～50°N范围以及经度85°E～130°E范围,并在波束中心布设下行链路的地球站,则可计算出GSO卫星系统各下行波束业务需求量Tk和链路损耗lk,如图4所示。

依据式(9)、式(10)、式(12)～式(14),采用带宽和功率均匀分配(uniform bandwidth and power allocation, UBPA)、JBPA、TD-BPA及MFF-BPA这4种分配策略,计算得到的GSO卫星系统各波束的功率密度pk/wk值,其中该GSO卫星下行的[C/N]th值为14 dB[19],各波束由于时延引起的最小业务需求量为Tk的20%[23],∑kpk和∑kwk与Ptotal,Wtotal的偏差不超过10-8,如图5所示。

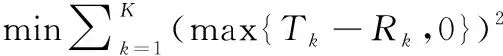
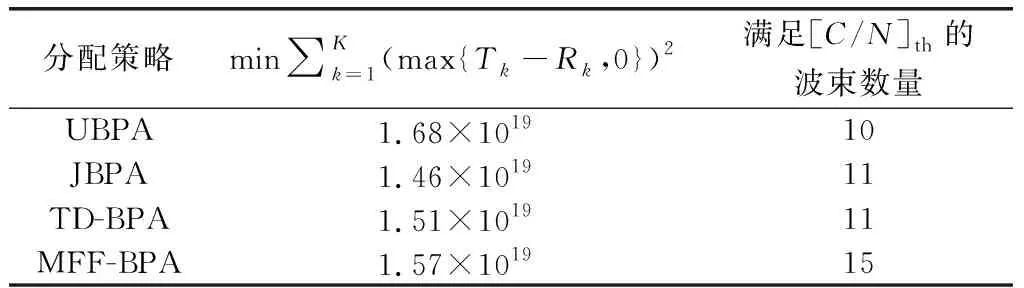
表3 不同分配策略下的GSO卫星下行链路波束目标函数值Table 3 Objective function values calculated by different allocation strategies of the GSO downlink beam

以距表1中GSO卫星最近的一颗OneWeb星座系统的卫星为例,参考表2的下行链路波束及空口参数,该星上发射波束的链路损耗li,以及采用不同分配策略计算得到的该星上各波束的功率密度pi,/wi,值如图6所示, 其中OneWeb卫星在ITU登记的[C/N]th值为10 dB[20],∑pi,和∑wi,与Ptotal,Wtotal的偏差不超过10-8。

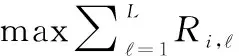
表4 NGSO下行链路波束3种分配策略下的目标函数值Table 4 Objective function values obtained by three alocation strategies of the NGSO downlink beam

图6中JBPA策略分配得到的序号为{1,5,6,8,9,13,14,15,16}的波束无法满足该星在ITU登记的C/N建链的最小值;UBPA策略得到的序号为{1,6,8,9,13,14,15,16}的波束无法满足该星在ITU登记的C/N建链的最小值。

3.3.2 上行链路计算结果分析

依据表1中GSO卫星上行链路波束及空口参数,假设有多个地球站为视距(line of sight, LOS)内的轨道位置为118°E和101.5°E的GSO卫星提供服务,每个地球站的发射机有2个波束,采用星历引导分别跟踪这2颗卫星。假设地球站位于中国的55个主要热点城市,分布情况如图7所示。

依据式(28)～式(30),采用不同分配策略计算得到的每个地球站发射机各个波束的功率密度pξ,k/wξ,k分配情况如图8所示,其中[C/N]th值为14 dB[19],∑kpξ,k和∑kwξ,k与Ptotal,Wtotal的偏差不超过10-8。

图8中,对于JBPA策略,序号为{34,50}的地球站指向118°E GSO的上行波束和序号为{10,19,45}的地球站指向101.5°E GSO的上行波束低于[C/N]th;对于UBPA策略,序号为{42,45}的地球站指向101.5°E GSO的上行波束低于[C/N]th。图9为图8中按照这3种分配策略计算得到的上行链路目标函数最小信道容量Rξ,k的最大值的对比曲线。

考虑到上行链路地球站位置的分布范围,该纬度范围的LOS内的平均OneWeb卫星数目不超过2颗(考虑到FCC文件中报告的最小仰角)[28],其上行链路的功率分配可简单化处理,本文不再赘述。

4 融合功率分配策略对NGSO-GSO间的I/N值评估的影响分析

参考表1和表2的上下行波束空口参数和第3节的方法,对NGSO星座系统与GSO系统的INRI/N进行概率统计计算。

对于下行链路,在受扰GSO卫星系统分别采用UBPA、JBPA和MFF-BPA策略,干扰NGSO星座系统分别采用UBPA、JBPA和ILF-BPA策略条件下,研究INRI/N的时间累积百分比的变化特性曲线,如图10所示;对于上行链路,主要研究受扰GSO卫星系统采用UBPA、JBPA和ILF-BPA策略下的INRI/N的时间累积百分比的变化特性曲线,如图11所示。其中αth=75°,调制方式为BPSK,时间步长为10 s,时长为1 d,NGSO系统星上天线方向图参考建议书ITU-R S.1528[29],GSO星上天线参考建议书ITU-R S.672-4[30],地球站方向图参考建议书ITU-R S.465-6[31]。

图10和图11中的各曲线的INRI/N超过-12.2 dB限值百分比的结果情况如表5所示。

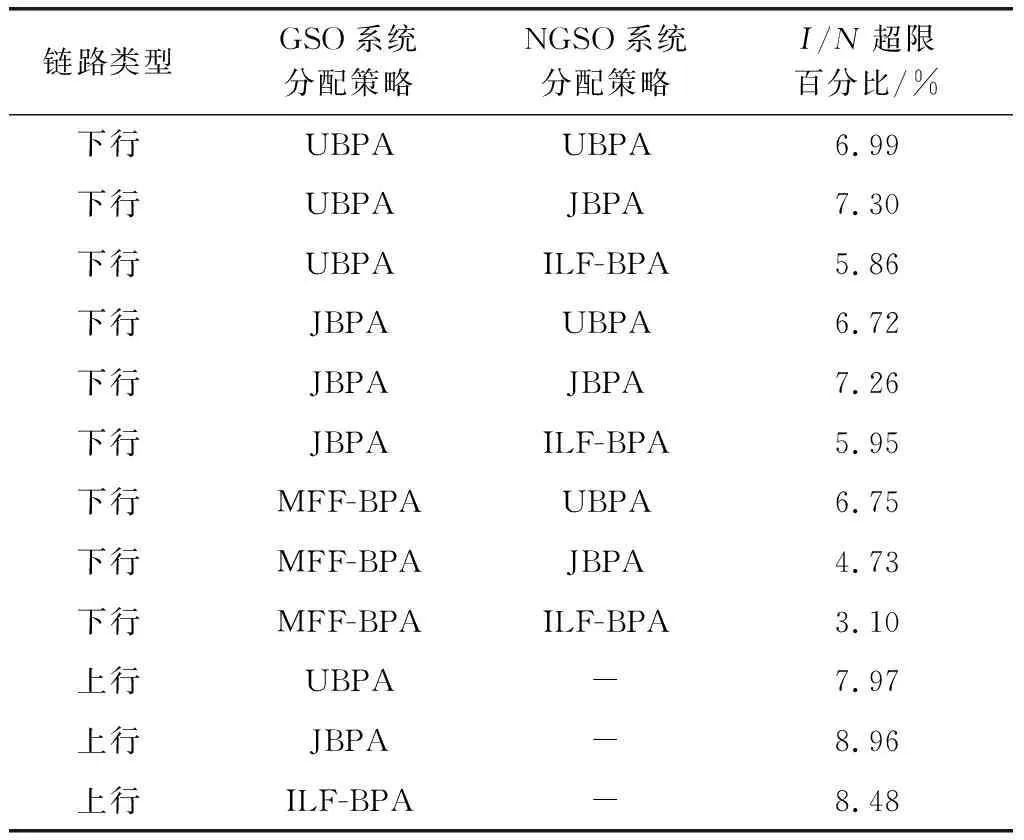
表5 INR I/N超过-12.2 dB限值的对比结果Table 5 Comparison results of the I/N exceeding the limit of -12.2 dB

如表5所示,对于NGSO-GSO上行链路干扰场景,受扰GSO卫星系统每个地球站发射机的波束数量为2的情况下,ILF-BPA分配策略与其他策略的I/N超限百分比偏差不超过0.51%;对于下行链路干扰场景,在受扰GSO卫星系统为同一种分配策略条件下,干扰NGSO星座系统采用ILF-BPA策略,相比于其他两种分配策略,在保证波束满足建链条件的情况下,I/N超限百分比降低了0.77%～3.65%;在干扰NGSO星座为同一种分配策略条件下,受扰GSO卫星采用MFF-BPA策略,相比于其他两种分配策略,I/N超限百分比基本上降低了0.24%～2.85%。

在相同的波束及空口参数条件下,以下行链路为例,考虑到将所提方法与其他相关文献方法就干扰评估效果进行对比分析。图12主要涉及引言部分提到的文献[4,10-11,13-14]所采用的NGSO-GSO频率干扰分析方法。

如图12所示,相比于上述文献,当GSO和NGSO系统同时采用所提的MFF-BPA及ILF-BPA策略时,I/N超限百分比基本上降低了1.41%～3.88%,进一步验证了所提方法的有效性。

5 结 论

在NGSO-GSO干扰场景中:提出了一种考虑融合功率分配策略的干扰计算方法,该方法融合了空间特征、波束业务特征及信道特征,支持系统级的定量化计算分析;针对提出的NGSO和GSO系统的功率分配策略,分别设计了相对应的上下行链路的目标函数和非线性约束,该策略结合了建链特征;定量化对比分析了融合功率分配策略对缓解系统间干扰的作用,在下行链路干扰计算分析时,当干扰NGSO星座分配策略不变时,受扰GSO卫星采用提出的MFF-BPA策略,相比于UBPA、JBPA策略,I/N超限百分比降低了0.24%～2.85%;当受扰GSO系统分配策略不变时,干扰NGSO星座采用ILF-BPA策略,相比于UBPA和JBPA策略,I/N超限百分比降低了0.77%～3.65%。

本文所提出的方法可作为NGSO-GSO系统间下行链路的频率干扰分析的参考。在现有实验条件下,融合功率分配策略对上行I/N超限百分比的缓解作用不明显,后续将进一步研究。此外,本文重点研究Ku/Ka频段的NGSO-GSO系统间的干扰分析,后续将在此基础上,考虑其他频段的频率共用特点和信道特征,进一步探讨缓解NGSO星座对GSO系统干扰的有效手段。