具有多模式球面4R机构结构参数研究

2022-04-07刘宏昭胡旭宇

农业机械学报 2022年3期

刘伟刘宏昭胡旭宇

(1.西安理工大学机械与精密仪器工程学院，西安 710048; 2.西安工程大学机电工程学院，西安 710048)

0 引言

多模式并联机构和多模式混联机构中含具有多模式的单环结构。一些并联机构中含有的多模式单环结构使得并联机构具有多种运动模式。将机构的结构参数看作变量，对单环机构[1]运动模式进行分析时，现有的运动模式分析方法将遇到较大的挑战[2]。多模式单环机构是多模式多环机构的基础，对多模式单环机构的运动模式分析时，将机构的结构参数作为变量，研究结构参数对多模式机构运动模式的影响，是多模式机构创新设计需要解决的重要问题之一。

多模式机构运动模式分析方法基本可分为6类：基于旋量理论、基于数值计算方法、基于高阶运动学分析、基于几何图像方法、基于位移流形理论、基于代数几何方法。①基于旋量理论方法。在机构多运动模式分析时，需要对机构的每种运动模式的运动旋量进行求解[3]。结合给定结构参数，使用旋量理论对其进行运动模式分析比较简便有效，使用该理论研究结构参数对机构运动模式影响的文献较为少见。②基于数值计算方法。过约束机构在折叠结构中应用广泛[4-5]，设计时往往需要对机构在折叠过程中是否发生运动模式变换进行判断。数值计算方法在过约束机构运动学方程不具有解析解时，给定结构参数后，对其运动模式的研究可得到理想的结果。当机构结构参数作为变量时，需要进行大量的计算，不易全面分析结构参数对机构运动模式的影响。③基于高阶运动学方法。基于高阶运动学对机构的多种运动模式进行研究[6-8]，可得一些具有新型运动特征的机构，该方法主要对具有结构参数确定的机构分析其高阶运动特征，主要是通过高阶运动学分析机构的奇异位形运动特性。④基于几何图像方法。根据连杆输出点的空间位置，通过几何图像法对多模式机构模式进行分析[9-10]。通过几何图像分析时，需要先确定机构结构参数，目前多使用该方法在分析具有多种移动运动模式机构所具有的运动模式。然而，机构空间运动较移动运动更为复杂，并且机构结构参数变换时，不容易使用该方法全面研究结构参数对机构运动模式的影响。⑤基于位移流形理论方法。位移流形理论在对机构运动模式分析时的能力较为有限[11-12]，主要是通过机构不同位形下，运动副之间的几何关系，结合机构奇异位形对机构运动模式进行分析。位移流形理论下运动链的表达式中不含有机构的结构参数信息，因此目前这方面的相关研究较少。⑥基于代数几何方法。使用代数几何方法对机构运动模式进行分析，主要是将机构的运动学方程转换为代数方程后，对其对应的仿射簇进行相应的准素分解。文献[13]使用输入变量与输出变量的代数方程系数对平面4R机构进行了分类，将其结构参数与八面体空间中的点建立一个映射关系。文献[14]使用对偶四元数描述机构的约束方程，克服了使用万能代换求解时，需要对关节转角为180°时，单独进行分析的繁琐计算过程。文献[15]分析一般面对称6R机构的运动学方程，得到其具有多种运动模式时，机构参数所满足的条件，对这类6R机构的运动特性进行了全面分析。该方法研究了机构结构参数对一类6R机构运动模式的影响，文中指出存在一部分具有多种运动模式的该类6R机构，并不符合其提出的多运动模式判断依据。文献[16]使用代数计算软件，针对具有不同结构参数的3RER具有的运动模式进行全面分析。代数几何方法在机构运动模式分析时，一般能取得比较理想的结果。然而，由于机构运动学方程和机构结构参数数目的增多，使得机构运动模式分析困难。一方面，变量数目一定程度上决定了运动模式分析的复杂程度；另一方面，复杂的运动模式分析对软件计算[17]的依赖程度较高，文献[18]研究表明，通过软件计算分析机构运动模式时，需要对计算结果进行特殊的分析处理才能得到正确结果，而这个过程较繁琐。

综上所述，基于旋量理论、数值计算、高阶运动学分析、位移流形理论，尚不能全面分析机构结构参数对其运动模式的影响。虽然现有文献中基于代数几何方法可以全面分析机构结构参数对机构运动模式的影响，但是该方法尚不能对机构实际具有的运动模式结果进行全面解释。使用软件分析结构参数对机构运动模式的影响计算量太大，且有时需要对计算结果进行分析才能得到正确结果。

本文使用代数几何理论，基于多项式可因式分解的条件，结合机构的运动模式，提出一种分析结构参数对球面4R机构运动模式影响的方法。

1 确定具有多种运动模式球面4R机构结构参数的方法

一般情况下，将机构运动学方程转换为代数方程后，当机构构型一定时，机构运动学方程的形式和结构基本确定，即运动学代数方程关于关节变量的各个多项式组成即可确定。不同的机构结构参数代入机构运动学方程，从而使得关节变量多项式系数发生改变。如果机构运动学代数方程可以在实数范围内进行准素分解[19]，则该机构具有多种运动模式。那么可以根据机构运动学代数方程分析得到可准素分解的条件，求解代数方程中与机构结构参数有关的系数，从而设计具有多种运动模式的机构。文献[20]指出，对于一个代数方程而言，对该代数方程对应的多项式进行因式分解，即是一种特殊的准素分解。文献[19]给出了判断代数方程是否可以进行因式分解的依据，即该代数方程可写成有理分式的参数方程时，该代数方程可因式分解。

综上所述，可对球面4R机构对应的代数方程判断其是否可转换为有理分式表达的参数方程，对其运动模式进行分析。

使用因式分解方法对多运动模式球面4R机构结构参数对其运动模式影响的分析步骤为：

(1)根据球面4R机构的4个连杆的机构结构参数建立运动学方程

f(θi,θj)=0

(1)

(2)使用万能代换替换球面4R机构转动副关节变量θi、θj的三角函数，化简得到关于关节变量θi、θj的代数方程为

ft(ti,tj)=0

其中

ti=tan(θi/2)tj=tan(θj/2)

(3)将球面4R机构代数运动学方程中各多项式系数，分别置零后组合，得到结构参数满足的公式。

(4)将步骤(3)得到结构参数满足的关系，代入步骤(1)中球面4R机构的运动学方程，分析任意关节变量θi=π时的任意组合下机构具有的运动模式。

(5)将步骤(3)得到的不同结构参数满足的公式，代入步骤(2)中球面4R机构的运动学代数方程，判断该方程是否可进行因式分解，从而分析机构具有的运动模式。

(6)结合步骤(4)、(5)的结果，得到球面4R机构具有不同运动模式时，结构参数满足的关系。

2 球面4R机构运动学方程与多模式结构参数的关系

2.1 球面4R机构运动学方程

如图1所示球面4R机构，4个转动副R1、R2、R3、R4轴线相交于点o，αij为转动副Ri转动轴线zi绕轴线y′i转动到与轴线zi+1重合时的角度。θi为轴线xi绕轴线zi转动到与轴线x′i重合时的角度。可选取转动副R1、R4的关节变量转角θ1、θ4建立运动学方程。文献[21]给出的球面4R机构的运动学计算公式为

图1 球面4R机构结构参数Fig.1 Structural parameters of spherical 4R mechanism

-s12s41c34c1-s12c41s34c1c4+s12s34s1s4-c12s41s34c4+
c12c41c34-c23=0

(2)

式(2)中sij、cij表示αij的正弦和余弦，si、ci表示转角θi的正弦和余弦。式(2)为第1节中步骤(1)中f(θi,θj)=0，i=1，j=4。即式(2)是关于关节变量θ1、θ4的运动学方程。

2.2 球面4R机构运动学方程转变为代数方程

使用万能代换，t1=tan(θ1/2),t4=tan(θ4/2)，将球面4R运动学方程式(2)整理得到

(3)

其中

A=s12s41c34-s12c41s34+c12s41s34+c12c41c34-c23=
c34cos(α12-α41)-s34cos(α12-α41)-c23=
cos(α12-α41+α34)-c23
B=-s12s41c34+s12c41s34+c12s41s34+c12c41c34-c23=
s12sin(α34-α41)+c12cos(α34-α41)-c23=
cos(α12+α41-α34)-c23
C=s12s41c34+s12c41s34-c12s41s34+c12c41c34-c23=
s12sin(α34+α41)+c12cos(α34+α41)-c23=
cos(α12-α41-α34)-c23
D=4s12s34
E=-s12s41c34-s12c41s34-c12s41s34+c12c41c34-c23=
-s12sin(α34+α41)+c12cos(α34+α41)-c23=
cos(α12+α41+α34)-c23

式(3)为第1节步骤(2)中的ft(ti,tj)=0。

2.3 代数方程多项式系数分别置零进行组合

不考虑转动副R1和R2以及R3和R4轴线重合，机构中存在局部转动自由度的情况，因而式(3)中D≠0。

当a12-a41+a34+a23=2kπ(k=0,±1,±2,…,±n)时，式(3)中A为零，该机构自由度为零，这种情况舍去不做分析。同理，可根据式(3)，当A=0,B=0,C=0,E=0时分别可得到

(4)

球面4R机构处于约束奇异位形时，4个转动副轴线共面。关节转角θ1、θ4只存在4种情况(θ1=0°，θ4=0°；θ1=0°，θ4=180°；θ1=180°，θ4=0°；θ1=180°，θ4=180°)时，球面4R机构处于约束奇异位形，此时机构的运动模式将具有改变的可能性。将上述4组数值，代入式(2)，变换为式(3)的代数方程，分别得到E=0，B=0，C=0，A=0。即当该方程系数A、B、C、E分别为零时，球面4R机构具有4个转动轴线在同一平面的机构奇异位形。

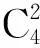
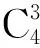
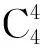
由于转动副R1、R4均连接机架，可将分别满足条件B=0和条件C=0的机构看作一种机构。同理，⑤和⑥、⑨和、和同为一类机构。因而总共可分为11种情况。

3 不同结构参数球面4R机构运动模式分析

根据文献[19]可知，当一个代数方程转变为参数方程后，参数方程均为有理代数分式时，则该代数方程不能被因式分解。从而可对球面4R机构运动学代数方程是否可以进行因式分解进行判断，进而得到球面4R机构的运动模式。

3.1 球面4R机构运动模式(1号A=0)

当a12-a41+a34-a23=2kπ(k=0，±1,±2,…，±n)，且θ1=±π或θ4=±π时，根据式(2)得到，θ4或θ1为定值，此时机构不具有固定轴线转动运动模式。

当a12-a41+a34-a23=2kπ(k=0，±1,±2,…，±n)，且θ1≠±π且θ4≠±π时，此时式(3)中的系数A为零，且B、C、D、E均不为零时，将方程式(3)看作t4的一元二次方程，得到

(5)

其中

D2-4BC=16s12s34s41s23

式(5)可以分解时，需要t4的表达式可以写成有理分式的形式，需满足D2-4BC>0、BE=0，或D2-4BC=0、BE<0，可得

此时机构的运动学方程可因式分解。

然而，当球面4R机构结构参数仅使得式(3)中A为零，则BE、D2-4BC不为零。因而，此时式(3)不能写成两个有理分式相乘的形式，可知此时式(3)不能分解因式，当球面4R机构结构参数仅满足A为零，当θ1≠±π且θ4≠±π时，机构只具有一种变轴线转动运动模式。

现以结构参数使得式(3)中A为零的球面4R机构为例，对其运动模式进行分析。机构的结构参数α41=90°、α12=60°、α23=30°、α34=60°，该结构参数满足a12-a41+a34-a23=2kπ，且该机构结构参数不满足式(4)中的其他几个关系式，如图2球面4R机构3维模型所示。由图2d可知，当机构处于约束奇异位形时，其存在运动分岔的可能性，但当使得θ4随θ1变化的斜率不发生突变时，机构将通过该约束奇异位形且保持运动不发生分岔。

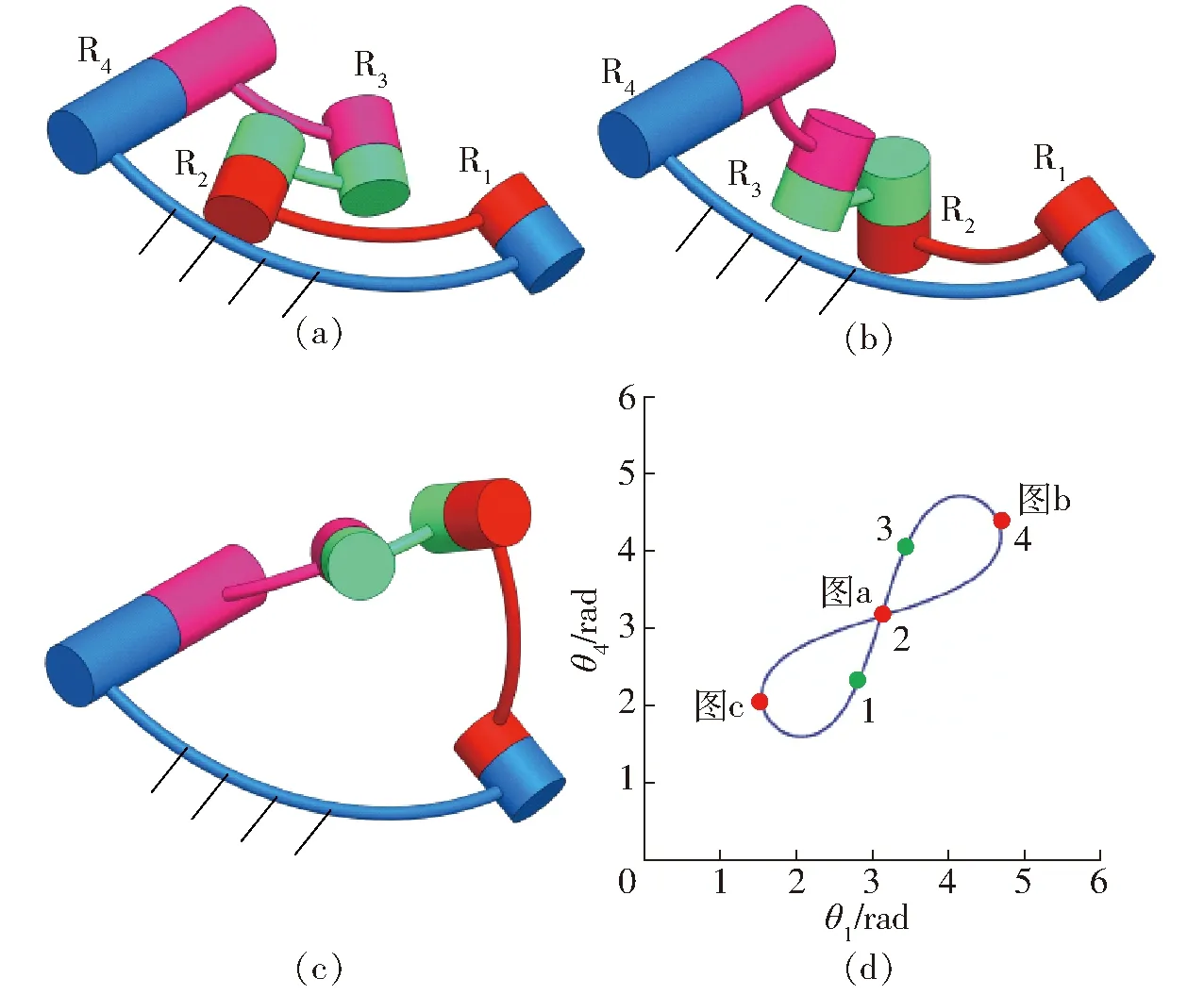
图2 球面1号4R机构位形Fig.2 Configuration of No.1 spherical 4R mechanism

当机构从图2d中点1机构位形，保持θ4随θ1变化的速率与点1、2、3所在曲线斜率相同时，该机构能动态通过点2对应的机构约束奇异位形，到达点3所对应的机构位形，即该机构可以通过点2处约束奇异位形而不发生运动分岔。实际上当机构速度不为零，从图2d点1对应位形运动到点2对应位形时，θ4随θ1变化的速率与点1、2所在曲线斜率相同。则当机构从点1所在机构位形运动到点2对应位形时，速度不为零时，即可通过点2所示约束奇异位形，且不发生运动分岔现象。同理，当机构从点3所示位形，运动到点4所示机构死点位形时，使得θ1的速度不为零时，机构可通过该死点位置。可以发现，在机构的点2对应的约束奇异位形和点4对应的死点位形下，机构均可动态通过，最终可到达所有的机构位形。

同理可知当式(3)中的系数B=0，或C=0，或E=0时，球面4R机构只具有1种变轴线转动运动模式，且结构参数满足这些条件的球面机构均与图2所示机构类似，机构可动态通过约束奇异位形，可运动到机构所有的位形。

3.2 球面4R机构运动模式(5号A=B=0)

当a12-a41+a34-a23=2kπ,a12+a41-a34-a23=2kπ，θ1=±π时，将机构结构参数代入式(2)，θ4为定值，此时机构不具有定轴转动模式。θ4=±π时，将机构的结构参数代入式(2)，整理得到恒等方程0=0。可知θ1可任意取值，机构具有一种以转动副R1为轴线的定轴转动运动模式。

当θ1≠±π,θ4≠±π时，A、B为零，C、D、E均不为零，整理式(3)得到的方程为二元二次方程。将该方程看作t1的一元二次方程，得到

(6)

其中

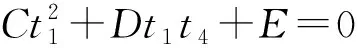
然而，当球面4R机构结构参数仅满足A、B为零时，CE、D均不为零，因而式(6)不能分解因式。从而，根据运动模式的定义可知，当球面4R机构结构参数仅满足A、B为零，当θ1≠±π,θ2≠±π时，连杆的瞬时轴线在随t1、t4不断变化，因而此时机构只具有一种变轴线运动模式。

现以结构参数使得式(3)中A、B为零的球面4R机构为例，对其运动模式进行分析。如图3球面4R机构的3维模型所示，机构的结构参数α41=90°，α12=45°，α23=45°，α34=90°，该结构参数满足式(4)中的关系式a12-a41+a34-a23=2kπ,a12+a41-a34-a23=2kπ。从图3d可知，当机构处于约束奇异位形时，其存在运动分岔的可能性，但当使得θ4随θ1变化的斜率不发生突变时，机构将通过该约束奇异位形且保持运动模式不发生改变。

当机构从图3d中点1机构位形(图3b)，保持θ4随θ1变化的变化率与点1、2所在曲线斜率相同时，该机构能动态通过点2对应的机构约束奇异位形(图3a)，但无法到达点3所对应的机构位形(图3c)，即该机构可以通过点2处约束奇异位形而不产生运动分岔。同理，当机构从图3d中点3机构位形，保持θ4随θ1变化的变化率与点2、3所在曲线斜率相同时，该机构能动态通过点2对应的机构约束奇异位形，但无法到达点1所对应的机构位形，即该机构可以动态通过点2处约束奇异位形而不发生运动模式改变。

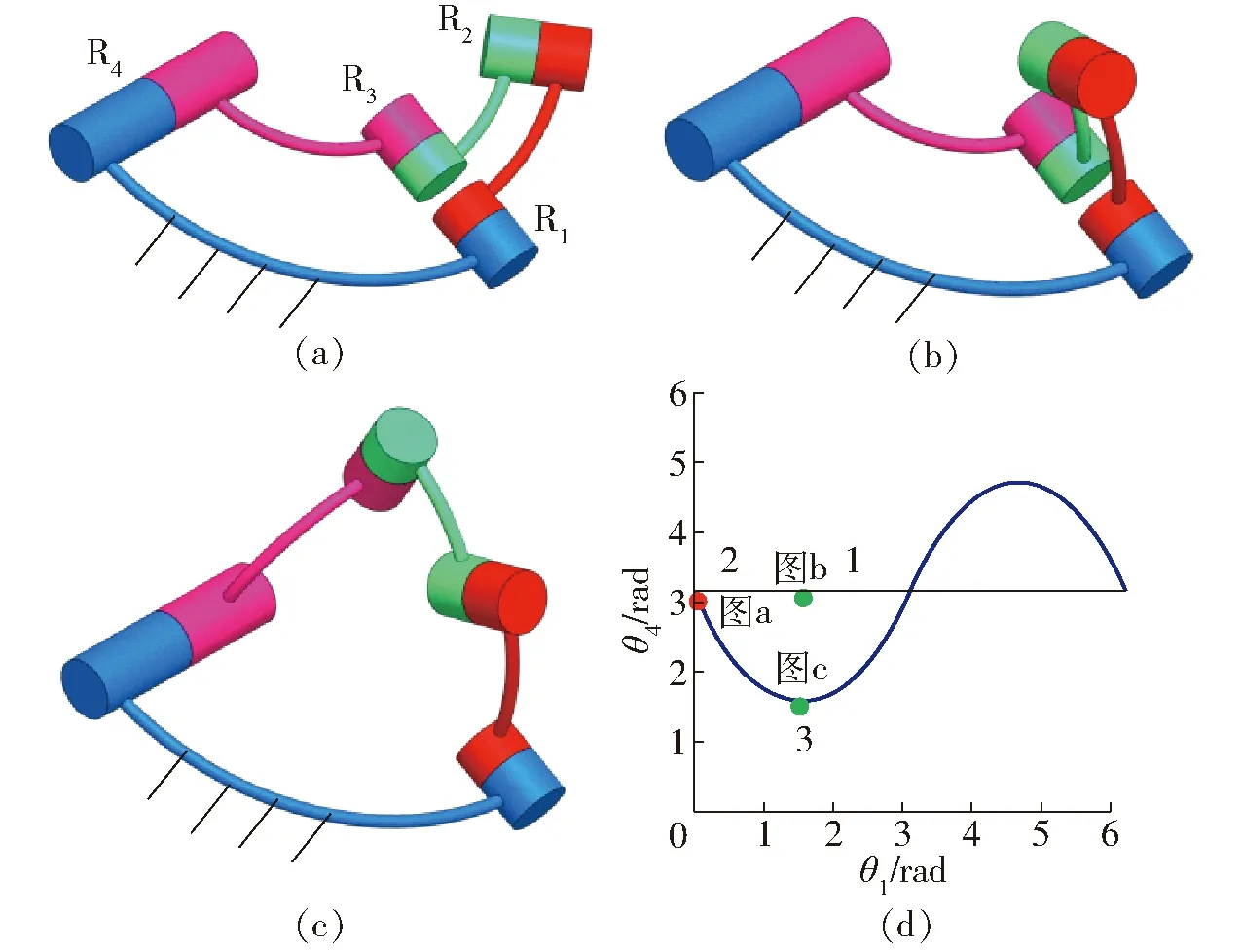
图3 球面5号4R机构位形Fig.3 Configuration of No.5 spherical 4R mechanism

从图3d可知，点1所对应的机构位形变换到点3所示机构位形时，通过在图3d点2所示位形时，θ4随θ1变化的变化率需要发生突变，从而实现机构运动模式的改变。一般情况下，使机构在运动中实现图3d所示两种运动模式的变换，十分的困难。可以使机构处于点2所示奇异位形时，保持机构静止不动，使得转动副R4和R1的转角速度为零，然后控制转动副R4与转动副R1转动实现机构运动模式的变换。

同理可知，当式(3)中的系数A=B=0，或A=C=0，或B=E=0，或C=E=0时，球面4R机构只具有1种定轴转动和1种变轴线转动共2种运动模式。

3.3 球面4R机构运动模式(8号B=C=0)

当a12+a41-a34-a23=2kπ,a12-a41-a34+a23=2kπ且θ1=±π或θ4=±π时，根据式(2)得到，θ4或θ1为定值，此时机构不具有固定轴线转动运动模式。

当θ1≠±π,θ4≠±π时，将8号球面机构结构参数代入式(3)整理得到B、C为零，A、D、E均不为零，得到的方程为二元四次方程，即

A(t1t4)2+Dt1t4+E=0

(7)

其中

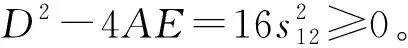
如图4球面4R机构的3维模型所示，机构结构参数α41=90°、α12=45°、α23=90°、α34=45°。该结构参数满足式(4)中的关系式a12+a41-a34-a23=2kπ,a12-a41-a34+a23=2kπ，如图4e所示，当机构处于约束奇异位形时，其存在运动分岔的可能性，但当使得θ4随θ1变化的斜率不发生突变时，机构将通过该约束奇异位形且保持运动不发生分岔。点3与点6所对应的机构位形相同，点1与点5所对应的机构位形相同。从图4e所示点1位形通过点2到达点3，通过点6到达点5机构位形，这整个运动过程属于第1种运动模式；从图4e所示点1位形通过点7到达点6，通过点3、4到达点5机构位形，这整个运动过程属于第2种运动模式。上述两种运动模式下，连杆的瞬时转动轴线均随转角θ1和θ4不断发生变化，即8号球面机构只具有两种变轴线转动运动模式。使机构处于奇异位形时，保持机构静止不动，使得转动副R4和R1的转角速度为零，然后控制转动副R4与转动副R1转动实现机构运动模式的变换。

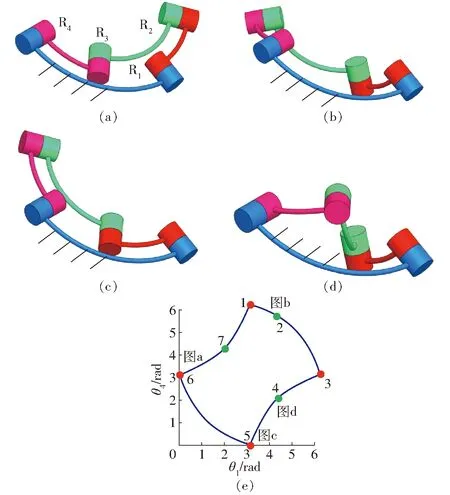
图4 球面8号4R机构位形Fig.4 Configuration of No.8 spherical 4R mechanism

同理可知，当式(3)中的系数B=C=0时，球面4R机构只具有2种变轴线转动运动模式。

3.4 球面4R机构运动模式(14号B=C=E=0)

当a12+a41-a34-a23=2kπ,a12-a41-a34+a23=2kπ,a12+a41+a34+a23=2kπ，且θ1=±π或θ4=±π时，根据式(2)得到，θ4或θ1为定值，此时机构不具有固定轴线转动运动模式。

当θ1≠±π,θ4≠±π时，将14号球面机构结构参数代入式(3)整理得到B、C、E为零，A、D均不为零，得到的方程为二元四次方程

t1t4(At1t4+D)=0

(8)

当球面4R机构结构参数仅满足B、C、E为零，A、D均不为零，该式可以分解因式。从而，根据运动模式的定义可知，当球面4R机构结构参数仅满足B、C、E为零，球面4R机构恒具有3种运动模式。两种为定轴转动模式，一种为变转动轴线转动模式。

如图5所示，球面4R机构的3维模型机构的结构参数α41=120°、α12=60°、α23=120°、α34=60°。该结构参数满足式(4)中的关系式，a12-a41+a34-a23=2kπ，a12-a41-a34+a23=2kπ,a12+a41+a34+a23=2kπ。

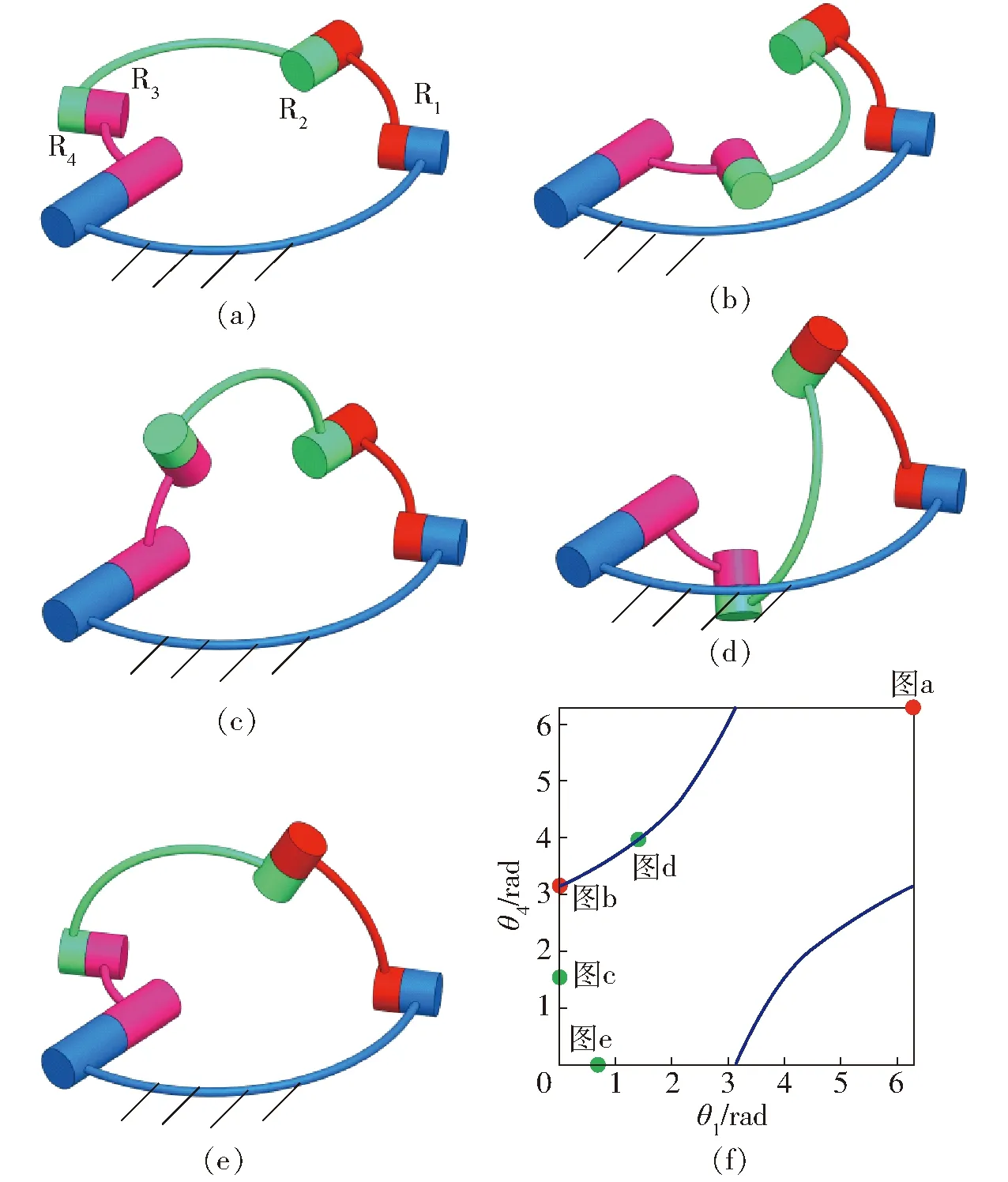
图5 球面14号4R机构位形Fig.5 Configuration of No.14 spherical 4R mechanism

如图5f所示，当机构处于约束奇异位形时，其存在运动分岔的可能性，但当使得θ4随θ1变化的斜率不发生突变时，机构将通过该约束奇异位形且保持运动模式不发生改变。使机构处于奇异位形时，保持机构静止不动，使得转动副R4和R1的转角速度为零，然后控制转动副R4与转动副R1转动实现机构运动模式的变换。

同理可知，当式(3)中的系数A=B=C=0,或A=B=E=0,或A=C=E时，球面4R机构只具有2种定轴线转动和1种变轴线转动共3种运动模式。

3.5 球面4R机构运动模式(15号A=B=C=E=0)

将15号球面4R机构结构参数代入式(2)，当θ1=±π时，得到0=0，即该式恒成立。即转动副R1的转角θ1为±π时，转动副R4的转角θ4可自由转动，此时对应球面4R机构连杆可以绕转动副R4的轴线做定轴转动。当θ4=±π时，将该式整理得到0=0，即该式恒成立。即转动副R4的转角θ4为±π时，转动副R1的转角θ1可自由转动，此时对应球面4R机构连杆可以绕转动副R1的轴线做定轴转动。

当θ1≠±π,θ4≠±π时，将15号球面机构结构参数代入式(3)整理得到A、B、C、E为零，D不为零，得到二元二次方程

t1t4=0

(9)

当球面4R机构结构参数仅满足A、B、C、E为零，D不为零，该式可以分解因式。即t1=0对应转动副R1的转角θ1为0时，转动副R4的转角θ4可自由转动，此时对应球面4R机构连杆可以绕转动副R4的轴线做定轴转动。t4=0对应转动副R4的转角θ4为0时，转动副R1的转角θ1可自由转动，此时对应球面4R机构连杆可以绕转动副R1的轴线做定轴转动。

从而可知，当球面4R机构结构参数仅满足A、B、C、E为零，球面4R机构恒具有4种定轴转动运动模式。

如图6球面4R机构的3维模型所示，机构的结构参数α41=90°、α12=90°、α23=90°、α34=90°，其结构参数满足式(4)。从图6g可知，当机构处于约束奇异位形时，其存在运动分岔的可能性，但当使得θ4随θ1变化的斜率不发生突变时，机构将通过该约束奇异位形且保持运动模式不发生改变。使机构处于奇异位形时，保持机构静止不动，使得转动副R4和R1的角速度为零，然后控制转动副R4与转动副R1转动实现机构运动模式的变换。

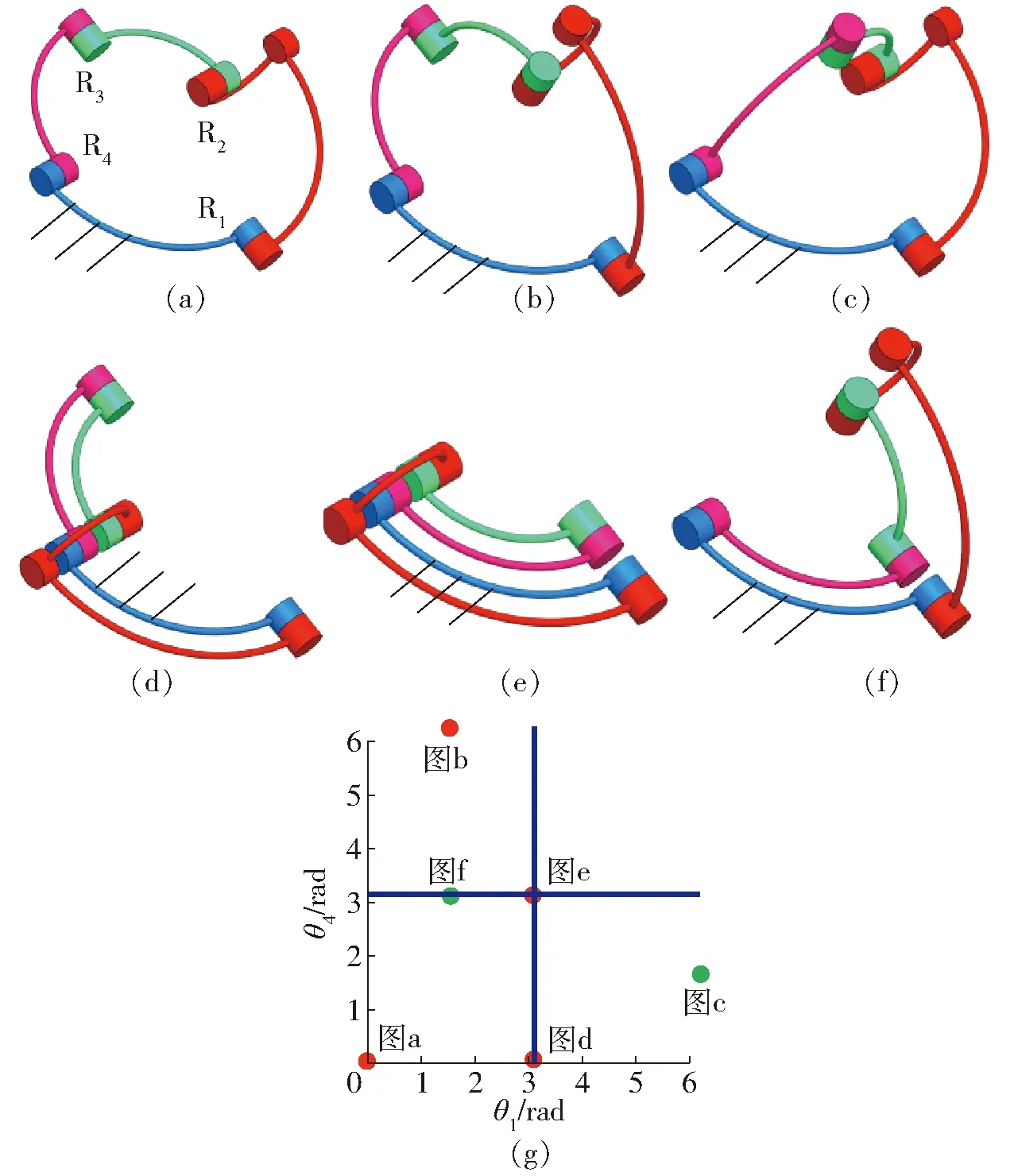
图6 球面15号4R机构位形Fig.6 Configuration of No.15 spherical 4R mechanism

综上所述，可将式(3)的多项式系数A、B、C、E分别置零，进行组合后，得到的结构参数关系式，可设计具有不同运动模式特征的球面4R机构。这类球面4R机构所具有的运动模式如表1所示。表1中Sm为机构运动模式数目，Sf为球面4R机构固定轴线转动运动模式数目，Sv为球面4R机构变轴线运动模式数目。

表1 具有约束奇异位形的球面4R机构运动模式数目Tab.1 Motion mode of spherical 4R mechanism with constrained singular configuration

根据表1可知，1～4号机构只具有1种变轴线转动运动模式；5、6、9、10号机构只具有1种定轴线和1种变轴线共2种转动运动模式；7、8号机构具有2种变轴线共2种转动运动模式，11～14号机构具有1种变轴线、2种定轴线3种转动运动模式；15号机构具有4种定轴线转动运动模式。

4 球面4R机构约束奇异位形瞬时转动轴线

建立如图7所示的球面4R机构坐标系，当机构的4个转动副轴线在XOY平面内，相交于点O。转动副R4的轴线与向量OA重合，转动副R1的轴线与向量OB重合。转动副R1、R2轴线所在平面Σ12与转动副R4、R3轴线所在平面Σ43的交线与OC重合，转动副R4绕向量OA转动有限角度θ4后，转动副R1转动有限角度θ1，转动副R4、R3轴线所在平面OAC的法线沿Z轴方向，绕转轴R4转动π-θ4；转动副R1、R2轴线所在平面OBC的法线沿Z轴方向，绕转轴R1转动θ1。

图7 球面4R机构连杆瞬时轴线几何关系Fig.7 Geometric relationship of instantaneous axis of connecting rod of spherical 4R mechanism

平面OAC的法线在OXYZ坐标系中为

(10)

平面OBC的法线在OXYZ坐标系中为

(11)

平面OAC、OBC法线的共垂线平行于向量

(12)

式(12)可写成形式

(13)

式(12)为球面4R机构连杆的瞬时转动轴线的方向向量。当球面4R机构趋近于奇异位形时，式(12)的极限值即为球面4R机构趋近于奇异位形时连杆的瞬时转动轴线。当球面4R机构趋近于奇异位形时c1/c4=±1。因而，约束奇异位形下连杆瞬时转动轴线方向向量式(13)的极限值为

(14)

式(14)可通过几何方法进行验证。如图7所示OA与转动副R4的轴线重合，OB与转动副R1的轴线重合。CA为转动副R4、R3所在平面Σ43的直线，CB为转动副R1、R2所在平面Σ12的直线。OC即为上述两平面的交线，即球面4R机构连杆的瞬时转动轴线。点A、B均在平面OXY上，点C在平面OXY上的投影为点D，DA垂直于OA，BD垂直于OB。由于CD垂直于AD、CD垂直于OA，且AD垂直于OA，因而根据转动副R4的转角θ4得出∠CAD为π-θ4。同理，根据转动副R1的转角θ1得出∠CBD为π-θ1。

根据图7的几何关系，可得到

(15)

(16)

(17)

根据式(15)～(17)可得到

(18)

球面4R机构在运动分岔时分3种情况，第1种，两分岔轨迹均为变轴线运动模式。第2种，两分岔轨迹均为定轴线运动模式。第3种，两分岔轨迹中一个为定轴线运动模式，另外一个为变轴线运动模式；计算分岔运动轨迹在机构位形趋近于约束奇异位形时s4/s1的值。结合上述3种情况由式(14)可知，表1中球面4R机构在趋近于约束奇异位形时，不同分岔运动轨迹连杆的瞬时转动轴线均不重合。