含折展平台的多模式移动并联机构设计与运动特性分析

2022-04-07张春燕

农业机械学报 2022年3期

张春燕平安

(上海工程技术大学机械与汽车工程学院，上海 201620)

0 引言

农业机器人备受学者的广泛关注，尤其是适用于特殊复杂地形作业的农业机器人[1-3]。由于丘陵山地土层松软，具有陡坡、岩石等复杂地形环境，传统轮式、足式和履带式农业机器人很难适应这种环境的作业任务[4]。因此，对丘陵山地等农业环境的农业机器人提出了空间小型化与移动多样性的高要求。随着机器人技术的迅速发展，具有一定可变形[5]、自重构[6]、多操作模式[7-8]的多模式移动机构逐渐成为机器人在农业领域应用的研究热点。张硕等[9]提出一种形态重构，以适应农业复杂环境的移动机器人。AZIMI等[10]研究用于温室环境的农业移动机器人。FOUNTAS等[11]研究针对田间作业的农业移动机器人。ZHANG等[12]提出具有滚动与自穿越特性的3-RSR自变形多模式移动并联机构。LIU等[13]基于单环运动链提出四杆移动机器人。上述这些移动机器人可通过自变形、可重构等方式在复杂环境实现自我重组从而实现越障与移动；但因机器人不具备较强折展能力，导致整体结构与普通移动机器人相比较为庞大[14]，不便于携带和无法适应丘陵山地的复杂地形环境。

而折展机构因具有占用体积小，折叠收纳能力强等优点被应用于工程、小范围作业等机器人领域[15-20]。因此，本文运用“折展”理念将具有较大空间折展能力的8R结构[21]应用到适应丘陵山地作业机构设计中。利用折展8R机构的分岔位置特性[22-23]具有自由度可变的特点，实现机构在丘陵山地作业中折展与各运动模式间切换等功能，并根据螺旋理论[24]与图论[25]对机构在各运动模式下的自由度和切换机理进行分析，同时采用ZMP[26]原理分析机构移动模式的运动特性，在ADAMS软件中进行仿真，最后通过设计样机验证机构设计的可行性。

1 机构平台设计

1.1 折展平台结构设计

8R具有运动分岔特点，可通过改变转动副轴线关系实现机构的运动位型转换[21]。本文即借助这一原理设计移动并联机构的折展平台，如图1a所示，折展平台由8个R副和8根长度相同的杆件首尾相连组成。定义机构的分岔位型为折展平台的初始位形，如图1b所示，此时轴线旋量$i(i=1,3,5,7)相互平行，旋量$i(i=2,4,6,8)交于一点Q，折展平台处于完全展开位型；改变平台轴线位置如图1所示，当旋量$i(i=1,3,5,7)交于一点P，旋量$i(i=2,4,6,8)交于一点Q时平台处于另一分岔过渡位型，可以实现前后位型的过渡变换；继续改变轴线位型如图1c所示，旋量$i(i=1,3,5,7)交于一点P，旋量$i(i=2,4,6,8)交于一点Q，此时，两组旋量分别共线、正交形成的平面相互平行，且P投影与Q重合，平台此时处于完全折叠位型。

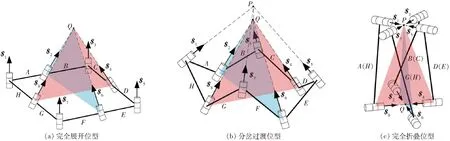
图1 折展平台各轴线位置Fig.1 Position of each axis of folding platform

为实现图1所示折展平台的3种位型，连接8个R副的杆件应设计成如图2a所示的形状，杆长为l，杆的截面如图2b所示，转动副轴线半径为r，竖直的轴线与杆件截面围成一个边长为a的正方形；且为确保8根杆件可首尾相连，位于每根杆首尾位置的两个R副轴线空间呈角度λ。

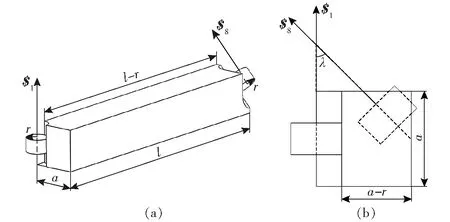
图2 折展平台连杆设计图Fig.2 Platform linkage design

依照相邻两转动副轴线方向相同的原则，将8根杆通过转动副R进行铰接，相邻连杆之间的夹角为φ，构成如图3所示的折展平台，分别对应图1所示的各轴线位型。

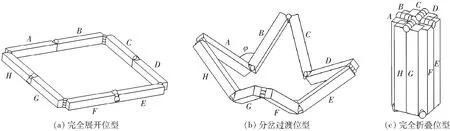
图3 折展平台各位型Fig.3 Each type of folding platform

1.2 折展平台折展性

当平台由完全展开的初始位型向完全折叠状态切换时，如图3c所示，会发现由于杆截面形状的影响，相邻两根杆在完全折叠时出现干涉。以图3中杆A和H为例，在折叠时杆件会发生如图4a所示的重叠干涉，为消除这种干涉需对平台连杆截面进行截面优化(图4b)，从截面起始沿杆件方向切除c，切除后截面直角端与底面间的夹角为λ′。

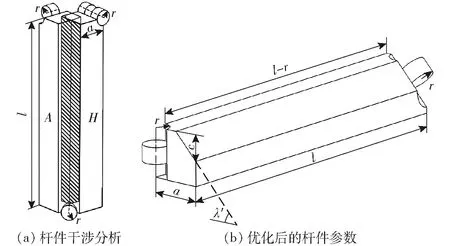
图4 平台连杆干涉分析与优化Fig.4 Interference analysis and optimization of platform linkage

在折展过程中，由于平台连杆截面切除量c与平台连杆长宽比参数不同，使机构折展率受到的影响不同，故对平台连杆截面的切除量c和平台连杆长宽比k(k=l/a)进行分析。根据几何关系得折展位型下折展率η计算式为

(1)

式中sD——平台完全展开面积

sF——平台完全折叠面积

通过图3c可得，为使平台可以完全折叠，截面需要对称切除，则λ′=45°。由此根据式(1)可得机构折展率η随切除量c和长宽比k的变化图谱。由图5可看出，机构折展率随切除量c和长宽比k的增加而增大。当切除量c=40 mm、长宽比k=6时，平台折展率达到最大，此时c与k为平台最优参数。平台折展位型如图6所示，从图6可以看出，平台展开没有影响(图6a)，且完全折叠没有发生干涉(图6b)，平台杆件参数设计合理。

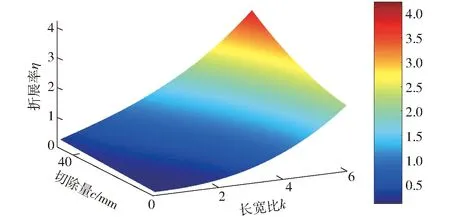
图5 折展率变化曲面Fig.5 Variation curve of folding and deploying rate

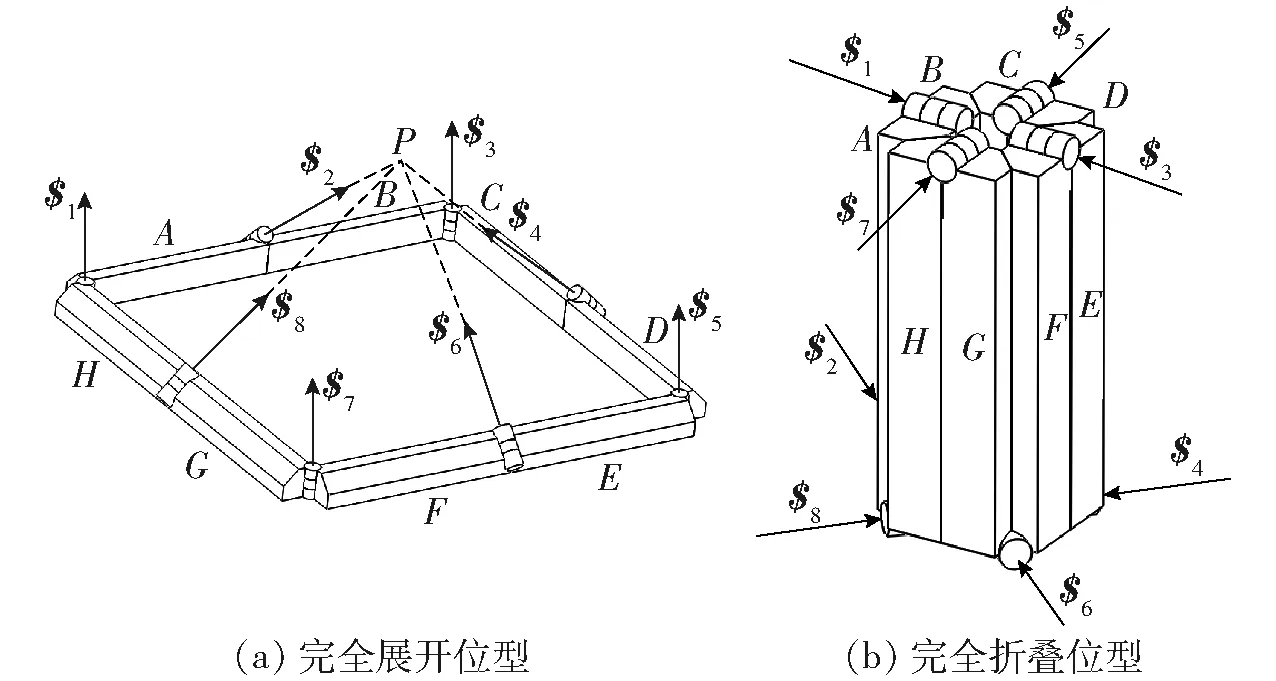
图6 优化设计后折展平台Fig.6 Optimized design of folding platform

2 可折展移动并联机构多模式切换机理

2.1 多模式折展机构设计

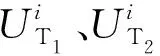
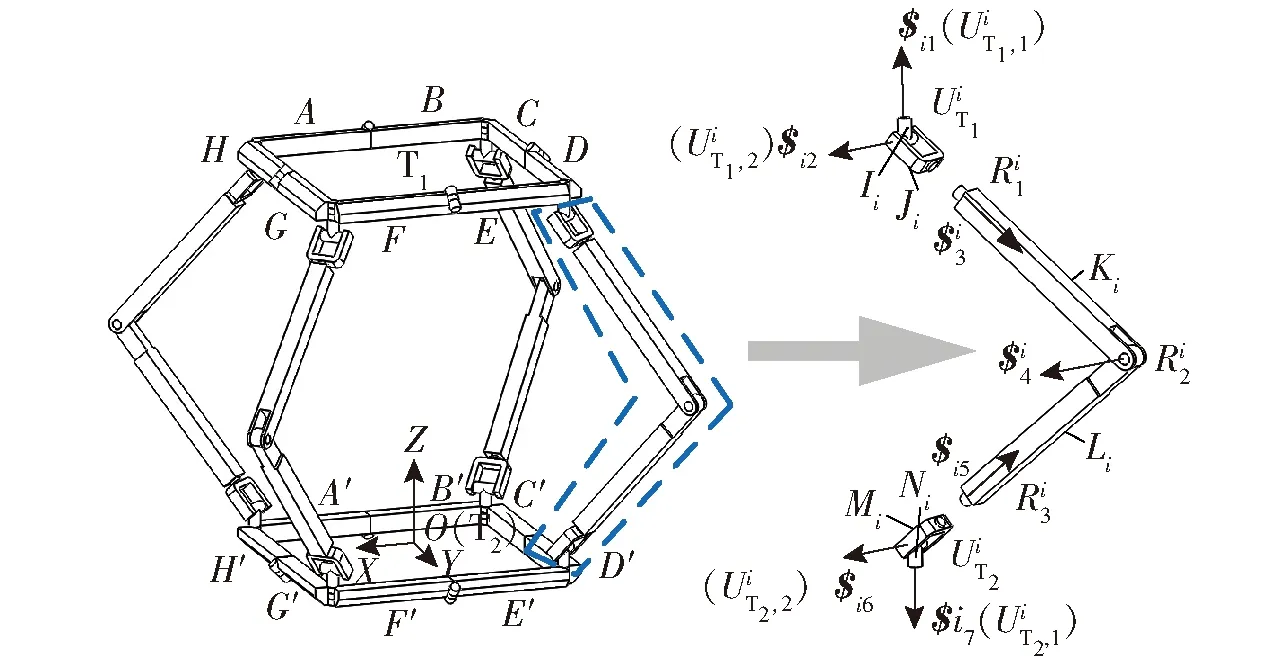
图7 可折展多模式并联机构与支链示意图Fig.7 Schematic of foldable multi-mode parallel mechanism and branch chain

2.2 可折展并联机构多运动模式及自由度分析

2.2.1可折展并联机构各运动模式分析

旋量的变化会使机构自由度发生改变，从而导致机构模式的切换[27]。因此当图1平台轴线的分岔位形发生变化使可折展并联机构自由度发生改变而具有多种模式。图8a为机构移动状态旋量图，此时平台T1旋量$2、$4、$6、$8存在交点Q,平台T2旋量$10、$12、$14、$16存在交点Q′，此时平台T1旋量$1、$3、$5、$7和平台T2旋量$9、$11、$13、$15均不存在交点。而当平台转动副转动到图8所示机构折展状态时，Q、Q′点仍存在，折展平台T1旋量$′1、$3、$5、$7交于一点P,平台T2旋量$9、$11、$13、$15交于一点P′，机构自由度发生改变，使机构

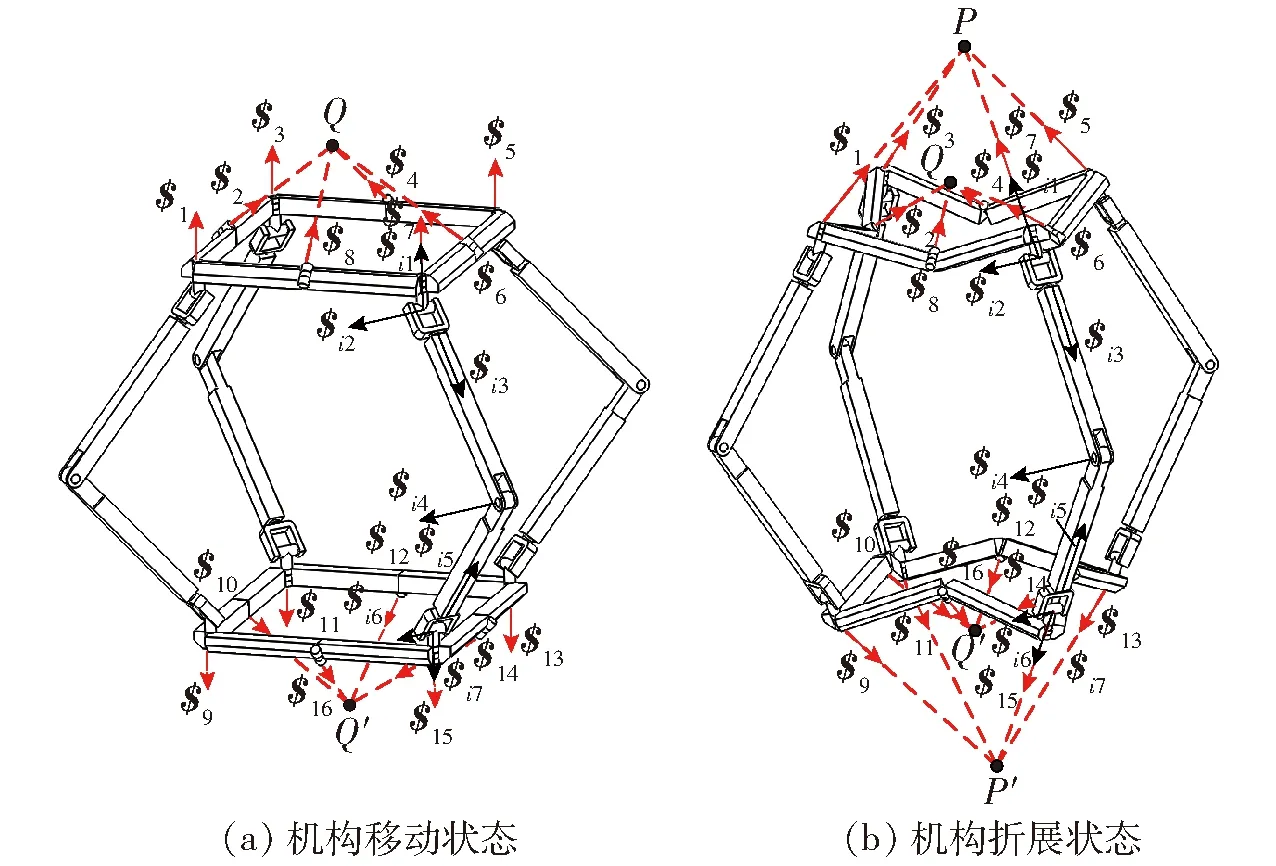
图8 机构旋量图Fig.8 Screw diagrams of mechanism

从移动模式切换到折叠模式，机构具体切换过程如图9所示。

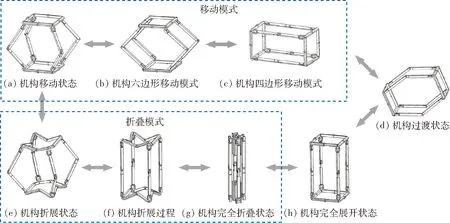
图9 可折展机构的多种运动模式Fig.9 Multiple modes of mechanism

2.2.2可折展并联机构各运动模式下自由度

自由度是机构实现运动的依据，文献[28-29]中基于图论和螺旋理论对机构自由度进行计算和分析，可以对机构旋量组成进行描述，具有结构表达清晰、易于数学求解等优点。通过绘制机构不同状态下的旋量约束拓扑图，将旋量约束方程组转换为旋量约束矩阵并计算出矩阵零空间维数，矩阵零空间维数等于矩阵列数减去秩数即为机构自由度。这种计算自由度的方式比单纯用旋量理论从支链开始求

解更能考虑可变平台对机构自由度的影响。

如图9a、9b分别为机构移动模式与折叠模式的起始状态，这两种状态的改变直接导致机构从移动模式切换到折叠模式，故以这两种状态为例，计算机构自由度并解释了移动模式向折叠模式的切换原理。

如图10所示带字母与标号的圆圈代表构件，线条表示各构件间运动副，运动旋量代表关节处运动副的运动，依据图9a所示机构移动状态依次绘制闭环旋量约束拓扑图。根据闭环矢量法，发现机构在这种运动状态可以形成Ⅰ～Ⅴ共5个闭环，其中上平台闭环用Ⅰ表示，下平台闭环用Ⅱ表示；而支链与平台及相邻支链间均可形成闭环。

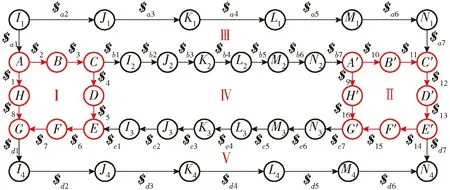
图10 机构移动状态闭环旋量约束拓扑图Fig.10 Screw constraint topology graph of moving state

用ωij(i=a,b,c，d;j=1,2,…,16)表示平台旋量$i(i=1,2,…,16)与支链旋量$ij(i=a,b,c,d；j=1,2,…,7)对应转动副的角速度，根据图10中的Ⅰ～Ⅴ共5个闭环，建立机构移动状态旋量约束方程组为

(2)

将式(2)写成矩阵的形式

MN=O

(3)

其中

(4)

(5)

(6)

旋量约束矩阵M为一个30×44维矩阵，机构移动状态自由度对应于旋量约束矩阵的零空间维数，通过计算可得

rank(M)=41

(7)

旋量约束矩阵M的列数为44，其零空间的维数为列数减去矩阵的秩数，可得机构移动状态所代表的移动模式自由度为3。

机构从图9a移动状态变化到图9e折展状态的旋量约束拓扑图如图11所示,其中平台T1运动旋量$1～$8与平台T2运动旋量$9～$16发生改变，旋量约束拓扑图中对应改变运动旋量的箭头变成虚线表示，旋量约束拓扑图改变使建立的约束方程组和矩阵也发生改变并影响自由度计算结果。

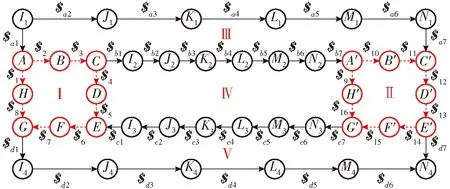
图11 机构折展状态闭环旋量约束拓扑图Fig.11 Screw constraint topology graph of folding state

式(2)中的$1～$16发生改变，点P、P′满足形成条件矩阵M中M2～M13发生改变,改变后矩阵M′为一个30×44维矩阵，代入式(3)得

rank(M′)=42

(8)

机构折展状态自由度为旋量约束矩阵的零空间维数，旋量约束矩阵M′的列数为44，零空间的维数为列数减去秩数，得到折展状态机构自由度为2。

同理，将图9b六边形移动模式与图9c四边形移动模式下根据旋量约束拓扑图改变后的各旋量代入相应的矩阵中，可以分别得到机构在六边形移动模式下的自由度为3，在四边形移动模式下的自由度为1。

3 可折展机构各运动模式电机驱动实现

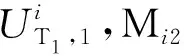
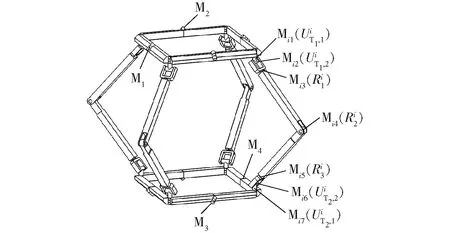
图12 机构电机分布示意图Fig.12 Motor distribution of mechanism

依据文献[13]将电机状态分为驱动(●)、锁定(○)、失效(⊗)3种不同状态，通过改变电机状态使机构发生运动变形，改变平台点P(P′)存在条件，使机构自由度数改变切换不同运动模式。机构在实现不同运动模式时，机构所处运动状态、点P(P′)是否存在、自由度、电机状态如表1所示。

表1 机构不同模式下自由度与电机状态Tab.1 Number of degrees of freedom and state of motor in different modes

4 移动模式运动特性分析

本文所研究的可折叠多模式移动并联机构，主要工作状态是移动模式，机构实现移动运动时不仅要满足自由度与电机驱动条件，还要考虑移动过程中的稳定特性，分析计算机构在滚动过程中驱动角度对质心变化的影响，为ADAMS仿真提供运动参数。

4.1 六边形移动模式运动稳定性

机构在六边形移动模式下运动方式为六边形滚动，质心ZMP分析为机构能否实现稳定滚动与驱动输入提供判断与选择依据，如图13所示，六边形滚动时分别由2条支链与上下平台的连杆组成2个运动状态完全相同的6R闭环，因此计算重心的位置时相对应位置运动完全相同的连杆可以当成一个整体进行分析。根据以上运动学分析可得机构输入角θ1、θ2、θ3与ZMP变化关系为

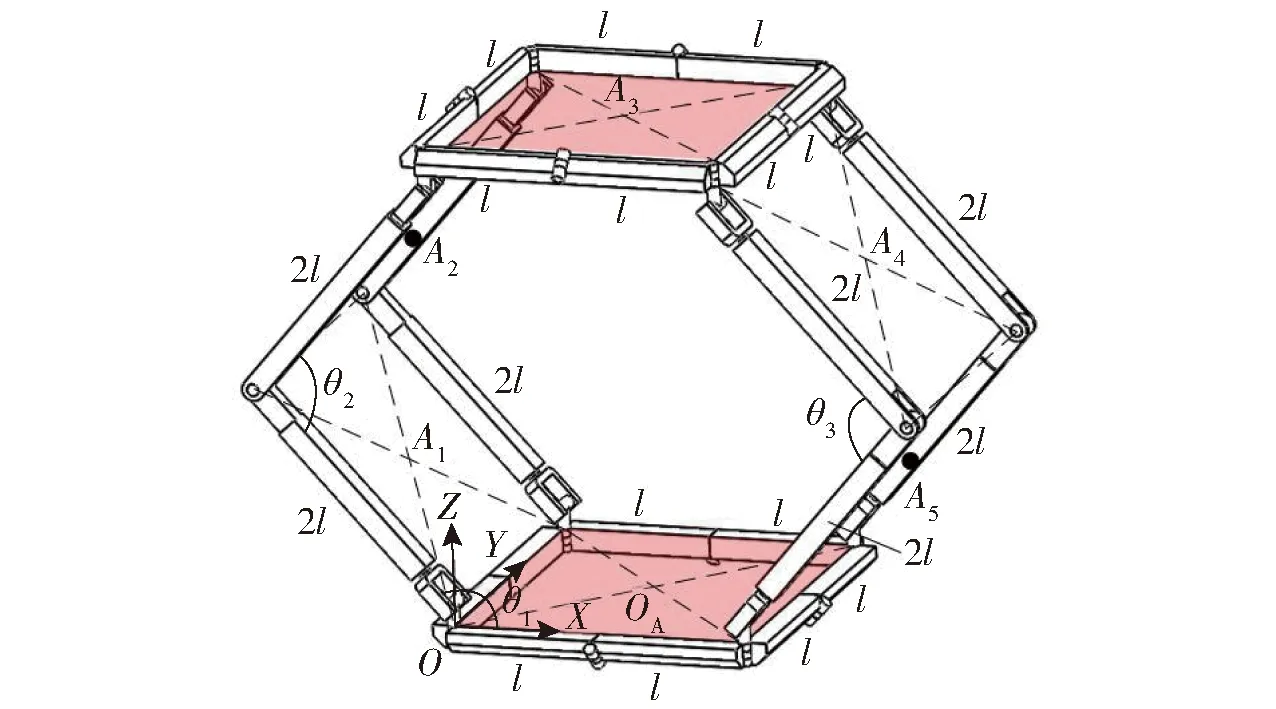
图13 六边形移动模式坐标系Fig.13 Coordinate system diagram of hexagonal movement mode

(9)

(10)

式中mi——第i杆件质量

Ji——第i杆件转动惯量

αi——第i杆件角加速度

g——重力加速度

xi、yi、zi——第i杆件的质心坐标

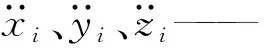
各个连杆的质量均为m，此时由下平台与地面接触，支撑区域中心位置坐标OA(l,l,0)，由几何关系可知各滚动平面质心A1～A5以及以上所求角度，分别代入式(9)、(10)可以得到输入角θ1、θ2与ZMP的关系如图14所示。

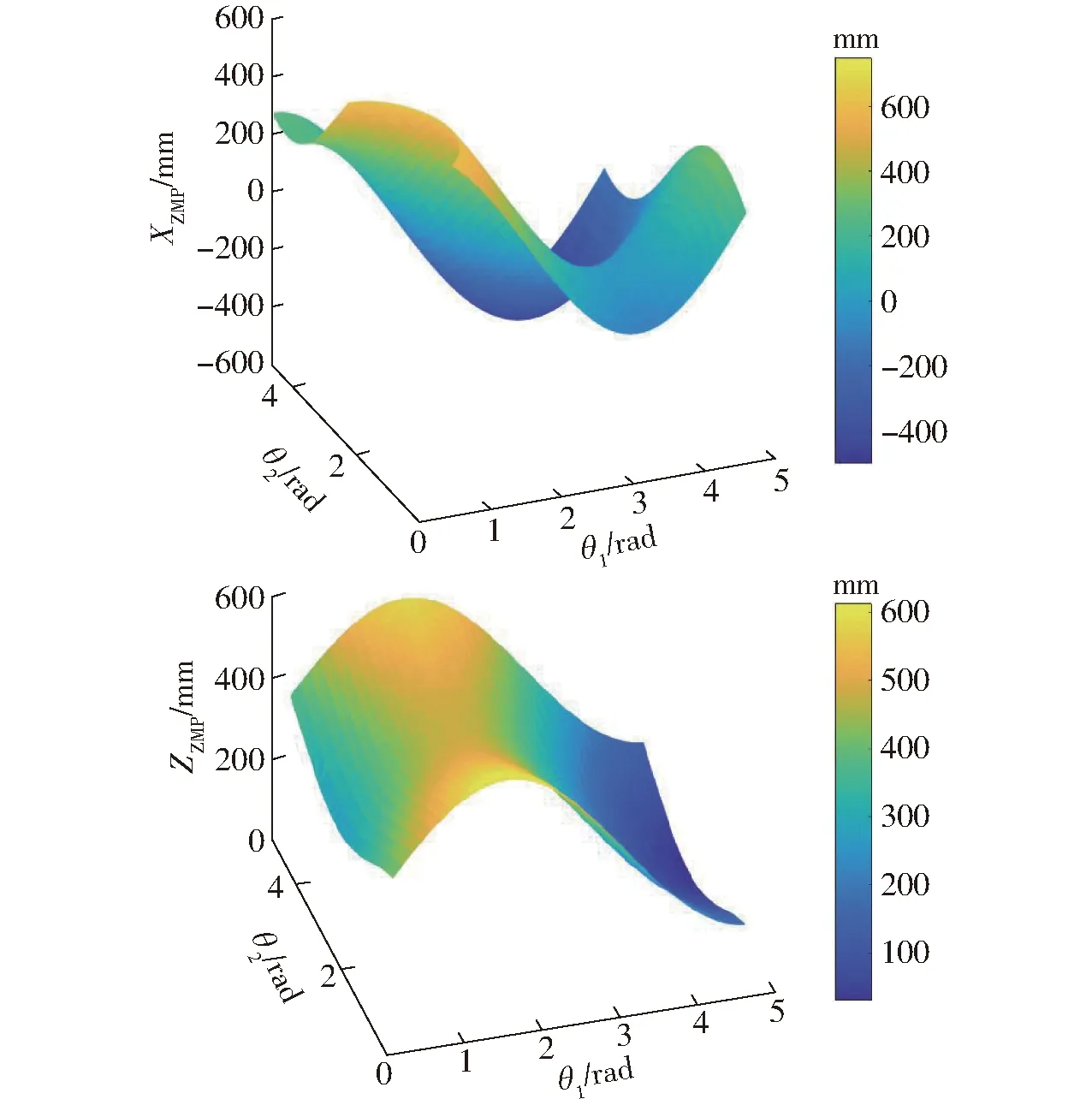
图14 XZMP、ZZMP随角度的变化曲面Fig.14 ZMP of X axis and Z axis change with angle graph

由图14可知，0<θ1<2 rad、0<θ2<3 rad时，XZMP>0、ZZMP>0时机构六边形移动模式滚动处于稳定状态。2 rad<θ1<5 rad、3 rad<θ2<5 rad时，XZMP<0、ZZMP>0时机构六边形移动模式滚动处于失稳状态，即此时机构处于倾翻过程。

4.2 四边形移动模式运动稳定性

机构在四边形移动模式下运动方式为四边形滚动，其坐标系及边长参数如图15所示，假设机构中所有的杆件质量均匀分布且质心位于其几何中心处，连杆质量为m1，支链质量为m2，此时上下平台的两条连杆及两条支链与地面接触。代入式(9)、(10)，可得输入角θ与ZMP的关系如图16所示。

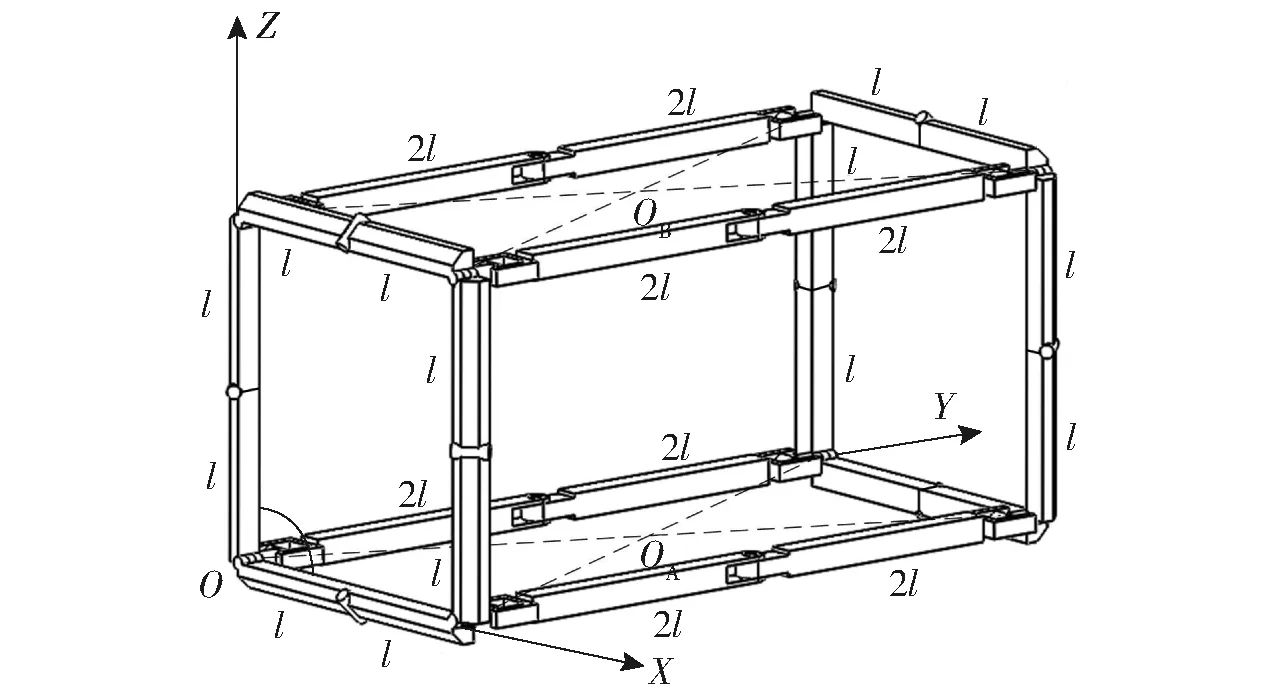
图15 四边形移动模式坐标系Fig.15 Coordinate system diagram of quadrilateral movement mode

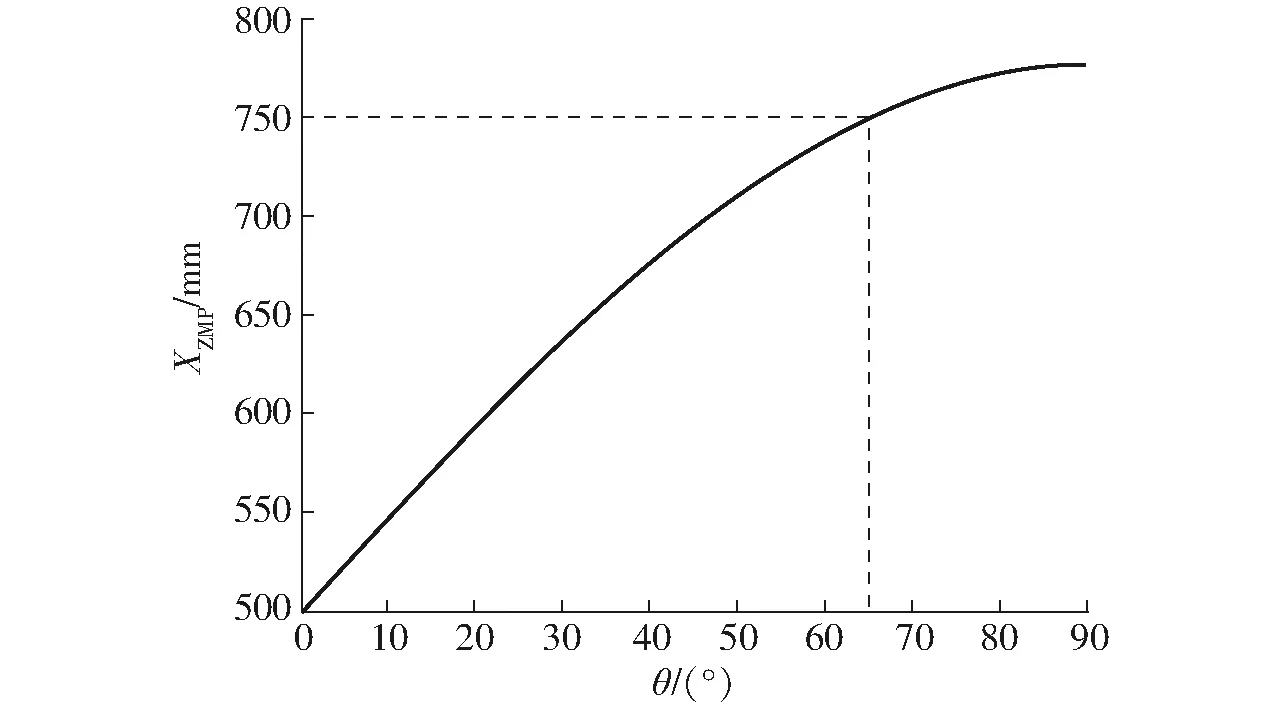
图16 XZMP随输入角θ的变化曲线Fig.16 ZMP of X axis change with angle graph

由图16可知，当θ达65°时，ZMP在X轴方向上达到机构稳定支撑的极限位置，0°<θ<65°时机构四边形移动模式滚动处于稳定状态，65°<θ<90°时机构四边形移动模式滚动处于失稳状态，即此时机构处于倾翻过程。

5 机构各运动模式仿真

为验证折展平台设计在机构中的合理性，建立机构虚拟样机模型，其基本参数为：平台连杆长度95 mm；支链连杆长度190 mm；所有驱动转动副速度为0.28 rad/s，对机构进行ADAMS仿真验证。

5.1 折叠模式

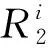
图17 折叠模式仿真Fig.17 Folding mode simulation

5.2 六边形移动模式

对机构六边形移动模式进行仿真，一个运动周期内位置随时间改变如图18所示。支链上安装电机Mi1发生转动使得4条支链中同侧支链形成的平面平行于移动方向，如图18a所示；通过4条支链上电机M16转动，整个机构姿态发生变化运动到图18b；电机M12、M16、M44协同转动使机构运动到图18c；通过电机M12、M16转动使机构运动到图18d。支链电机M44转动使机构运动到图18e；通过电机M12、M16、M44协同转动使机构运动到初始位置，如图18f。

图18 六边形移动模式仿真Fig.18 Hexagonal movement mode simulation

5.3 四边形移动模式

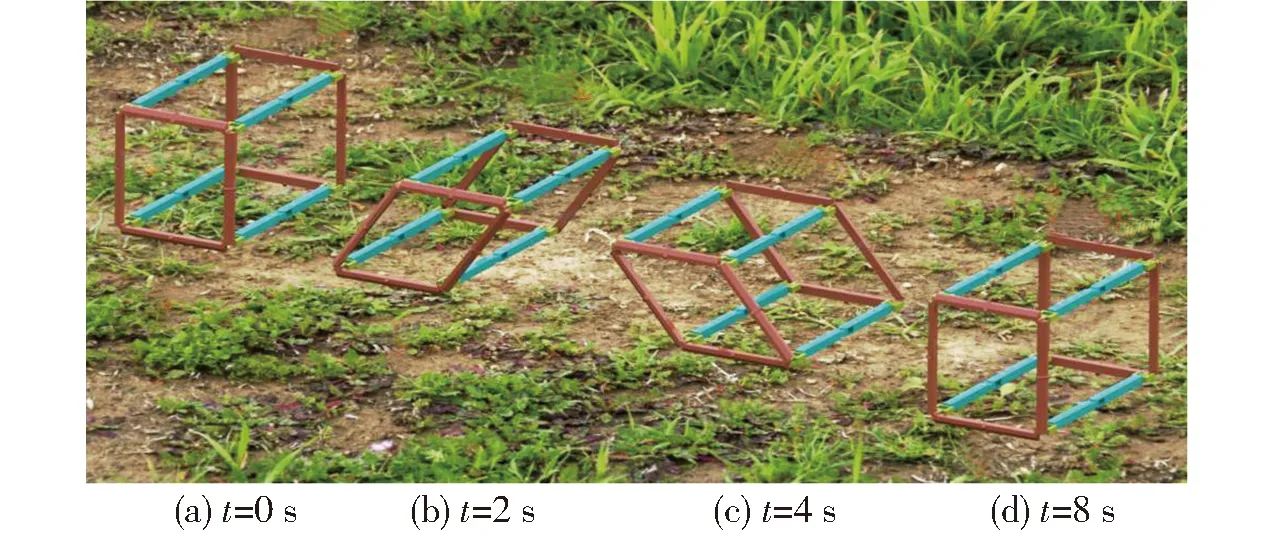
图19 四边形移动模式仿真Fig.19 Quadrilateral movement mode simulation

6 样机试验

根据理论分析及仿真结果，为验证机构设计的合理性，对含折展平台的多模式移动并联机构进行工程设计并制作原理样机，如图20所示。样机参数为样机长230 mm、宽230 mm、高430 mm、总质量2.4 kg、平台材料为工程塑料、杆件材料为碳纤维、电机型号为ToworPro MG996R、控制板为STM2、工作电压为7.2 V。