基于PSO-DBSCAN和SCGAN的未知雷达信号处理方法

曹鹏宇, 杨承志, 石礼盟, 吴宏超

(1. 空军航空大学航空作战勤务学院, 吉林 长春 130022; 2. 中国人民解放军93671部队, 河南 南阳 474350)

0 引 言

作为感知电磁态势的重要方法,雷达侦察技术在电子战中发挥着举足轻重的作用。随着电磁环境日益复杂,传统基于脉间参数的分选识别算法性能难以满足现代军事需求。雷达信号的单脉冲内部参数又被称为脉内参数,与脉间参数相比包含了更为丰富的特征,对单脉冲进行识别是当前雷达侦察领域研究的重点。

随着深度学习在计算机视觉、自然语言处理等领域的广泛应用,不少专家学者将深度学习应用于雷达信号分类识别领域。文献[21]提出一种基于数据场理论联合脉冲重复间隔与聚类的雷达信号分选方法。文献[22]提出一种基于时序相关和聚类的重点雷达信号实时识别方法。文献[23]提出一种在小样本条件下对雷达目标的识别方法。文献[24]提出一种基于时频分析和扩张残差网络的雷达辐射源信号自动识别方法。上述方法都是基于已知信号或者未知信号的识别问题,未考虑到实际战场环境下,雷达侦收到的信号是样本库中已知信号和大量未知信号的混合信号。上述方法难以解决此种情形。

本课题组成员在文献[25]中提出了基于一维残差和三元组损失函数的雷达信号的识别方法。使用一维残差网络提取特征,三元组损失函数对网络进行训练。训练完成后,通过度量输入信号与数据库中已知类别的信号的相似性,以最近邻的方式实现了已知雷达信号的型号识别。当输入为未知信号时该方法判断其并非为样本库中的型号,将信号标签设置为-1后存储在未知雷达库中,但并没有对未知信号进行后续处理。

因此,本文结合文献[25]中已知信号分类识别算法的原理,分析了未知雷达信号处理过程中需要解决的问题如下:

(1) 未知信号中包含的雷达型号数量未知,划分聚类方法需预先设置簇的数量,并不适合解决此问题。层次聚类和密度聚类方法虽然不需要预先设置簇的数量,但层次聚类计算复杂度非常大且易受奇异值影响,密度聚类在计算量上要求不如层次聚类,但对输入参数设置敏感;

(2) 聚类算法准确率相对较低,聚类后得到的各个簇中包含部分不属于该簇的错误个体。全部扩充到雷达库中会造成分类可信度下降;

(3) 当加入的未知雷达信号的种类过多时,需对特征提取网络进行扩展训练,而雷达侦察设备中仅存储了样本库中的数据,数据量较小难以支持特征提取网络进行有效扩展训练。

为了解决以上问题,本文在文献[25]的基础上设计了一种基于粒子群优化的具有噪声的密度聚类(density-based spatial clustering of applications with noise based on particle swarm optimization, PSO-DBSCAN)算法和半监督式条件生成对抗网络(semi-supervised conditional generation adversarial network, SCGAN)的未知信号处理算法。主要工作如下:

(1) 利用粒子群优化(particle swarm optimization, PSO)算法提取出具有噪声的密度聚类(density-based spatial clustering of applications with noise, DBSCAN)算法的最优输入参数,之后DBSCAN算法使用此参数对未知雷达信号进行聚类;

(2) 设计了一种距离筛选算法在聚类算法输出的簇中选择出更为可信的样本,并将其扩充到雷达样本库中;

(3) 设计了一种基于SCGAN网络的小样本训练方法,在样本数量较少的情况下实现了网络对未知信号的扩展训练,从而提升模型对未知信号的识别准确率。

1 基础理论

1.1 PSO算法

PSO算法属于群体智能优化算法,是Kennedy和Eberhart基于鸟群社会系统Boid设计的。核心思想是通过粒子来模拟鸟群中的个体,这种粒子不具备质量属性,仅有位置和速度两个属性。每个粒子在粒子群中独立寻求自己的最优解,互不干扰,找到的最优解被称作当前个体极值,并共享到粒子群中。寻找到粒子群中最优的个体极值将其作为当前全局最优解,所有粒子依据和调整自己的位置及速度。反复迭代这个过程,直至满足终止条件。

1.2 具有噪声的密度聚类算法

DBSCAN算法的核心思想是假定样本类别由其分布的紧密程度所决定,同类别的样本紧密相连。依据此假设将紧密相连的样本归到一类,所有样本归到各自紧密程度最高的类别就得到最终的聚类结果。

1.3 条件生成对抗网络

条件生成对抗网络(conditional generative adversarial networks,CGAN)在生成对抗网络(generative adversarial networks,GAN)的基础上增加了额外的条件信息,可以指导性地生成数据。网络结构如图1所示。

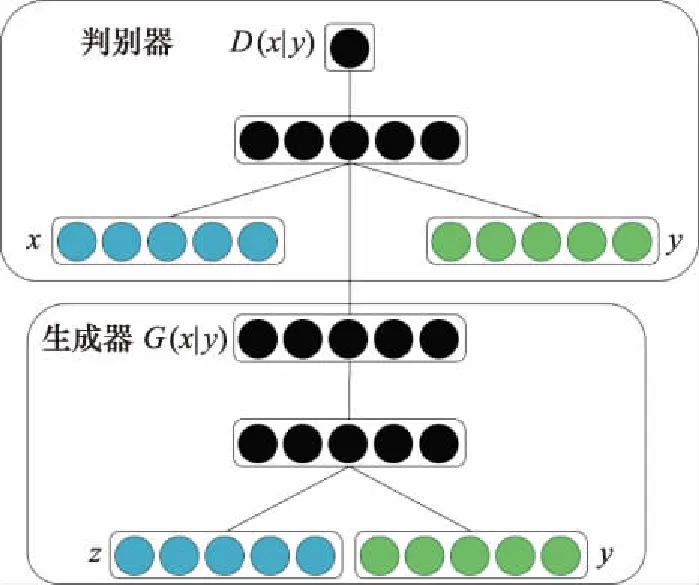
图1 CGAN结构Fig.1 CGAN structure

不同的条件信息有不同的损失函数,可将CGAN看作是不同条件下所有GAN的集合。CGAN可以训练生成器生成指定类别的图像,但其判别器只可判别“真”“假”。

1.4 半监督GAN

与传统GAN网络不同,半监督GAN(semi-supervised learning with GAN,SGAN)的判别器采用Softmax分类器作为输出层,以解决多分类的问题。网络结构如图2所示。假设数据集类别数目为,那么判别器(discriminators,D)的输出层的维数被设置为+1,第+1类表示生成器(generators,G)输出的伪造数据。这样判别网络既可以判定输入数据的真假也可以对真实的样本进行分类,在这种情况下,判别器D也是一个分类器(classifiers,C),故可称其为D/C网络结构。SGAN网络同时训练生成器和半监督式分类器,训练出来的生成模型成像效果更好、半监督式分类器性能更优。判别网络通过学习标签样本的类别分布信息以及无标签样本的数据分布信息来指导生成网络提高生成样本的质量,减少其训练时间。

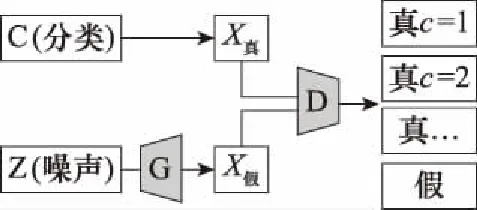
图2 SGAN结构Fig.2 SGAN structure

2 基于PSO优化聚类的未知信号样本提取

2.1 PSO-DBSCAN聚类算法

本文通过PSO优化算法寻求DBSCAN算法中的最优参数后,利用最优参数构建最优DBSCAN聚类模型后对未知雷达信号进行聚类,得到聚类结果。

2.1.1 适应度函数的选择

适应度函数也称为目标函数,是需要被优化的目标。在本问题中,为评估聚类算法聚类效果的优异,可以使用一些聚类度量函数进行评价。在类别数未知的情况下,主要有轮廓系数、CH(Calinski Harabasz)分数和戴维森堡丁指数(Davies Bouldin index,DBI) 3种。在PSO算法中,粒子位置信息的调整过程是在寻求适应度函数最小值的过程,最优解与适应度是负相关关系。3种评价指标中仅有DBI的大小和聚类效果呈负相关。因此,本算法选择DBI指数作为PSO算法中的适应度函数,数学表达式为

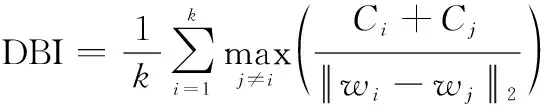
(1)

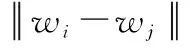
212 算法设计

本算法的维度搜索空间设置为2,适应度函数为聚类效果评价函数DBI,算法的流程如下:

将未知雷达库中的信号输入文献[25]构建的网络,得到各个信号的特征向量。

将DBSCAN算法的两个输入参数(eps和MinPts)作为优化对象,初始化PSO算法。

根据式(1)计算每个粒子的适应度值,以各粒子对应的参数构建聚类模型,对未知信号的特征向量进行聚类,根据各个模型的聚类结果计算DBI指数,将计算结果作为各粒子的适应度值。

根据PSO算法分别对粒子的位置和速度进行更新。

根据PSO算法分别对个体极值和全局极值进行更新。

判断是否达到迭代次数。若达到次数,返回最优极值的取值;否则,返回步骤3。

利用最优参数构建最优聚类模型。

使用最优聚类模型对未知信号的特征向量进行聚类得到聚类后的标签。

2.2 基于距离筛选的样本选择算法

受到无监督学习本身性能的限制,PSO-DBSCAN算法的聚簇准确率较高,但是总体准确率欠佳,即一个簇中包含着许多本属于其他簇的数据。为保证扩充到样本库中数据的准确度及可信性,提出了一种基于距离筛选的样本选择算法,算法的流程为

设置数量阈值和需要选取的样本数量。

判断一个类别中的个体总数是否小于,若小于将该类别记作噪声点舍去,否则计算该类别各个元素间的距离,得到距离矩阵,其数学表达式为

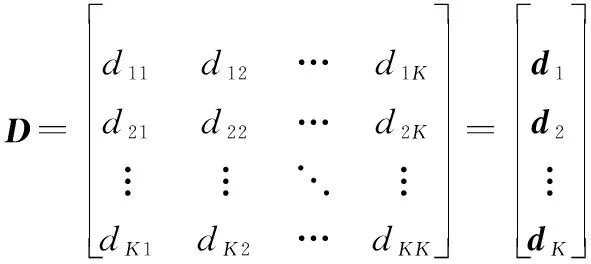
(2)

求出中除了主对角线上的元素外最小的2个值,将其行和列的索引存入索引数组。

求出中出现次数最多的两个元素,存入样本数组,分别记作、。

找到中的最小元素,索引记作并将()的值设置为中的最大值。

判断是否属于,属于则返回执行步骤5,否则执行步骤7。

判断()是否大于的中位数,若大于返回执行步骤5,否则执行步骤8。

将存入样本数组,判断中元素的数量是否小于,若是执行步骤9,否则输出直接退出算法。

判断中所有元素是否相同,相同则执行步骤10,否则返回步骤5。

将中的样本随机进行复制,使其数量为,结束算法并输出。

核心思想是从一个簇所含有的所有个体中,选取出个相互之间的距离都比较小的个体作为样本,以对样本库进行扩充。

3 基于SCGAN网络的小样本训练

3.1 模型概述

通过PSO优化聚类和基于距离的样本选择算法后,可以得到可信度较高的正确样本,以此对样本库进行扩充。但从文献[25]相关实验可知,当加入的未知信号的种类过多时,在不经扩展训练的情况下单纯扩充样本库会降低识别算法的准确率,需要使用未知信号和已知信号一起进行扩展训练。由于筛选出的未知样本以及样本库中已知样本的数量较少,难以构成足够多的一般三元组,不足以支持ResNet网络进行有效训练。因此,结合文献[25]中的ResNet网络,借鉴CGAN、SGAN,设计了一种基于SCGAN的小样本训练方法,解决了三元组数量不足的问题。

本模型的生成器G借鉴了CGAN的思想,将标签信息和噪声合成在一起作为输入,以产生多类别的输出,但是如果要求其像CGAN一样生成和真实数据极其相似的伪造数据,对于网络结构和训练时间上的要求比较严格。因此本模型在判别器方面则借鉴了SGAN的思想,其输入是样本库中的真实数据和伪造数据的集合,通过尽可能地调节生成器,使得其输出的伪造数据和真实样本之间可以构成一般三元组的条件,以解决少样本训练的问题。SCGAN的系统框图如图3所示。

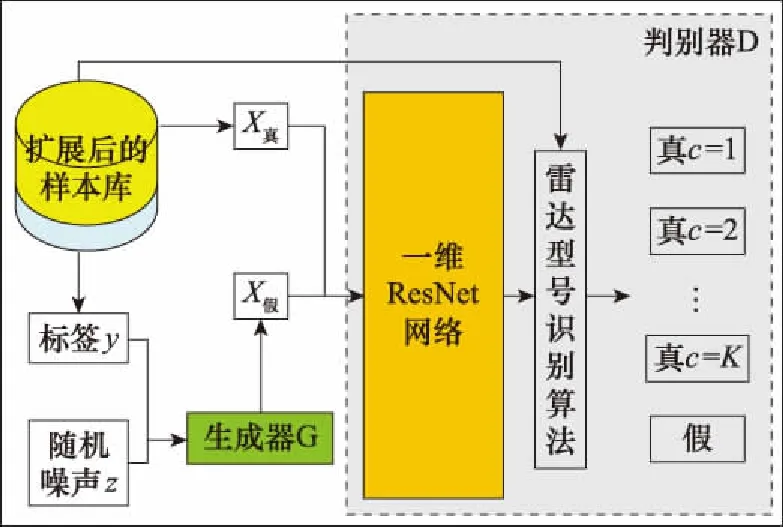
图3 SCGAN结构Fig.3 SCGAN structure

由图3可以看出,生成器借鉴了CGAN的思想,其输入为一个随机噪声和真实数据库中的标签的叠加,目的是使模型可以生成多种类别的“伪造数据”,同时要求生成的数据与真实数据相似,并将其标签设置为-1(与所有类别的标签均不同);另一方面,判别器的设计与SGAN相似,但由于本模型的目的是解决ResNet网络在小样本下的训练问题,因此本模型的判别网络直接选用文献[25]的ResNet网络,同时通过文献[25]中识别算法实现对未知雷达信号以及生成器G输出的“伪造数据”的分类。

3.2 模型结构与参数

生成网络使用了一维卷积和维度恢复模块搭配的方式对网络进行构建,其系统框图如图4所示。判别网络与文献[25]的ResNet网络一致,网络结构及输出维度如图5所示。

图4 生成网络结构Fig.4 Generative network structure

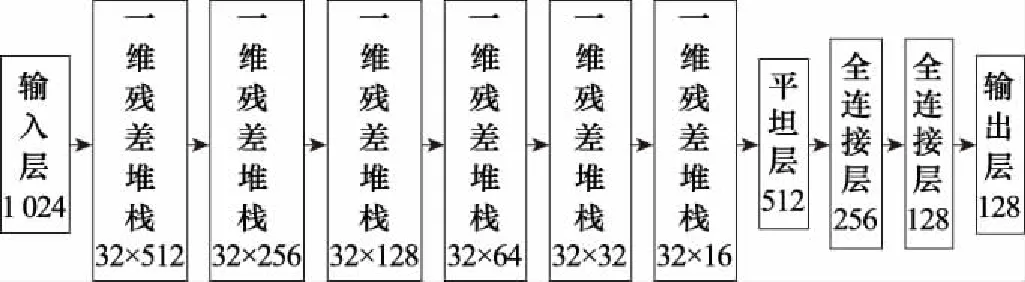
图5 判别网络结构Fig.5 Discriminator network structure

生成网络并未使用上采样层进行维度恢复,因为上采样层适合处理图像数据,但对一维雷达信号会造成不可恢复的损伤。因此本文设计了一种基于全连接层的维度恢复模块,如图6所示。

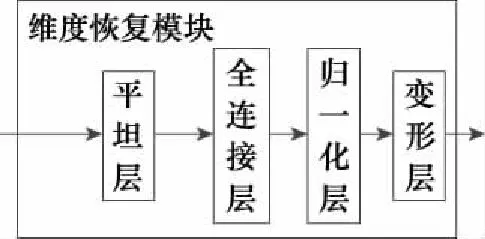
图6 维度恢复模块Fig.6 Dimension recovery module

3.3 损失函数设计

首先考虑生成网络,生成网络的作用是根据输入数据的类别产生与其相近的信号,从而使其输出的“伪造数据”可以和样本库中的真实数据组成足够多的一般三元组。一个三元组由锚元素(anchor,A)、正元素(positive,P)和负元素(negative,N) 3个元素组成。其中A、P属于同一类别下不同样本,N是与A、P不同类的样本。对于一个三元组来说,将A、P、N 3个元素输入某个神经网络,可得到其各自在特征空间的映射,分别记作()、()和()。生成网络损失函数设计如下：

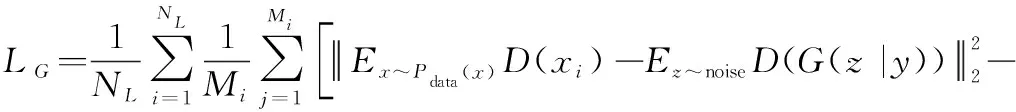
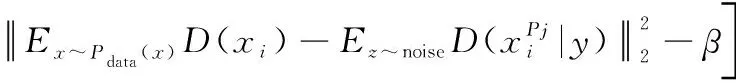
(3)

由式(3)可知,生成网络损失函数是使(())到()与()到()间的距离趋近于阈值。因此,只要合理地设置,使其位于0～(三元组距离阈值)之间,就可以使生成器的输出与样本库中真实数据之间满足一般三元组的条件,从而形成足够多的一般三元组以达到判别网络的训练要求。

判别网络的损失函数设计如下：

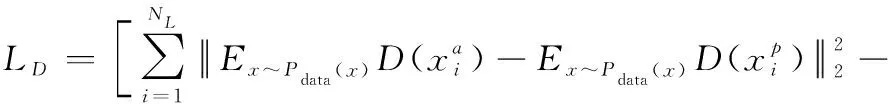
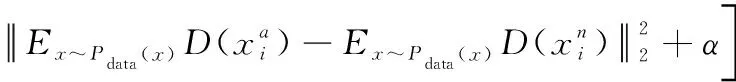
(4)

由式(4)可知,判别网络的损失函数本质上依旧是三元组损失函数,只是对三元组的选择方式进行了调整。在中,三元组元素和元素的选择仅来自于样本库中的真实数据,而元素的选择来自于真实数据和“伪造数据”的混合,而且“伪造数据”中包含了大量的一般三元组,因此解决了样本过少时三元组数量不足造成网络难以训练的问题。

4 仿真实验与算法验证

4.1 验证PSO-DBSCAN算法

本文通过Matlab生成数据对PSO-DBSCAN算法的可行性和有效性进行测试。其中,未知信号标签设置为-1,信噪比在-20～10 dB之间,共生成8部雷达信号,每种信号每隔2 dB生成100个样本,样本长度设为1 024,样本总计12 800个。其余参数设置如表1所示。

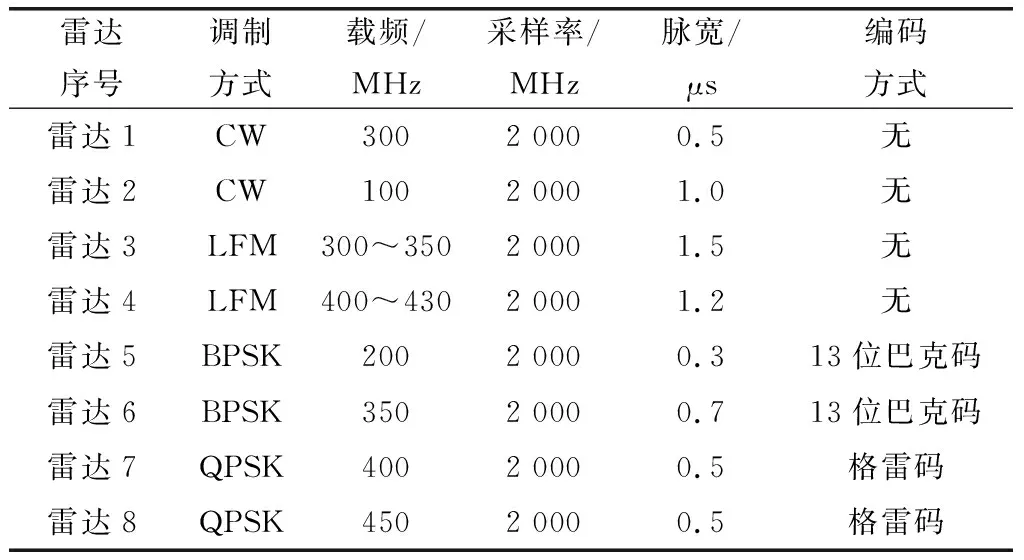
表1 数据集组成Table 1 Data set composition

PSO算法粒子数量为30,粒子维数为2,最大迭代次数为100,惯性因子为08,学习因子1、2均为2,随机数1、2在[0,1]区间内均匀配置。主要测试两项指标:一是聚类数量的准确率,测试算法聚出的类别数目是否准确,称之为聚簇准确率;二是总体聚类效果的准确率,是测试算法把属于同一类别的个体聚类在一起的能力,称之为总体准确率。对每种类别情况进行100次蒙特卡罗实验,取平均值作为测试结果,结果如图7所示。实验发现,两种准确率在输入数据的类别数量处于2～5时比较准确,且聚簇准确率要远高于总体准确率,原因是聚类算法属于无监督训练,其总体准确率自然不会太理想,而聚簇准确率只是反映算法能否分出正确的簇数,其难度相对较小,聚簇准确率也相对较高。

图7 算法的识别准确率Fig.7 Algorithm recognition accuracy

而在输入的类别只有1类时,两种准确率都不高,聚簇准确率直接变为了0。该现象出现的原因是当类别只有1类时PSO算法的适应度函数(DBI分数)不能计算(会输出一个较大值),从而使得PSO-DBSCAN算法不能聚出1类。针对此问题,本文给出的解决方法是向未知信号集合中加入一种人为设置的“区别数据”(设置为零向量),以保证未知雷达库中至少包含两类信号。区别数据由于每个个体的特点较突出(是零向量),因此很容易和其他类别区分开来,在聚类结束后,将区别数据剔除即可。

算法改进的示意图如图8所示。改进后的准确率情况如图9所示。

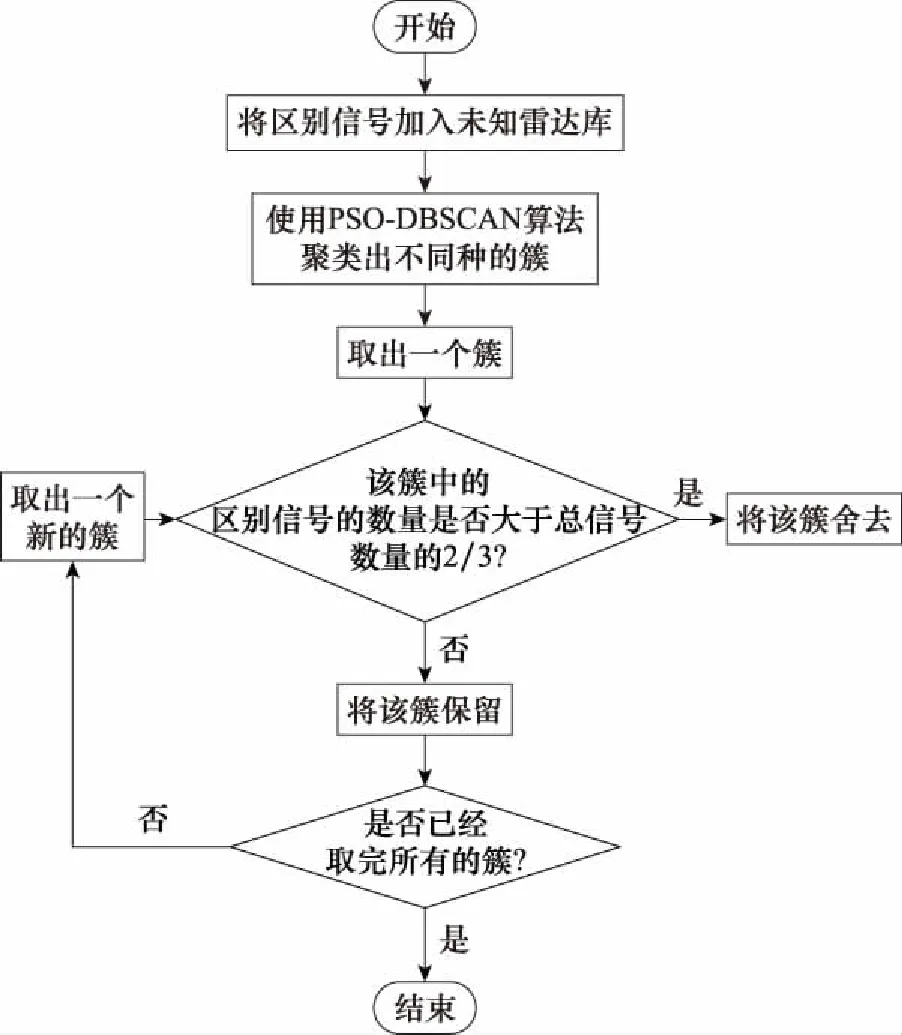
图8 改进算法示意图Fig.8 Schematic diagram of the improved algorithm

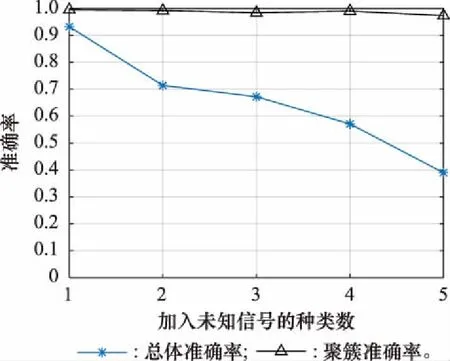
图9 改进算法的识别准确率Fig.9 Recognition accuracy of the improved algorithm

由图9可知,当未知雷达库中只包含一种信号时,改进方法的聚簇准确率有了明显的提升,同时在类别大于1时,算法的性能没有受到影响。因此,本算法的聚簇准确率相对理想,但总体准确率的精度依然不佳,因此需要用样本选择算法从各个簇中选择出更为可信的样本。

4.2 验证样本选择算法

实验1:在第41节的基础上对样本选择算法的有效性进行相关验证。实验条件与第41节中基本一致,样本选择算法的数量阈值和需要选取的样本数量分别设置为100和32,在进行了100次蒙特卡罗实验后,得到的不同种类下本选择算法与随机选择的准确率对比情况如图10所示。

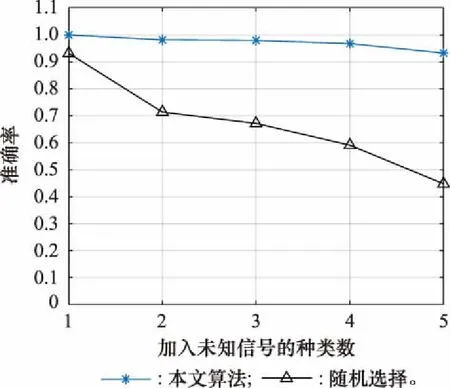
图10 本文算法与随机选择的准确率对比Fig.10 Comparison of accuracy between the proposed algorithm and random selection

由图10可知,基于距离筛选的样本选择算法可以有效筛选出相对纯净的样本,准确率能达到93%以上。即便只使用一种未知雷达信号测试时,由于加入了“区别数据”,使得PSO-DBSCAN得到的聚类结果或多或少会包含一些“区别数据”,此时随机选择方法也会选到“区别数据”,而本方法的正确率则可以达到100%。当未知信号的种类数较多时,本算法的性能要远高于随机选择方法。

实验2:参数和对算法的性能有一定程度影响,由于是为了排除数量达不到要求的簇,一般是确定值,因此对不加考虑。而的选择则对算法的影响较大。本实验主要目的是验证簇的规模(用每个簇所包含的个体数量衡量)与的取值对样本选择算法准确率的影响。实验结果如表2所示,最优识别率加粗显示。

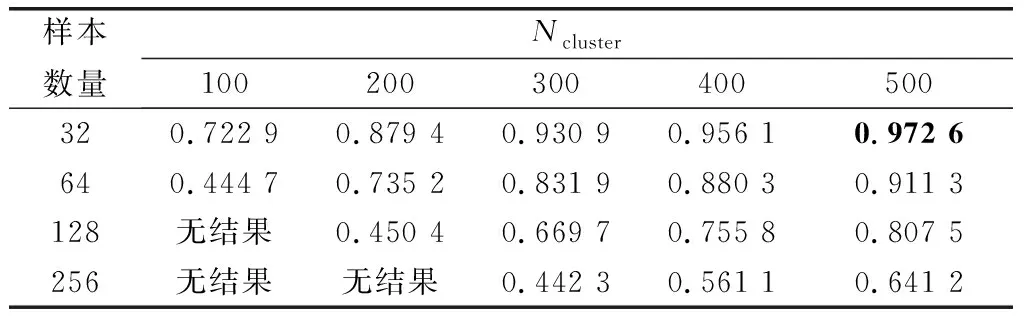
表2 簇规模Ncluster与参数N对算法准确率的影响Table 2 Impact of cluster size Ncluster and the parameter N on algorithm accuracy

由表2可知,簇的规模越大、样本选择数量越小时算法的准确率越高,即算法可以有效地从大规模的簇中选择出少量的正确样本。当簇的规模一定时,增大会使得算法的准确率下降,符合实验猜想。

4.3 验证SCGAN小样本训练样本

实验3:本实验使用扩展后的样本库对SCGAN进行训练以验证本算法的可行性,训练过程中损失函数值变化情况如图11所示。

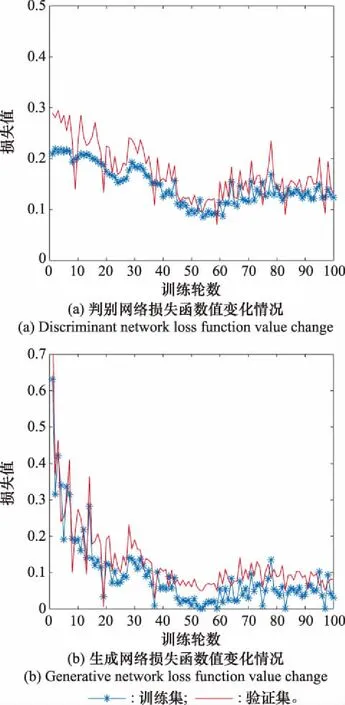
图11 SCGAN训练情况Fig.11 SCGAN training situation

由图12可知,模型的拟合情况良好,并未出现过拟合情况。

实验4:为了体现本方法在小样本训练方面的优势,使用不同数量的样本库对SCGAN网络和ResNet网络进行训练,信号识别准确率对比情况如表3所示。

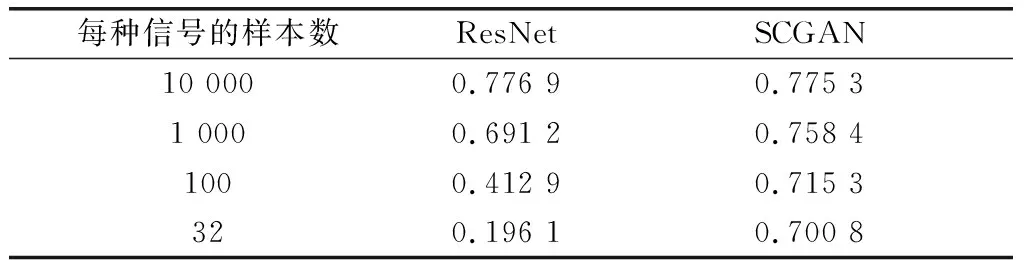
表3 信号识别准确率对比Table 3 Signal recognition accuracy rate comparison

由表3可知,当样本库中的样本数量足够多时,二者性能相近,ResNet网络的识别准确率甚至略高于本模型,但随着样本数量的减少,SCGAN的优势逐渐体现出来。当每种信号的样本数为32时,ResNet网络已经不能实现有效训练,但本算法仍可以保持70%的准确率。由此可知,SCGAN网络可以解决小样本下训练问题。

5 结 论

在实际工作中雷达信号侦察设备会接收到大量的未知信号,本文基于课题组在已知雷达信号识别的基础上围绕未知信号识别问题进行了一系列研究:首先使用PSO-DBSCAN算法对未知雷达库中的信号进行初步聚类;之后采用基于距离筛选的样本选择算法在聚类算法输出的簇中选择出更为可信的样本对雷达样本库进行扩充;最后针对样本库中数据不足以构成一般三元组进行训练的情况构建SCGAN网络实现了小样本下ResNet的扩展训练。仿真实验证明,本方法可以实现未知雷达信号的分类识别。