波浪作用下基于不同负载的一种Savonius型水轮机捕能性能研究

黄炎晨，黄方平，刘 静

(1.江西理工大学，江西 赣州 341000；2.浙大宁波理工学院，浙江 宁波 315100)

在当今社会经济发展的高速阶段，能源的重要性日益凸显，以化石能源为主导的发展模式面临着严峻挑战[1]。在这样的背景下，可再生能源作为一种储量巨大的环境友好型能源，让人们看到了替代化石能源的可能。可再生能源主要包括太阳能、风能、地热能、氢能、海洋能等几大类[2]。这几种能源中海洋能具有极大的优势，其形式多种多样，大致包含潮汐能、潮流能、波浪能、盐差能等，不同形式的海洋能对应着不同的开发利用技术。常见的波浪能利用技术有：振荡水柱(OWC)技术，波浪振荡压缩空气实现能量转化利用；越浪式技术，将波浪能转化为机械能；点吸收技术，利用波浪升沉运动吸收利用能量[3]。

在海洋能利用上，水轮机常用于捕获潮流能，相比于其他海洋能捕能装置，水轮机转动噪音小，便于和发电装置连接，其旋转方向不受来流运动方向影响，无需换向机构，极大简化了整体结构[4]。水轮机将捕获的能量经由传动装置带动电机转动发电，完成能量的转换与利用。这过程涉及了水轮机捕能性能的研究[5]。Savonius型水轮机是一种典型的水轮机，桨叶是其关键部位。Savonius型水轮机桨叶(以下简称Savonius型桨叶)叶片结构简单，制造成本低，启动时转矩相对较大且转速相对较低，但其缺点是功率系数相对较低。而Savonius型水轮机用于捕获波浪能的对应研究相对较少，也缺少相关的成熟应用。参照Savonius型水轮机捕获潮流能时的安装方式，在捕获波浪能时，按波浪运动方向与水轮机旋转轴的方位不同，将水轮机的安装分为水平式安装和垂直式安装。Savonius型水轮机利用波浪水质点圆形轨迹运动作用在桨叶凹凸叶面上的阻力差旋转做功。有着与捕获潮流能时相近的优点，但也面临同样的问题，桨叶的能量转换效率相对较低，捕能性能的局限性限制了其应用，因此如何提高Savonius型桨叶的能量转换效率，使其捕能效果达到最优，一直是多年来研究的重点[6-7]。在研究过程中，研究人员往往忽略桨叶在不同波浪情况下其所承载的负载变化对其性能的影响[8]。因此，文中研究波浪作用下一种Savonius型桨叶在不同负载下运转的转速和扭矩以及功率等变化，总结桨叶性能变化趋势，评价捕能效果，为在实际海域中水轮机的结构设计和工程应用提供参考。

1 试验研究

1.1 试验条件

整体的物理试验研究将在一座尺寸为70 m×4 m×4 m(长×宽×高)的水池移动平台上进行。试验布置如图1所示。摇板式造波机由伺服电机推动摇板可产生波形稳定、可重复的规则波。桨叶安装于平台上，通过传动装置进行传动，磁粉制动器作为负载并连接传感器，动态扭矩传感器采集Savonius型桨叶的试验运动数据，并将桨叶的速度、扭矩等数据传输给电脑。

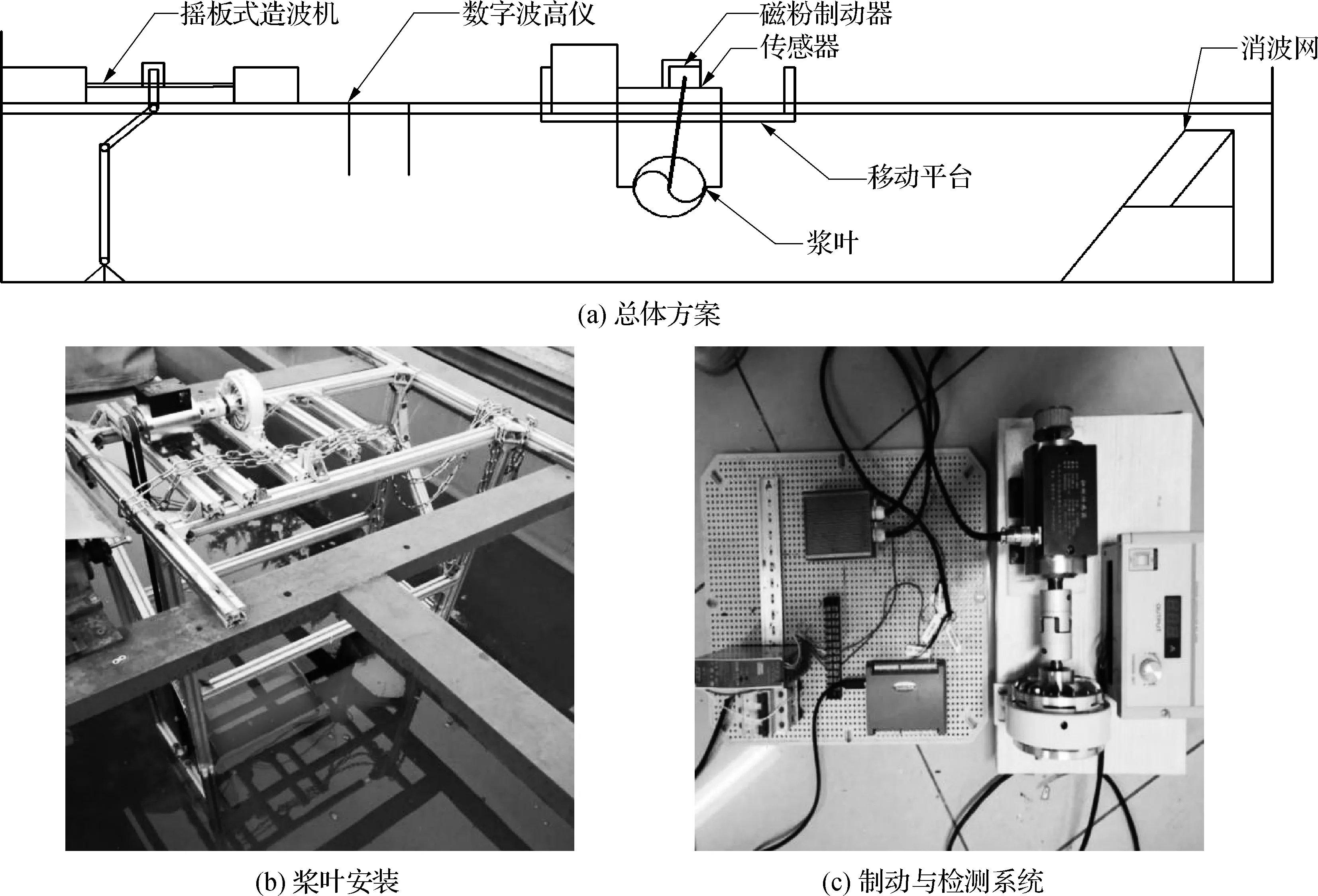
图1 试验布置

一级桨叶由于其特定的叶片几何形状，水流会在桨叶两侧都产生扭矩，使得桨叶运转时扭矩波动大，在某些特定角度会需要较大的启动转矩，甚至产生负转矩。为避免对试验造成不利影响，选择将两个一级Savonius型桨叶彼此叶轮成90°偏角组合成二级Savonius型桨叶。

试验证明二级桨叶有更好的启动性能，两叶轮互成90°偏角也使得桨叶重心分布均匀，运转更平稳[9]。桨叶外框架由刷漆的3 mm铁板焊接而成，保持整体结构稳定，S形叶面为高密度聚乙烯(HDPE)材料具有抗腐蚀性，使桨叶能在海水环境下正常工作，叶面一半涂为红色，使得运转更为清晰直观。根据波浪运动，采用水平布置方式可使桨叶最大限度捕获能量。桨叶高H=0.92 m，直径D=0.50 m，高径比H/D=1.84，重叠率(e-0.02)/D=0.16，中间贯穿轴直径0.02 m。具体如图2所示。

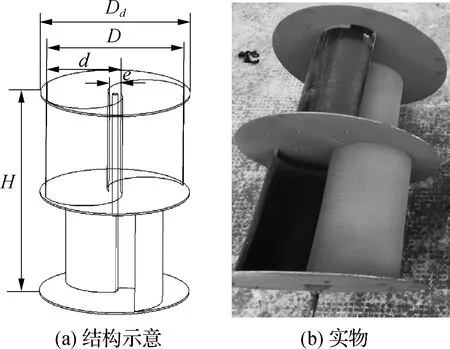
图2 Savonius型桨叶

1.2 试验设置

水池中推板冲击水面造出不同周期不同波高的规则波，波高仪放置于移动平台前2～3个波长处以确定波浪具体参数。桨叶长0.92 m，直径0.50 m，旋转轴的入水深度为0.35 m(叶轮直径的7/10)。通过改变磁粉制动器的输入电流改变负载值，通过同步带传动，由传感器测量转速和扭矩，分析在不同波浪和不同负载作用下桨叶的性能。考虑到初始波浪的撞击与破碎，采集时间40 s以上，规则波试验的波浪数据采集时间间隔小于平均波周期的1/20，采集频率为50 Hz。依据我国《海港水文规范》(JTJ 213-98)[10]，参考当地近海水文数据，根据相似原则并结合波高仪所测得的水池波浪数据，依据现有条件，试验波浪取3种不同周期，分别为1.3 s、1.6 s、2.0 s，每种周期再取对应的不同4种间隔相对均匀的波高，使波浪满足试验要求且尽可能接近实际情况；所加负载间隔0.3 N·m，从0逐渐递增至2.1 N·m共8组，其中0负载组作为转速参照，不进行扭矩对比。根据波浪的不同周期、波高以及所加的不同负载，共进行96组试验，具体参数变量如表1所示。

1.3 试验结果分析

在波浪周期1.3 s，1.6 s和2.0 s情况下，测得不同负载时桨叶的平均转速和平均扭矩，如表2、表3、表4所示。由各表可知在小负载条件下桨叶的转速基本不变，维持在一个较高水平，其平均扭矩相对较小；当负载过大时，桨叶转速维持在一个极低水平，基本认为转速低于7 r/min则桨叶无法捕获有效能量，此时可近似认为桨叶停止转动；当负载达到某一值，转速出现明显跳跃，此时平均扭矩近似等于所加负载。当波高低于100 mm将无法推动桨叶转动。

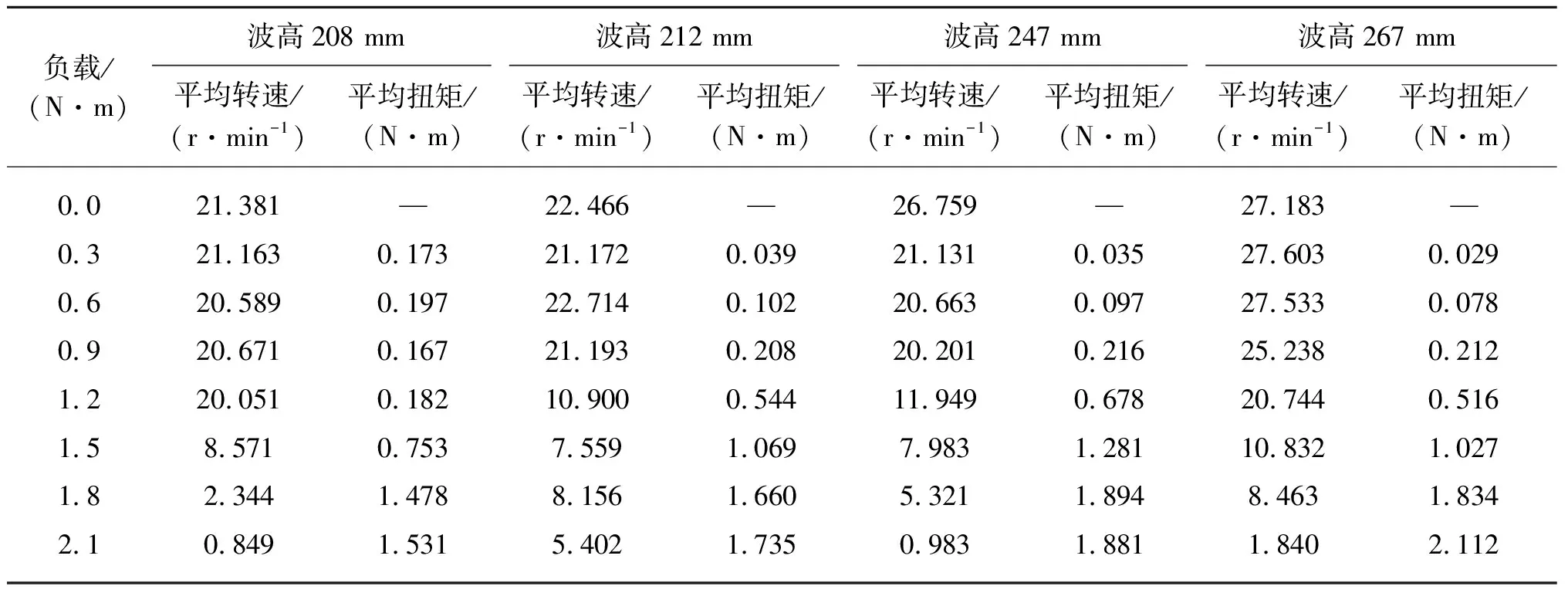
表2 波浪周期1.3 s测得桨叶平均转速和平均扭矩

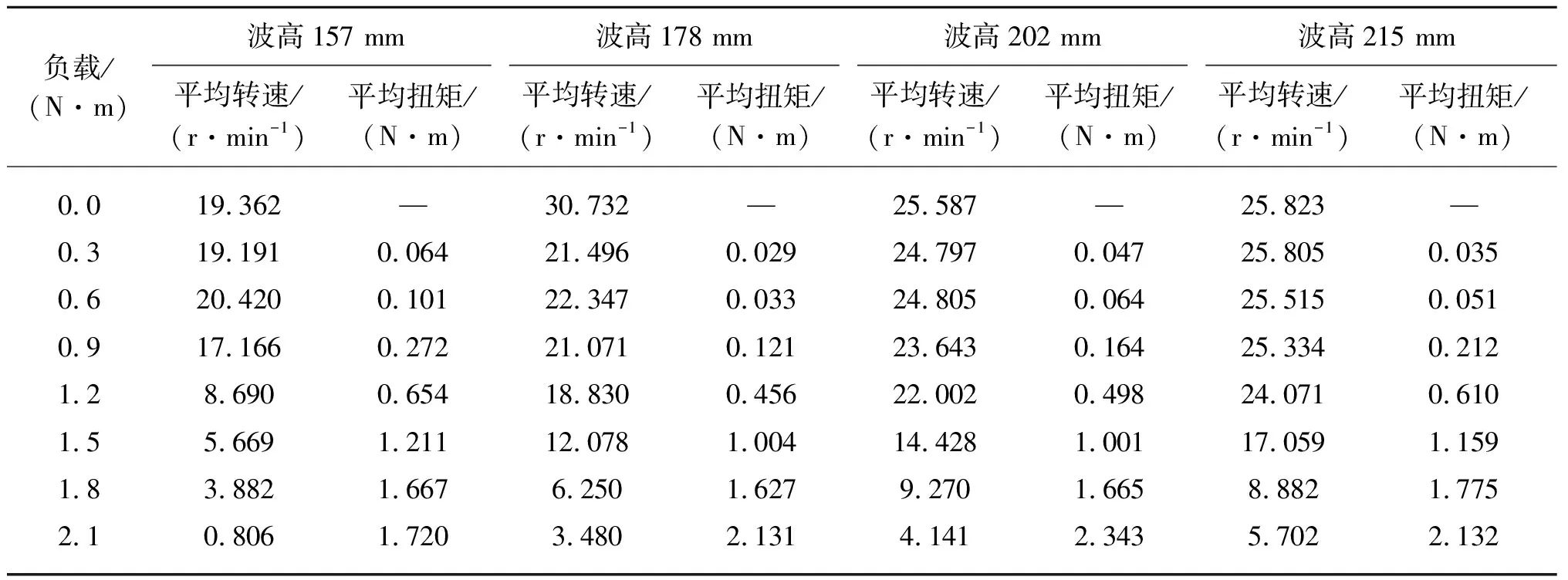
表3 波浪周期1.6 s测得桨叶平均转速和平均扭矩

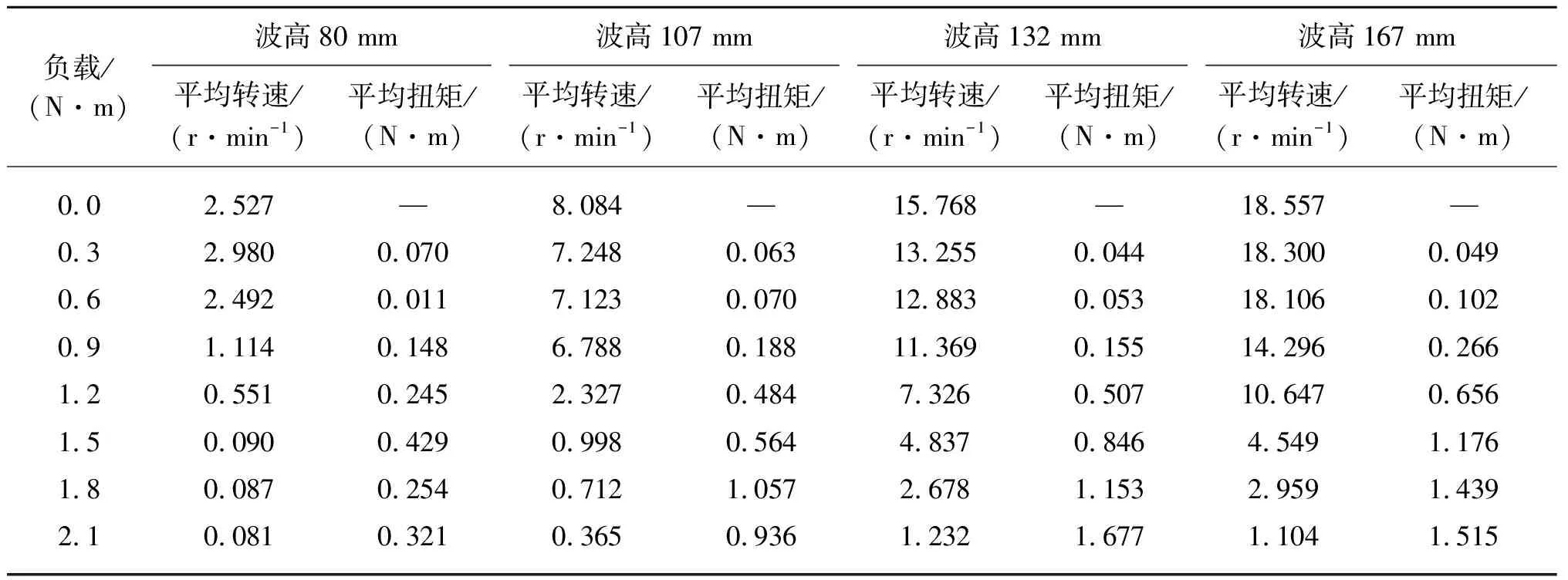
表4 波浪周期2.0 s测得桨叶平均转速和平均扭矩

桨叶捕获的功率为所测平均转速和平均扭矩的乘积，不同波浪作用下桨叶功率随所加负载变化如图3所示。可知功率曲线随着负载增加先上升再下降，在中间某个位置达到峰值。不同波浪作用下，峰值出现点不同。波浪周期1.3 s时峰值位于负载1.8 N·m处，波浪周期1.6 s时峰值位于1.5 N·m处，波浪周期2.0 s时峰值位于负载1.2 N·m处。

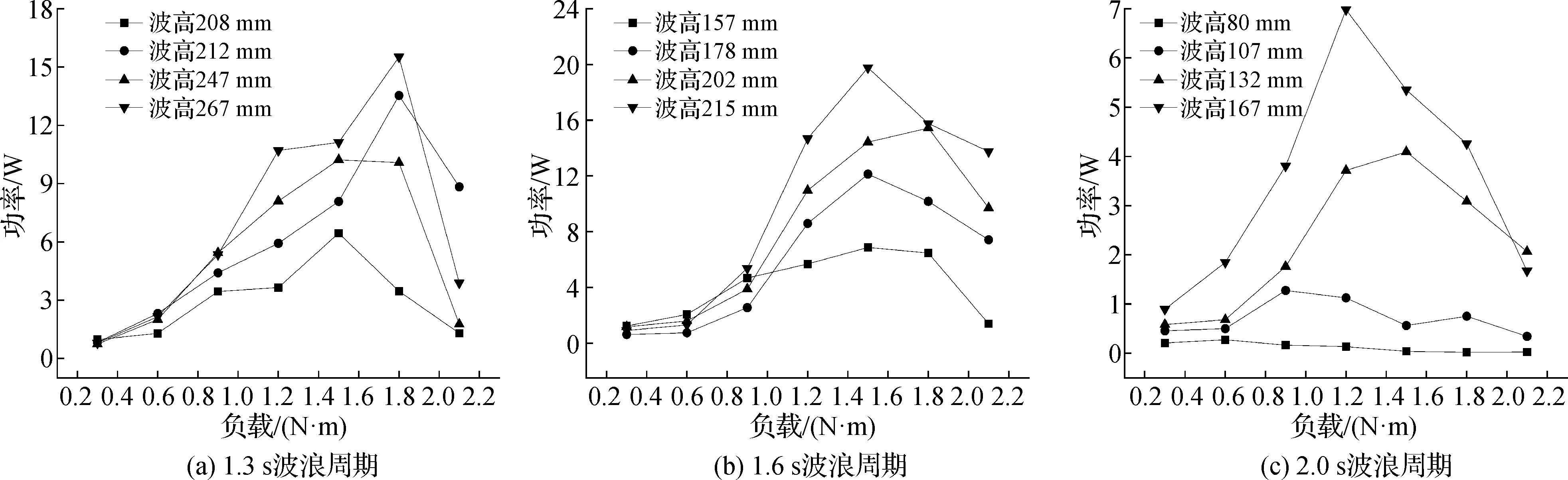
图3 桨叶功率随负载变化

2 数值仿真

2.1 试验设置与模型建立

为保证仿真与水池试验的一致性，根据其试验组数安排，仿真设置1.3 s，1.6 s和2.0 s的3种周期波浪和各自对应4种不同的波高，再对桨叶施加负载，负载从0.0～2.1 N·m变化，每次间隔0.3 N·m，共有8组。具体参数变量如表1所示。

建立与实际桨叶尺寸1∶1的数学模型，桨叶的模型高0.92 m，直径0.50 m，为减少不必要计算，取消桨叶模型的轴。模型如图4所示。

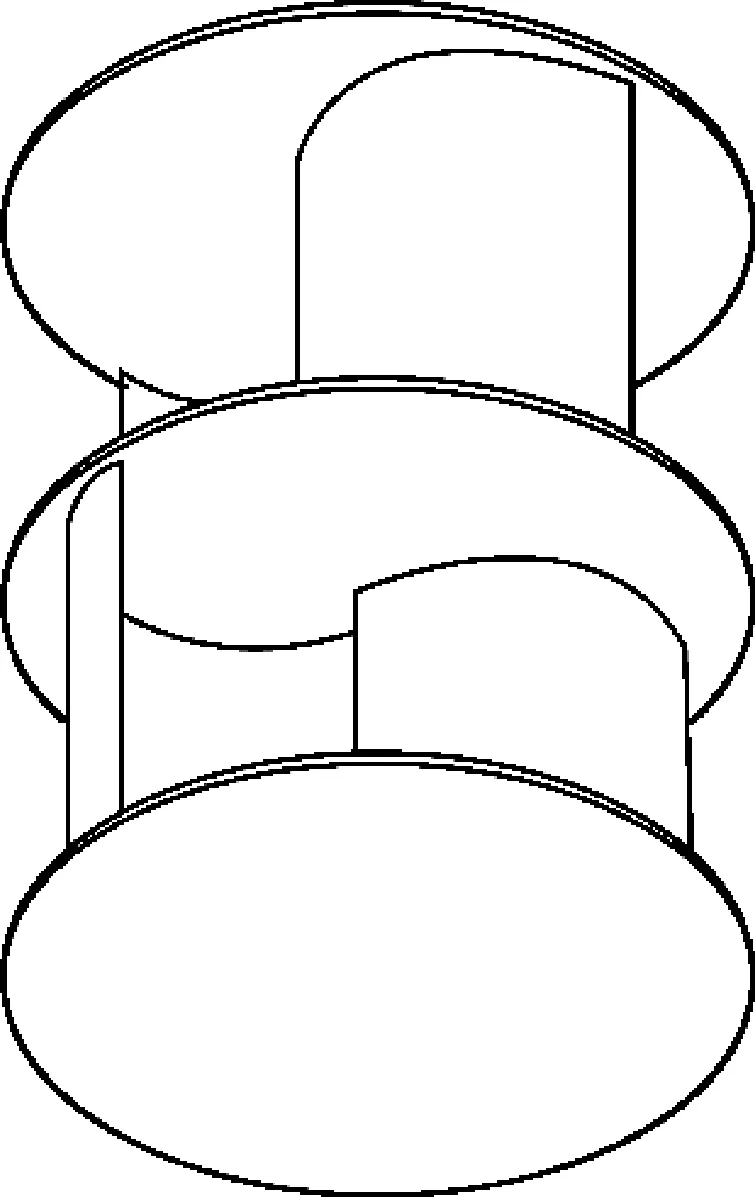
图4 桨叶模型

2.2 控制方程

数值模拟采用StarCCM+软件，假设流体不可压缩，计算时忽略流体表面张力，黏性系数不变条件下，控制方程如式(1)～(5)所示。

Navier-stokes方程，沿x、y、z共3个方向的动量守恒[11-12]为：

(1)

(2)

(3)

连续方程为：

(4)

自由液面方程为：

(5)

式中：ρ为流体的密度；t为时间；u、v、w为沿x、y、z方向的速度分量；p为流体压强；μ为黏度；Su,Sv,Sw为x,y,z方向上的分量；s为边界条件；ct为构建函数；U为流体速度，Ud为S在n方向上的分量。

2.3 湍流模型

在试验中，当波浪接触到桨叶叶面，推动桨叶运动时，桨叶周围波浪会发生相对剧烈的运动[13-14]。RNG k-ε模型运用了重整化的数学方法，在计算中考虑了流体流动中，旋转流动状况和小尺度上的平均影响。因此在模拟中选择RNG k-ε模型，其耗散率中的ε为：

(6)

式中：ρ为流体的密度；ui为湍流黏度，其表达式为ui=ρCμk2/ε，Cμ为经验系数，k和ε为输运方程的两个基本参数；xk为沿x方向的湍动能[15]。

2.4 边界及初始条件设置

边界条件设置是数值模拟计算中相当重要的一步，规划一个区域作为计算所需的水域，根据物理试验的条件，设定水域尺寸为70 m×4 m×4 m(长×宽×深)，设置确定包括速度入口、压力出口、壁面等条件。一般认为运动学的边界条件为：

(7)

另一种动力学边界条件为：

(8)

2.5 网格设定

网格参数的设定主要分为：网格基本尺寸和网格类型。在仿真模拟中，对于连续体网格模型选择切割体网格生成器及棱柱层网格生成器。为确保计算结果的精确性，既不能把网格划分太稀疏导致结果失真，也不能让网格划分太过稠密增加不必要的计算量，因此在自由液面形成的波浪，在其振幅所能达到的范围内进行加密网格操作，波陡为波高与波长的比值，当波陡超过0.04时，波高方向和波长方向网格比例尺选1∶4，反之为1∶2，选择网格加密并使网格平滑过渡，网格随着与自由液面距离的增大而逐渐增大。同时由于桨叶转动，采用减运算的布尔操作，调用重叠网格的方式对减运算的网格和背景网格进行合理布局。模型位于基准面两侧，如图5所示为位于基准面一侧的模型网格划分，自由液面网格加密如图6所示。

图5 模型网格

图6 自由液面网格加密

2.6 求解器设置

为提高计算精度，采用二阶时间离散。时间步长的设定，对计算结果的准确性以及计算的收敛性等都有较大影响，其数值的确定与网格大小有关，根据经验公式Δt=T/(2.4n)确定时间步长，其中T表示造波的周期，n表示单位波长划分的网格数。设定最大迭代次数、最大物理时间等参数来形成时间截止条件。依据结果的准确性进行最大迭代次数的调整，根据计算结果及残差是否稳定等因素确定计算的最大物理时间。

2.7 模型仿真

在笛卡尔坐标系下进行桨叶的水动力模型配置，在StarCCM+软件中进行仿真计算，如图7所示。模型选择三维、隐式非定常、欧拉多相流、湍流、状态多项方程、流体体积(VOF)波等。模拟介质包括水和空气两相，通过VOF模型捕捉自由液面。

图7 桨叶仿真

2.8 仿真结果分析

对比试验数据和模拟结果，两者桨叶的平均转速和平均扭矩数值较为接近，且在1.6 s波浪周期条件下，桨叶的运动性能最好。对于桨叶随负载变化的功率曲线，3种波浪周期条件下各取其中一个波高进行对比，如图8所示，分别表示为周期1.3 s波高212 mm、周期1.6 s波高215 mm和周期2.0 s波高132 mm的波浪条件下桨叶功率随负载变化曲线的对比。可知试验和模拟所得数值大体接近，功率曲线变化趋势基本相同，曲线随负载的增大呈先上升后下降趋势，功率最大值所对应的负载区间也相对吻合。结合图3、图9可知，在1.3 s和1.6 s短周期波浪条件下，桨叶有相对良好捕能效果，于1.5～1.8 N·m的负载区间内出现功率峰值；在2.0 s长周期波浪条件下，于1.0～1.2 N·m的负载区间出现功率峰值，对比短周期波浪，其达到功率峰值的负载区间相对提前，功率过早开始降低，且整体的功率曲线随负载变化幅度较低，不具备良好运动性能，整体捕获功率基本都在5 W以下，属于无法有效捕获的能量。由对比可知，该Savonius型桨叶在相对较短的波浪周期条件下能达到较好的捕能性能。

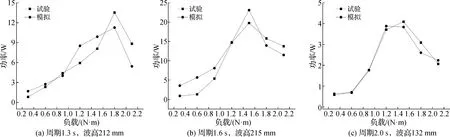
图8 桨叶功率对比

对仿真运算结果进行整理，桨叶转动的平均转速和平均扭矩如表5、表6、表7所示。从中可得在1.3 s和1.6 s的两种波浪周期条件下，桨叶都有相对稳定的运动，而在2.0 s的长周期波浪条件下，桨叶运动性能较差。随着负载的增加，转速逐渐减小，过程中数值有明显的跳跃，扭矩逐渐增大且越来越接近所加负载值。在小负载阶段，即0.3～1.2 N·m的负载区间，扭矩之间的变化幅度较小，此时桨叶的转速处于相对较快阶段。当扭矩接近负载，所处位置正是桨叶速度开始跳跃，数值大幅度变化的对应区间。1.3 s波浪周期条件下，负载达到1.5 N·m时转速跳跃，1.6 s波浪周期条件下，负载位于1.2～1.5 N·m区间时出现转速跳跃，2.0 s 波浪周期条件下，负载位于0.9～1.2 N·m区间出现转速跳跃。

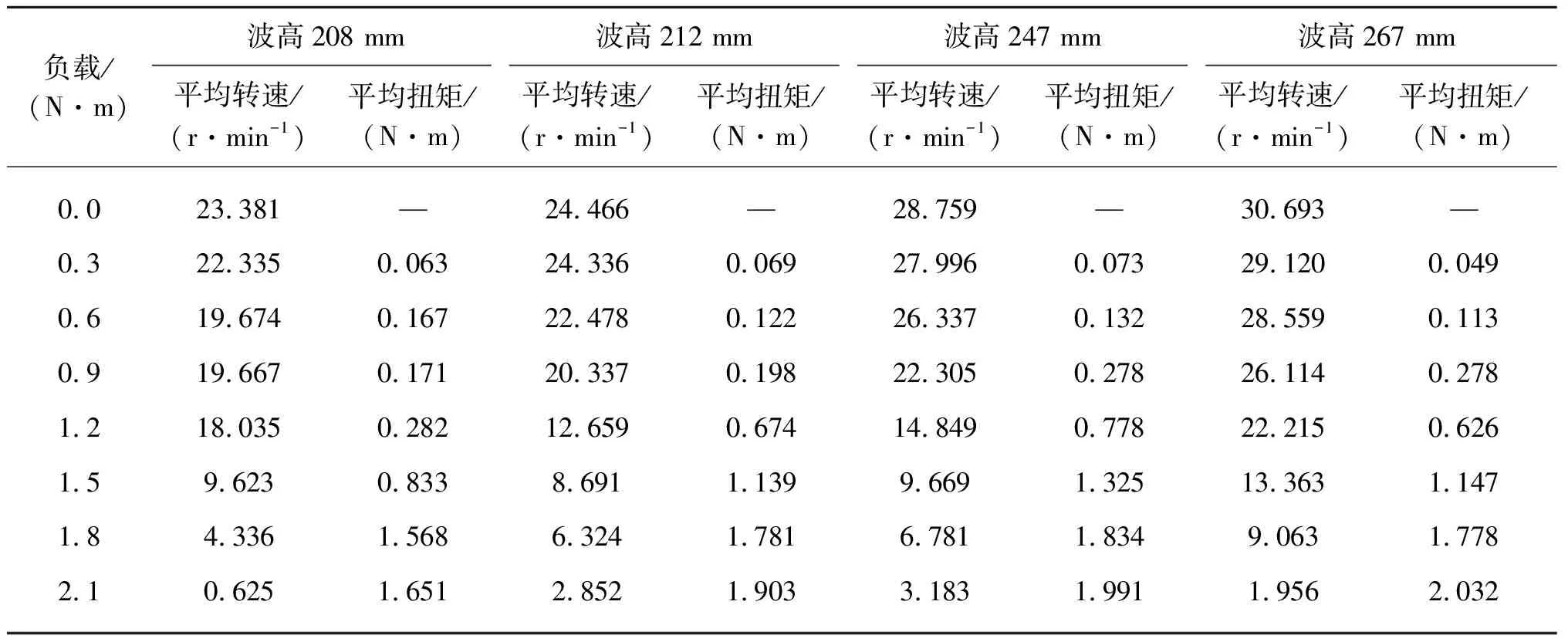
表5 波浪周期1.3 s测得桨叶平均转速和平均扭矩

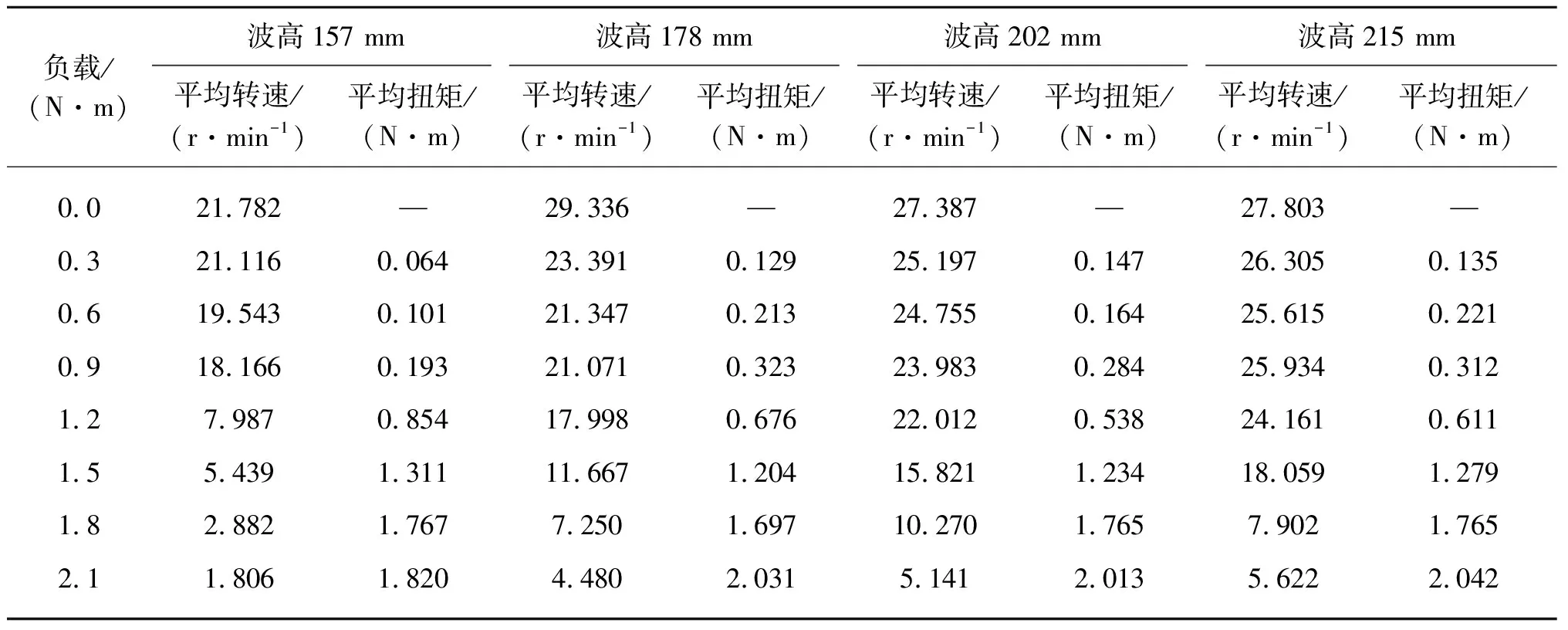
表6 波浪周期1.6 s测得桨叶平均转速和平均扭矩

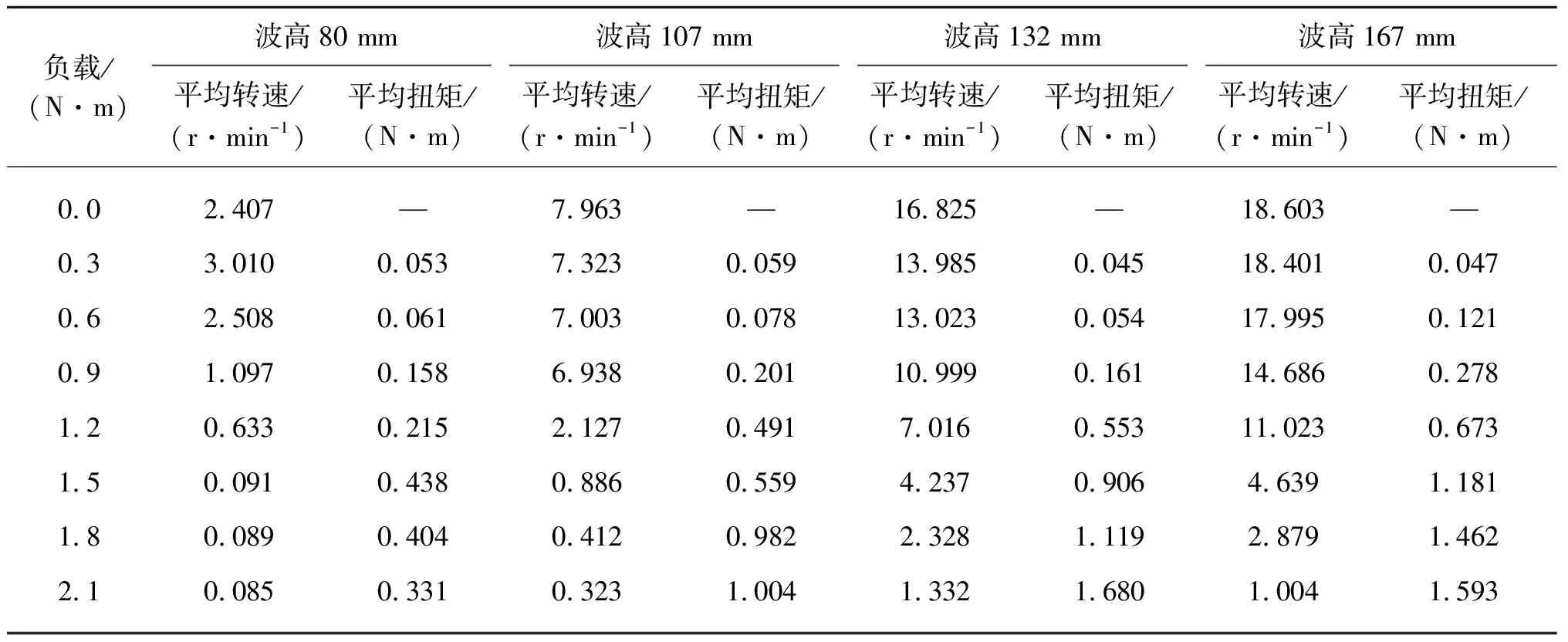
表7 波浪周期2.0 s测得桨叶平均转速和平均扭矩

对桨叶的功率进行计算，结果如图9所示。不同波浪条件下，功率曲线随负载逐渐增大呈先上升后下降的变化趋势。1.3 s和1.6 s波浪周期条件下除去曲线两端功率的较小值，随着负载变化，桨叶的功率基本大于5 W，桨叶捕能效果相对较好，2.0 s波浪周期条件下桨叶功率少有超过5 W，其捕能效果较差。根据图示曲线可知同一波浪周期条件下，若负载不变，波高越高桨叶所能达到的功率越大。1.3 s波浪周期条件下，桨叶处于1.5～1.8 N·m负载区间可达到最佳捕能效果，桨叶捕获功率最大可达到16 W；1.6 s波浪周期条件下，桨叶处于1.4～1.6 N·m负载区间可达到最佳捕能效果，桨叶捕获功率最大可达到23 W；2.0 s波浪周期条件下，桨叶捕能的最大功率为7.6 W左右，各条功率曲线变化趋势各有不同，总体没有明显的最佳负载区间，桨叶功率随负载变化的幅度不大，与1.3 s和1.6 s波浪周期差别明显。

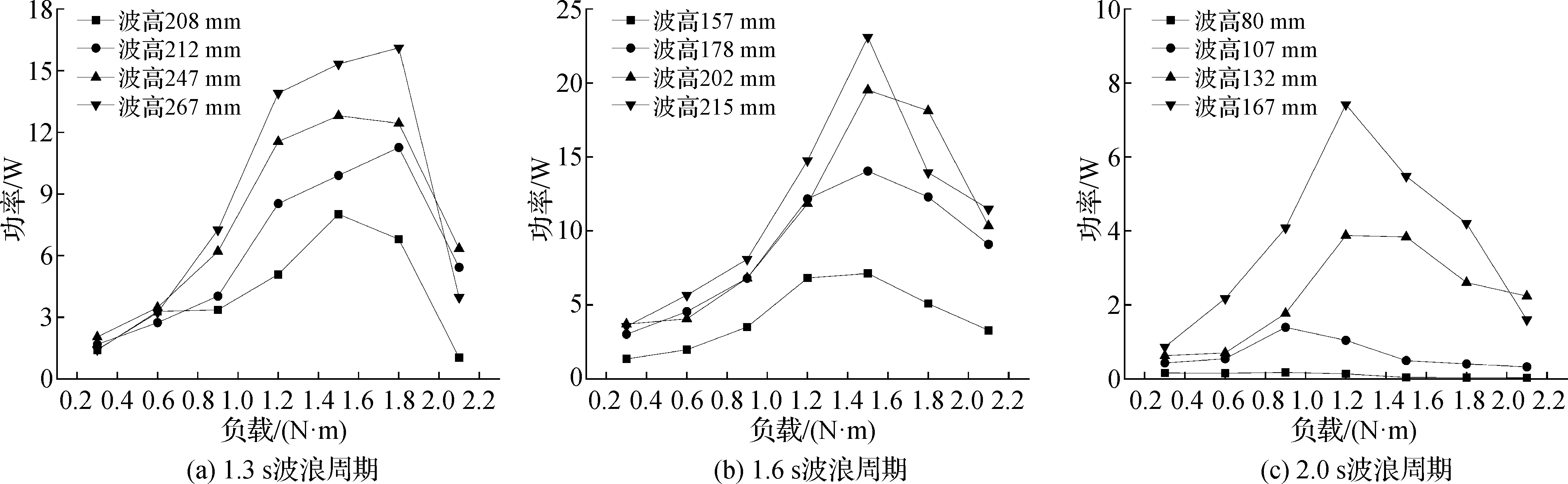
图9 桨叶功率随负载变化

3 总结与分析

相对旋转频率表示为桨叶旋转频率与波浪频率的比值，一定程度反应了桨叶的转动快慢，如图10所示，分别表示波浪周期1.3 s、1.6 s以及2.0 s下4种不同波高条件下的相对旋转频率。随着负载的增加，桨叶转动性能下降，符合桨叶转动的一般规律。相对旋转频率两端曲线变化较慢，中间段呈现显著下降趋势，在1.3 s 周期为负载0.9～1.5 N·m段，在1.6 s周期为负载1.2～1.8 N·m段，在2.0 s周期为负载0.9～1.5 N·m 段。对应图8可知桨叶最大功率在该区段产生。相比于1.3 s和1.6 s的短周期波浪，2.0 s长周期波浪条件下，桨叶应对不断加大的负载，其维持相对高转速的能力较弱，且转速更低。由对比结果可知该桨叶在1.3 s和1.6 s周期波浪条件下，拥有较好的运动性能。

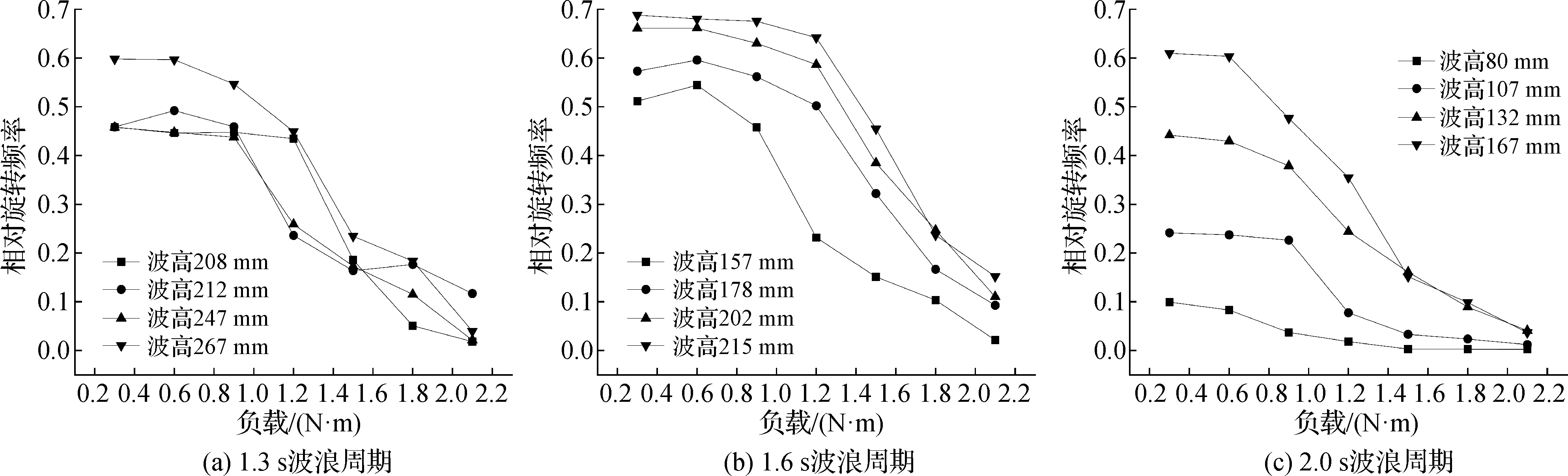
图10 桨叶相对旋转频率随负载变化

扭矩系数表示为桨叶实际产生的扭矩和理论上可获得的最大扭矩的比值，是评价桨叶性能的重要指标之一。如图11所示，分别表示波浪周期1.3 s、1.6 s以及2.0 s下4种不同波高条件下的桨叶扭矩系数。在1.3 s和1.6 s周期时，桨叶扭矩系数随着负载增加而增加，扭矩输出能力逐渐增强，符合一般研究规律。在长周期2.0 s时，相比其他2个周期，桨叶扭矩系数值整体较小，随着负载增加，系数曲线甚至出现先上升后下降再上升的波动现象，可知此条件下桨叶的力矩输出不稳定。1.6 s波浪周期条件下，各系数曲线变化趋势接近，可知此条件下桨叶产生的扭矩稳定均匀，拥有良好的转动性能。

图11 桨叶扭矩系数随负载变化

能量转换效率是指桨叶实际产生的能量和其从波浪中获取所得能量的比值，在Savonius型桨叶关于波浪能研究中直观表现了桨叶捕获能量的能力，是衡量桨叶性能优劣的一个重要指标，用η表示[8]：

(9)

式中：Ps表示桨叶实际产生的功率；Pw表示桨叶从波浪中获得的功率；τ表示桨叶扭矩；ρ表示水的密度；g表示重力加速度；H表示波高；T表示波浪周期。

如图12所示，分别表示波浪周期1.3 s、1.6 s以及2.0 s，4种不同波高条件下的桨叶功率系数随负载变化的曲线。可知功率系数先升高后降低，1.3 s和1.6 s波浪周期条件下，于负载1.5～1.8 N·m区间内出现最大值，最大值为0.16；2.0 s波浪周期条件下，于负载1.2～1.5 N·m区间内出现最大值，最大值为0.09。最大值所对应的负载区间与功率最大值对应的负载区间基本吻合。2.0 s长周期波浪条件下，桨叶的捕能效果较差；短周期波浪条件下，1.6 s周期时，桨叶在大负载下仍具有相对好的捕能效果。

图12 桨叶能量转换效率随负载变化

对桨叶的转动频率进行整理分析，在位于最大功率处，提取可有效捕能的点进行列表，如表8所示，可知桨叶最佳转动频率约位于0.14～0.25 Hz之间，可为实际应用中桨叶的选型和功率适配提供参考。

表8 桨叶转动频率对比

桨叶捕获的功率呈现先上升后下降的趋势，符合大部分学者对于Savonius型桨叶捕能性能的试验结果。同时可知对于低负载桨叶，因转矩过小无法带动有效载荷，其基本不具备将捕获能量进行有效转化的能力。

桨叶在2.0 s长周期波浪环境下，捕能及转化效果一般。在文中试验条件下最合适的波浪周期为1.6 s，最大功率可达到23 W。

4 结 语

文中试验采用数值仿真结合物理试验的方式，使用StarCCM+软件建立数值仿真模型，对桨叶进行带负载的波浪运动模拟试验，再对一个Savonius型水轮机加入负载装置，通过改变电流调整负载大小，并借助水池推板制造产生不同周期波高的波浪，进行相关的运动试验，记录并分析所采集数据，经过试验的综合比较，得到如下的结论：

1)对于不同波浪条件下带负载的二级Savonius型桨叶进行了性能测试，发现在波浪周期1.6 s时达到最佳捕能效果，桨叶所承载荷为1.5 N·m，最大功率可达23 W。

2)对于不同波浪，根据试验，当桨叶转动频率位于0.14～0.25 Hz间，可达到当前条件下的最佳捕能效果。

3)不同波浪条件下，随着负载增加，桨叶转速从快到慢变化，过程中数值会在某一负载区间出现明显跳跃，变化幅度较大，该区间正对应桨叶最大功率所在的负载区间。

4)不同尺寸型号的二级Savonius型桨叶，在带负载情况下会呈现不同捕能效果，有进一步研究价值。