一种求倒数近似值的量子算法及其量子电路
2022-04-02朱家良
朱家良,叶 宾,季 雯
(中国矿业大学 信息与控制工程学院,江苏 徐州 221116)
0 引 言
量子计算以其独特的并行计算特性,在机器学习、高维数据挖掘、大数据处理、图像处理等领域有着巨大优势[1-4]。和传统的数字计算相比较,量子计算显著减少了执行时间和能耗[5]。量子计算机的基本存储单元是量子比特,一个量子比特可表示量子态|0〉和|1〉的叠加,因此一次运算就可同时处理两个基态。处理2n状态的信息,n个量子比特仅需一次操作,远快于2n个经典比特所需的2n次操作[6]。正因如此,量子计算能够指数级加速传统算法,被认为是解决算力不足的有效方法之一。
求取一个无符号数的倒数在求解量子线性系统、量子相位估计、量子支持向量机等领域有着广泛的应用。在传统算法中常用牛顿迭代法、割线法等求取倒数的近似值,但是需要多次的迭代计算。量子计算的特性可以显著降低牛顿迭代计算的问题规模。Cao[7]于2007年首次提出了一种基于牛顿迭代法近似求取正整数倒数的量子线路,但其耗费辅助量子比特较多,线路结构复杂。该文提出一种更简洁的近似求取无符号数倒数的量子算法,此算法以基本的量子全加器[8-9]和量子乘法器[10-11]为基础模块,通过少量辅助寄存器进行连接,经过移位操作等搭建出量子电路。经过分析,其时间复杂度为O(n3),空间复杂度为O(2n3),具有量子代价小、结构简单等特点,有利于降低构造量子电路的成本及物理实现难度。
1 量子逻辑门基础
量子计算中的基本单位量子比特(qubit)与经典计算机中的比特(bit)相对应,单量子比特的状态为2个基态相叠加的形式[12]:|φ〉=α|0〉+β|1〉,其中α和β均为复数,满足|α|2+|β|2=1。
与经典计算机中的逻辑门类似,量子计算中的计算单元由量子逻辑门组成,它们在数学上是一个幺正变换和酉变换,并且这个变换是可逆的,在此介绍几种常用的量子逻辑门:
非(NOT)门,是一个单量子门,量子电路符号如图1(a)所示,它的作用是实现量子态从|0〉向|1〉的翻转。
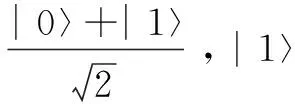
受控非(CNOT)门[13],是一个双量子逻辑门,由控制位和目标位组成。如图1(c)所示,它的作用是若控制位的量子态为|0〉,则目标位上的量子态不发生翻转;反之,若控制位量子态为|1〉,目标位上的量子态发生翻转。
Toffoli门[14],是一个三量子比特门,由两个控制位和一个目标位组成。如图1(d)所示,仅当控制位|a〉和|b〉都为|1〉时,目标位|c〉中的状态发生翻转,否则不发生变化。
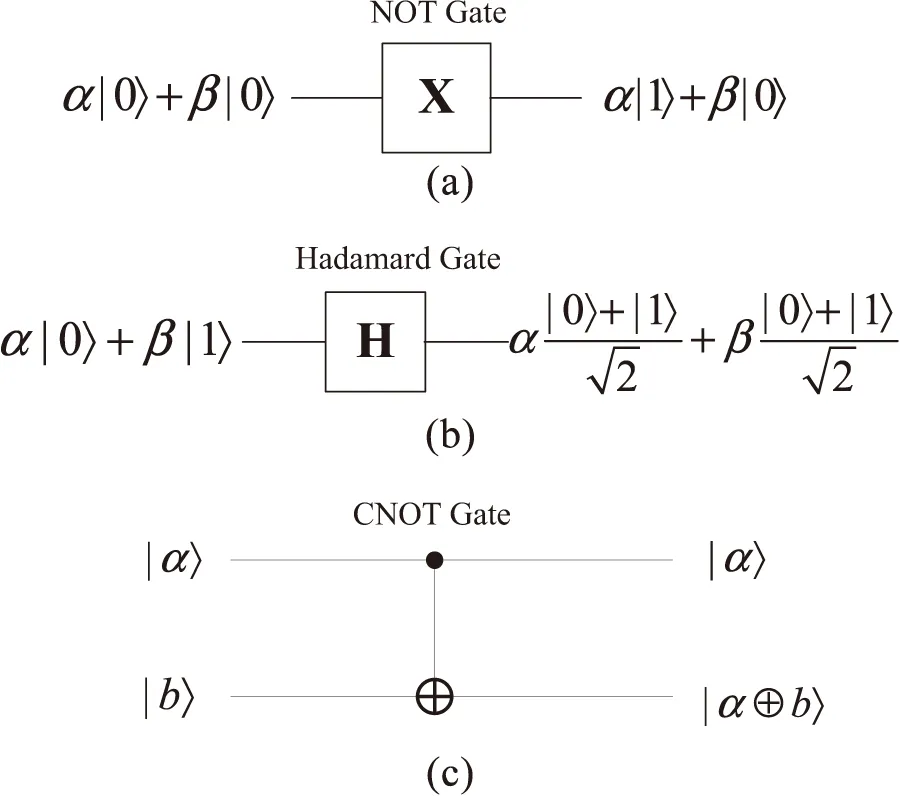
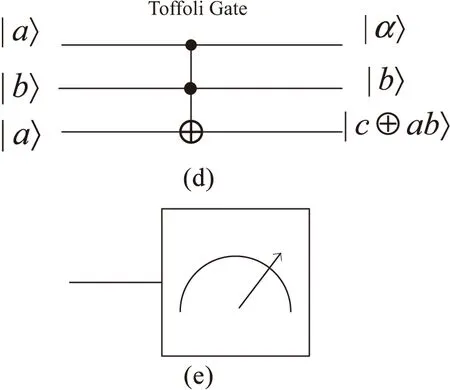
图1 量子逻辑门
测量门,将量子比特投影到经典比特中,实现观测。如图1(e)所示输入为处于叠加态的量子位,输出投影到|0〉和|1〉下的概率幅度。
2 量子乘法器的实现
2.1 量子半加器
n位的量子全加器是由n个半加器组成的,该文设计的半加器包括1个Toffoli门和2个CNOT门,如图2所示。其中|a〉和|b〉是输入的二进制数,|0〉是辅助量子位,结果存储在|sum〉中,|cout〉是进位。
半加器的过程如下:
|a〉|b〉|0〉|0〉→|a〉|b〉|sum〉|cout〉
(1)
辅助量子位输出:
|0〉|0〉→|sum〉|cout〉
(2)
|sum〉=|a⊕(b⊕0)〉
(3)
|cout〉=|ab⊕0〉
(4)
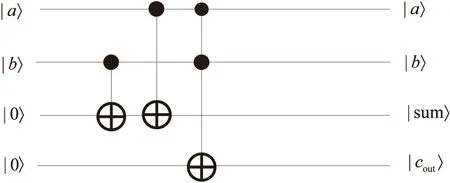
图2 量子半加器
2.2 n位量子全加器
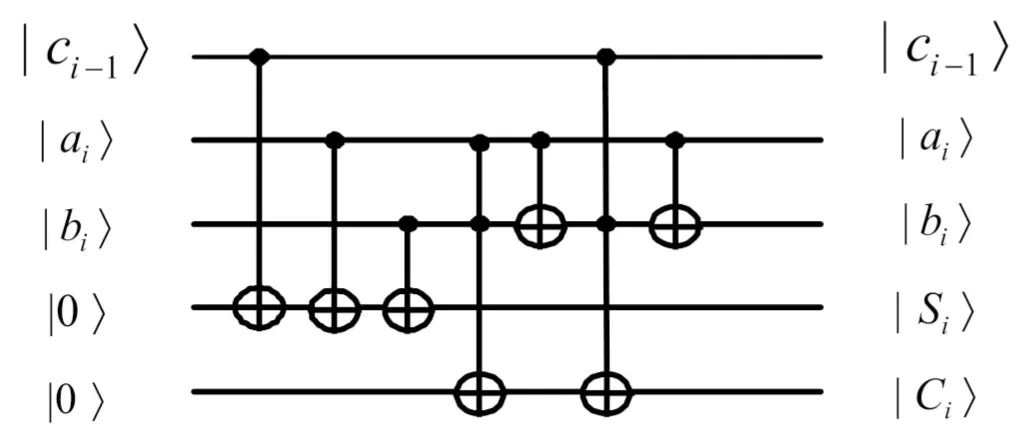
量子全加器是量子乘法器实现的基础。2002年,Cheng Kai-Wen[8]首次完善了量子全加器和量子全减器的电路图。常丽等人[9]于2019年采用了超前进位方式,简化了量子全加器的结构。在此基础上,该文根据全加器的逻辑表达式设计出单比特的量子全加器电路图,如图3(a)所示(图3(b)为其简化图)。然后将多个单比特的量子全加器组合,得到n比特量子全加器,如图3(c)所示。
|si〉=|ai⊕bi⊕ci-1〉
(5)
|ci〉=|aibi⊕(ai⊕bi)ci-1〉
(6)
其中,|ai〉是一个二进制数a的第i位,|bi〉是另一个二进制数b的第i位,|c〉是进位c的第i位,|si〉是a与b之和的第i位。
(a)单比特量子全加器电路图
(b)图(a)的简化图
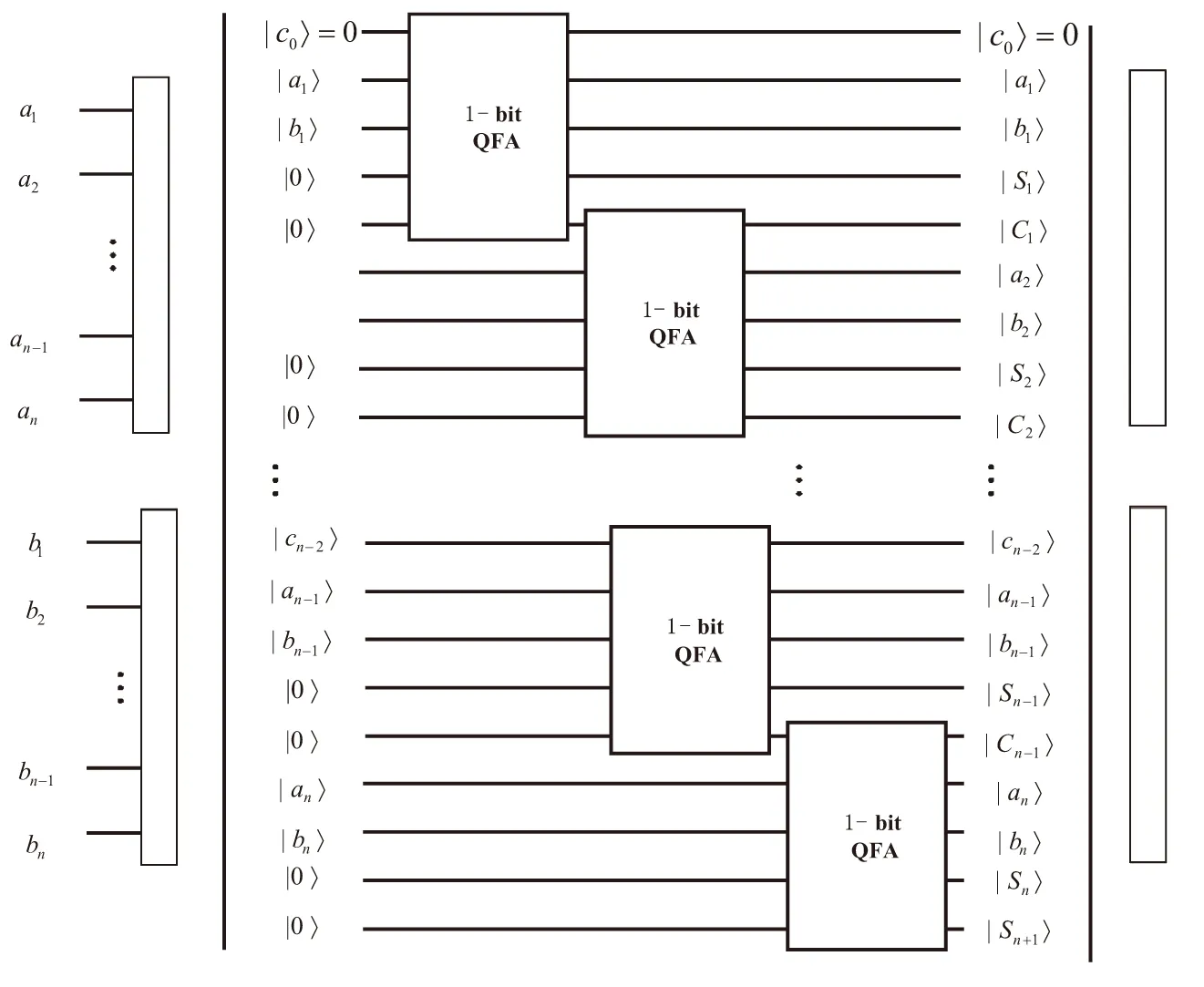
(c)n比特量子全加器电路图
2.3 量子乘法器
目前大多数的量子乘法器是在一个n量子比特的寄存器中输入|a〉1=|an-1〉1⊗|an-2〉1⊗…⊗|a0〉1来表示整数a=2n-1an-1+2n-2an-2+…+20a0;在另一个n量子比特的寄存器中输入|b〉2=|bm-1〉2⊗|bm-2〉2⊗…⊗|b0〉2来表示整数b=2m-1bm-1+2m-2bm-2+…+20b0;第三个l量子比特的寄存器用来存放前两个寄存器中的数相乘的结果,其状态为|c〉3=|cl-1〉3⊗ |cl-2〉3⊗…⊗|c0〉3,其中c=2l-1cl-1+ 2l-2cl-2+…+20c0。经过量子乘法器运算后各寄存器中的数值改变如下:
|a〉1|b〉2|c〉3→|a〉1|b〉2|c+abmod2l〉3
(7)
最后通过测量第三个量子寄存器,将其读数写入经典寄存器来得到两数相乘的结果[15-17]。
2.4 量子乘法器的移位实现
在实现量子乘法运算的过程中,最重要的一步就是对乘数进行移位相加,例如实现110和111的乘积,其实现步骤见图4(a)。由其规律可知,部分积之间的相加要实现左移操作,即在量子计算机上实现移位寄存器。文献[10]中设计的量子乘法器完善了移位寄存器的功能,算法整体的时间复杂度为o(n2),空间复杂度为o(n2)。Suzuki[11]在2020年提出的量子乘法器的时间复杂度和空间复杂度都较低,但是结构复杂。该文运用对寄存器低位置零的操作达到移位寄存器的效果,拥有结构简单、复杂度低等优点。具体步骤如下:
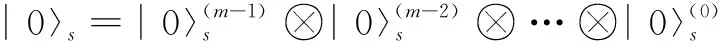
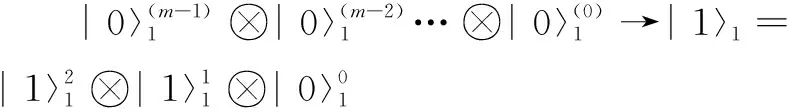
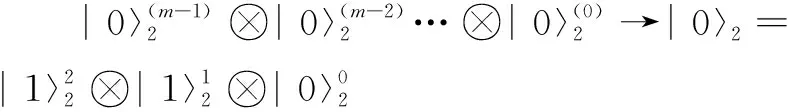
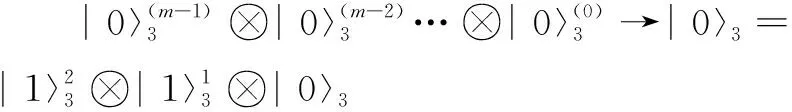
(8)
如图4(b)所示,将图4(a)中部分积的低位置零,再与高位相加,即可实现与移位同样的效果,110与111相乘的部分积低位置零后表示为:
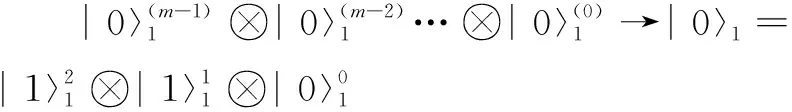
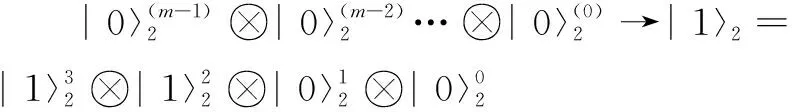
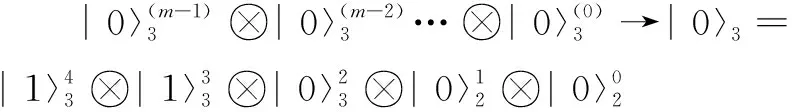
(9)
分析可知,此方法耗费寄存器的空间复杂度仅为O(2n-1)(n为两个乘数中位数较大的二进制数的位数)。

图4 置零乘法的实现步骤
2.5 量子乘法器的实现
下面按照图3(b)中所示的乘法计算过程,将输入寄存器、置零寄存器、全加器,以及输出寄存器(包含量子寄存器和经典寄存器)合并以设计出完整的量子乘法器。
如图5所示,输入寄存器中的n位二进制数|a〉1=|a〉1⊗|a〉2⊗…⊗|a〉n和m位二进制数|b〉2=|b〉1⊗|b〉2⊗…⊗|b〉m相乘,将部分积 |a0bt〉,|a1bt〉…|anbt〉,(t=0,1,…,m-1)的结果分别存放在置零寄存器:
|0〉0=|0〉0⊗…⊗|0〉t0⊗…⊗|0〉m-1(t0=0),
|0〉1=|0〉0⊗…⊗|0〉t1⊗…⊗|0〉m-1(t1=1)
⋮
|0〉l=|0〉0⊗…⊗|0〉tl⊗…⊗|0〉m-1(tl=n,l=2×max(n,m))上(第s个置零寄存器从第ts位开始存放,s=0,1,…,n);再将置零寄存器与全加器相连,依次求出部分积|0〉0,|0〉1,…,|0〉l的和(此过程中可以通过对|0〉s寄存器逐个清零来减少寄存器的使用,大大降低空间复杂度),并将结果存放在寄存器|c〉3=|c0〉3⊗…⊗|cl〉3中(l=2×max(n,m));最后通过测量将量子寄存器上的信息转化至经典寄存器c上,实现结果的观测。
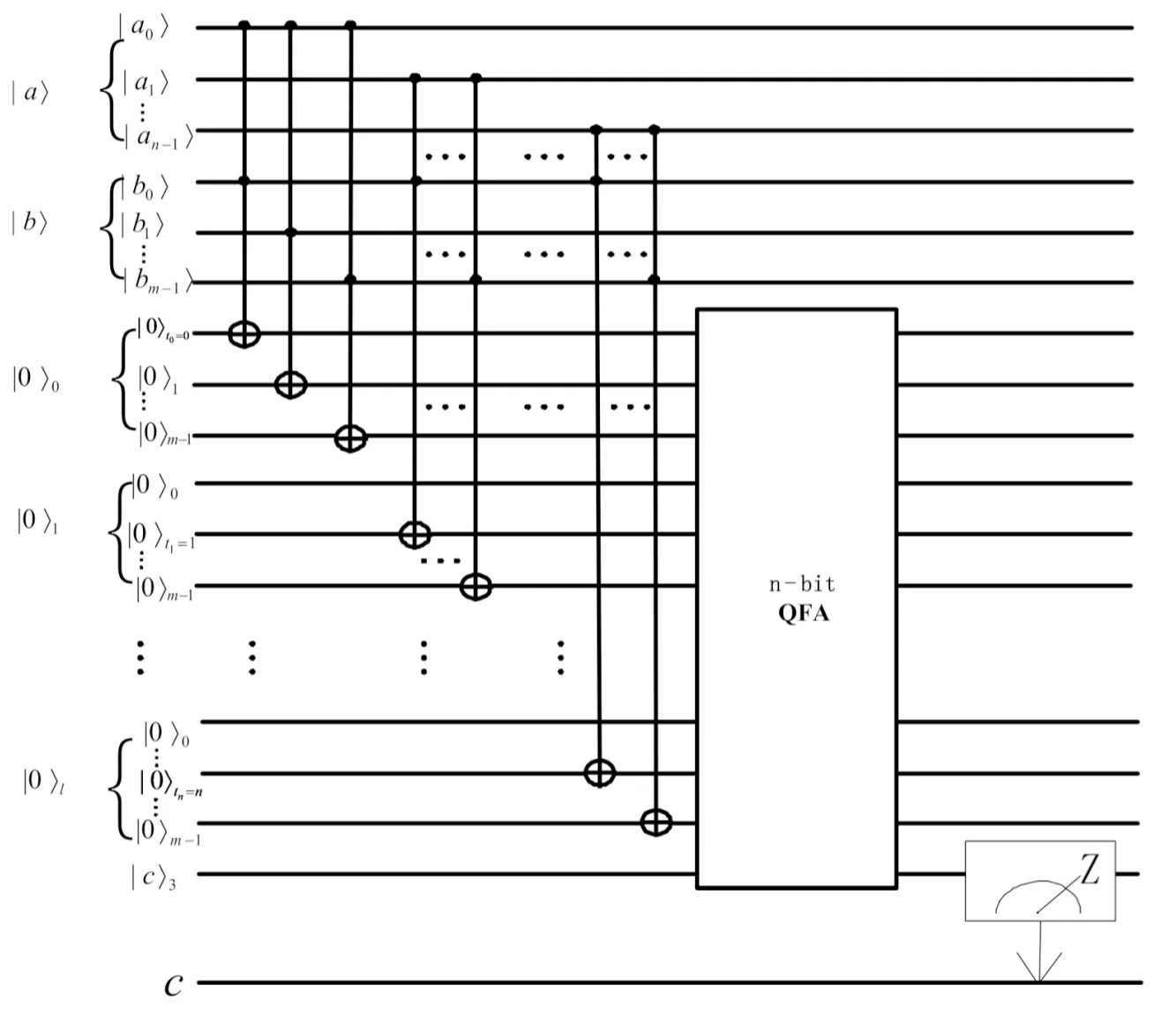
图5 量子乘法器电路图
2.6 量子乘法器复杂度分析
为了验证算法的有效性,该文用通用量子门作为时间单元,辅助量子比特作为空间单元,分析基于牛顿迭代法的量子倒数器的时间复杂度以及空间复杂度。
首先是时间复杂度的分析。对于n位二进制数乘以m位二进制数,该文改进的量子乘法器线路如图5所示。在量子乘法器中,首先是用Toffoli门进行各位二进制数的相乘操作,需要mn个Toffoli门。随后将辅助量子寄存器中的数进行相加,由图3(a)可知,一个比特的量子全加器由2个Toffoli和5个CNOT门组成,因此n比特的量子全加器需要7n个通用量子门。进行m次加法操作,因此需要用7mn个通用量子门。因此整个乘法器需要用到8mn个通用量子门,时间复杂度为O(mn)。若计算的二进制数都是n位,则时间复杂度为O(n2)。
其次是空间复杂度的分析。由图5所知,对于n位二进制数乘以m位二进制数(m>n),需要m+n个输入寄存器来储存输入的二进制数。一个辅助量子寄存器需要m个量子比特,m个辅助量子寄存器一共需要2m2量子比特。所以量子乘法器一共需要2m2+m+n个量子比特,时间复杂度为O(m2)。若计算的二进制数都是n位,则时间复杂度为O(n2)
该量子乘法器需要用到8mn个通用量子门,时间复杂度为O(n2)(m=n时)。所需量子寄存器的数量是2m2+m+n,空间复杂度为O(n2)(m=n时)。
3 求倒数近似值的量子算法及其量子电路
3.1 牛顿迭代法
根据牛顿迭代公式:
(10)
若求取已知数λ的倒数,则令函数f(x)为:
(11)
对f(x)求导得:
f(x)'=-x-2
(12)
联立式(6)~式(8)可得:
(13)
其中,λ为所求倒数的原数,要求满足λ>1;x0为满足x0>0且与λ-1相近的二进制数。图6为牛顿迭代法的电路图。
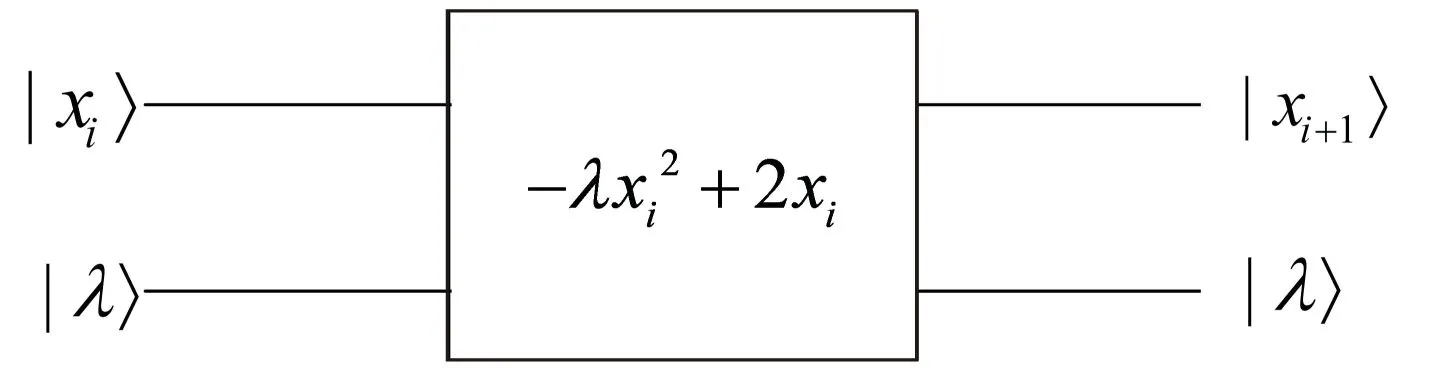
图6 利用牛顿迭代法求倒数的电路图
3.2 求倒数近似值的量子算法及其量子电路实现步骤
按照式(9)与图6的系统图,利用3个量子乘法器和2个量子全加器可设计出单步牛顿迭代法对应的量子电路,然后将每一步的迭代电路相连实现整个迭代过程。详细的迭代步骤如下:
(1)进行第一次迭代,将2和x0分别转化为二进制数,输入量子寄存器|a〉=|an-1〉⊗|an-2〉⊗…⊗|a0〉和|b〉=|bm-1〉⊗ |bm-2〉⊗…|b0〉中,把|2x0〉0的结果放入辅助寄存器|qcarry_sum0〉2n(n代表两个乘数中位数较多的二进制数的位数);
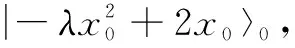
(3)通过测量将量子寄存器|qborrow〉上的信息转化至经典寄存器上,实现第一次迭代结果的观测。量子电路图如图7(a)所示;
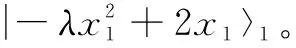
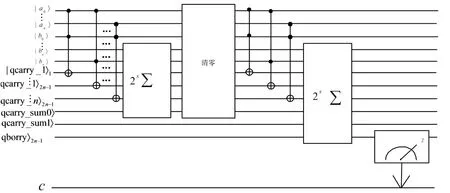
(a)一次迭代的倒数近似器电路
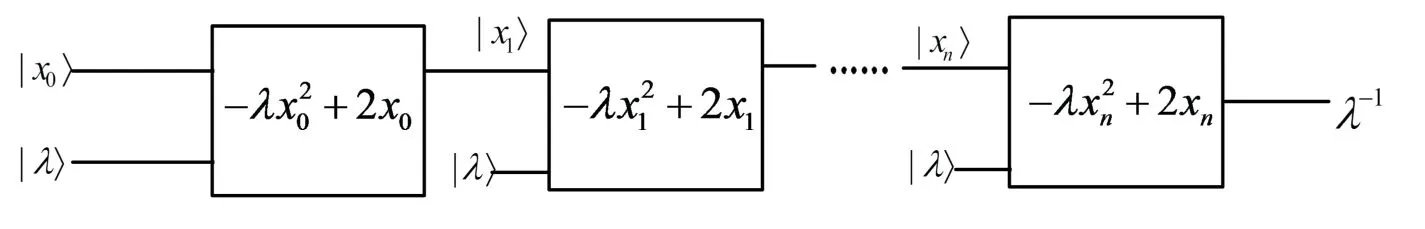
(b)n次迭代的倒数近似器电路
4 量子倒数器代价分析
4.1 时间复杂度
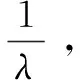
4.2 空间复杂度
由图7所示,λ与x0都为n位二进制数的时候,用以存放λ与x0的寄存器数量为2n,辅助寄存器|qcarry_1〉1至|qcarry_n〉2n-1的数量为2n2-n,寄存器|qcarry_sum0〉和|qcarry_sum1〉的数量一共为4n,寄存器|qbarrow〉的数量为2n-1,因此一共所需的寄存器为2n2+7n-1。最终一次迭代的倒数计算器的空间复杂度为O(n2)。用n个倒数器进行叠加相连,空间复杂度为O(n3)。
5 结束语
该文设计的基于牛顿迭代法的量子倒数计算器实现了求取n位二进制数的倒数,并且改进了量子乘法器,用低位置零操作代替移位操作。该设计大大降低了系统的空间复杂性。时间复杂性分析进一步表明,所设计的量子倒数器的时间复杂度并未远大于单独的乘法器,且结构简单,易于优化,迭代次数可根据具体精度需要任意选择。
