改进的支持向量机在心脏病预测中的研究

王成武，郭志恒，晏峻峰

(湖南中医药大学 信息科学与工程学院，湖南 长沙 410208)

0 引 言

心脏病是日常生活中一种比较常见的循环系统疾病。根据《中国心血管健康与疾病报告(2019)》，心血管病的死亡率在中国人群所有死亡原因中位居于榜首，农村居民心血管病占死因的45.91%，城市居民占43.56%[1]，它不仅会给患者的生活质量带来十分严重的影响，也给患者和国家带来了繁重的经济负担。

如何及时地预测出潜在心脏病患者并对其进行相应的诊疗具有十分重要的意义，但是传统的心脏病检测技术存在着各种各样的弊端，以至于心脏病的预测不能够很好的进行[2]。目前，支持向量机(support vector machines，SVM)在疾病诊断上的应用已经有了很多，例如吴辰文等人[3]提出一种改进的SVM算法应用在乳腺癌诊断方面，预测Random Forest模型下的基尼指数特征加权的支持向量机在乳腺癌诊断中的结果；张丽娜等人[4]提出一种基于支持向量机的急性出血性脑卒中早期预后模型的建立与评价，研究表明其效果优于逻辑回归，同时，肝病、红斑鳞状皮肤病及糖尿病等疾病[5-7]也都基于支持向量机建立了相应的疾病诊断模型，并且取得了非常好的实验效果，充分地表明了支持向量机(SVM)模型在当今疾病诊断领域的应用具有广阔的前景。

该文将利用SVM建立心脏病分类预测模型，并通过网格搜索对SVM的惩罚因子C和核参数g进行初步优化，缩小参数寻优范围，再使用粒子群优化算法PSO对SVM的惩罚因子C和核参数g进行优化，得到最优参数组合，从而提高SVM模型的分类准确率。

1 基本原理及方法

1.1 实验数据

实验中所选用的是UCI机器学习库里面的心脏病数据集。该数据集是由美国克利夫兰心脏病临床基金会提供的，包含心脏病检查患者的部分体质数据，一共有303个样本，其中阳性样本的个数是164，阴性样本的个数是139，数据集包含13个特征属性和1个类属性，分别是age(年龄)、sex(性别)、cp(胸痛类型)、trestbps(静息血压)、chol(血清胆汁)、fbs(空腹血糖)、restecg(静息心电图)、thalach(最大心率)、exang(运动性心绞痛)、oldpeak(运动引起的相对于休息的ST抑郁)、slope(最高运动ST段的斜率)、ca(萤光显色的主要血管数目)、thal(一种称为地中海贫血的血液疾病)、target(分类类别)。

1.2 基本原理

1.2.1 支持向量机

支持向量机是Cortes和Vapnik在1995年提出来的，它是在统计学理论的VC维(Vapnic-Chervonenkis Dimension)和结构风险最小原理基础上所提出的一种机器学习算法[8-10]。其最终目的是要在样本空间中找到一个最优的划分超平面，该平面产生的分类效果的鲁棒性和泛化能力是最优的。支持向量机算法具有很多独特的优势，在实验过程中通常可以获得比其他分类器更好的效果，在应对线性不可分问题的时候，可以采用带有诸如径向基核函数的支持向量机，这样可以扩大特征空间，从而解决非线性可分问题。

假设训练样本集D={(x1,y1),(x2,y2),…,(xn,yn)}，其中yi∈{-1,+1}分别表示健康人群和心脏病患者。在d维空间中，划分超平面对应模型可表示为：

f(x)=ωTφ(x)+b

(1)

式中，φ(x)表示将x映射后的特征空间，ω和b是模型的参数。由软间隔最大化可得原始最优分类问题为：

(2)

式中，ξi为松弛变量，C为惩罚因子。式(2)本身是一个凸二次规划问题[11]，引入拉格朗日函数：

(3)

式中，αi,μi是拉格朗日乘子。

原始问题转换为对应的对偶问题：

(4)

求解式(4)可得模型为：

(5)

SVM常用的核函数有以下几种：

线性核函数：

K(xi,xj)=xixj

(6)

多项式核函数：

K(xi,xj)=(xixj+1)d

(7)

径向基核函数：

(8)

拉普拉斯核函数：

(9)

Sigmoid核函数：

K(xi,xj)=tanh[β(xixj-θ)]

(10)

该文选择径向基核函数(RBF)。

1.2.2 粒子群优化算法

粒子群优化算法(particle swarm optimization，PSO)是Eberhart和Kennedy于1995年推出，它是以鸟群捕食行为为来源而产生的[12-13]，属于一种进化算法。根据搜索过程中群体的消息共享进行更新，使得整个群体向着最优解的方向移动。粒子群中的每个粒子都代表优化问题所对应的一个可能的解，假设在d维空间中有一群粒子，粒子的位置表示为：

Xi=(Xi1,Xi2,…,XiD)

(11)

粒子的速度表示为：

Vi=(Vi1,Vi2,…,ViD)

(12)

粒子的位置和速度更新公式如下：

(14)

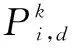
1.2.3 PSO-SVM模型

该文利用PSO算法对支持向量机的参数进行寻优,建立PSO-SVM算法模型，粒子群中的每个粒子由{C,g}组成，支持向量机参数选择的适应度函数使用K折交叉验证分类准确率。

基于PSO-SVM算法的心脏病预测步骤如下：

步骤1：初始化粒子群及参数。对粒子群规模m、局部搜索能力c1、全局搜索能力c2、最大进化数量k、惯性权重w、惩罚因子C的取值范围，核参数g的取值范围进行初始化；

步骤2：利用5折交叉验证来计算训练集分类准确率，以此作为当前种群中每个粒子的适应度值，得到最初的个体最优适应度值、全局最优适应度值和对应的参数(C,g)；

步骤3：每一次迭代中，利用式(13)和式(14)更新粒子的位置和速度；

步骤4：使用适应度函数对粒子群中所有粒子的适应度值进行计算；

步骤5：将粒子的适应度函数值及其出现过的最优适应度值进行比较,若更优，则更新个体最优适应度值,以便于下一次迭代过程的比较；

步骤6：将粒子的适应度值和整个种群中出现过的最优适应度函数值进行比较,若更优，则对全局最优适应度值进行更新,以便于下一次迭代过程的比较；

步骤7：判断是否达到终止条件，如果达到就终止迭代，否则回到步骤3；

步骤8：得到SVM模型的最优参数组合(C,g)，对心脏病测试数据集进行预测，计算心脏病分类准确率。

2 实验过程与分析

网格搜索[14-15]进行SVM参数寻优是通过遍历以惩罚因子C和核参数g组成的二维网格，并采用K折交叉验证计算参数组合(C,g)下训练集的分类准确率，找出二维网格中准确率最高的点，即为参数优化的结果[16]。若参数所设定的取值范围很大，足以包含参数寻优的最优解，并且网格遍历的步长足够小，这样就能够找到全局最优参数组合，但是步长较小的话，对整个网格进行遍历就会耗费很多的时间。因此，先采用网格搜索在较大的参数取值范围内使用较大的步长进行粗略搜索，确定惩罚因子C和核参数g的大致范围，然后使用粒子群优化算法PSO在较小取值范围内对参数组合进行进一步的精确搜索，得到最优参数组合。

该心脏病预测模型的运行环境是Windows系统下的MATLAB R2020a平台。抽取70%的心脏病数据集作为训练集，剩下的30%作为测试集，根据测试集分类结果对模型进行评价。实验一共包含两个部分：实验1，利用网格搜索与交叉验证对SVM的惩罚因子C和核参数g进行优化选择，确定最优参数的粗略范围；实验2，在实验1的基础上，利用PSO算法对支持向量机的参数C和g进行进一步的寻优，计算测试数据集的分类准确率。

2.1 数据预处理

数据集共有13个特征属性，其中age,trestbpd,chol,thalach,oldpeak为数值型，sex,fbs,exang,target为二值型，cp,restecg,slope,ca，thal为多分类数值，例如胸痛类型包含四个值(0:典型心绞痛，1:非典型心绞痛，2:非心绞痛，3:无症状),使用one-hot编码[17]对多分类数值进行处理，编码过程如图1所示。

为规避不同变量之间的量纲差异，提高支持向量机(SVM)模型的预测效果，将样本数据集进行归一化处理，归一化公式为：

(15)

令ymin为0，ymax为1，使得最终的数据都落在 [0,1]区间内，得：

(16)

2.2 网格搜索优化SVM参数

通过网格搜索与交叉验证相结合的方法确定模型的参数C和g。具体步骤如下：

步骤1：设定惩罚因子C和核参数g的大致取值范围分别是：C∈[2-10,210]，g∈[2-10,210]，步长设置为2，对C值为横坐标、g值为纵坐标的二维网格进行搜索；

步骤2：一个坐标点代表参数(C,g)的取值，利用5折交叉验证计算训练集的分类准确率，记录该准确率的值以及对应的参数取值，不断重复此步骤，直至遍历完整个网格；

步骤3：将分类准确率最高的点对应的参数(C,g)作为最优参数取值。

经过对二维网格的初步搜索，由图2可知，5折交叉验证最佳分类准确率CVAccuracy为87.559 8%，其对应的最佳参数组合(C,g)分别为C=4，g=0.25。

2.3 PSO算法优化SVM参数

通过网格搜索进行参数的初步寻优后，将参数的取值范围缩小，在本次实验中，PSO优化算法的参数设置为：粒子群数量N=20，惯性权重ω=0.7，参数局部搜索因子c1=1.49，参数全局搜索因子c2=1.49，最大迭代次数Kmax=100，惩罚因子C∈[0.1,30]，核函数参数g∈[0.1,30]。利用5折交叉验证计算心脏病训练集分类准确率的平均值，并记录与此对应的参数组合(C,g)，根据最终的分类结果选出模型最优的参数组合。

优化结果如图3所示。

由图3可知，随着迭代次数的增加，群体中最佳个体适应度(即分类准确率)增加至89%左右，并基本保持不变，其对应的最优参数组合(C,g)分别为C=0.771 15，g=0.1。

2.4 模型结果分析

模型的评估指标有很多，由于该文是关于疾病分类预测的研究，所以选用准确率、灵敏度和特异度作为模型的评估指标，三个指标的计算公式如下：

(17)

(18)

(19)

其中，真正例TP为测试集中阳性样本预测结果也是阳性的个数；伪反例FN为测试集中阳性样本预测为阴性的个数；伪正例FP为测试集中阴性样本预测为阳性的个数；真反例TN为测试集中阴性样本预测结果也是阴性的个数；Acc为测试集的分类准确率；Sen为灵敏度，代表识别真阳性的能力;Spec为特异度，代表排除真阴性的能力。对比经过网格参数寻优、粒子群优化算法(PSO)寻优后的SVM模型和原始SVM模型，原始模型随机选取的参数为C=1，g=1，结果如表1所示。

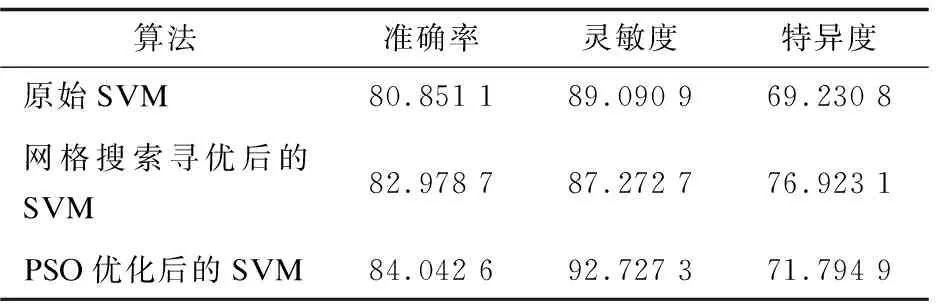
表1 SVM分类模型结果对比 %

通过对最终实验结果的比较可以看出，未经优化的模型的惩罚因子C和核参数g按照人为的经验进行设置，在测试集上的分类准确率为80.851 1%，经网格搜索和交叉验证相结合的方法对参数进行初步的优化，得到最佳参数组合C=4，g=0.25，此时分类准确率提升到82.978 7%，在此基础上，缩小参数优化范围，使用PSO对SVM参数再次进行优化，得到的最佳参数组合为C=0.771 15，g=0.1，分类准确率进一步提升到84.042 6%，如图4～图6所示。

同时，灵敏度和特异度也得到提升，支持向量机模型在测试集上的灵敏度从89.090 9%提升到了92.727 3%，特异度也从69.230 8%提升到71.794 9%，可见经优化后模型的效果得到了提高。

2.5 优化的SVM与其他分类模型的比较

K-最近邻算法(KNN)、线性判别分析(LDA)和分类与回归树(CART)在分类预测中的应用较多，选用这三种常用的机器学习算法来构建心脏病分类预测模型，将其分类结果与经过参数寻优后支持向量机在测试集上预测的结果进行比较分析。结果如表2所示，CART分类准确率最差，KNN和线性判别分析的分类准确率和CART相比有所提高，分类准确率最高的为文中进行参数优化后的支持向量机。

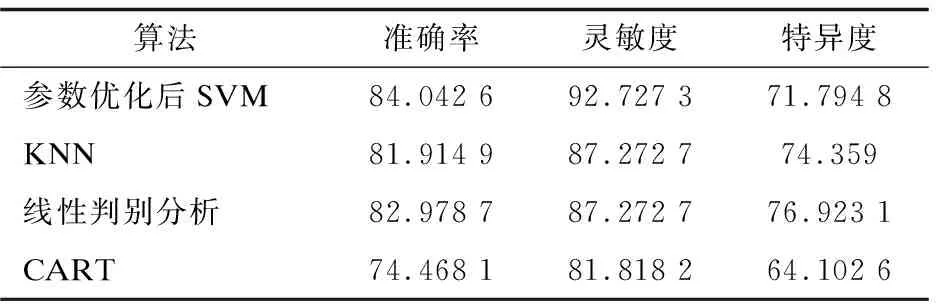
表2 优化的SVM与其他分类模型结果对比 %

3 结束语

选取UCI机器学习库中的心脏病数据集，建立了基于SVM的心脏病预测模型，可以为医生在心脏病辅助诊断中提供一定的帮助。首先结合网格搜索与交叉验证对模型的最优参数组合进行初步寻优，接着缩小参数范围，利用粒子群优化算法进行参数寻优，确定模型的最优惩罚因子C和核参数g。与基于传统SVM建立的心脏病预测模型相比，参数优化后的SVM的准确率、灵敏度和特异度都得到了提升，验证了实验的有效性。