基于多元线性回归的学生成绩预测研究
2022-04-02刘晓雲刘鸿雁李劲松王冠帮
刘晓雲,刘鸿雁,李劲松,王冠帮
(1.渤海大学 教育科学学院,辽宁 锦州 121000;
2.渤海大学 信息科学与技术学院,辽宁 锦州 121000)
0 引 言
随着中国经济的快速发展,人才需求越来越大,教育也越来越受到社会的关注。为了保证教学质量,国家也不断颁布新的教育整改政策,数据挖掘技术也逐渐深入地应用到了教育领域,例如关联规则、多元线性回归、聚类分析、分类预测等等。其中成绩预测可以督促学生,使学生及时调整自己的学习方法,改变学习策略,并且使教师及时改进教学策略,所以成绩预测是提升学生成绩的重要手段。它也成为了教育数据挖掘领域的一个热点研究课题[1]。
对学习成绩进行预测分析对提高教学质量有着十分重要的作用,一些国内外学者对此已经开展了相关研究。尤佳鑫利用多元线性回归方法,预测了云环境下的学生学业成绩[2]。徐铭希采用多种机器学习算法对学生成绩进行预测并构建最优模型[3]。赵光等人利用多元线性回归方法,构建大学英语四级考试成绩预测模型[4]。张晓等人通过多元线性回归,分析了基础课程对专业课程的影响[5]。汪慧利用多元线性回归方法,建立通过影响电子技术的6门课的成绩预测该门课的模型[6]。虽然国内外学者已经开展相关的成绩预测研究,但多是利用现有全部成绩预测某科成绩。利用一年级预测毕业成绩较少,未能充分发挥成绩预测的及时性。
目前普遍认为,一个人的学习成绩是符合一定趋势的,并且一年级时期开展的课程,包括基础课和通识课,对毕业总体成绩也有着一定的影响。其中如解析几何这样的专业基础课程,对后面其他专业课的学习有着直接的影响。因此利用一年级预测毕业成绩具有可行性和可预测性。
回归分析是研究统计规律的方法之一。应用回归分析评价考试成绩不仅能分析各种因素对考试成绩的影响大小,还能对成绩进行合理的预测[7-8]。鉴于多元回归分析的以上优点,所以建立多元回归模型不仅可以帮助教师改进教学方法,还可以帮助学生及时调整自己的学习方法,以便得到更好的成绩,为提高教学质量提供了保障。
1 回归分析
1.1 线性回归
线性回归有很多实际用途。分为以下两大类:如果目标是预测或者映射,线性回归可以用来对观测数据集的和X的值拟合出一个预测模型。当完成这样一个模型以后,对于一个新增的X值,在没有给定与它相配对的y的情况下,可以用这个拟合过的模型预测出一个y值。
给定一个变量y和一些变量X1,X2,…,Xp,这些变量有可能与y相关,线性回归分析可以用来量化y与X之间相关性的强度,评估出与y不相关的X,并识别出哪些X时子集包含了关于y的冗余信息。
1.2 多元线性回归
多元回归分析是指在相关变量中,将一个变量视为因变量,其他一个或多个变量视为自变量,建立多个变量之间线性或非线性的数学模型数量关系式,并利用样本数据进行分析的统计分析方法。另外,也要讨论多个自变量与多个因变量的线性依赖关系的多元回归分析,称为多元多重回归分析模型。通常影响因变量的因素有多个,这种多个自变量影响一个因变量的问题,可以通过多元回归分析来解决。在线性回归分析中,多元线性回归比一元线性回归具有更大的实用意义[9-10]。
多元线性回归分析的基本任务如下:根据因变量与众多自变量的实际观察值建立因变量对多个自变量的多元线性回归方程;评定各个自变量对因变量影响的相对重要性以及测定最优多元线性回归线性方程的偏高度等[11-13]。许多多元非线性回归问题可以通过多元线性回归来解决,所以多元线性回归具有广泛的应用。
1.3 多元线性回归模型
设变量Y与变量X1,X2,…,Xp间有如下的线性关系:
Y=β0+β1X1+…+βpXp+ε
(1)
其中,β0是回归常数,β1,β2,…,βp是总体回归参数,当p=1时,称公式(1)为一元线性回归模型,p≥2时,称之为多元线性回归模型。ε为随机误差,且服从ε~N(0,σ2)分布。
参数β的估计方法最常用的是最小二乘估计法(ordinary least square,OLS),其目标函数为最小化:
(2)
因在解决实际问题时,矩阵X'X通常都是奇异的。所以当X'X是非奇异矩阵时,表明变量之间不完全相关,而这时得到的最小二乘估计为:
(3)
从而可得回归模型为:
(4)
1.4 多元线性回归模型的检验
由建立的多元线性回归模型以及已得到的回归系数,要对整个回归方程进行拟合检验,可以采用R2检验。
判定系数R2的定义为:
(5)
其中,SSR表示回归平方和,其定义如公式(6),反映了由于x与y之间的线性关系引起的y的变化部分;SST表示总离差平方和,其定义如公式(7),反映因变量的n个观察值与其均值的总离差;SSE表示残差平方和,其公式如公式(8),反映除了x对y的线性影响之外的其他因素对y变差的作用,是不能由回归直线来解释的y的变差部分。
(6)
(7)
(8)
三者之间的关系满足:
SST=SSR+SSE
(9)
R2反映的是回归直线对数据的拟合优度,取值在[0,1]之间。R2趋近于1,说明回归方程拟合得越好,相反,R2趋近于0,说明回归方程拟合得越差。
2 基于多元线性回归的学生成绩预测研究
鉴于SPSS软件是目前教育研究领域使用最为广泛的统计软件之一,具有界面美观、操作简洁的特点,因此该文在实验数据处理中使用了SPSS软件[14],用其对实验数据进行单次实验。而预处理和统计分析部分基于Matlab系统完成。
2.1 数据预处理
2.1.1 数据收集
实验数据选用某学校计算机应用专业一年级共55名学生的课程成绩。由于部分课程涉及分流培养,因此实验数据仅使用17门课程。
2.1.2 数据处理
(1)为保护学生隐私,将原始学生姓名用编号替代以及将性别、学号等身份信息隐藏,只保留所需的成绩、课程名称等基本信息。
(2)为了使数据结果更具有合理性、普遍性,除去极端学生成绩的影响,因此去掉低于平均成绩大于X+3σ或小于X-3σ的学生,最后剩下53名学生的课程成绩。
(3)实验数据中的部分课程成绩采用等级制进行的赋分(优秀、良好、中等、及格、不及格),对这类数据前期进行了转换和处理,转换原则为“优秀”对应95分,“良好”对应85分,“中等”对应75分,“及格”对应65分,“不及格”对应59分。
(4)为避免数据属性的影响,对所有实验数据都进行了归一化[0,1]处理,最终获得的部分实验数据如表1所示。
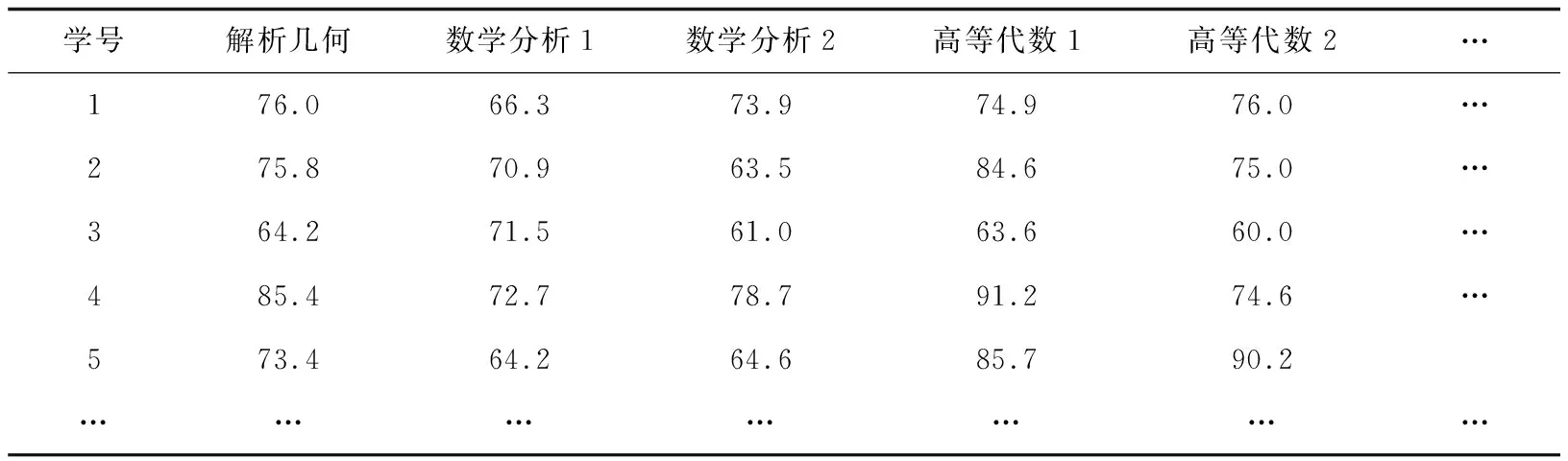
表1 部分学生成绩
2.2 建立多元线性回归模型及其分析
2.2.1 实验原理与结果
中国旅游业的发展经历了从单一入境旅游市场,到入境旅游、国内旅游两个市场并举,再到入境旅游、国内旅游、出境旅游三个市场全面发展的过程[4]。与此相应,我国旅游业三大市场发展战略也经历一系列的调整变化,现定位为“全面发展国内旅游、积极发展入境旅游、规范发展出境旅游”[4]。
平均绝对误差(mean absolute error,MAE)是所有单个观测值与算术平均值的偏差的绝对值的平均,所以选用简便、直观的平均绝对误差作为评估成绩预测模型的预测误差指标[15],其计算公式如下所示。
(10)
其中,N为样本个数;Score和Scorep分别为原始成绩和模型预测成绩。MAE值越小,模型预测误差越小,预测越准确。
该文随机从53名学生中选出3名、5名、10名和20名作为测试样本(训练样本数量即为50名、48名、43名和33名),并分别进行100次随机选择。然后对得到的MAE值取其平均值,得到的最终平均预测性能结果如表2所示。
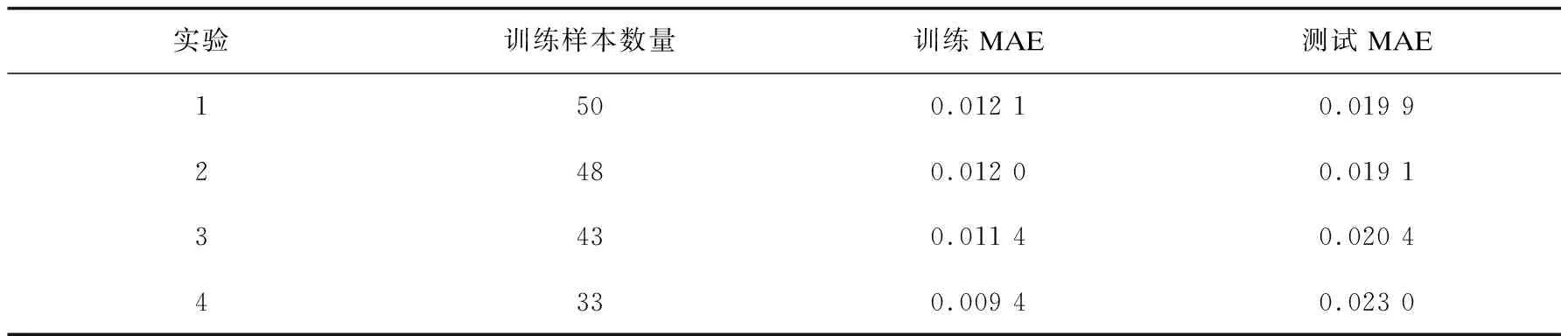
表2 训练和测试样本MAE详情
统计结果表明,训练和测试误差都小于1.9%,说明构建的预测模型具有较高的预测精度,已证明利用一年级预测毕业成绩可行。此外,从表中也可看出构建的模型性能对训练样本需求较低,更利于推广。
2.2.2 单次实验结果分析
为了更加清楚地展现实验结果,分别选用上述四种实验的某一次实验结果进行具体分析。利用SPSS软件进行分析,令四年总体平均成绩为因变量,17门课程成绩为自变量。
(1)实验4。
(-0.014)X7+0.009X8+(-0.021)X9+0.025X10+(-0.005)X11+
0.085X12+0.192X13+0.140X14+0.290X15+0.092X16+(-0.108)X17
(11)

表3 模型摘要

表4 多元回归模型概要
对所建立的实验4的线性回归模型进行R2检验,从表3可以看出,R2的值为0.894,接近0.9,趋近于1,说明模型的拟合度很高。从表4可以看出,模型的准确性为97.3%(>95%),进一步说明模型的拟合度高。
通过模型预测出剩余20个测试样本的预测值,如表5所示。预测差值最高不超过3.5分,平均误差为1.43%,预测性能精度较高。
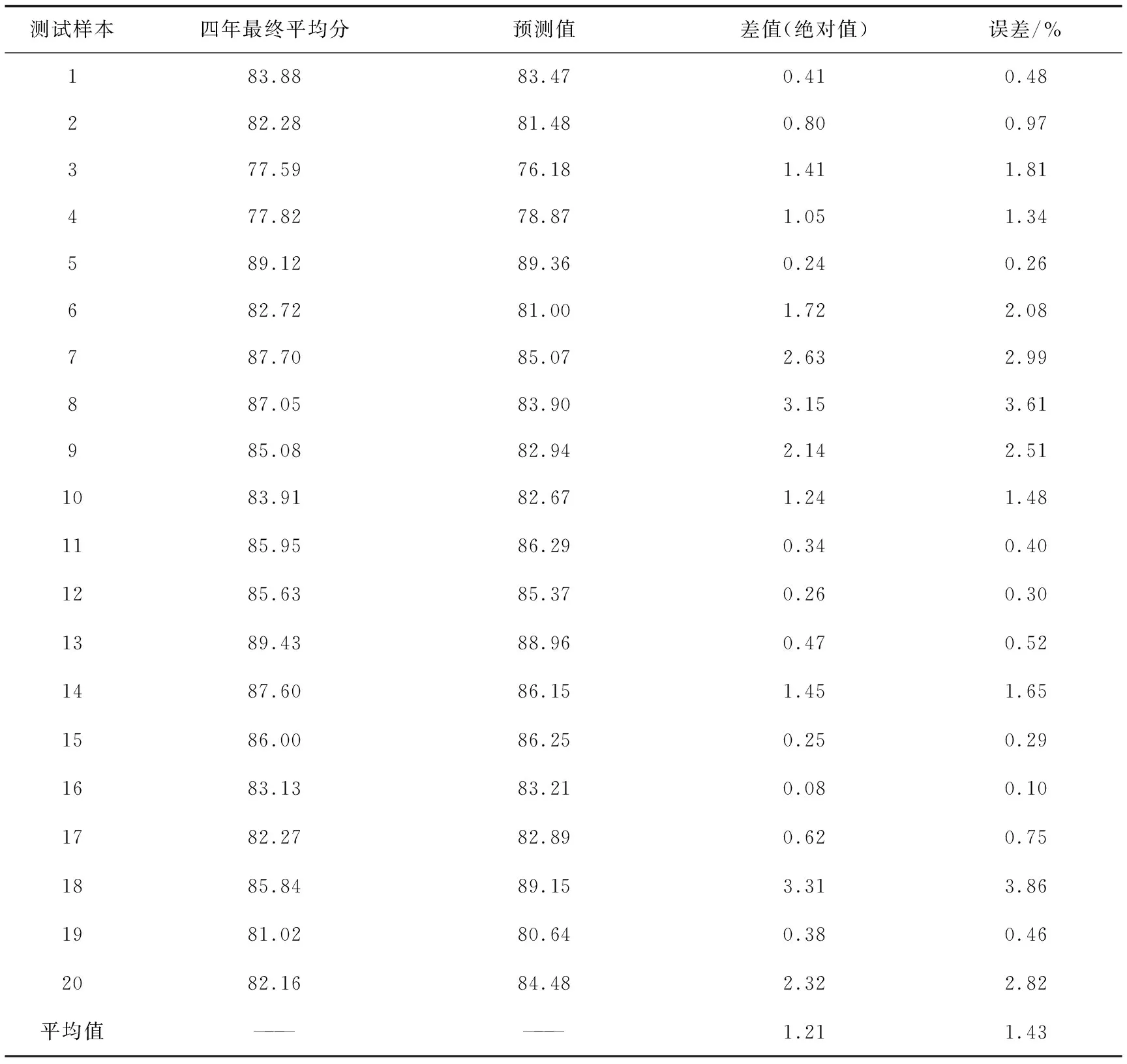
表5 实验4真实值和预测值对比
(2)实验3。
类似地,实验3的43个训练样本得到的标准线性回归方程为:
0.162X6+(-0.007)X7+(-0.014)X8+0.008X9+0.023X10+0.011X11+
0.092X12+0.163X13+0.079X14+0.264X15+0.127X16+(-0.073)X17
(12)
通过模型预测出剩余10个测试样本的预测值,如表6所示。预测差值最高不超过1.5分,平均误差为0.9% ,预测性能精度较高。
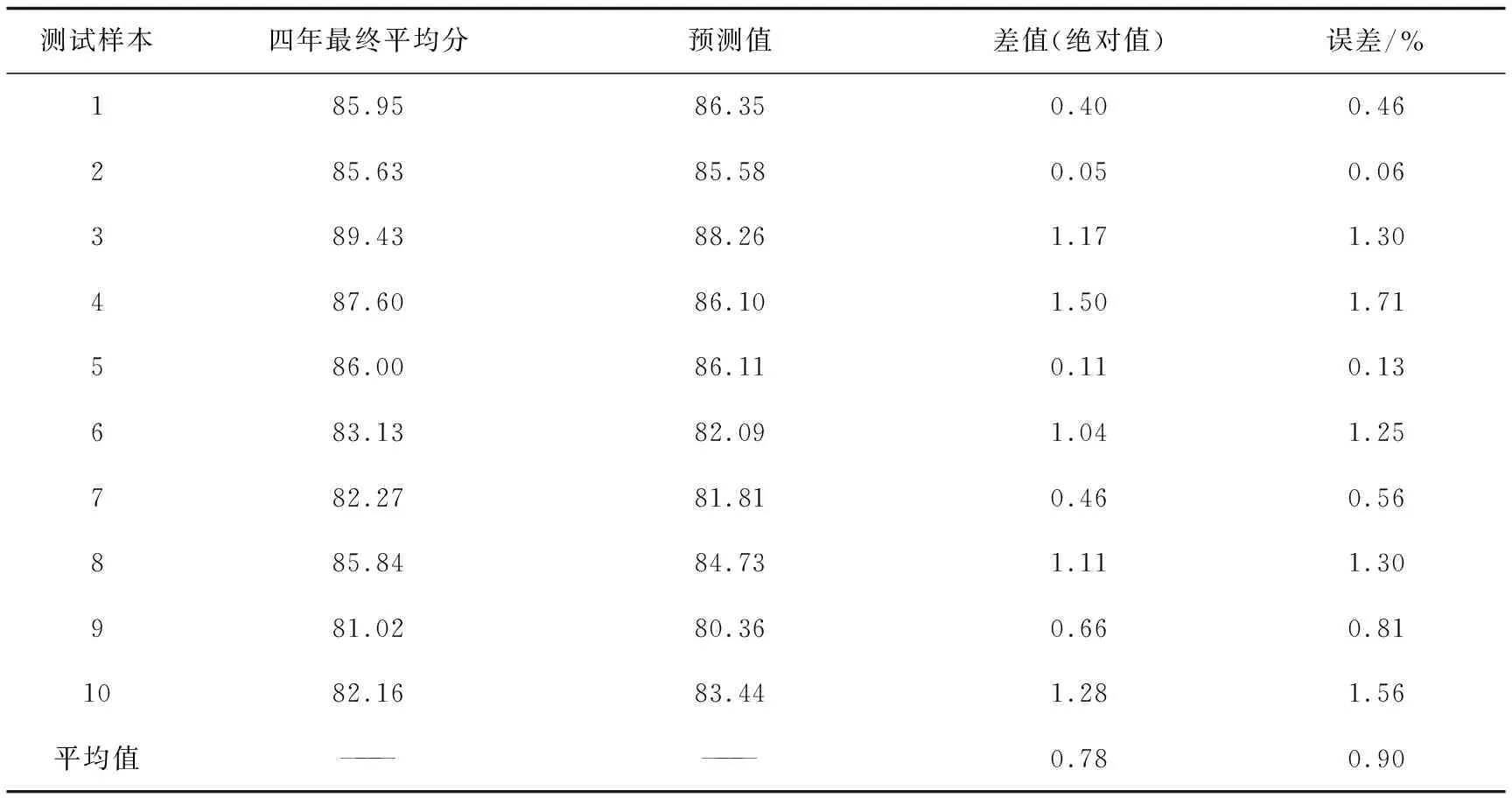
表6 实验3实际值与预测值对比
(3)实验2。
实验2的48个训练样本得到的标准线性回归方程为:
0.164X6+(-0.010)X7+(-0.013)X8+(-0.004)X9+0.017X10+0.001X11+
0.087X12+0.167X13+0.093X14+0.284X15+0.119X16+(-0.073)X17
(13)
通过模型预测出剩余5个测试样本的预测值,如表7所示。预测差值最高不超过1.4分,平均误差为0.97%,预测性能精度较高。
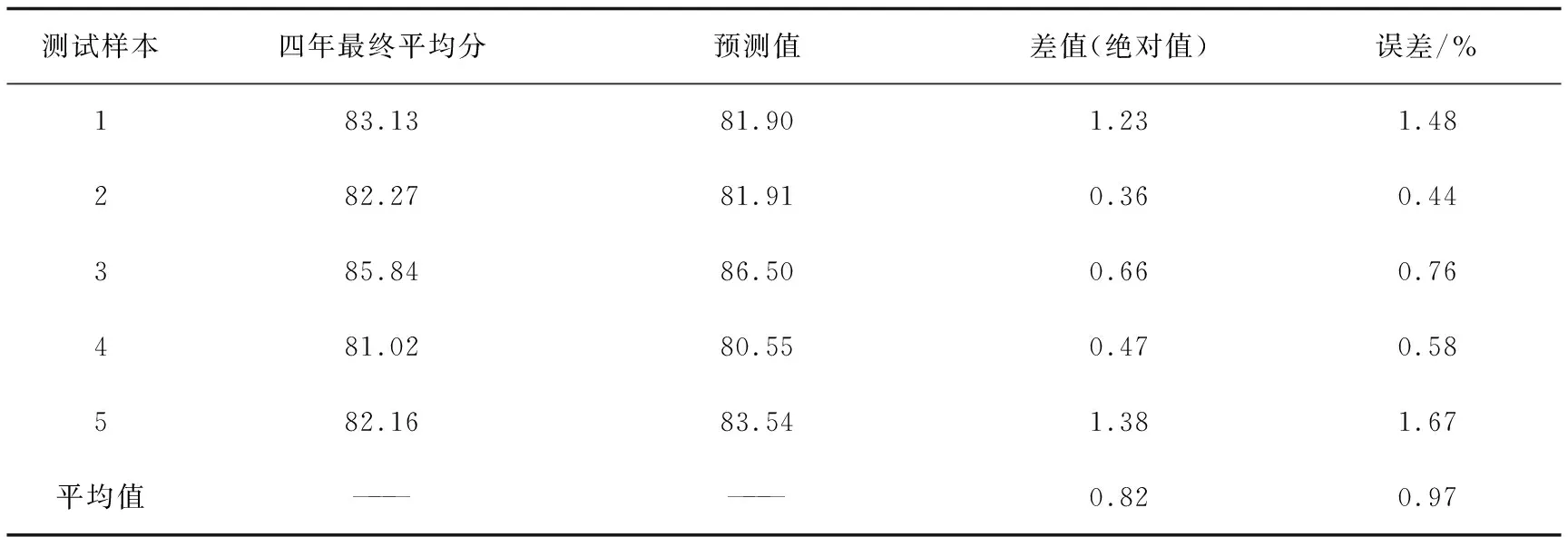
表7 实验2实际值与预测值对比
(4)实验1。
实验1的50个训练样本得到的标准线性回归方程为:
+(-0.010)X7+0.010X8+0.010X9+0.038X10+(-0.011)X11+0.088X12
+0.185X13+0.094X14+0.268X15+0.107X16+(-0.084)X17
(14)
通过模型预测出剩余3个测试样本的预测值,如表8所示。预测差值最高不超过1.2分,平均误差为0.61%,预测性能精度较高。
通过这四个实验的单次实验表明,结果与训练样本数量关系不大,可行性较强。并且构建的预测模型具有较高的精度,可以为学校改进教学方案,提高教学质量提供一定的参考信息,具有重要的意义。
3 结束语
成绩预测是提高教学质量的重要辅助工具之一,但是目前多是基于全部成绩进行研究。因此该文提出利用多元回归方法构建通过一年级成绩预测毕业成绩的预测模型,并以某学校计算机应用专业的学生课程成绩为研究对象开展研究。大量实验结果表明可以利用一年级成绩预测毕业成绩,并且该文构建的预测模型具有较高的准确度。该研究可以为教学的改进提供依据,为老师对学生采取帮扶措施提供参考。但学生成绩预测是一个比较复杂的课题,本次研究只考虑了成绩因素,因此在下一步的研究中会考虑学科背景、素质测评等更多因素,构建更加精确的预测模型。
