乘法器模块在FPGA中的实现
2012-11-08李彦孚
李彦孚,宋 路
(长春理工大学 电子信息工程学院,长春 130022)
乘法器模块在FPGA中的实现
李彦孚,宋 路
(长春理工大学 电子信息工程学院,长春 130022)
作为数字信号处理领域的基本运算单元,乘法器在其中起到了至关重要的作用。本文设计了三种基于FPGA的数字乘法器模块,包括传统乘法器,LUT乘法器和Booth算法的乘法器,利用Modelsim仿真软件分别对三种算法进行了仿真,并用QuartusII软件对所编写的Verilog程序进行编译综合,这里用到的FPGA芯片是Altera公司生产的cycloneII器件,最后对结果进行了说明。
数字信号处理;LUT乘法器;Booth乘法器;FPGA
0 引言
随着现代通信和数字信号处理对于数字系统的实时性要求越来越高,乘法器性能的优劣将起到至关重要的作用。在数字信号处理中包括各种各样的运算,例如卷积运算,数字滤波,FFT,相关计算,矩阵运算等,而这些运算中都有大量的类似于A(k)B(n-k)的运算,因此乘法和累加是数字信号处理中基本的大量的运算。DSP(digital signal processor)中虽然有内嵌的乘法器,但只对应于特定的算法,相较于DSP,很多类型的FPGA器件中虽然有内置的乘法器,但是可以利用Verilog语言进行软乘法器模块的编写,这就使乘法器的设计非常灵活。因此,考虑到FPGA的资源一般还算丰富的条件下,自己编写乘法器模块。
对于乘法器的设计,此前已有很多相关的算法产生,但主流的乘法器归纳起来主要有以下几类,包括传统乘法器,移位相加乘法器,LUT乘法器,Booth算法乘法器。本文对传统乘法器,LUT乘法器,Booth算法乘法器进行了软件设计,利用Modelsim仿真软件进行了仿真,在QuartusII开发平台上基于cycloneII器件对程序进行了综合验证,最后对几种算法的乘法器的时钟消耗以及器件逻辑资源的占用等情况进行了比较和分析。
1 基本原理及仿真
1.1 传统乘法器
可以说传统乘法器是各种各样乘法器研究的基础,因此对于传统乘法器的掌握是十分有必要的。
在传统的概念上乘法等价于“重复几次”。比如n*m,也就是对n进行m次的累加,每进行一次累加操作,乘数m就递减一次,直到乘数的值减为0,便得到乘积。基于这样的思想,我们进行乘法器模块的设计,但其中需要注意的一个问题是乘积结果的正负。其实乘法器中乘积结果的正负就是两个乘积项进行异或的结果。表1给出了这种映射关系。

表1 乘法器中乘积结果的正负关系
图1给出了一个8bit*8bit传统乘法器的仿真分析图。
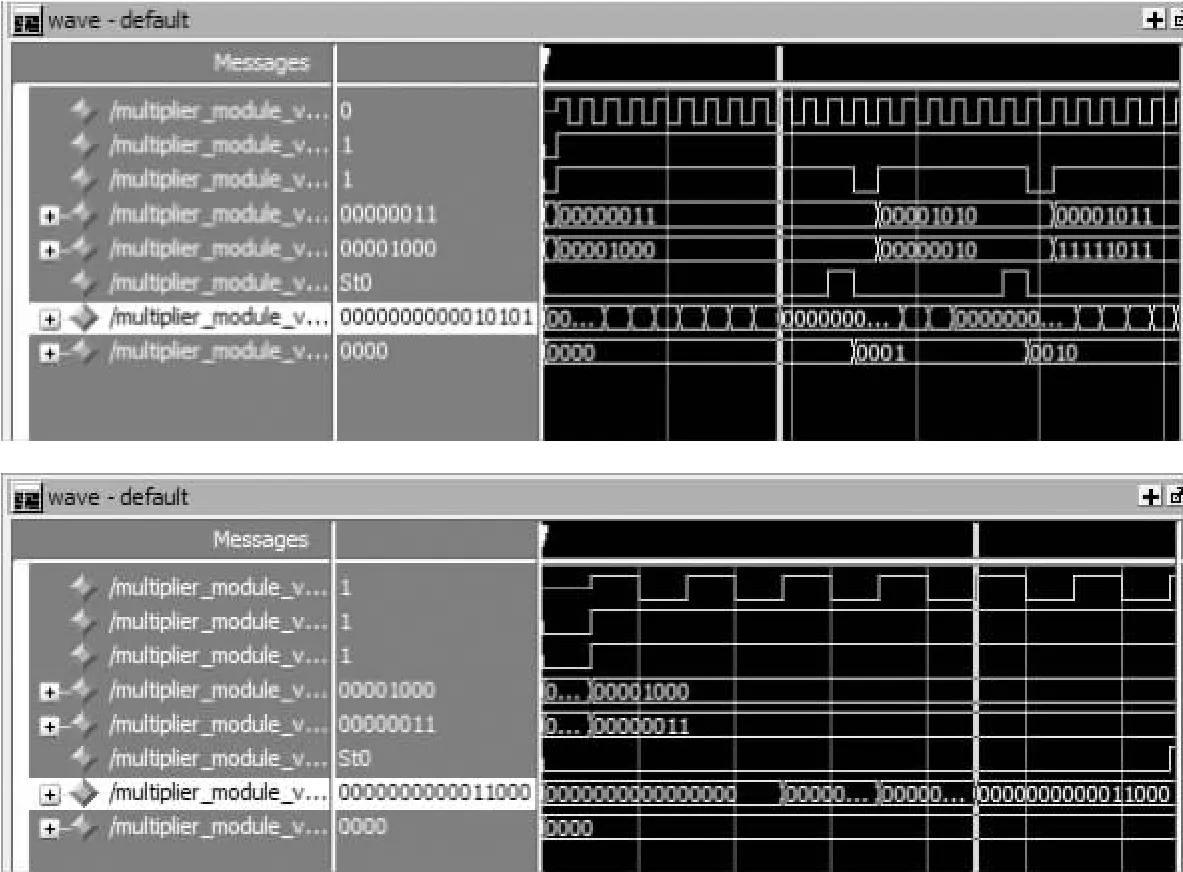
图1 传统乘法器的仿真分析图
由图1可以看出,传统乘法器的设计虽然简单,但是此种算法的时间受限于被乘数的大小,被乘数越大,消耗的时钟也就越多。
1.2 LUT 乘法器
所谓LUT乘法器就是查找表乘法器,顾名思义,这种方法就是事先把各种各样的结果储存在一个表中,然后我们以“查表”的方式取得乘积的结果。图2给出了该种乘法器的基本原理框图。相对于传统的乘法器,LUT乘法器要快很多,因为查找表乘法器只需少量的时钟,去查表就可以完成乘积结果的获取。而非查表的乘法器要消耗相对较多的时钟,才能求得乘积结果。但这种乘法器受限于乘积项存放的存储器的速度,比较适用于位数较少的乘积项,对于位数较多的乘积项,需要的寻址范围也自然会增大,因此不适用位数较高的乘法运算。
本文设计的是8Bit*8Bit的LUT乘法器,仿真结果如图2所示。
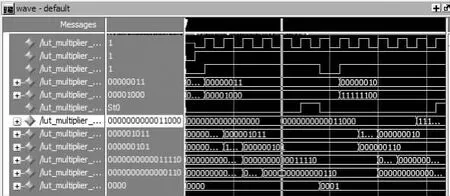
图2 LUT乘法器仿真结果
1.3 Booth算法乘法器
Booth算法是一种比较好的带符号数乘法,它实际上是一种“加码”乘法运算,采用相加和相减的操作计算补码数据的乘积,基本原理可以先从数学的角度进行理解。Booth算法对乘数从低位开始判断,根据两个数据位的情况决定进行加法、减法还是仅仅移位操作。判断的两个数据位为当前位及其右边的位(初始时需要增加一个辅助位0),移位操作是向右移动。
表2给出了这种算法的运算规则。该规则首先在乘数B的最低位加一个辅助位0,然后从辅助位开始两位两位读取,相邻两位的值决定了执行何种操作。当前2位判断过后,需将乘积寄存器右移一位,开始新的判断和操作。对于带符号数的运算,乘积寄存器进行右移操作时,必须对中间结果进行符号扩展,是将原来的符号位复制到移位后的最高位。
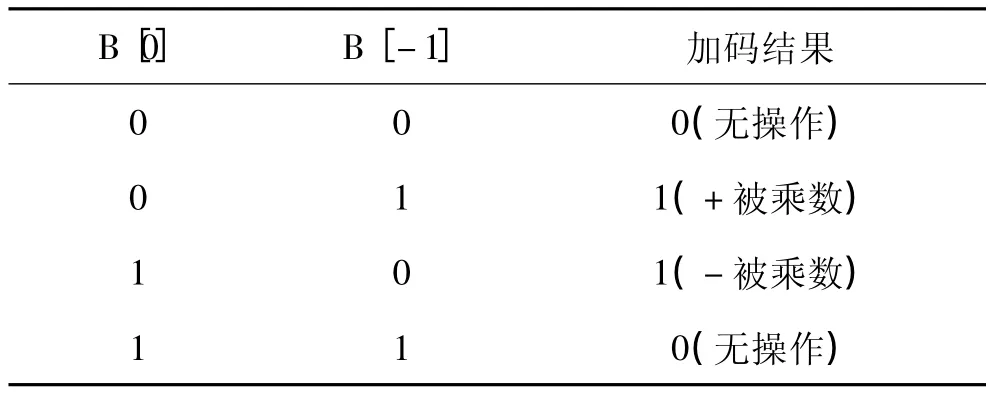
表2 Booth算法乘法器运算规则
图3给出了这种算法的具体操作流程。本文是以A(4Bit)*B(4Bit)的乘法器为例,先初始化一个P空间,P[4:1]填入乘数 B 的值,P[8:5]初始化为 0。首先判断 B[0]位和 B[-1]位,根据上表的运算规则,使P[8:5]与被乘数A进行相应的运算。判断P[8],如果是逻辑0,P空间需右移一位补0;如果是逻辑1,P空间右移一位补1。然后进入下一次的循环,接着对B[1]位和B[0]为进行判断,如此反复,直到执行完N次循环(这里的N取4),便得到乘积结果P[8:1]。
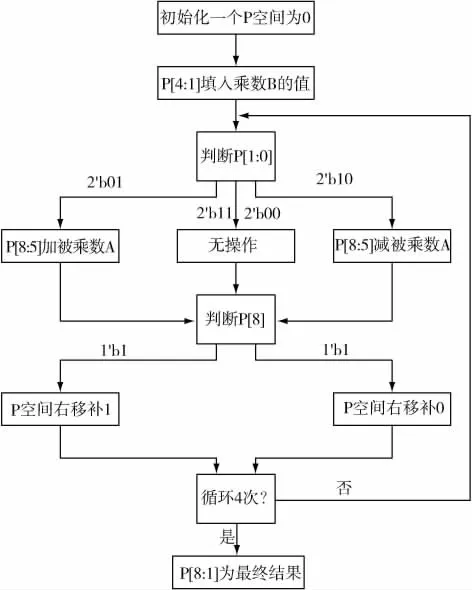
图3 算法的操作流程图
图4为8Bit*8Bit的Booth乘法器的仿真波形图。

图4 Booth乘法器的仿真波形图
2 编译综合
进行了功能仿真后,本文针对特定的FPGA芯片(cycloneII EP2C5Q208C8),利用QuartusII开发平台,进行了不同算法程序的在线下载。表3给出了8Bit*8Bit乘法器的三种不同算法的综合结果。

表3 乘法器的三种不同算法的综合结果
由综合的结果可以看出,对于8bit*8bit的乘法器而言,传统乘法器占用了较多的时钟周期,这主要与乘数的值有关,但从其硬件资源的使用情况来看,这种方法还是比较实用的。LUT乘法器的运算速度要高于传统乘法器和Booth乘法器,但是这是以牺牲硬件资源为前提的,所以这种方法比较适于位宽较小的乘法的运算。虽然此处的Booth算法的运算速度没有体现出其优势,但是经过验证,对于16位的乘法运算,Boot乘法器的运算速度要远远高于LUT乘法器,并且此种算法的硬件资源的耗用也是可以接受的。可见,Booth算法的综合优势明显,因此得到更广泛的应用。
3 结语
相较于模拟乘法器,数字乘法器的精度,可靠性和运算速度上都有很大的优势,对于通信中的调制解调等信号处理领域的发展都有很大帮助。本文分别对传统乘法器,LUT乘法器和Booth乘法器的基本原理进行了说明,并且编写了基于这些算法的Verilog程序,最后进行了仿真分析和综合验证。通过比对,我们发现几种乘法器在不同的应用场合下,它们的性能是有所区别的。因此,我们可以根据自身的需要来设计满足要求的乘法器。
[1] 吴戈.VerilogHDL与数字系统设计简明教程[M].北京:人民邮电出版社,2009.
[2] 夏宇闻.从算法设计到硬线逻辑的实现[M].北京:高等教育出版社,2000.
[3] 鞠芳,马昕,田岚.基于FPGA的数字乘法器性能比较[J].电子器件,2011,34(6):718-722.
[4] 应征,吴金,常昌远,等.高速乘法器的性能比较[J].电子器件,2003,26(1):42-45.
[5] 刘凌,胡永生.数字信号处理 FPGA实现[M].北京:清华大学出版社,2003.
The Realization of Multiplier Module in FPGA
LI Yan-fu,SONG Lu
(School of Electronics and Information Engineering,Changchun University of Science and Technology,Changchun 130022,China)
As the basic computing unit in digital signal processing area,multiplier plays a crucial role.This paper designs three digital multiplier modules based on FPGA,including traditional multiplier,LUT multiplier and Booth algorithm multiplier.With Modelsim simulation software,the three algorithms are simulated,and the written Verilog program is compiled with QuartusII software,here the FPGA chip used is the cycloneII device produced by Altera Company,finally the results are illustrated.
digital signal processing;LUT multiplier;Booth multiplier;FPGA
TP331.1+1
A
1009-3907(2012)08-0933-04
2012-04-26
李彦孚(1987-),男,吉林长春人,硕士研究生,主要从事数字视频与图像处理技术研究;宋路(1952-),女,吉林长春人,教授,博士生导师,主要从事光通信系统理论与无线通信技术研究。
责任编辑:吴旭云
