间歇通信的非线性多智能体系统协调跟踪控制
2022-04-02张瑀航姜玉莲崔立朝王海伟
张瑀航,姜玉莲,崔立朝,王海伟
(长春工业大学 电气与电子工程学院,吉林 长春 130012)
0 引 言
近年来,多智能体系统协调合作在航天器[1]、无人飞行器[2]、传感器网络[3]、移动机器人[4]以及无人地面车辆[5]等领域应用普遍,受到了广泛关注和深入研究。作为多智能体协调控制的基本问题之一,一致性控制问题已成为热门话题[6-7]。
在多智能体网络系统中,每个智能体都具有一定的感知、决策和通讯能力,其一致性问题是指多智能体网络的个体按照设计的控制规则,相互传递信息,相互影响,随着时间的推移,使得所有智能体的状态或输出趋于一致[8-9]。近年来,多智能体一致性问题的研究取得了许多成果[10-11]。文献[12]对随机多智能体系统的一致性控制方法进行了综述。Ni和Cheng[13]针对固定和切换通讯拓扑结构的多智能体系统,提出带有领导者的一致性协议。陈刚等[14]研究了受到未知干扰的多智能体系统的鲁棒一致性控制方法。
由于带宽、技术水平、通信成本等条件的限制,多智能体系统中的信息交互并不是每时每刻都在进行,因此,间歇通信的多智能体系统一致性问题越来越受到人们的关注。Wen等[15]研究了间歇通信下无领导者的高阶线性多智能体的一致性。文献[16]研究了间歇通信下异构线性多智能体系统的输出包含问题。文献[17]研究了在有向图下具有间歇通信的连续/离散广义线性多智能体系统的一致性问题。上述成果主要解决的是无领导者的间歇通信多智能体系统一致性问题。而具有领导者的多智能体分布式协调跟踪控制不仅能够节省控制能量和成本,还能使系统以更快的速率进行收敛。所以基于协调跟踪控制的领导-跟随一致性问题成为一个热门话题[18]。在实际应用中,由于很多系统本质上都是非线性的[19-20]。因此,该文研究了间歇通信的非线性多智能体系统分布式协调跟踪控制问题。
针对间歇通信的非线性多智能体系统,该文提出了一种新的分布式协调跟踪控制方法,以保证非线性智能体的状态能够跟踪领导者。同时,利用切换系统理论和LMI技术,得到了分布式协调跟踪算法实现非线性领导-跟随多智能体系统一致性跟踪的充分条件。并进一步证明了当通信速率大于某一阈值时可以保证所设计的分布式协调跟踪控制器实现间歇通信情况下的一致性跟踪目标。
1 预备知识和问题描述
1.1 预备知识
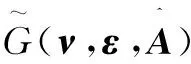
对于一个有向图,有下列性质。
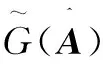
1.2 问题描述
该文研究的多智能体系统由N个跟随者和一个领导者组成,具有非线性动态的多智能体动力学方程为:
(1)
(2)
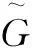
假设1:存在一个非负常数r使得下列式子成立:‖f(y,t)-f(z,t)‖≤r‖y-z‖,∀y,z∈Rn,t≥0,则说明此式满足Lipschitz条件。
在一些实际应用中,由于通信通道的不可靠性、物理设备的故障等,使得智能体之间的交流可能只在某些断开的时间间隔中进行。该文考虑间歇通信情况,为实现跟随者能够协调跟踪领导者的控制目标,提出一种间歇通信的分布式协调跟踪控制器:
(3)
其中,Tp=[kρ,kρ+ρ),Tq=[kρ+δ,(k+1)ρ),c>0为耦合增益,K∈Rm×n是反馈控制增益矩阵,并且k∈Z,标量ρ>δ>0。

将新的分布式协调跟踪控制器(3)作用于多智能体系统(1),得到间歇通信的闭环多智能体系统:
(4)
其中,i=1,2,…,N。
定义领导者与跟随者的一致性跟踪误差为:ei=xi-x0,则由式(2)和式(4)可得:
(5)
其中,H=L+G。
2 协调跟踪控制器设计及稳定性分析
本节,将给出分布式协调跟踪控制器(3)的设计过程,实现系统(1)在强连通通信拓扑结构下的一致性跟踪目标。
首先,给出分布式协调跟踪控制器(3)的设计算法,即算法1:
(1)求解下列矩阵不等式(LMI)。
(6)

(2)求解下列LMI。
(7)
得到矩阵Q-1>0,常数τ>0。
(3)选择耦合增益c>α/a(H),其中a(H)由引理1得到。
定义rk=δk/ρ为第k个时间间隔的通讯速率,进而给出主要结论。
证明:构建Lyapunov函数
其中,Ξ=diag{ξ1,ξ2,…,ξN},使得ξTL=0和ξTIN=1的正向量ξ=(ξ1,ξ2,…,ξN)T,正定矩阵S和Q为LMIs (6)和(7)的对称正定解。
当t∈Tp时,
eT(t)(Ξ⊗S-1A+Ξ⊗ATS-1)e(t)+
2eT(t)(ΞcH⊗S-1BK)e(t)+
(8)
eT(t)(ΞcH⊗S-1BBTS-1)e(t)+
(9)
根据假设1和Young不等式得:
r‖eT(t)(Ξ⊗S-1)‖•‖e(t)‖≤
IN‖•‖e(t)‖≤
(10)
进而由式(10)可得:
(11)
结合引理2和算法1,整理(11)得:
(12)
由(6)及Schur补理论可得:
-βeT(t)[Ξ⊗S-1]e(t)
(13)
当t∈Tq时,
eT(t)(Ξ⊗QA+Ξ⊗ATQ)e(t)+
(14)
根据假设1和Young不等式得:
eT(t)(Ξ⊗QA+Ξ⊗ATQ)e(t)+
(15)
reT(t)[Ξ⊗Q]e(t)
(16)
当分布式协调跟踪控制器(3)在切换时刻t=kρ和t=kρ+δ时,在(13)和(16)的基础上可得:
V(ρ)<θe(ρ-δ0)V(δ)<θ2e-βδ0+τ(ρ-δ0)V(0)=
e-γ0V(0)
(17)
其中,γ0=βδ0-τ(ρ-δ0)-2lnθ。
(18)
其中,γi=βδi-τ(ρ-δi)-2lnθ>0,i=0,1,…,k,对于任意t>0,存在zρ (19) 因此定理1能够使多智能体系统(1)实现一致性跟踪目标。证毕。 定理1和算法1主要解决了多智能体系统(1)具有非线性动态情况下的一致性跟踪问题,当非线性动态f(xi(t))=0和f(x0(t))=0时,间歇通信的分布式协调跟踪控制协议为: (20) 其中,F=Rm×n为反馈控制增益矩阵。 分布式跟踪控制协议(20)的设计算法,即算法2如下: (1)求解下列LMI: AS'+S'AT-α'BBT+β'S'<0 (21) (2)求解下列LMI: AQ'-1+Q'-1AT-2τ'Q'-1<0 (22) 得到矩阵Q'-1>0,其中常数τ'>0为正常数。 (3)选择耦合增益c'>α'/a(H),其中a(H)由引理1得到。 下面给出解决非线性动态为零即线性多智能体系统一致性跟踪问题的推论。 证明:此证明过程与定理1证明过程类似,在此不再赘述。 本节以非线性多单摆网络系统作为研究对象,通过仿真实验和对比分析,验证基于间歇通信的分布式协调跟踪控制方法的有效性。 考虑由5个直流电机驱动的单摆系统(如图1所示)和一个领导者所构成的多单摆网络系统,其通信拓扑结构如图2所示。其中节点0代表领导者,其余则为跟随者。多单摆网络系统中跟随者的运动模型如式(1)所示,i=1,…,N,N=5,A,B和f(xi)如下所示: 其中,u表示端子电压,R和L分别表示电枢电路的电阻和电感,ia表示电枢电流,E表示直流电机的反电动势,摆球的质量用m表示,l是摆杆的长度。KT和KE分别表示电机转矩常数和反电动势常数。 领导者的动态方程如式(2)所示,设定多单摆网络系统的参数为: 其中,f(xi(t))和f(x0(t))满足假设1中的Lipschitz条件。 假设通信持续时间δ=3.5,则每一个时间间隔为[5k,5k+3.5),k∈Ζ。控制参数τ=0.1,β=0.2。根据算法1及控制协议(3),得到反馈增益矩阵K=[-15.25,-16.62,-2.82],选择c=40。在仿真中,考虑两个时间间隔,即t=[5k,5k+3.5)和t=[5k+3.5,5k+5)。通信模式如图3所示。 若Y=1说明系统中相邻智能体之间正在进行通信,Y=0则说明系统中相邻智能体之间通信中断。 图4~图6为间歇通信设计的控制协议作用下的一致性跟踪仿真结果,仿真结果验证了该文所设计的分布式协调跟踪控制器(3)能够使间歇通信的非线性多单摆网络系统(1)~(2)的角位移、角速度和电枢电流达到一致性跟踪目标。 该文研究了间歇通信的非线性领导-跟随的多智能体系统的分布式协调跟踪问题,提出了一种新的基于间歇通信的一致性跟踪控制协议,并给出了设计过程。同时,利用切换拓扑理论和LMI技术分析了多智能体系统的稳定性,以保证多智能体的状态协调跟踪领导者。由于现实生活中系统受到干扰及延时等综合因素的影响,所以在之后的研究,会更加切合实际,考虑间歇通信的多智能体系统中存在时滞、干扰等情况,解决其分布式协调跟踪控制问题。
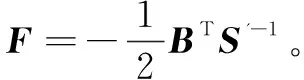
3 仿真实验
3.1 非线性多单摆网络系统

3.2 结果有效性实验
4 结束语
