一种通用的卫星地面防护范围计算方法

李 蕊，邓亭强，窦修全，徐海生

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.河北省电磁频谱认知与管控重点实验室，河北 石家庄 050081)

0 引言

卫星不受地区及恶劣天气影响，能够长时间大范围的监视和跟踪电磁信号，及时获取电子系统特征、地理属性和电磁活动等，因此卫星作为一种新型的通信载体受到世界各国的关注[1-4]。在通信对抗中，经常需要知道卫星的地面防护范围，所谓地面防护范围是指通过干扰卫星上行链路导致卫星下行通信失效的区域，显然研究卫星地面防护范围在布设干扰站以及抗干扰等方面等具有非常重要的军事应用价值[5-9]。目前，尚未有文献研究卫星地面防护范围的计算方法，但有少量学者针对地球同步轨道卫星给出了波束覆盖区域的相关计算。文献[1]研究了全球波束覆盖区域的计算，文献[10]中研究了在给定地球同步卫星经纬度、卫星天线波束中心点与地球的交点以及波瓣宽度时卫星波束覆盖区域的计算方法，然而存在某些极端情况即卫星波束中心与地球没有交点，此时文献[10]中的方法将会失效。文献[11]针对地球同步卫星提出了一种点波束倾斜照射时覆盖范围的计算方法，但此算法是在星地相对静止的前提下提出的，当卫星为低轨卫星时此算法将不再适用。

本文提出了一种通用的卫星地面防护范围计算方法，首先判断干扰站是否在卫星上行波束覆盖范围内，如果不在，则地面防护范围为零；否则，需要计算卫星下行波束覆盖区域。本文所提出的方法适用于任意高度的卫星，且对于干扰站位置、卫星上下行波束宽度以及指向均不限，计算方法简单易行，实用性强。接下来将依次介绍卫星地面防护范围的数学模型、计算流程和算法复杂度分析以及相应的仿真对比。

1 卫星地面防护范围数学模型

不失一般性，Oe表示地心，Re为地球半径，卫星S的大地坐标为(LS,BS,HS)，G点表示星下点其大地坐标为(LG,BG,HG)，显然LG=LS，BG=BS，HG=0。卫星地面防护范围示意图如图1所示。

图1 卫星地面防护范围示意图Fig.1 Schematic diagram of satellite ground protection range

图中，射线SMul、SNul、SEul为卫星上行波束边缘线及中心线，γul为上行半波束宽度，干扰站T的大地坐标为(LT,BT,HT)；射线SMdl、SNdl、SEdl为卫星下行波束边缘线及中心线，γdl为下行半波束宽度。干扰站通过干扰卫星上行链路，导致下行通信失效的区域即为地面防护范围。

以卫星S为原点的站心坐标系(又称之为东北下坐标系，简称NED坐标系)，如图2 所示，φ为卫星波束中心SE在NED坐标系下定义的俯仰角，θ为波束中心在NED坐标系下定义的方位角。需要说明的是，某些情况下会给定其他坐标系下的波束指向角，例如给定平台坐标系下波束的俯仰角和方位角，均可通过坐标转换公式转到NED坐标系中。

图2 波束中心线示意图Fig.2 Beam centerline diagram

2 计算流程及算法复杂度分析

卫星地面防护范围的计算流程主要分为以下3个步骤，如图3所示：

① 判断干扰站是否在卫星上行波束覆盖范围内：根据卫星位置、上行波束俯仰角φul和方位角θul，确定卫星上行波束中心线；利用卫星位置和干扰站位置，计算上行波束中心线与卫星和干扰站连线的夹角；将计算出的夹角与上行波束宽度进行对比，判断干扰站是否在卫星上行波束覆盖范围内；

② 如果干扰站在卫星上行波束覆盖范围内，则执行步骤③；否则，输出卫星的地面防护范围为0；

③ 计算卫星下行波束覆盖区域，此区域即为卫星地面防护范围：根据卫星位置、下行波束俯仰角φdl和方位角θdl，确定卫星下行波束中心线；利用卫星下行波束宽度，计算下行波束边缘线，并进一步求出各边缘线与地球的交点，从而得到卫星下行波束覆盖区域。

图3 卫星地面防护范围计算流程Fig.3 Calculation process of satellite ground protection range

2.1 判定干扰站是否在卫星上行波束覆盖范围内

(2) 确定卫星与干扰站的几何方向

若待转换点的大地坐标为{L,B,H}，转换成地固坐标为{xe,ye,ze}[12-13]，则有

(1)

式中，e2=0.006 694 379 990 13是第一偏心率平方，Ne是当地卯酉圈曲率半径。

若NED坐标系下站心的大地坐标和地固坐标分别为{Lo,Bo,Ho}、{xo,yo,zo}，待转换点的地固坐标为{xe,ye,ze}，转换成NED坐标系为{xn,yn,zn}[14]，则有

(2)

(3) 判定干扰站T是否在卫星上行波束覆盖范围内

将计算出的β与上行半波束宽度γul进行对比，如果β≤γul，且目标位于波束照射地球的正面而非背面，则判定干扰站在卫星可视范围内；否则干扰站不在卫星可视范围内，此时卫星地面防护范围为零。

2.2 卫星下行波束覆盖区域计算

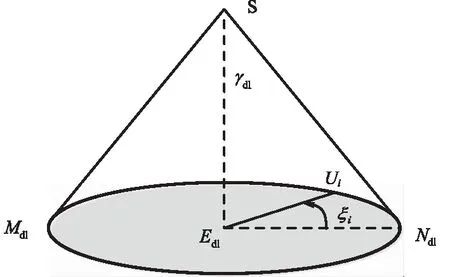
图4 波束覆盖简图Fig.4 Beam coverage diagram

(3) 下行波束覆盖边缘点

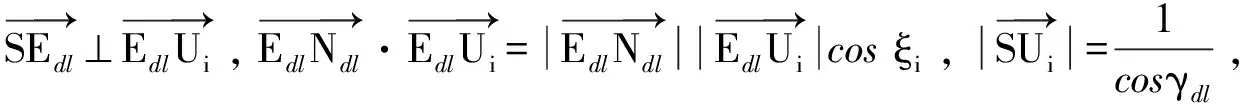
i=1,2,…,L。

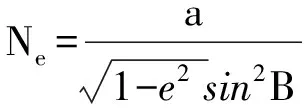
2.3 算法复杂度分析

本文所提出的卫星地面防护范围计算方法包括两部分：第一部分为判定干扰站是否在卫星上行波束覆盖范围内，需要进行3次坐标转换(每次坐标转换需要9次乘法和6次加法)，3次求模运算(每次求模运算需要3次乘法、2次加法和1次开方)，1次求角度运算(需要2次乘法、1次除法、1次求反余弦和2次加法)；第二部分为卫星下行波束覆盖区域计算，针对每一个边缘点需要求解2个一元二次方程(求解1次一元二次方程需要20次乘法、3次除法、1次开方和12次加法)，若设置覆盖区域边缘点个数为L，则需要求解2L次一元二次方程。经分析可以得出，第一部分的运算量基本可以忽略，整个算法的计算复杂度约为48×L，是O(L)量级，随设定的数据规模L线性增长，满足实时要求。

3 卫星地面防护范围仿真及误差分析

3.1 仿真结果

本节对不同位置干扰站、不同高度卫星(地球静止卫星/低轨卫星/中高轨卫星)、不同波束宽度及指向的场景下卫星地面防护范围进行了仿真，并与STK软件的仿真结果进行对比以证明算法的有效性。进一步对极端情况卫星下行波束中心线与地球没有交点的场景进行计算仿真，以说明所提出算法更具通用性。

地球静止卫星位于东经100°、纬度0°、高度36 000 km，干扰站位于东经130°、北纬30°；上行波束俯仰角为87°、方位角为20°、半波束宽度为5°，下行波束俯仰角为85°、方位角为30°、半波束宽度为5°。经计算上行波束中心线与卫星和干扰站连线的夹角，且目标位于波束照射地球的正面，故判定干扰站在卫星上行波束范围内；进一步计算出卫星地面防护范围如图5所示。为证明算法的有效性，利用STK软件[15-17]得到卫星下行波束覆盖范围如图6所示。

图5 静止卫星地面防护范围仿真结果Fig.5 Simulation result of ground protection range of stationary satellites

图6 STK仿真结果Fig.6 Simulation results by STK

低轨卫星位于西经0°、纬度0°、高度800 km，干扰站位于西经10°、北纬10°；上行波束俯仰角80°、方位角150°、半波束宽度为50°，下行波束俯仰角83°、方位角60°、半波束宽度60°。经计算上行波束中心线与卫星和干扰站连线的夹角β=47.7°<50°，判定干扰站在卫星上行波束范围内；进一步计算出卫星地面防护范围如图7所示。为证明算法的有效性利用STK软件[7-8]得到卫星下行波束覆盖范围如图8 所示。

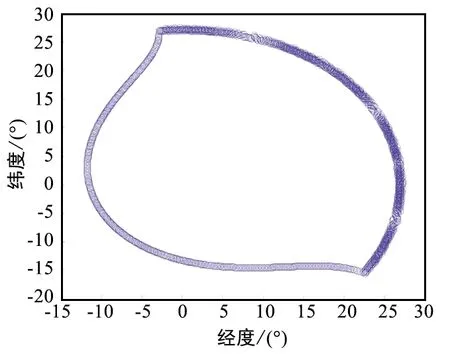
图7 低轨卫星地面防护范围仿真结果Fig.7 Simulation result of ground protection range of low-orbit satellites

图8 STK仿真结果Fig.8 Simulation results by STK

中高轨卫星位于东经122°、纬度0°、高度15 000 km，干扰站位于东经100°、北纬50°；上行波束俯仰角87°、方位角100°、半波束宽度为30°，下行波束俯仰角85°、方位角120°、半波束宽度10°。经计算上行波束中心线与卫星和干扰站连线的夹角β=12.8°<30°，判定干扰站在卫星上行波束范围内；进一步计算出卫星地面防护范围如图9所示。为证明算法的有效性利用STK软件得到可卫星下行波束覆盖范围如图10 所示。

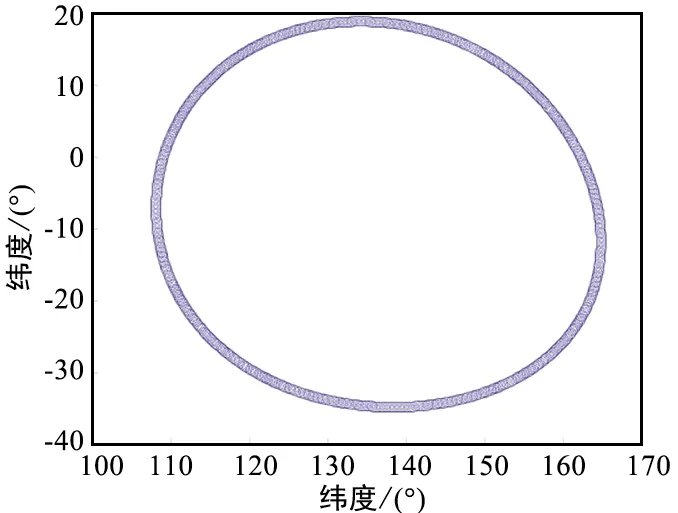
图9 中高轨卫星地面防护范围仿真结果Fig.9 Simulation result of medium and high orbit satellites

图10 STK仿真结果Fig.10 Simulation results by STK

假设确定干扰站在卫星上行波束区域内，在求解地面防护范围也就是卫星下行波束覆盖范围时，会面临卫星下行波束中心线与地球没有交点的极端情况，此时文献[10]的算法将失效，但本文中所提算法依然可以求解。卫星位于东经60°、纬度0°、高度10 000 km，下行波束俯仰角65°、方位角70°、半波束宽度5°，图12为STK软件仿真图，从图中看出卫星波束中心线与地球不存在交点，此时本文中的算法依然可以准确地给出地面防护范围如图11所示。

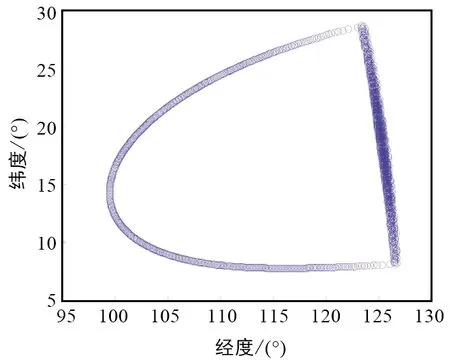
图11 极端情况下卫星地面防护范围仿真结果Fig.11 Simulation result in the extreme case

图12 STK仿真结果Fig.12 Simulation results by STK

3.2 误差分析

将STK仿真结果与本算法仿真结果进行对比，给出了部分边界点的对比结果如表1所示，经统计误差在12 km左右。误差产生的原因主要有几类：① 坐标转换过程中的误差：NED坐标与地固坐标互相转换时，由于地球并非正球，zn轴与地心存在偏角；地固坐标系转换成大地坐标系要经过迭代，也存在误差；同时随着算法的运行，这些误差会不断累积；② 算法流程中的计算卫星下行波束边缘点时，需要设置边缘点的个数L，L越大，需要的计算量越大，精细度更高，因而需要依据具体场景选择合适的L值。

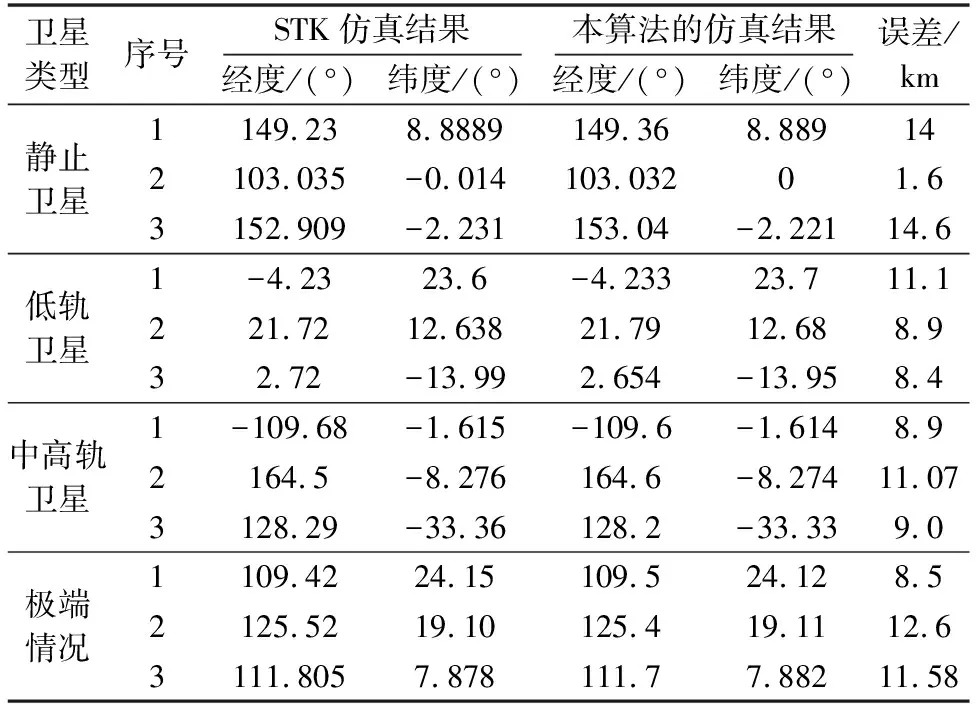
表1 仿真结果对比

4 结论

研究卫星对地防护范围具有十分重要的应用价值，是实施电子对抗与防护的第一步[18-19]。本文介绍了一种简单通用的卫星对地防护范围计算方法，该方法适用于任意高度的卫星，且对于干扰站位置、卫星上下行波束宽度以及指向均不限；同时结合具体场景，将本文所提出算法的仿真结果与STK的仿真结果进行对比，误差在12 km左右，证明了算法的有效性。