基于多时差的干扰源定位虚假点消除方法

柏如龙，霍立寰*，陈 兵，王海清，江 漫，杨 光，许瑞杰，廖桂生

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.河北省电磁频谱认知与管控重点实验室，河北 石家庄 050081；3.西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

0 引言

无源干扰源定位技术能够被动接收电磁波信号对干扰源进行测向定位，是现代电子对抗的重要手段[1-3]。以美国海军“NOSS”系列的海洋监视卫星为典型代表的基于卫星平台的时差定位体制，具有覆盖范围广、作用距离远、接收隐蔽、生存能力强的优点，能够迅速、准确地发现干扰源目标[4-6]，在各领域都有着重要作用和广泛的应用前景。

目前的卫星时频差定位主要包括时频差联合定位和多时差定位[7-12]，利用了不同卫星接收信号间的到达时间差(TDOA)和到达频率差(FDOA)。相比于时差测量，频差测量需要更多的参考站进行标校。因此，仅仅基于时差的三星时差定位体制成本更低、定位结果更为可靠。三星时差定位基于两条时差线进行交会定位，受卫星位置和干扰源位置的影响，两条时差线在某些时刻存在两个交点，难以确认干扰源的真实位置。文献[13-18]的研究主要集中在时差测量优化、定位方程解算等方面，包括不同体制信号的时差测量和校正方法，以及在不同定位场景下的定位方法。对于定位过程中出现的虚假点目标，仅基于目标位置的先验知识进行区分，当先验知识缺失时则无法判断虚假点。因此，亟需提出有效、稳健的虚假点消除方法。

针对上述问题，本文提出了基于多时刻测量的三星时差定位虚假点消除方法。首先建立了基于卫星多时刻测量时差结果的三星时差定位模型，然后基于WGS-84地球椭球模型建立多时刻定位方程组，最后推导了牛顿迭代的求解方法。通过多时刻的测量数据直接获取干扰源真实位置附近的定位结果，以该定位结果为初始值进行逐时刻精确定位。该方法能够在去除虚假点的基础上，得到更高精度的定位结果；同时在先验初始值偏差和时差测量误差较大的情况下仍具有良好的稳健性。

1 多时刻时差定位模型

图1为建立大地坐标系模型，包括地球椭球、指向0°经度方向的X轴，指向北极方向的Z轴，以及根据右手定则得到的Y轴。主星接收到干扰源信号，两颗辅星能够收到干扰源的旁瓣信号。每个时刻能够测量得到主星和辅星一、主星和辅星二的两个到达时间差，形成如图所示的时差面，在假设目标零高程的条件下，两个时差面和地球椭球面的交点即为三星定位的结果。由图1可以发现，两个时差面相交于一条直线，该直线与地球椭球面相交于两个点，一个为干扰源目标真实位置，另一个为虚假位置。在没有先验信息的情况下，仅依靠单时刻的时差难以区分真实位置和虚假位置。

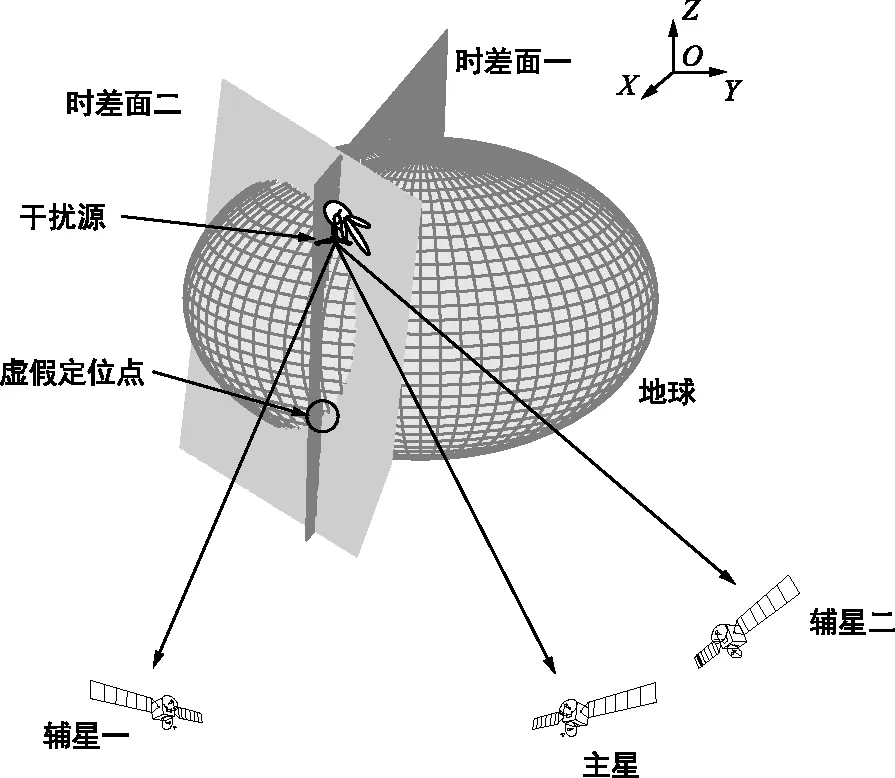
图1 三星干扰源定位示意Fig.1 Configuration of the tri-satellite interference source location

图2给出了时差线存在虚假点时的时差线相交情况，可以发现，多个时刻的时差线在真实位置处逐渐收敛于一点，而虚假点位置的时差线相交较为发散。因此，可以利用多个时刻的时差测量结果进行定位，从而判断出干扰源的真实位置。

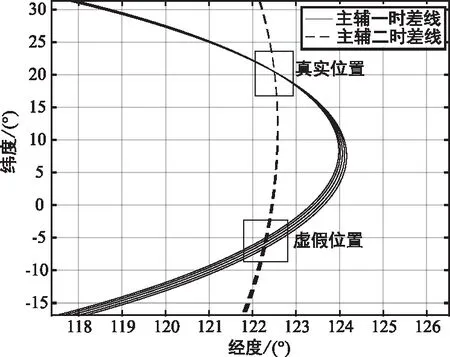
图2 三星时差线相交情况示意Fig.2 Intersection of tri-satellite time difference line

假设干扰源的坐标为(x,y,z)，第p个时刻时主星坐标为(xp0,yp0,zp0)，辅星一坐标为(xp1,yp1,zp1)，辅星二坐标为(xp2,yp2,zp2)，干扰源与辅星一和辅星二在第p个时刻的时差测量值分别为τp1和τp2，满足：

(1)

式中，c为光速，rp0，rp1和rp2分别为干扰源与主星、辅星一和辅星二在第p个时刻的距离。

根据距离的计算方式，以及地球椭球面模型，构造如下定位方程组。

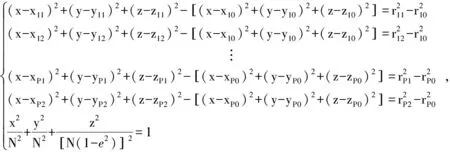
(2)

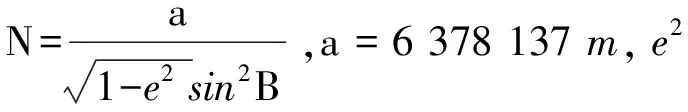
2 迭代求解算法

针对多时刻的测量结果构成的定位方程组，直接求解较为困难，考虑采用牛顿迭代方法求解。将以上方程组进行如下表示：

(3)

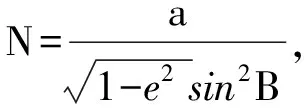
F(x,y,z)=0。

(4)

相应的Hesse矩阵为：

(5)

若第k次迭代中干扰源坐标为Pk=(xk,yk,zk)，则根据下式进行迭代。

Pk+1=Pk-[F′(xk,yk,zk)]-1F(xk,yk,zk)。

(6)

基于多时刻的三星定位方法步骤如下：

步骤1：根据P个时刻的时差τp1和τp2，计算对应的主辅星与干扰源的距离差(rp1-rp0)和(rp2-rp0)；

步骤2：初始化，设迭代次数k=0，干扰源目标初始位置P0；

步骤3：计算该次迭代过程中的Hesse矩阵F′(xk,yk,zk)，并根据式(6)得到下一次迭代中干扰源位置的估计结果Pk+1；

步骤5：判断目标运动属性，若为运动目标，则输出的定位结果作为初始值，对每个时刻的测量结果利用球形迭代方法得到定位结果的精确值。

算法流程如图3所示。

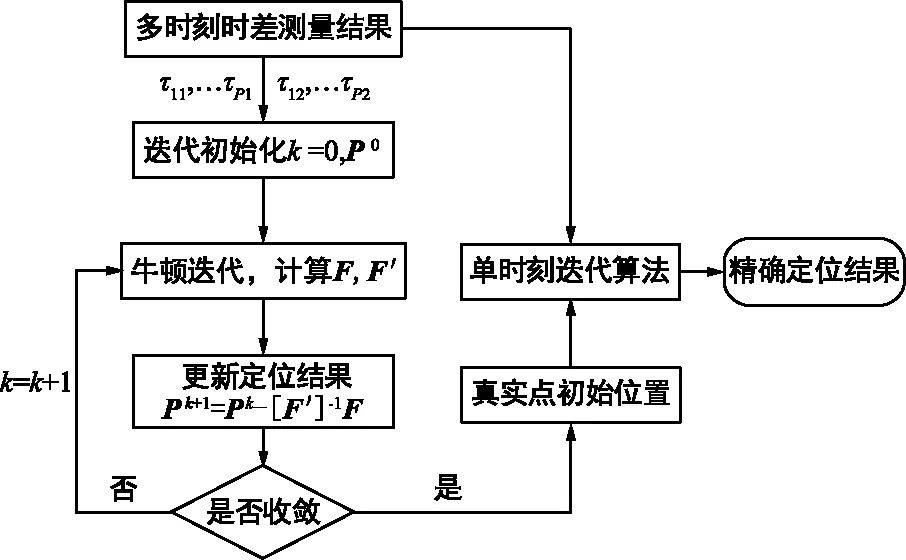
图3 基于多时刻测量的三星定位方法Fig.3 Tri-satellite localization method based on multi-time TDOA

3 仿真实验

在下面的仿真试验中，单时刻定位中定位时刻个数P=1，多时刻定位中定位时刻个数P>1，所提方法为利用多时刻定位去除虚假点后，将得到的定位结果作为单时刻定位的初始迭代值的方法。

3.1 多时刻定位影响因素分析实验

多时刻定位的性能主要与选取时刻个数、时间总长度有关，通过仿真实验探究其变化关系,如图4所示。

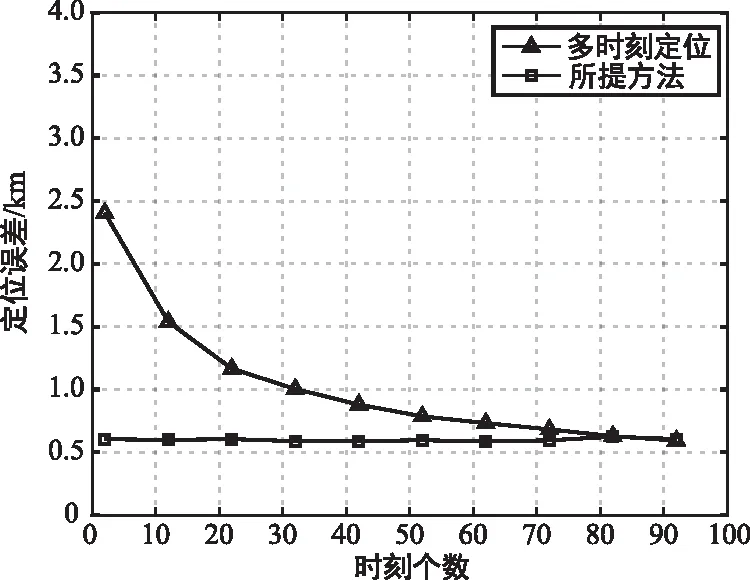
(a) 定位误差随时刻个数变化情况

(b) 定位误差随时长变化图4 多时刻定位方法性能影响试验Fig.4 Performance experiment of the multi-time location method

干扰源位置为125°E，30°N，时差测量误差为0.5 μs。首先仿真了时间总时长为20 min，多时刻定位和所提方法的定位误差随采用时刻个数的变化关系，可以发现：多时刻定位性能随时刻个数增加而提高，并不断趋近于所提方法，所提方法的定位误差基本不变。然后仿真了采用时刻个数为10，多时刻定位和所提方法的定位误差随总时长的变化关系，可以发现：多时刻定位性能随总时长增加而提高，并不断趋近于所提方法，所提方法的定位误差同样保持稳定，能够实现高精度地快速定位。

3.2 迭代初始值影响实验

通过仿真实验，对比迭代初始值对算法的性能影响。干扰源目标位置为125°E，30°N，时差测量误差在±0.5 μs内均匀分布，蒙特卡洛次数为500，采用3个连续时刻测量得到的时差值进行去除虚假点的目标定位，时间间隔为5 min，迭代初始值误差为初次迭代的先验经纬度偏差的均方根误差。图5给出了迭代初始值误差在0°～20°情况下，单时刻定位、多时刻定位和所提方法定位误差随迭代初始值误差的变化关系。可以发现：当迭代初始值逐渐增大时，单时刻定位的定位误差恶化明显，多时刻的定位方法基本不受迭代初始值的影响，但是在迭代初始误差很较小时，定位效果相比单时刻定位较差。而所提方法在多时刻定位的基础上，能够获得同时优于单时刻和多时刻的定位精度。

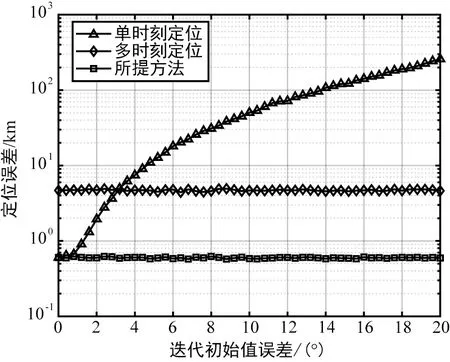
图5 不同方法的定位误差随迭代初始值误差的变化关系Fig.5 Location error of different methods versus the initial value error of the iteration

3.3 测量误差影响实验

对比3种方法随时差测量误差的变化关系如图6所示。干扰源目标位置为125°E，30°N，多时刻定位采用5个连续时刻测量得到的时差值以去除虚假点，时间间隔为4 min，迭代初始值偏差的均方根为1°，蒙特卡洛次数为500。可以发现，随着时差测量误差增加，3种方法的定位误差增大。其中，单时刻定位在时差测量误差较小时，主要受迭代初始值影响，受时差测量误差影响不明显。多时刻定位方法由于采用解方程组的方式，受时差测量误差影响较大。而基于多时刻测量的单时刻定位方法，在时差测量误差增大时具有良好的稳健性。

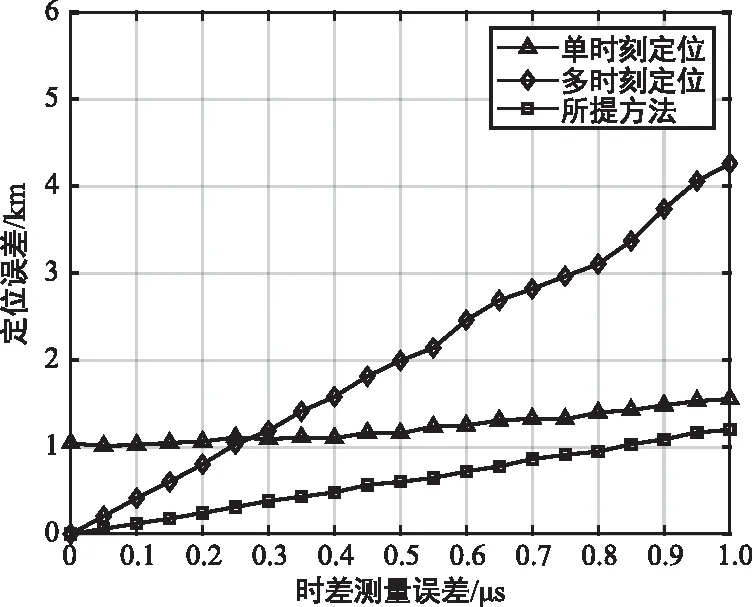
图6 不同方法的定位误差随时差测量误差的变化关系Fig.6 Location error of different methods versus the TDOA measurement error

4 实测数据验证

图7为某次实测数据的处理情况。

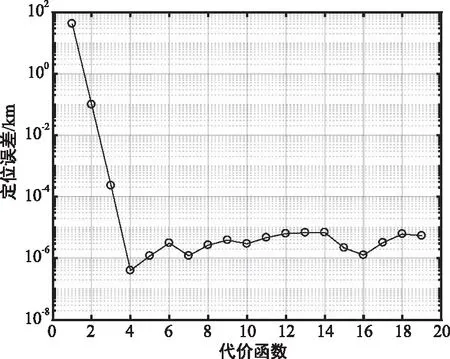
(a) 代价函数变化情况

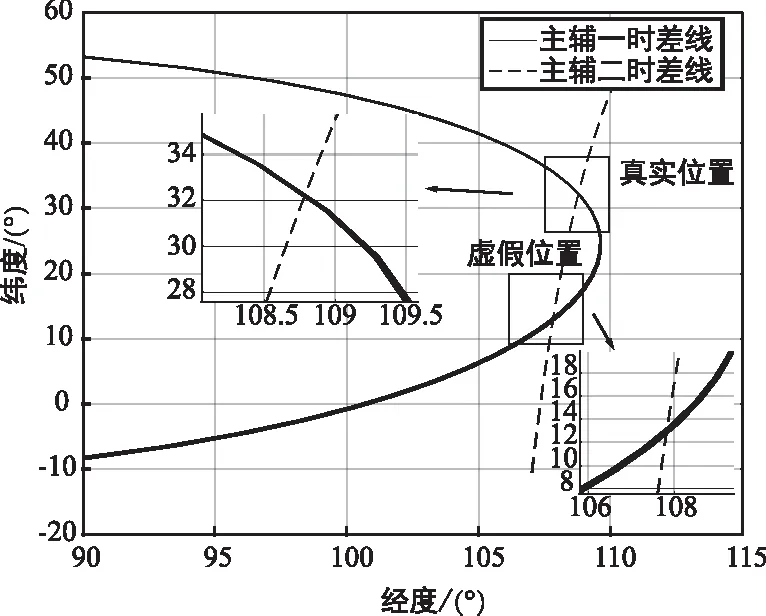
(b) 时差线相交情况图7 某次实测数据处理结果Fig.7 Results of the real data processing

实测数据处理后，多时刻定位方法能够定位误差为23.11 km，基于多时刻测量的方法得到定位误差为9.33 km。从迭代过程中代价函数δ的变化情况可以看出，进行迭代2～3次即可得到满足要求的结果。从时差线相交情况可以看出，由于时差测量存在误差，真实点位置多时刻的时差线也未能完全相交于一点。相比于真实点位置，虚假点处的时差线更为发散，因此能够采用基于多时刻测量的方法去除虚假点。多时刻定位算法能够定位至辐射源目标真实位置附近，然而精度受时差测量误差影响，难以得到较高的定位精度。而所提方法通过后续的逐点定位，在去除虚假点的基础上，能够大幅提高多时刻的定位精度。

5 结束语

三星时差定位通过两条时差线的交点确定干扰源位置，然而，若两条时差线存在两个交点时，则难以确定真实点位置。本文提出基于多时刻测量的虚假点消除方法。该方法利用多个时刻的时差测量数据判断干扰源真实位置所在区域，然后将该结果作为单时刻定位方程牛顿迭代方法求解的初始值，最终得到去除虚假点后高精度的定位结果。仿真实验分析了对定位性能的影响因素，验证了较大测量误差下和先验初始值偏差情况下的稳健性，实测数据处理结果验证了所提方法能够有效、快速地得到较高精度的定位结果。