基于HB加权函数的改进广义互相关算法

吴 慧，陈卫松

(安徽师范大学 物理与电子信息学院，安徽 芜湖241000)

0 引言

麦克风阵列声源定位技术，作为语音信号处理领域内的一项关键性技术，有着广泛的应用[1]。传统的声源定位技术主要包括：基于最大输出功率的可控波束成形法、基于高分辨率谱估计法和基于时延估计(Time Delay Estimation,TDE)的声源定位法[2]。相较于前两种声源定位算法，基于时延估计的声源定位算法实时性较好、计算复杂度相对较低且易于实现，因此得到了广泛应用[3]。

基于时延估计的声源定位方法主要包括广义互相关算法、自适应最小均方算法、互功率谱相位法、以及高阶统计量法等[4]。因为广义互相关算法原理较为简单，计算量较小，一直以来都受到很多研究人员的关注。早期的广义互相关时延估计的加权函数主要有平滑相干变换(SCOT)加权、相位变换(PHAT)加权、ROTH滤波器加权、最大似然(ML)加权和HB加权等[5-6]。近些年，唐娟等人将两路信号自相关和互相关的结果再做一次相关，得到二次相关函数，抑制了噪声的干扰[7]。茅惠达等人基于传统广义互相关时延估计，结合相关峰精确插值(FICP)算法，提高了相关函数的分辨率[8]。朱超等人提出了一种基于HB加权函数的广义二次相关希尔伯特差值时延估计算法，提高了时延准确度，但在低SNR情况受噪声干扰大[9]。张雷岳、刘超等人将PHAT加权与ML加权相结合，提出一种复合MLP加权函数，该算法增强了对环境噪声和混响的抑制，提高了时延估计的准确性[10]，但复合MLP加权算法的倒数是两加权函数的倒数之和，计算量会增加，降低了算法的实时性。

本文算法将SCOT加权函数和HB加权函数相结合，构成复合函数广义加权算法，该算法在接收信号信噪比不高于10 dB的情况下，能够获得较高的时延估计正确率，且算法稳定性也得到提高。

1 广义互相关时延估计算法

时延估计是利用两路接收信号的互相关函数来估计时间延迟，假设接收信号分别为x(n)和y(n)，在无混响的条件下，x(n)和y(n)可表示为：

x(n)=s(n)+vx(n)，

(1)

y(n)=s(n-D)+vy(n)，

(2)

式中，s(n)表示接收到的声源信号，v(n)表示阵元接收信号时产生的加性噪声，D表示两个接收信号之间的时间延迟。信号x(n)和y(n)的互相关函数Rxy(τ)可表示为：

Rxy(τ)=E[x(n)y(n-τ)]，

(3)

从而得到时间延迟的估计值为：

(4)

为了克服基本互相关算法在低信噪比情况下时延估计估计误差较大的缺点，Knapp和Carter提出了广义互相关函数的时延估计算法[11]，如图1所示。算法先对两路接收信号分别进行快速傅里叶变换(FFT)，得到两路信号互相关函数的频域形式，然后在频域对互相关函数进行加权计算，得到互功率谱密度函数，将加权计算后得到的结果进行快速傅里叶逆变换(IFFT)，转换成时域形式并进行峰值检测，将互相关函数峰值对应的时延值作为两个接收信号的时延差值。

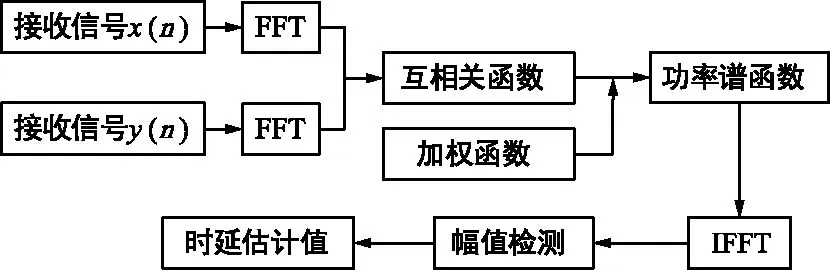
图1 广义互相关时延估计算法原理图Fig.1 Schematic diagram of generalized cross correlation time delay estimation algorithm

图1中互相关函数的计算过程可表示为：

(5)

式中，Gxy(ω)为信号x(n)和y(n)的互功率谱函数，Sxy(ω)为广义互相关加权函数。在时延估计过程中，选取不同的加权函数来针对不同类型的干扰，可以有效地抑制噪声或是混响干扰，从而提高时延估计精度，因此选择合适的加权函数，对于提高时延估计算法的性能有重要意义。

2 基于平滑相干HB加权函数的改进算法

2.1 改进算法原理分析

广义SCOT加权函数的表达式为：

(6)

该加权函数同时兼顾两路接收信号，克服了相关函数峰值拓宽而产生虚假峰值的影响。但当两路信号的功率谱密度相等时，会拓宽相关函数的峰值，产生虚假峰值而导致错误估计。

广义HB加权函数的表达式为：

(7)

该加权函数对互功率谱密度除以两个接收信号的自功率谱密度，以输入信号的自功率谱进行归一化处理，起到对输入声源信号预白化滤波的改进作用。除此之外，该加权函数与声源信号的互功率谱密度函数做乘积，增强了信号功率谱密度中声源信号的有用成分，因此整个加权函数的误差可以减小。

以上两种加权函数在低信噪比的时候，算法性能急剧下降，为了改善时延估计算法在低信噪比情况下的性能，本文提出一种改进的广义联合加权函数，记为SCOT-HB复合加权算法。加权函数表达式为：

(8)

式中，Sxx(ω)和Syy(ω)分别为信号x(n)和y(n)的自功率谱，Sxy(ω)为信号x(n)和y(n)的互功率谱。为了提高信号中高信噪比部分的能量，抑制低信噪比部分的能量，在加权函数分子项加入模平方相干函数|γxy(ω)|2，其表达式为：

(9)

模平方相干函数包含两路语音信号的互相关，在信号较小时，权值相应减小，噪声得到抑制。其中0≤α≤1，为常系数，其作用是控制模平方相干函数的强弱。由于加权函数在信号能量微弱时分母会接近零，使得该加权函数很大产生较大误差，所以在加权函数分母项加入一个常数β，且β≥0，以保证分母不会趋近于零，达到控制算法误差的目的。

忽略参数α和β，式(9)代入式(8)可简化为：

φSCOT(ω)·φHB(ω)，

(10)

因此改进算法从本质上看是对广义SCOT加权函数和广义HB加权函数的一种联合加权。

2.2 改进算法性能分析

为了对比分析广义SCOT加权函数、广义HB加权函数以及SCOT-HB联合加权函数的互相关时延估计波形性能。选取TIMIT标准库里TEXT测试库里编号为FAKS0-SA2.WAV的语音，信号采样频率为16 000 Hz，每帧采样点为600，帧移同帧长为600，仿真选取第45帧，延时点数为20。仿真计算不考虑混响的影响，添加的噪声为高斯白噪声。

如图2所示，当信噪比SNR=5 dB时，广义SCOT和广义HB加权函数都可以准确估计出时延值，但次峰幅度较大、对峰值的干扰明显，本文算法SCOT-HB的互相关函数峰值更尖锐、次峰幅度较小。

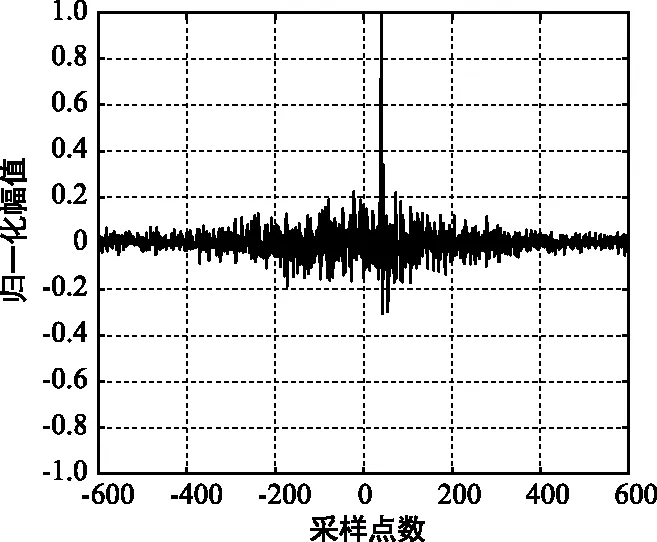
(a) SCOT互相关

(b) HB互相关

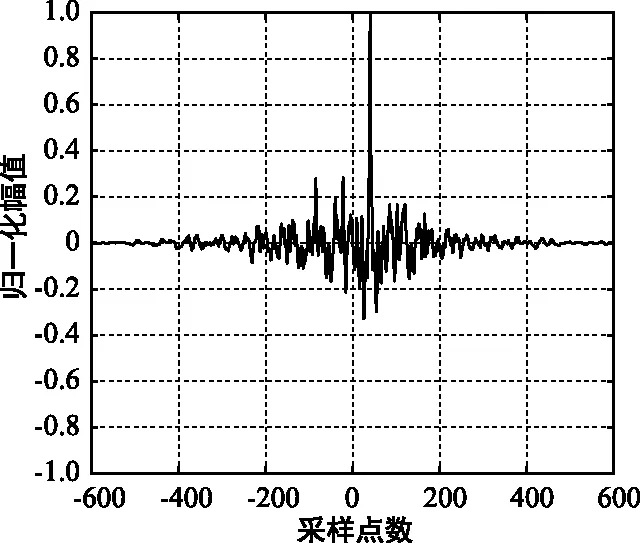
(c) SCOT-HB互相关

当信噪比降低到SNR=0 dB时，如图3所示，广义SCOT和广义HB加权函数时延估计均受次峰的干扰严重，不能准确的估计出时延值，而本文算法SCOT-HB仍具有较大的峰值、且次峰干扰较小。

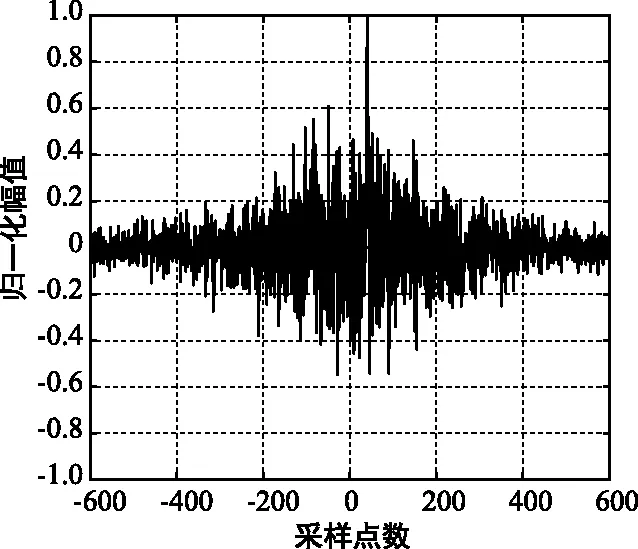
(a) SCOT互相关

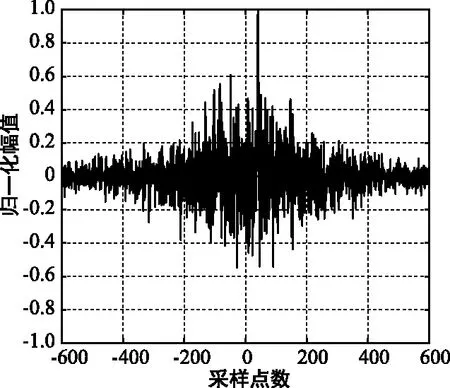
(b) HB互相关

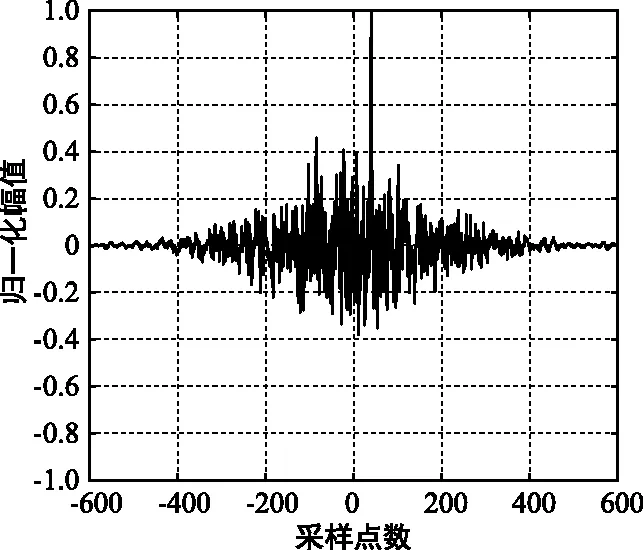
(c) SCOT-HB互相关

以上仿真结果表明，SCOT-HB联合加权函数相较于广义SCOT加权函数和广义HB加权函数，可以明显地抑制互相关函数的次峰干扰，突出互相关函数的主峰值，在较低的信噪比条件下能更准确估计出时延值，进而提高时延估计的正确率。

为了更加清楚的分析本文算法SCOT-HB联合加权函数的优势，对比分析广义SCOT加权函数、HB加权函数以及SCOT-HB加权函数三种算法随信噪比变化的归一化曲线，如图4所示。因为仿真中添加的是随机噪声，所以图4中每次仿真广义SCOT加权和广义HB加权的结果差别很大，但是相同条件下SCOT-HB加权的结果一直会处于一个平稳的变化中。所以本文算法把广义SCOT加权和广义HB加权相结合，不但更多的抑制了噪声，还提高了算法的稳定性。

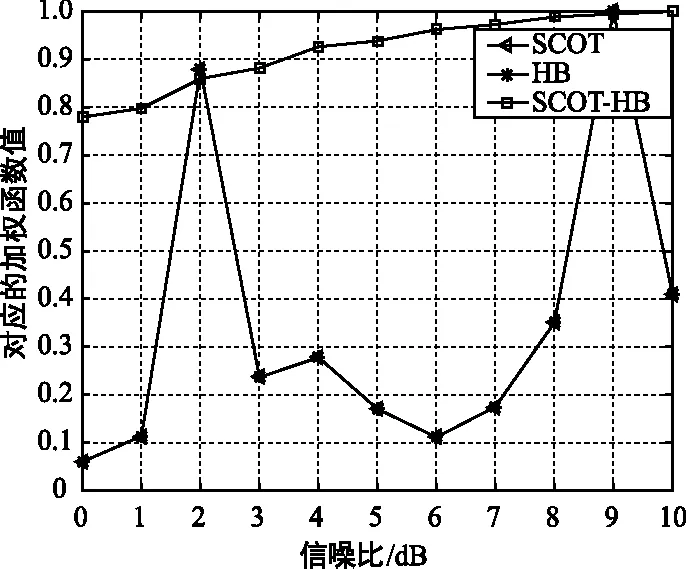
图4 3种加权函数随信噪比改变而改变的加权 函数的数值关系Fig.4 Numerical relationship of three weighting functions changing with signal-to-noise ratio

图4中广义SCOT加权和广义HB加权曲线重合，是因为来自同一声源的两路信号相关性较高，因此两种加权函数值的差别很小，仿真结果表明，当未归一化前的数据精确到小数点后第10位时，图4中广义SCOT加权和广义HB加权曲线才出现差异。

3 算法仿真分析

为了验证本文算法的时延估计性能，对本文算法进行Matlab仿真实验。信号源为TIMIT标准库里TEXT测试库内编号为FAKS0-SA2.WAV的语音，采样率为16 000 Hz，通过语音端点检测去掉无声段，每帧采样点为600，帧移同帧长为600，参与计算的帧数量为86帧，延时点数为20，信号中添加高斯白噪声。

关于参数α和β的取值，在存在噪声和混响的环境下对本文算法进行参数范围取值分析，仿真发现在不同语音信号、信噪比、平均次数、混响时间等环境下，当参数α在0.02附近、β在1.0附近取值时，算法的正确率较高、均方根误差值较小，因此仿真分析中选取α=0.02、β=1.0。

时延估计算法的性能通常用时延估计正确率NAC和均方根误差值σRMSE来衡量算法的估计精度和稳定性[12]。正确率的表达式为：

(11)

式中，Ncor为正确估计的次数，Nsum为总估计次数。均方根误差值的表达式为：

(12)

式中，τ0为真实时延值，τi为信号传播后的第i个时延值，N为时间延迟估计试验的总次数。

研究表明ML加权函数对于噪声干扰鲁棒性较强，PHAT加权函数对于混响干扰有较强抑制作用，复合MLP算法是对PHAT加权函数和ML加权函数的改进，弥补了原算法不能同时抑制噪声干扰和混响干扰的不足。该算法的表达式为[13]：

(13)

该算法中的q值大小对正确率的影响至关重要，而且在不同混响时间时所对应的q值也不一样。仿真中q的最优值为0.5。MLP算法从本质上看是对广义PHAT加权函数和广义ML加权函数的一种复合加权。

在不同的信噪比下，每帧信号做50次仿真，得出峰值对应的延迟点数，根据峰值对应的延迟点数取平均值。由于选取的信号源采样率不高，对时延估计的精度有一定影响，因此误差率设定为20%，即时延估计值和时延真实值之间偏离在4个采样点以内，则认为结果在误差率允许范围内，视为一次正确估计，时延估计正确率如图5所示。

图5 时延估计正确率随信噪比变化比较Fig.5 Comparison of time delay estimation accuracy with signal-to-noise ratio

从图5可以看出，随着信噪比逐渐提高，几种算法的时延估计正确率都在逐渐增加。本文算法的时延估计正确率最高，信噪比在5 dB时，比另外两种算法的正确率高20%左右。MLP算法的正确率不如HB加权算法，是因为MLP算法的合适应用场景是噪声和混响都存在的情况，而上述仿真没有加入混响。

对语音信号分别进行N=50次不同算法仿真，比较信噪比在0～10 dB时不同算法的均方根误差值，仿真结果如图6所示。

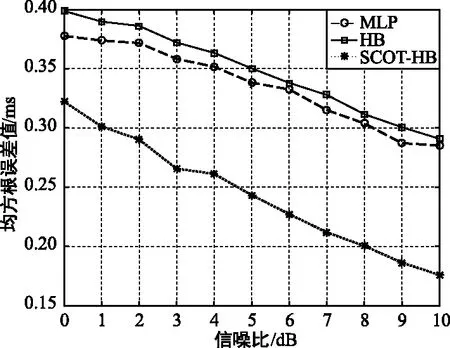
图6 时延估计均方根误差值随信噪比变化比较Fig.6 Comparison of root mean square error of time delay estimation with signal-to-noise ratio

从图6可以看出，随着信噪比逐渐提高，几种算法的时延估计均方根误差值都在逐渐减小。本文算法的均方根误差值最小，时延估计稳定性最好，信噪比为5 dB时本文算法的均方根误差值在0.25 ms左右，而另外两种算法的均方根误差值在0.35 ms左右。HB加权函数的均方根误差值最大，时延估计稳定性最差，MLP算法的均方根误差值次之。

考虑混响环境下的仿真，混响仿真环境与上述仿真环境一致。混响模型采用Allen和Berkley等人提出的镜像源模型(ISM)[14-15]。房间尺寸为[6.0 m4.0 m3.0 m]，两个麦克风的坐标分别为[0.8 m1.5 m1.5 m]和[1.9 m1.5 m1.5 m]，声源位置为[2.1 m2.2 m2 m]。当混响时间为0.5 s时，几种算法的时延估计正确率变化如图7所示，均方根误差值变化如图8所示。

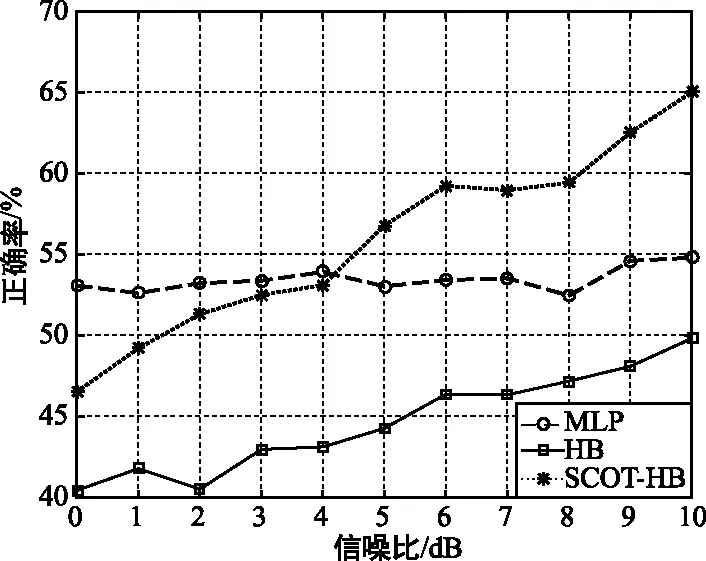
图7 混响时间为0.5 s时时延估计正确率随信噪比变化Fig.7 Comparison of time delay estimation accuracy with signal-to-noise ratio when reverberation time is 0.5 s

从图7可以看出，混响条件下，随着信噪比逐渐提高，几种算法的时延估计正确率都在逐渐增加，在0～10 dB时HB加权函数的时延估计正确率不高于另外两种算法。本文算法的时延估计正确率在信噪比高于4 dB时较另外两种算法好，MLP算法在信噪比低于4 dB时正确率最高，但随着信噪比增加正确率不如本文算法。

如图8所示，混响条件下，随着信噪比逐渐提高，几种算法的时延估计均方根误差值都在逐渐减小，在0～10 dB时HB加权函数的均方根误差值最大，时延估计稳定性最差，MLP算法的时延估计稳定性次之，本文算法的均方根误差值最小，稳定性最好。

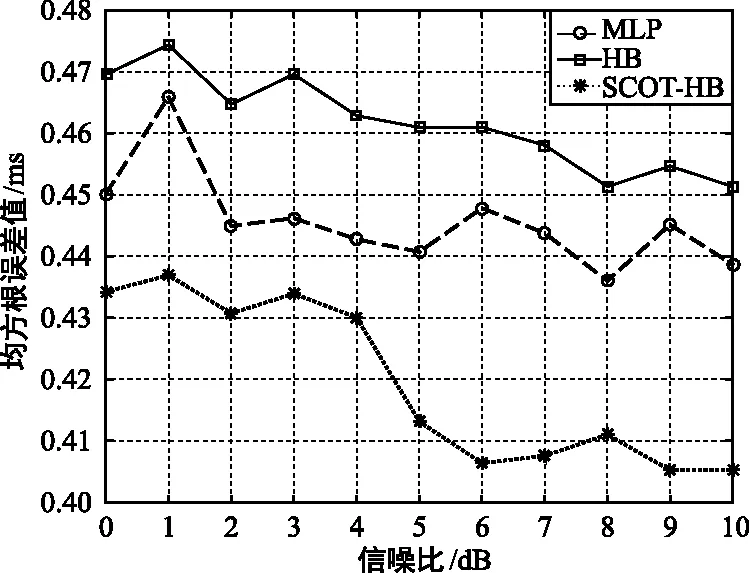
图8 混响时间为0.5 s时时延估计均方根误差值 随信噪比变化Fig.8 Comparison of root mean square error of time delay estimation with signal-to-noise ratio when the reverberation time is 0.5 s

4 结束语

在低信噪比环境下，广义互相关时延估计算法时延估计正确率减小、均方根误差值增大，为了提高算法性能，本文提出一种复合加权广义互相关时延估计算法，将SCOT加权函数和HB加权函数相结合。仿真结果表明，在信噪比不高于10 dB的低信噪比情况下，本文算法与复合MLP加权算法相比计算量更少，时延估计的稳定性也有所提升，正确率可以提高20%左右；甚至在信噪比不高于5 dB的情况下，正确率依旧可以提高18%左右，但在混响存在的条件下，本文算法的均方根误差值高于MLP加权算法。