基于李群的无迹卡尔曼滤波视觉SLAM算法
2022-04-01黄秀珍伍一帆李凯涛
黄秀珍,伍一帆,李凯涛
(1.浙江理工大学 科技与艺术学院,浙江 绍兴312369;2.杭州中威电子股份有限公司,浙江 杭州310000)
0 引言
如今,机器人的应用空间已走出实验室面向各个领域,小到日常生活中的家用吸尘器、快递分拣机等,大到国家领域中的深海采矿集矿机、无人机侦察等[1]。
在移动机器人领域,根据给定的环境地图有效确定所处位置是一项基本任务,但在缺少地图的情况下,机器人将无法进行自主定位[2]。机器人可以通过携带传感器来获取地图以及估计自身位置和姿态。最常见的方法是结合卫星信号完成位姿估计,但是卫星导航容易受到环境的影响,出现较大误差。而机器视觉SLAM算法可以搭载视觉传感器的主体,在没有环境先验信息的情况下,在运动过程中建立环境的模型,同时估计自己的运动[3]。因此视觉SLAM算法具有很高的研究价值,也是目前机器人视觉的研究热点。
基于滤波器的后端视觉SLAM定位算法最早出现于2002年,Davison等人[4]开始着手研究完整的视觉SLAM定位系统,实现了迭代扩展卡尔曼滤波(IEKF)的实时视觉SLAM系统,该研究首次建立了包含预测和噪声模型的视觉SLAM系统。现在人们以传统卡尔曼滤波(KF)算法为基础,涌现出大批基于扩展卡尔曼滤波、无迹卡尔曼滤波(UKF)和粒子滤波的位姿估计算法[5-6]。G.Loianno等人提出一个基于李群SE (3)的 UKF的视觉惯性里程计系统,以获得一个独特的、无奇异性的刚体姿态表示(SE(3)-UKF算法)[7]。Martin Brossard等人把视觉惯性和基于李群的无迹卡尔曼算法相结合[8],提出了L-UKF-LG算法和R-UKF-LG算法。本文以文献[8]的算法为基础,把UKF的系统状态用李群表示,并构建视觉惯性紧耦合模型,对文献[8]的算法进行改进,并在Matlab环境下对传统UKF算法、传统IEKF算法、SE(3)-UKF算法、L-UKF-LG算法和R-UKF-LG算法进行仿真分析。
1 UKF-LG视觉SLAM算法设计
本次仿真实验算法优化了传统UKF的系统状态,采用了UKF-LG视觉SLAM算法。算法通过视觉传感器对数量固定的三维路标进行观测,设定路标不随机器人的移动而产生变化,并采用惯性传感器(IMU)观测值和视觉测量值融合的方法解决了视觉惯导工作频率不一致的问题,构建视觉惯性紧耦合模型[9]。下面将分别介绍视觉惯性紧耦合模型、系统状态模型以及UKF-LG视觉SLAM算法流程。
1.1 视觉惯性紧耦合模型
视觉惯性紧耦合模型如图1所示,IMU提供机器人当前时刻的线加速度和角加速度信息,相机提供路标点的观测信息。系统状态模型中的位姿信息需要对IMU数据计算得到的估计结果以及相机的观测结果,并通过滤波器来得到最优的估计结果,UKF-LG算法对应于图中的“滤波器”部分。另外,IMU输出信息的速度和相机输出图像信息的速度并不是保持一致的,为了解决这一问题,设定IMU的信息输入周期为滤波周期[10]。如果当前时刻只有IMU信息输入,则紧耦合模型仅使用IMU的数据进行状态估计和更新;如果图像信息和IMU数据一起输入,则紧耦合模型将两个信息融合进行滤波,估计系统状态并更新。

图1 视觉惯性紧耦合框架Fig.1 Visual inertial tight coupling frame
1.2 系统状态模型
对于一个装载了IMU和视觉传感器的机器人,想要得到它的位姿信息,就需要估计它的旋转矩阵R、速度v、位移x、IMU偏差bk=[wk,b,ak,b],以及空间中的n个路标在世界坐标系下的位置信息y=[y1,y2,…,yn][11],具体的系统状态模型为:
(1)
式中,旋转矩阵R(k)表示从IMU坐标系到世界坐标系的变化,wk,i和ak,i表示k时刻IMU输出的角速度和线加速度,gG表示当前位置的重力加速度,dt为测量周期。式(1)中的误差均设定为方差为0的高斯白噪声:
n=[nw,na,nbw,naw]~N(0,Q)。
(2)
对于式(1)中的状态量,可以联合起来构成特殊欧式群矩阵Xk∈SE(3),特殊欧式群是一种李群,可以用来描述三维空间的旋转和平移,Xk的表示形式为:
(3)
特殊欧式群矩阵Xk不能进行欧式加法运算,只能采用指数映射的计算方式,而IMU偏差bk满足欧式加法运算,所以把这两项写出分块矩阵的形式,系统的状态方程表示为:
[Xk,bk]=f(Xk-1,Uk-bk-1,n),
(4)
式中,Uk=[wk,b,ak,b]为k时刻IMU测量到的角速度和线加速度。
观测模型用来描述k时刻机器人自身位姿与观测到的路标之间的关系,所以只有在视觉传感器检测到了路标后才有观测方程[12],k时刻的观测方程中存放的是当前时刻所有特征点的空间信息。下面给出系统的观测模型,对环境中路标的观测值为Z(k),观测噪声为ny:
(5)
式中,K为相机的内参矩阵;RC和tc分别表示从IMU 坐标系到相机坐标系的旋转矩阵和平移量。
1.3 UKF-LG视觉SLAM算法流程
下面给出UKF-LG视觉SLAM算法流程。
1.3.1 预测阶段
① 首先计算在李代数空间上2k+1维(k的取值由[Xk,bk]的维数确定)的sigma点的分布,sigma点的计算公式如下:
(6)
取λ=3-k,计算权值:
(7)
(8)
③ 求协方差矩阵P-,具体步骤为:
(9)
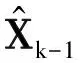
1.3.2 观测更新阶段
① 根据得到的协方差矩阵,重新计算sigma点:
(10)
(11)
(12)
1.3.3 滤波更新阶段
① 计算卡尔曼增益Kk:
(13)
(14)
2 UKF-LG视觉SLAM算法Maltab实现
2.1 初始参数说明
本次仿真使用的代码使用Euroc数据集[14],在Matlab2018b环境下仿真。对传统UKF算法、传统IEKF算法[15]、SE(3)-UKF算法、L-UKF-LG算法和R-UKF-LG算法进行对比仿真以验证算法准确度,视觉传感器的采集频率为20 Hz,IMU的采集频率为200 Hz。相机的校准矩阵如下:

(15)
2.2 算法模块框图
算法的整体流程分为四大模块:环境搭建、滤波法初始化、进行定位算法以及计算并显示误差。四大模板块的具体内容如下:
① 环境搭建:设置了相机的采样频率和IMU采样频率;读取数据集中通过相机拍摄的图片、相机位姿的真实值以及IMU数据。
② 滤波器初始化:协方差矩阵的初始化以及过程噪声和测量噪声的设置;系统状态的初始值以及相机的参数设置。
③ 进行定位算法:前文提到的几种滤波法的预测阶段、更新阶段、系统状态估计值的保存以及特征点集的更新。
④ 计算并显示误差:计算5种滤波法对机器人位置和姿态估计的标准误差(RMSE),并且绘制出曲线。主函数的流程图如图2所示。
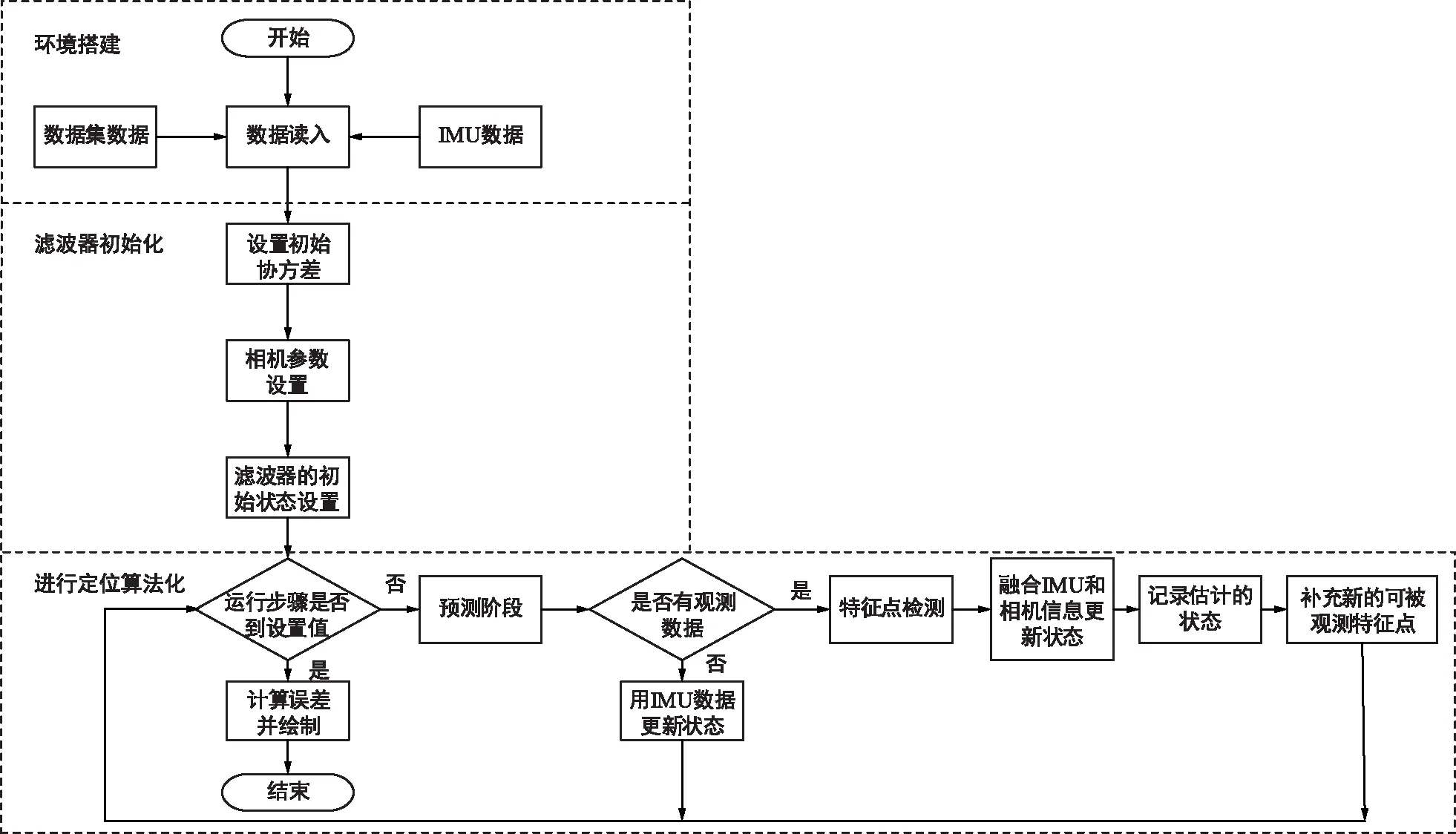
图2 主函数流程图Fig.2 Main function flow chart
图2中5个滤波法预测阶段的代码由**Propagation.m实现,其中的**表示对应的滤波法名称(比如L-UKF的m文件是lUKFPropagation);特征点检测的代码由ObserveLandmarks.m函数实现;状态更新阶段的代码和预测阶段类似,由**Update.m函数实现;记录估计的姿态由UpdateTraj.m函数赋值给各个滤波法的状态矩阵;特征点的补充由manageAmers.m函数运用线性三角形法实现。
3 仿真结果分析
为了比较5种滤波法在估计位姿上的性能,以5种滤波法对位置和姿态估计的均方根误差(RMSE)作为评价指标。数据集以微型飞行器作为载具,并配置了视觉惯性传感器在Vicon Room环境下采集数据,选择V1_02_medium数据集中的cam0进行仿真。
图3为在cam0数据集下5种滤波法在各个时刻对无人机的空间位置估计结果的误差,可以看处几种滤波器的位置误差差距并不是很明显。从图中可以看出,在整个时刻里,本文算法对于位置的估计要低于传统UKF算法,特别是在40~48 s后无人机发生大幅度的旋转(从数据集拍摄的视频可知)后,L-UKF-LG比其他滤波法能保持的误差更低。

图3 位置估计结果Fig.3 Location estimation results
图4为5种滤波法在cam0数据集下的姿态估计结果的误差。UKF花费了一定的时间才收敛在RMSE=1附近;40~48 s后无人机发生的大幅度旋转对R-UKF-LG算法和IEKF算法的姿态比较结果RMSE产生了影响,数值明显上升;SE(3)-UKF虽然使用了李群来表示状态信息,但是没有使用IMU来提供包括角速度在内的各种关于位姿的物理量信息,导致产生的误差一直累计,所以它的姿态RMSE值随着时间上升。相对于位置的比较结果而言,L-UKF-LG算法的姿态RMSE误差比较小,特别是30 s以后,能很好地保持在0.6以内,收敛性比较好。
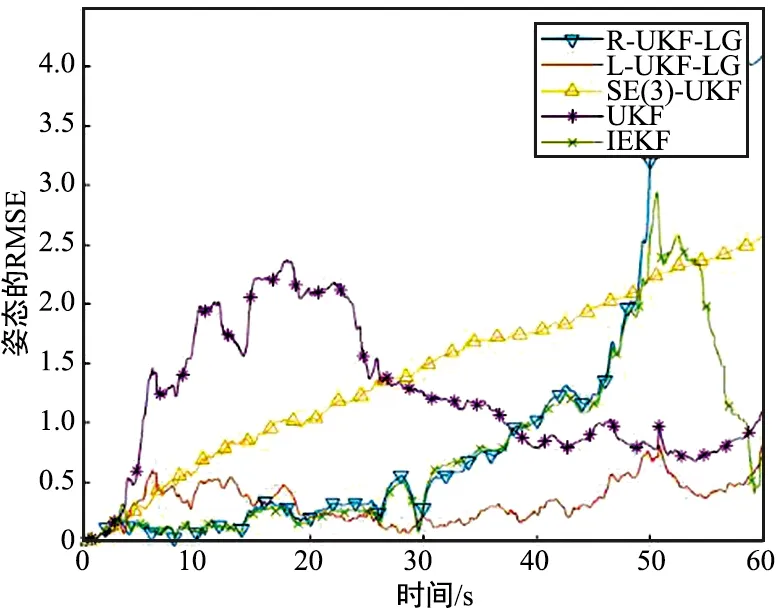
图4 姿态估计结果Fig.4 Attitude estimation results
4 结束语
本文实现了UKF-LG视觉SLAM算法,并构建视觉惯性紧耦合模型,在Matlab环境下实现UKF-LG算法,给出了5种滤波器在两个Euroc数据集中的仿真结果对比图。以RMSE为判断标准,分析了滤波器的定位性能,得出L-UKF-LG相对于传统的UKF算法,有更低的位置和姿态的RMSE,以及更好的定位精确性。本文中UKF对移动机器人的定位虽然取得了一定效果,但仍有很多的情况没有考虑,在状态向量初始值等参数的选择问题上还需要进一步研究和测试,找到能使算法性能达到最优或接近最优的参数组合。
