玻色-爱因斯坦凝聚态间的光学介导纠缠

高帅 PREST Matthew ILO-OKEKE Ebubechukwu O. KONDAPPAN ARISTIZABAL-ZULUAGA Juan E. IVANNIKOV Valentin BYRNES Tim

摘要： 着重研究了一种在玻色-爱因斯坦凝聚态（Bose-Einstein Condensate， BEC）之间产生光学介导纠缠的方案. 该方案使用量子非破坏性哈密顿量 ， 并将 BEC 置于马赫-曾德（Mach-Zehnder）构型中. 结果表明 ， 通过对光进行测量 ， 可以诱导产生纠缠态. 还特别分析了纠缠态在退相干作用下的效应. 研究表明 ， 该纠缠态的行为表现对于原子与光的作用时间较为敏感：当相互作用时间≲时 ， 该纠缠态相对稳定;当相互作用时间>时 ， 该纠缠态则相对脆弱.

关键词：玻色-爱因斯坦凝聚态;  量子非破坏性测量;  双自旋纠缠态;  退相干

中图分类号： O431.2    文献标志码： A    DOI：10.3969/j.issn.1000-5641.2022.02.011

Optically mediated entanglement between Bose-Einstein condensates

GAO Shuai1 ，  PREST Matthew1，2 ，  ILO-OKEKE Ebubechukwu O.2，3 ，  KONDAPPAN

Manikandan4     ARISTIZABAL-ZULUAGA Juan E.1，2 ，  IVANNIKOV Valentin1，5，6，7 ，

BYRNES Tim1，5，6，7

（1. State Key Laboratory of Precision Spectroscopy， East China Normal University， Shanghai  200241，China;2. Department of Physics， New York University Shanghai， Shanghai  200122， China;3. Departmentof Physics， School of Science， Federal University of Technology， Imo State  460001， Nigeria;4. Departmentof Precision Science and Natural Sciences， Institute of Physics， Universidad de Antioquia UdeA， Medellín05001000， Colombia;5. NYU-ECNU Institute of Physics at NYU Shanghai， Shanghai  200062， China;6. National Institute of Informatics， Tokyo  101-8430， Japan;7. Department of Physics， New YorkUniversity， New York， NY  10003， USA）

Abstract： This paper explores a method for generating optically mediated entanglement between Bose- Einstein condensates （BECs）. Using a quantum nondemolition Hamiltonian with BECs placed in a Mach- Zehnder configuration， it is shown that entangled states can be induced by performing measurement on light. In particular， the effects of the entangled state in the presence of decoherence were analyzed. The behavior of the entangled state was found to be sensitive to the atom-light interaction time. The entangledstate is relatively stable when the dimensionless interaction time  ?   and relatively fragile when the time is greater.

Keywords： Bose-Einstein condensate;   quantum nondemolition measurement;   two-spin entangled state; decoherence

0  引言

量子纠缠[1-2]作为一种重要的物理资源 ， 被广泛地应用于量子信息[3-5]和量子计算[6-7]等任务中.纠缠是量子力学的核心内容之一 ， 因此如何产生多粒子纠缠态是一项重要的任务. 而这其中的关键是多粒子纠缠态必须能被视作纯单粒子能级 ， 玻色-爱因斯坦凝聚态（BEC）则恰好满足这样的条件. 最近人们越发对研究宏观系统中的量子机理感兴趣. BEC 是一种典型的介观系综 ， 它内部包含103个或更多原子 ， 并且具有高度的相干性. 鉴于以上优点 ， BEC 提供了一种在宏观尺度上观测纠缠的可能性. 最近有3 个研究小组[8-10]演示了 BEC 中的纠缠 ， 并证明了单个 BEC 的2 个空间区域之间存在纠缠. 但是 ， 目前还没有 2个独立的 BEC 之间纠缠的演示. 而本文所使用的光学介导方案则可以在 2个 BEC 之间产生纠缠 ， 因此本文方案具有重要的意义.

量子计量是原子系综的主要应用之一.使用自旋压缩态可以提高测量灵敏度， 甚至可以超过标准量子极限.事实上 ， 单原子系综中的量子相干态可以转换成自旋压缩态[11-12]. 根据海森堡不确定原理[13-15] ， 自旋压缩态可以减小特定测量方向的不确定度， 反过来又可以增加另一个反方向的不确定度.实验中， 已经成功地将这种方法用在光学系统中[15-17]. 类似的 ， 这種方法也可以用在本文考虑的原子系统中.在测量内部自旋能级时 ， 有许多不同的相互作用可以降低噪声[12，18-20]. 在 BEC 中， 实验中得到论证的有效压缩作用有单轴和双轴反扭转哈密顿量[21-23] ， 这样的相互作用广泛应用于量子计算 [24]、计量 [25]、密码学[26] ， 以及引力波探测[27].

一般地 ， 真实的量子系统不可避免地与周围环境产生相互作用 ， 此时量子系统会变得非常脆弱 ， 而且非常容易失去相干性 ， 这就是常说的退相干[28]. 这是实现量子信息处理和量子计算的重大障碍. 因此研究量子系统的退相干机制 ， 以及如何在最大程度上抑制退相干是量子信息学中难以忽视的问题 .基于上述原因 ， 本文研究了纠缠态在退相干机制下的鲁棒性 ， 这将给相关量子逻辑门的设计提供可靠的量子比特来源 ， 并促进相应技术的发展.

1  物理模型

1.1  理论模型

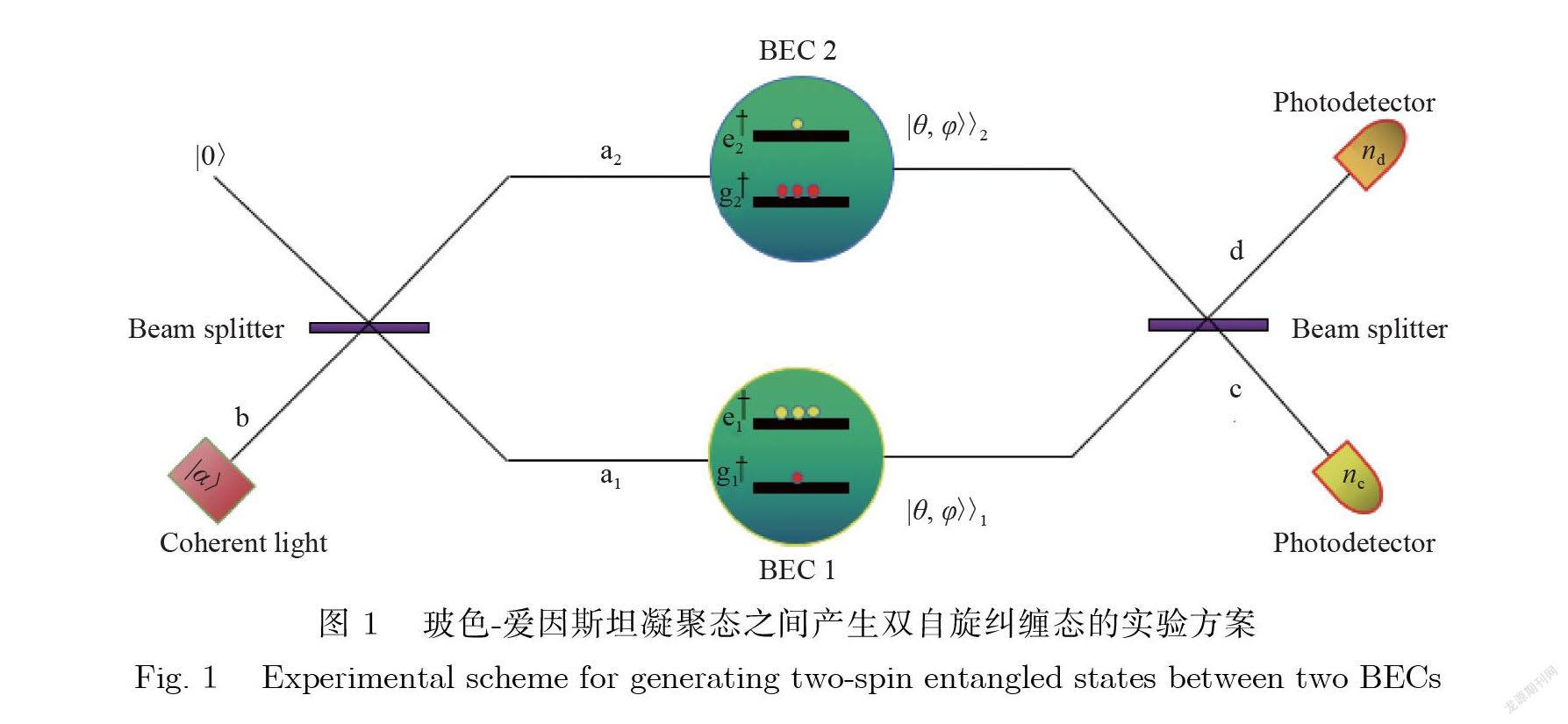
简化的2 个 BEC 之间产生纠缠的物理实现装置见图 1. 图1中 ， Coherent light 代表的是相干光源 ， Beam splitter 代表分束器 ， 光子数探测器则用 Photodetector 进行表示.该方案包含2个放置在马赫-曾德干涉仪（置于相干光路中） 的不同臂的、空间分离的 BEC.光与 BEC 通过量子非破坏性 （Quantum Nondemolition， QND）哈密顿量相互作用. 随后 ， 使用光电探测器对相应的光子数进行探测 ， 最终得到一个结构丰富的纠缠态. 这里考虑的 BEC 位于2个分离良好的阱中.此处的阱可能是原子芯片上分离的2 个磁阱 ， 也可能是光学偶极阱[29-31]. 每个 BEC 都有2 个可以布居原子的内部能级 ， 相应的玻色湮灭算子为 gj ， ej ， 其中 j ∈{1， 2}. 常见的内部能级态是超精细基态 ， 例如87Rb 的 F =1， mF = 1和 F =2， mF = 2时钟态[8，32-33].

为了推导的方便 ， 采用施温格（Schwinger）玻色算符定义有效自旋 ， 即

其中 ， j ∈{1， 2}用来标记 BEC.自旋算符遵循对易关系[Sl ， Sm]= 2iϵlmnSn ， 这里 l， m， n ∈{x， y， z} ， x， y， z 表示3 个坐标轴方向 ， ϵlmn 是完全反对称 Levi-Civita 张量.这里我们考虑每个 BEC 中的原子数是常量的情况 ， 因此有

（2）

这里原子数算符是福克（Fock）态的本征值 ， 可以记作

其中， Fock 态可以表示为

（4）

公式（4）中， |vac⟩是没有原子和光子的真空态. 通常用自旋相干态来描述 BEC， 其形式为

（5）

其中， 0⩽ θ⩽ π， −π⩽ φ⩽ π是布洛赫（Bloch）球上的2 个任意球坐标角. 具体推导过程如下.

2种不同光学模式的光束和各自的 BEC 相互作用.模式 b 是激光最初照射光束的玻色湮灭算符.该模式进入分束器 ， 进而转换成

通过2 个 BEC 的光束的玻色湮灭算符是 a1 ， a2. 光学模式的斯托克斯（Stokes）算符可以表示成

（7）

其中 np 是光子数算符.在光和 BEC 干涉后 ， 第二个分束器进一步对光学模式进行转换 ， 最后得到的相应光学模式的玻色湮灭算符 ， 用 c， d 进行表示. 该转换关系为

（8）

光子数算符的本征态 ， 可以表示为

（9）

其中 b 是相应光束的光学模式的湮灭算符.

光的初始态可以用光学相干态表征 ， 为

（10）

原子和光通过量子非破坏性（QND）哈密顿量相互作用 ， 该哈密顿量形式为

其中 ， Jz是描述光源的斯托克斯算符 ， S 和 S 是描述原子系统的施温格玻色算符.注意到[H，Jz]= 0 ， 这说明Jz没有时间依赖 ， 该哈密顿量确实是非破坏性的. 最后对光子数进行测量.

1.2  QND 纠缠方程

对于 QND 诱导纠缠的分析 ， 通常采用 Holstein-Primakoff （HP）近似

本文采用精确推导的方法 ， 这将允许用更长的时间尺度研究其行为模式. 这里考虑 BEC 的通用初始态

一种合适的初始态是2个偏振在Sx 方向的 BEC， 将其分别用自旋相干态表示 ， 易得

（14）

将其在 Fock 基中进行展开 ， 可以得到

（15）

激光将光学模式 b 映射成光学相干态 ， 因此光学初始态可表示为|α⟩b .在经过第一个分束器后， 初始波函数变为

其中 ， a1，a2是光学模式 b 经过分束器后所产生的新光学模式.随后光和 BEC 产生相互作用 ， 假设该相互作用时间为 t， 则相互作用后的初始态演化为

|ϕ（τ）⟩= e −  |ϕ（0）⟩= exp [−  （S − S ）Jz]|ϕ（0）⟩.     （17）

这里定义无量纲时间τ≡ Ωt .将式（13）带入式（16）， 得到

（18）

下一步应用公式（8）的分束算符， 初始态演变为

最后， 分别探测在光学模式c， d 下的光子数 ， 这等价于将式（19）用测量算符进行投影 ， 有

（20）

忽略不相关的全局相位 ， 未归一化态为

（21）

其中， Fock 基下的系数Cnc nd （χ）具有

该式可由

（23）

进行归一化.

公式（21）给出的形式表明 ， 该光介导方案的效应是非常简单的 ， 最初的波函数被一个额外因子 Cnc nd  [（ k1 − k2）τ] 所调制. 在测量光子数后 ， 归一化纠缠态的波函数为

（24）

这里归一化因子等价于光子探测概率

（25）

公式（24）是我们最终求得的2 个 BEC 之间的波函数. 显然 ， 公式（19）的形式表明 ， 初始光学态的取值可以是任意的. 精确波函数表达式（21）适用于任意时间 ， 从而大大扩展了模型的适用范围.

1.3  近似分析

在获得了波函数精确表达式后 ， 为了直观研究该纠缠态的性质 ， 我们对其进行了近似分析. 这里研究较短的相互作用时间τ≲  ， 因为该区域是产生 BEC 间纠缠的最相关区域 ， 且适合近似分析.

首先， 当 N ≫1时 ， 可以将二项式系数近似为

（26）

可以看出 ， 只有在 −  ≲ k1， k2 ≲  +范围内的 Fock 项 ， 其系数才有明显的权重 ， 这也导致了波函数（21）系数产生了不均匀叠加.

如果总光子数 Np ≫ 1 ， 可以进一步对式（21）做斯特林（Stirling）近似[34] ， 可以得到高斯（Gauss）型函数

（27）

其中nc 是探测到的 c 光学模式下的光子数. 在较短时间内 ， 事实上 ， 光子数大多集中在模式 c 上 ， 所以我们选取参数nc = Np， nd = 0. 从公式（27）可以明显得到 ， 最大值发生在

（28）

由于余弦函数的振荡性质 ， 它通常具有k1 ， k2的多个解.

事实上 ， 还可以直接对余弦函数进行指数近似.此时不需要限定 Np ≫ 1 ， 只需保证时间较小即可 ， 便得到这样的近似

（29）

综合公式（26）和式（29）， 最终公式（21）的波函数近似为

（30）

该近似对于 N ≫1， |τ| ≲  ， |α|≫ 1有效.这里 ， N 是归一化系数 ， 为

此近似的概率分布为

其中， k1， k2是 2个 BEC 在 Fock 态下的表示模式.从公式（32）可以看到， 纠缠脉冲在k1， k2两个模式间产生了关联. 公式（32）的第一项是个对称的非关联高斯分布 ， 平均值⟨k1， k2⟩=  ， 标准差为; 第二项则产生了关联并导致了最后的纠缠. 也可以看到 ， k1 = k2的情况概率分布最明显 ， 且关联的强度和无量纲的时间τ以及光子数nc 有关. 为了产生强关联 ， 式（30）表明， 相互作用时间τ应该满足

（33）

联想到时间τ≲  ， 可以得到关系式

所以， 这说明使用明亮的相干光 ， 可以帮助产生 BEC 之间的更强关联.

2  结果与分析

在得到双自旋纠缠态的波函数表达式（21）后 ， 对其概率密度分布进行研究 ， 可以对其性质有更好的认识. 另一方面 ， 通过施加马尔可夫退相干作用 ， 研究该纠缠态在不同时间尺度下的行为特征及鲁棒性， 这将有助于其在量子信息以及未来的量子计算方面的应用.

2.1  概率密度分布

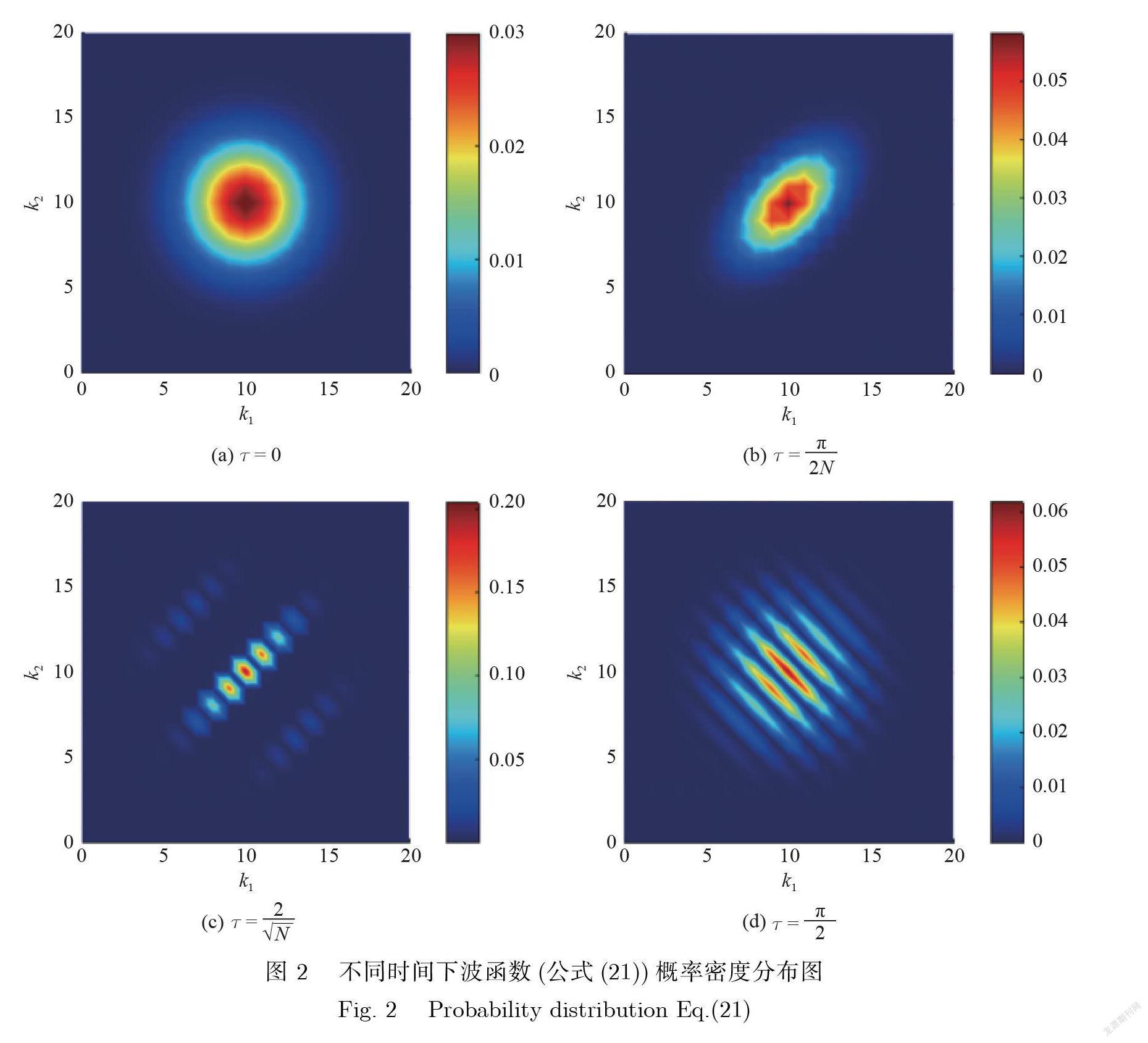
图 2给出了不同时间下的雙自旋纠缠态（公式（21））的概率密度分布.横坐标k1是第一个 BEC 在 Fock 态下的表示模式 ， 纵坐标k2是第二个 BEC 在 Fock 态下的表示模式.通过概率分布 ， 可以直观地分析2 个 BEC 之间的关联状态. 所采用的参数：原子数 N =20; 光子数nc = 20; 光子数nd = 0; α=     =  .

从图 2（a）可以看到 ， 在τ= 0时 ， 概率分布呈现高斯分布 ， 且中心处于k1 = k2 =  .这是非常容易理解的：考虑到当τ= 0时 ， 没有施加相互作用 ， 此时就是两个自旋相干态（式（14））.该纠缠态继续演化 ， 直到时间在图 2（b）的τ=  尺度时 ， 明显地观察到压缩现象 ， 方向沿着k1 = k2 ， 这完全符合公式（32）所表达的内容.事实上 ， 图 2（b）的概率分布和双模压缩态的概率分布是一致的 ， 这说明初始态经过τ=  的演变后 ， 已演变成双模压缩态. 继续增加时间τ ， 当τ= 时 （图 2（c））， 此时观察到更大程度的压缩和更强的关联 ， 并在主关联峰旁边出现了两个副关联峰. 当时间来到图 2（d）的τ= 时 ， 出现了更多的多关联峰 ， 这意味着波函数出现了非高斯行为模式 ， 同时也意味着 Holstein-Primakoff （HP）近似的瓦解. 这足以体现本文采用的精确推导的方法的优越性. 因为我们可以在更长的时间下研究态的演化. 全面对比图 2的4 幅图 ， 不难看出 ， 单关联峰和多关联峰分布的分界线是在τ=  ， 即τ∼级别上.

事实上 ， 之所以会出现多关联峰 ， 这是由于公式（28）中三角函数的周期性引起的：由于 n 取值的多样性（n =0， ±1， ±2， ±3， ·· ·）， 因此可以有多组 k1 − k2满足条件. 而对于时间分界线的出现 ， 这可以从公式（26）得到解释：由于只有在 −  ≲ k1， k2 ≲  +范围内的 Fock 项 ， 其系数才有明显的权重.所以此时便有k1 − k2 ∼  .从公式（28）容易看出， 只有当时间τ∼  ， 才会出现2τ（k1 − k2）∼nπ ， 此时多关联峰效应才开始显著. 而在此之前 ， 则由于时间尺度太小 ， 超出了有效 Fock 态范围 ， 因此呈现单关联峰分布.

2.2  马尔可夫退相干

近似态（式（30））直观展示出了2 个 BEC 之间的纠缠 ， 然而这是没有考虑任何耗散的理想情况. 接下来 ， 将要探究马尔可夫退相干下纠缠态的演化 ， 该效应会显著影响原子系综里纠缠的大小.抑制退相干影响的能力 ， 是衡量纠缠方案价值的有力标准.在本文所述系统中 ， 退相干的物理来源是交流斯塔克（AC-Stark）效应和文献[35]所述的原子阱电流扰动. 退相干存在于任何系统中 ， 初始态密度矩阵可以写成

（35）

作为一个通用的退相干模型 ， 对每个自旋态施加马尔可夫退相干

（36）

这里考虑 j = z， x 的效应. Sz 退相干和 Sx 退相干是2种不同的退相干机制. 事实上 ， 由于林德布拉德（Lindblad）算符Sz 和 QND 哈密顿量对易 ， 我们可以在相互作用产生纠缠态后 ， 直接施加退相干效应 ， 这将仍然得到精确表达式.因此 ， 将马尔可夫退相干直接应用到波函数表达式（34）， 最终获得Sz 退相干精确密度矩阵 ， 其表达式为

其中， N1 =⟨ nc nd （τ） | nc nd （τ）⟩.

而对于Sx 退相干 ， 精准的求解方式是解公式（36）.但是在较短的时间内 ， 可以做一種近似分析 ， 即在获得波函数精确表达式（21）后 ， 在布洛赫（Bloch）球上对其进行旋转操作 ， 然后施加Sz退相干作用.

事实上 ， 从一个（ S − S ）哈密顿量开始计量纠缠 ， 最后施加Sx 退相干 ， 和从（ S − S ）哈密顿量开始然后施加Sz退相干的方式是等价的.在Sy 基中 ， 对于公式（21）做一个角度的旋转 ， 最后乘上退相干表达式 e −2Γτ [（k1−k ）2+（k2−k ）2]便可以得到 Sx退相干下的波函数 ， 也即

（38）

其中， N2 =⟨ϕk ，k  （τ） |ϕk ，k  （τ）⟩是归一化因子. ⟨k|e −iSy   |k′⟩由

（39）

给出.

最后， 得到Sx退相干下的密度矩阵 ， 其表达式为

（40）

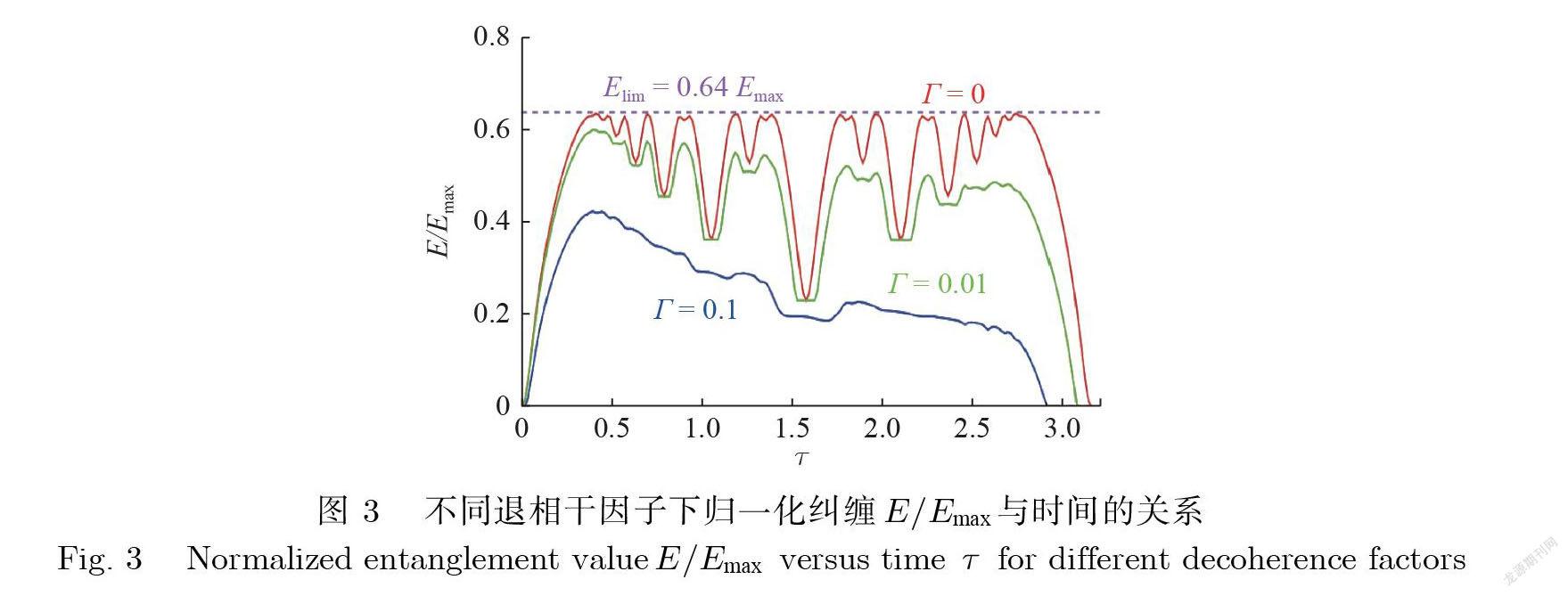
图 3 给出了施加马尔可夫退相干作用后， 不同退相干因子下， 归一化纠缠值与时间的关系 ， 其中 Emax 由公式（42）给出. 所采用参数： 原子数 N =20; 光子数 nc = 20; 光子数 nd = 0; α=  =  .

一般来说 ， 退相干会急速地破坏现有的纠缠. 对于纯态来说 ， 冯·诺依曼熵（von Neumann entropy）可以很好地量化纠缠. 由于退相干的存在 ， 原有的纠缠态演变成混合态 ， 更好的量化方式是对数负性[36-37]. 纠缠值的计算表达公式为

其中， ρT2是第二个 BEC 的部分转置. 可将纠缠值用最大纠缠值进行归一化 ， 即

（42）

在图3中 ， 在Γ =0 时 ， 纠缠展示出了一种魔鬼裂缝（devil’s crevasse）， 这和采用冯·诺依曼熵量化的纠缠所表现的行为相似.在文献[38]中 ， 纠缠展示出了分形扰动 ， 且纠缠结构图的周期为 .考虑到哈密顿量的相似性 ， 这可以非常容易理解.注意到一个典型的时间τ=  ， 在该时间点之前 ， 纠缠线性增加 ， 在该时间点后 ， 纠缠展现出复杂的谷状结构. 另一个特点是纠缠天花板 ， 这是由于二项式项不均匀叠加产生的 ， 它只包括中心在 k1， k2 =  附近∼ O（） 范围的 Fock 项. 因此限制了纠缠值并产生了纠缠天花板. 此外， 由于退相干效应 ， 归一化纠缠值随着退相干因子增加而变小.

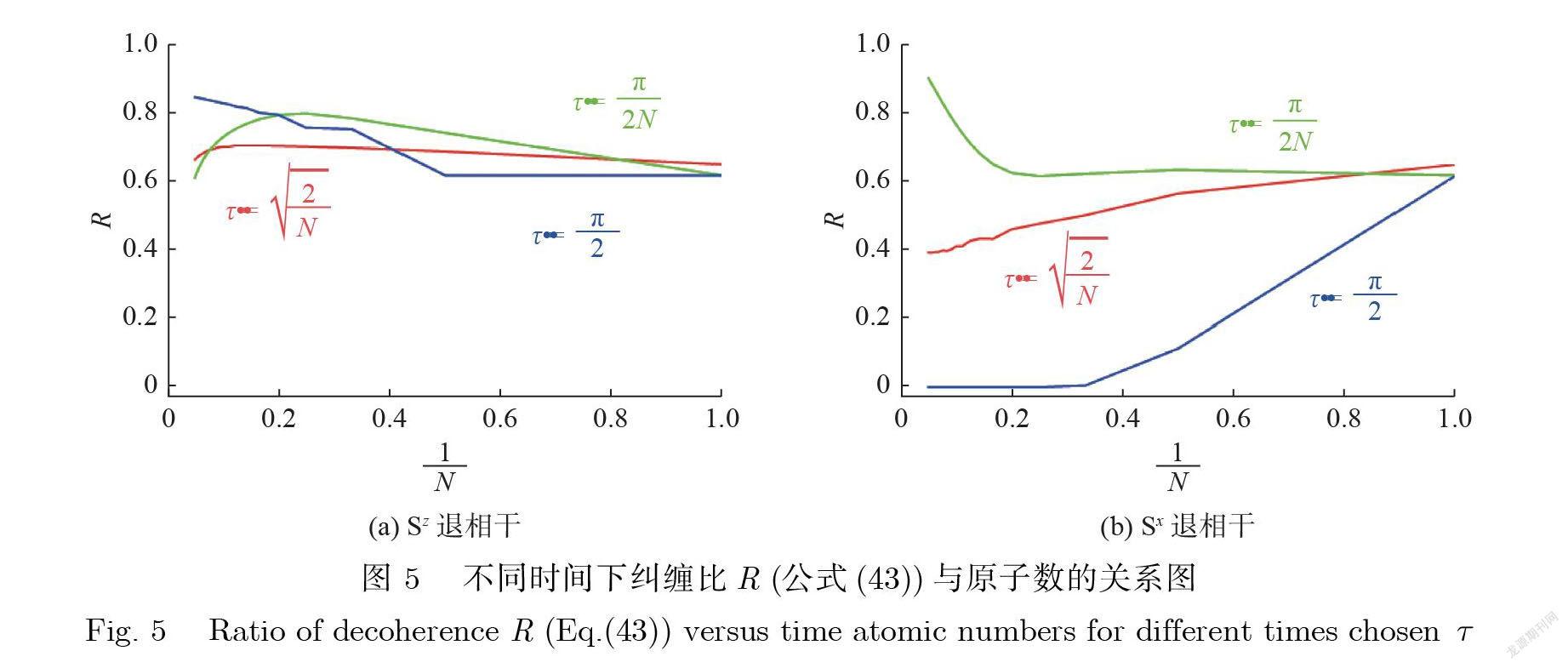
为了研究纠缠的特性 ， 这里选择了3 个典型的时间τ=  ，  ，   . 图4给出了Sz 和Sx 退相干方式下 ， 不同时间尺度纠缠值 E （公式 （41））与原子数的关系 .所采用参数：最大原子数 Nmax =20;光子数nc = 20; 光子数nd = 0; α=  =  ;Γz，x = 0.1. 图 5则给出了Sz 和Sx 退相干方式下 ， 不同时间尺度纠缠比 R （公式（43））与原子数的关系图. 所采用参数：最大原子数Nmax =20; 光子数 nc = 20; 光子数nd = 0; α=  =  .结合图 4和图 5， 很明显地可以观察到 ， 3种时间下纠缠行为差异十分显著.

在图4中 ， 图4（a）代表Sz 退相干方式 ， 而图4（b）代表Sx 退相干方式. 对于τ=  ， 纠缠值 E 与Γj = 0的情况对于原子数 N具有相似的依赖. 并且在 N →∞ 时 ， 纠缠比

（43）

趋向于1个常数（图5（b））.随着 N 增大， 由于相互作用门减小时间∝  .因此， 退相干能够作用的时间也随之减小 ， 两者得以抵消.

在τ=  时 ， 图 4中的纠缠逐渐增加.在图5中 ， 对于Sz 退相干（ 图5（a））， 纠缠比基本上是恒定的， 而对于Sx 退相干（ 图5（b））， 在 N →∞ 时 ， 纠缠比缓慢衰减到 R =0 .

关于时间τ= 的Sx 退相干 ， 纠缠迅速以～ e −N2依赖衰减（ 图4 （b））.对于Sx 退相干 ， 纠缠比也以指数形式衰减（图5（b））.这种高斯依赖是薛定谔猫态在退相干下的典型特征. 事实上 ， 在τ= 时 ， 波函数可以写成

（44）

值得注意的是 ， 对于时间τ= 的Sz 退相干 ， 随着原子数 N 的增加 ， 纠缠比 R 先保持常量后增加.考虑到主方程（36）的退相干自由子空间 ， 可以很容易理解[39]. 这里退相只改变量子位的局部相位 ， 随机相位并不会影响纠缠 ， 因为量子位之间的纠缠早已建立.

总结上面的分析：对于所有的3 个相互作用时间 ， 在施加Sz退相干效应时 ， R 和 N 有这样的关系其中， 0⩽ q <1 ;而对于Sx 退相干， 3种时间尺度表现出不同的行为模式

其中 ， 0< q <1 ， a =0.95569， b =0.790911， c =2.18937， d =0.293331， h =4.26138. 这表明如果退相干和哈密顿量在对易基上相互作用（Sz 退相干）， 2个 BEC 之间的纠缠可以足够稳定 ， 即使 N 非常大 ， 依旧如此. 综合两种退相干方式 ， 对于较短的时间尺度τ∼  ， 纠缠对于退相干表现得足够稳定. 对于更长的时间尺度τ∼ O （1） ， 由于薛定谔猫态的出现 ， 纠缠态会变的非常脆弱.这两种截然不同行为的分界时间线是τ∼  .这说明 ， 当τ⩽时 ， 纠缠态足够稳定并且适合实验观测.

可以看到 ， 对于Sz 退相干和Sx 退相干 ， 其行为表现存在着显著差异. 这的确是2 种不同的退相干方式.上述已经介绍了2 种退相干方式密度矩阵来源的不同.这里有必要其物理来源做出进一步的解释 .事实上 ， 这是源于不同的自旋算符对于 Fock 态具有不同的作用形式 ， 即

（47）

此处 Fock 态是 Sz算符的本征态. 容易看到 ， Sz算符不会对 Fock 态有移位作用 ， 而Sx退相干则会对 Fock 态产生移位作用（|k +1⟩ ， |k −1⟩）， 因此必然会造成退相干密度矩阵的不同. 这也最终导致了 Sx 退相干和Sz 退相干下， 该双自旋纠缠态的不同行为表现.

3  结论

本文主要研究了玻色-爱因斯坦凝聚态间的光学介导纠缠 ， 在马赫曾德干涉仪光路下， 利用光和原子的干涉 ， 通过精确推导 ， 得到了具体的波函数. 并进一步研究了其在不同时间下的概率分布.发现在较短的时间范围内 ， 该纠缠态呈现明显的压缩效应 ， 而当时间τ= 时 ， 出现了很多的关联峰 ， 这表明非高斯行為的出现. 这种现象出现的原因 ， 是由于公式（28）中三角函数的周期性导致的.且出现单关联峰和多关联峰分布的分界线是在 τ= 即 τ∼级别上 .这是由于二项式系数限制了有效Fock 态范围 − ≲k1 ， k2 ≲  + ， 同时在公式（28）的多关联峰公式的双重作用下 ， 导致了只有τ ∼1/才开始观察到多关联峰. 本文还研究了在马尔可夫退相干作用下 ， 纠缠态在不同时间下的鲁棒性. 发现对于较短的时间尺度τ∼ 1/N ， 退相干对于纠缠态的影响较弱. 对于更长的时间尺度τ ∼ O （1） ， 由于薛定谔猫态的出现 ， 纠缠态会变得非常脆弱. 这两种截然不同行为的分界时间线是τ ∼  .对于Sz 退相干和Sx 退相干 ， 其行为模式差异显著 ， 这是由不同的自旋算符对 Fock 态具有不同的作用形式而导致的.本文工作可为量子测量和量子计算提供一种可靠的纠缠来源 ， 并通过对退相干的探究， 促进相应量子技术的发展.

[参考文献]

[1] NIELSEN M A， CHUANG I L. Quantum Computation and Quantum Information [M]. 10th Anniversary ed. [S.l.]： CambridgeUniversity Press， 2011.

[2] HORODECKI R， HORODECKI P， HORODECKI M， et al. Quantum entanglement [J]. Reviews of Modern Physics， 2009， 81（2）：865.

[3] BENNETT C H， BRASSARD G， CRÉPEAU C， et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels [J]. Physical Review Letters， 1993， 70（13）：1895-1899.

[4] EKERT A K. Quantum cryptography based on Bell’s theorem [J]. Physical Review Letters， 1991， 67（6）：661.

[5] BYRNES T， ROSSEAU D， KHOSLA M， et al. Macroscopic quantum information processing using spin coherent states [J]. OpticsCommunications， 2015， 337：102-109.

[6] BYRNES T， WEN K， YAMAMOTO Y. Macroscopic quantum computation using Bose-Einstein condensates [J]. Physical Review A，2012， 85（4）：4233-4237.

[7] GROVER L K. Quantum mechanics helps in searching for a needle in a haystack [J]. Physical Review Letters， 1997， 79（2）：325.

[8] FADEL M， ZIBOLD T， DÉCAMPS B， et al. Spatial entanglement patterns and Einstein-Podolsky-Rosen steering in Bose-Einsteincondensates [J]. Science， 2018， 360（6387）：409-413.

[9] KUNKEL P， PRÜFER M， STROBEL H， et al. Spatially distributed multipartite entanglement enables EPR steering of atomic clouds[J]. Science， 2018， 360（6387）：413-416.

[10] LANGE K， PEISE J， LÜCKE B， et al. Entanglement between two spatially separated atomic modes [J]. Science， 2018， 360（6387）：416-418.

[11] BYRNES T， ILO-OKEKE E O. Quantum Atom Optics： Theory and Applications to Quantum Technology [M]. [S.l.]： CambridgeUniversity Press， 2021.

[12] GROSS C. Spin squeezing， entanglement and quantum metrology with Bose-Einstein condensates [J]. Journal of Physics B， 2012，45（10）：103001.

[13] SØRENSEN A， DUAN L M， CIRAC J I， et al. Many-particle entanglement with Bose–Einstein condensates [J]. Nature， 2001， 409（6816）：63-66.

[14] MACHIDA S， YAMAMOTO Y， ITAYA Y. Observation of amplitude squeezing in a constant-current –driven semiconductor laser [J].Physical Review Letters， 1987， 58（10）：1000-1003.

[15] WU L A， KIMBLE H J， HALL J L， et al. Generation of squeezed states by parametric down conversion [J]. Physical Review Letters，1986， 57（20）：2520-2523.

[16] SLUSHER R E， HOLLBERG L W， YURKE B， et al. Observation of squeezed states generated by four-wave mixing in an opticalcavity [J]. Physical Review Letters， 1985， 55（22）：2409-2412.

[17] BREITENBACH G， SCHILLER S， MLYNEK J. Measurement of the quantum states of squeezed light [J]. Nature， 1997， 387（6632）：471-475.

[18] MACOMBER J D， LYNCH R. Squeezed spin states [J]. The Journal of Chemical Physics， 1985， 83（12）：6514-6519.

[19] WALLS D F， ZOLLER P. Reduced quantum fluctuations in resonance fluorescence [J]. Physical Review Letters， 1981， 47（10）：709-711.

[20] WODKIEWICZ K， EBERLY J H. Coherent states， squeezed fluctuations， and the  SU（2） am  SU（1，1） groups in quantum-opticsapplications [J]. Journal of the Optical Society of America B， 1985， 2（3）：458-466.

[21] KITAGAwA M， UEDA M. Squeezed spin states [J]. Physical Review A， 1993， 47（6）：5138-5143.

[22] MUESSEL W， STROBEL H， LINNEMANN D， et al. Scalable spin squeezing for quantum-enhanced magnetometry with Bose-Einsteincondensates [J]. Physical Review Letters， 2014， 113（10）：103004.

[23] HALD J， SØRENSEN J L， SCHORI C， et al. Spin squeezed atoms： A macroscopic entangled ensemble created by light [J]. PhysicalReview Letters， 1999， 83（7）：1319-1322.

[24] NAVARRETE-BENLLOCH C . Quantum information with continuous variables [M]// An Introduction to the Formalism of QuantumInformation with Continuous Variables.[S.l]：[s.n.]， 2015.

[25] MOXLEY F， DOWLING J， DAI W， et al. Sagnac interferometry with coherent vortex superposition states in exciton-polaritoncondensates [J]. Physical Review A， 2016， 93：053603.

[26] HILLERY M. Quantum cryptography with squeezed states [J]. Physical Review A， 2000， 61（2）：022309.

[27] BONDURANT R S， SHAPIRO J H. Squeezed states in phase-sensing interferometers [J]. Physical Review D Particles & Fields， 1984，30（12）：2548-2556.

[28] BREUER H P， PETRUCCIONE F. The Theory of Open Quantum Systems [M].[S.l.]： Oxford University Press， 2002.

[29] REICHEL J， VULETIC V. Atom Chips [M].[S.l.]： John Wiley & Sons， 2011.

[30] WHITLOCK S， GERRITSMA R， FERNHOLZ T， et al. Two-dimensional array of microtraps with atomic shift register on a chip [J].New Journal of Physics， 2009， 11（2）：023021.

[31] ABDELRAHMAN A， MUKAI T， HÄFFNER H， et al. Coherent all-optical control of ultracold atoms arrays in permanent magnetictraps [J]. Optics Express， 2014， 22（3）：3501-3513.

[32] BÖHI P， RIEDEL M F， HOFFROGGE J， et al. Coherent manipulation of Bose –Einstein condensates with state-dependent microwavepotentials on an atom chip [J]. Nature Physics， 2009， 5（8）：592-597.

[33] RIEDEL M F， BÖHI P， LI Y， et al. Atom-chip-based generation of entanglement for quantum metrology [J]. Nature， 2010， 464（7292）：1170-1173.

[34] ILO-OKEKE E O， BYRNES T. Information and backaction due to phase-contrast-imaging measurements of cold atomic gases： BeyondGaussian states [J]. Physical Review A， 2016， 94（1）：013617.

[35] LONE M Q， BYRNES T. Suppression of the ac-Stark-shift scattering rate due to non-Markovian behavior [J]. Physical Review A，2015， 92（1）：011401.

[36] VIDAL G， WERNER R F. Computable measure of entanglement [J]. Physical Review A， 2002， 65（3）：032314.

[37] PLENIO M B. Logarithmic negativity： A full entanglement monotone that is not convex [J]. Physical Review Letters， 2005， 95（9）：090503.

[38] BYRNES T. Fractality and macroscopic entanglement in two-component Bose-Einstein condensates [J]. Physical Review A， 2013，88（2）：023609.

[39] LIDAR D A， WHALEY K B. Decoherence-free subspaces and subsystems [M]// Irreversible Quantum Dynamics， Lecture Notes inPhysics， vol 622. Berlin： Springer， Berlin， 2003：83-120.

（責任编辑：李艺）