一种可重构有源滤波器芯片设计
2022-03-31余俊伟刁盛锡
余俊伟 刁盛锡

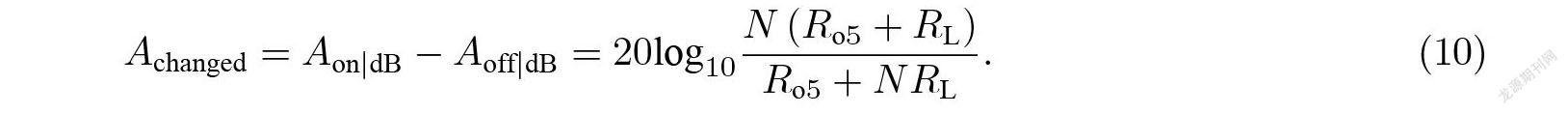
摘要: 近年来 , 多模多带收发机的研究成为了研究热点 , 而软件定义无线电系统是一个很好的候选方案. 为了减小带外干扰对软件无线电系统收发机性能产生的负面影响 , 提出了一个可调带宽、可调增益的高带外抑制中频滤波器①. 该滤波器由双二次 Gm-C 滤波器、增益提高级、5阶椭圆滤波器组成. 滤波器增益的调节通过双二次 Gm-C 滤波器和增益提高级实现 , 带宽的调节通过开关电容阵列实现. 同时 , 为了提高带外抑制 , 增加了一级5 阶椭圆滤波器. 后仿真结果表明 , 滤波器带宽在1 MHz ~30 MHz 可调 , 2倍带宽频率的带外抑制最小值达到了44.56 dB, 增益控制范围为–20 dB ~20 dB, 模拟部分的功耗和核心面积分别为 5.1 mW 和1.23 mm2. 提出的滤波器可适用于多种模式通信设备中的模拟前端.
关键词:有源滤波器; 带宽可调; 增益可调; 高带外抑制; 低功耗
中图分类号: TN713 文献标志码: A DOI: 10.3969/j.issn.1000-5641.2022.02.017
Design of a reconfigurable active filter chip
YU Junwei, DIAO Shengxi
(School of Communication and Electronic Engineering, East China Normal University,
Shanghai 200241, China)
Abstract: Recently, research on multi-mode, multi-band transceivers has garnered significant interest; in this context, the Software-Define Radio (SDR) system is considered a good candidate. To reduce the negative influence of out-of-band interference on transceiver performance of the SDR system, a high out-of-band rejection IF (intermediate frequency) filter with tunable bandwidth and programable gain is proposed. The proposed filter consists of a biquadratic Gm-C filter, a gain- boosting stage, and a 5th-order elliptic filter. In the proposed filter, the variable gain is achieved using a biquadratic Gm-C filter and a gain-boosting stage, and the tunable bandwidth is achieved using capacitor arrays. In addition, a 5th-order elliptic filter is added to improve out-of-band rejection. The post-layout simulation shows that the bandwidth is tuned over a range of 1 MHz–30 MHz, and the minimum out-of-band rejection at twice the bandwidth reaches 44.56 dB. The gain control range is from –20 dB to 20 dB, and the power consumption and active area for the analog counterpart is 5.1 mW and 1.23 mm2 , respectively. The proposed filter is suitable for the analog front- end of multi-mode communication terminals.
Keywords: active filter; bandwidth tunable; gain programable; high out-of-band rejection; low power consumption
0 引言
隨着通信技术的高速发展 , 根据不同的通信需求 , 各式各样的通信协议被制定出.然而 , 这些通信协议却互不兼容 , 对采用不同协议的设备的相互通信造成了极大的不便.软件无线电技术正是为了解决这个难题而提出的.它是基于通用的硬件平台依靠软件配置不同的通信模式.其优点是允许1 个设备适用不同的通信系统 , 如蓝牙、 GPS、Wi-Fi (Wireless Fidelity)和 WLAN (Wireless Local Area Network)等交换数据 , 提高了设备的灵活性.软件无线电对模拟前端的设计提出了挑战 , 因为其需要具有大的动态范围和低功耗[1]. 在接收机中, 具有多模的中频低通滤波器是一个必不可少的模块.
因为通信協议的信道带宽不同且环境中存在较多的干扰信号 , 所以关于多模低通滤波器的研究大多集中在带宽调节范围和带外抑制上.文献[ 1- 2]提出的滤波器结构均具有较高的带外抑制, 但两者的功耗均较高;文献[ 3- 4]中提出的滤波器均具有较宽的带宽调节范围 , 前者具有带通、低通和高通这 3种输出模式 , 且功耗较低 , 后者具有低功率和高功率这2种模式 , 但两者的带外抑制均较小.而且文献[ 1- 4]中的滤波器均不具有增益调节功能 , 还需要搭配可变增益放大器才能对输出信号幅度进行控制.
本文系统地阐述了模拟前端中频低通滤波器的设计方法:首先 , 从应用出发 , 分析了无线通信对滤波器的带宽、带外抑制以及增益动态范围的需求;根据带外抑制的要求 , 在比较了同样的带外抑制需求下各种滤波器所需的阶数后 , 选择椭圆滤波器;根据增益动态范围的需求 , 对比了可变增益放大器和双二次 Gm-C滤波器的优缺点 , 选择双二次 Gm-C 滤波器;为了进一步提高增益范围 , 增加了一级增益提高级;带宽的调节方式是通过电容阵列对电路中使用的电容值进行放大和缩小来实现. 然后, 给出了双二次 Gm-C 滤波器、增益提高级和椭圆滤波器具体的电路实现. 仿真结果验证了本文提出的可变增益、可变带宽滤波器设计的可行性.
1 滤波器的要求
由于通信协议多种多样 , 不同的通信协议使用的信道带宽是有差别的 , 例如 , 蓝牙(IEEE802.15)的信道带宽为1 MHz;地面数字视频广播(Digital Video Broadcasting-Terrestrial, DVB-T)的信道带宽包括6 MHz、7 MHz 和8MHz; Wi-Fi (Wireless Fidelity, 802.11)的信道带宽为20 MHz;长期演进技术 (Long Term Evolution, LTE)的信号带宽包括1.4 MHz、3 MHz、5 MHz、10 MHz、15 MHz 和20 MHz.本文设计的滤波器的带宽调节范围为1 MHz ~30 MHz, 覆盖了Wi-Fi、蓝牙、地面数字视频广播和长期演进技术等通信协议定义的信道带宽范围.
随着 Wi-Fi 的普及以及数字蜂窝通信的演进 , 环境中的射频信号越来越复杂. 信号间的相互干扰会导致有用信号的信噪比降低 , 因此需要接收机具有很高的抑制带外干扰信号的能力. 在接收机中 , 中频域采用低通滤波器用于抑制带外干扰信号. 通常有用信号和干扰信号的频段较高 , 经过接收机的混频器下变频后 , 强干扰信号会距离有用信号较近 , 因此需要低通滤波器具有高带外抑制.滤波器的带外抑制要求可以从通信标准规定的干扰测试环境中得出 , 例如 , LTE 通信标准中 , 对于 Band21频段和10 MHz 信道带宽 , 有用信号电平为–91 dBm, 而在22.5 MHz 频率处的干扰信号为–56 dBm[5]. 为了使有用信号电平不低于干扰信号电平 , 低通滤波器在10 MHz 频率处的增益要大于在22.5 MHz 频率处的增益至少35 dB.
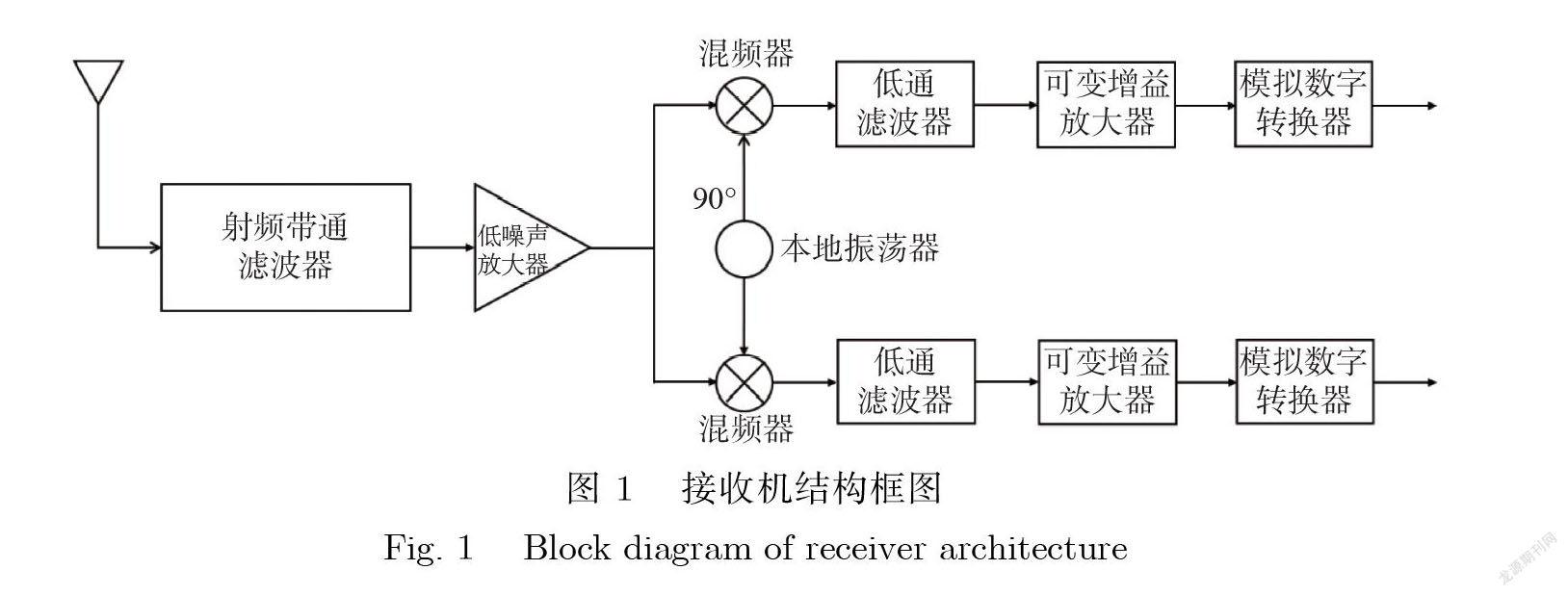
在同一个通信标准下 , 接收机在距离发射机不同位置接收到的信号幅度是不同的.在通信标准中 , 同样规定了有用信号的最大值和最小值 , 分别称为最大输入电平和参考灵敏度, 例如, 在 LTE 标准下, 对于 Band21频段和10 MHz 信道带宽 , 最大输入电平和参考灵敏度分别为–25 dBm 和–91 dBm.在接收机中 , 由于模数转换器的输入动态范围是固定的 , 因此需要接收机具有一定的增益动态范围来对接收到的信号幅度进行调节. 如图 1所示 , 在传统接收机中 , 往往将低通滤波器和可变增益放大器级联来抑制干扰信号和放大有用信号;如果模拟数字转换器的最大输入信号为0 dBm, 前几级电路的最小增益为45 dB, 则滤波器和增益可调放大器需要提供20 dB 的衰减. 所以, 可变增益放大器的增益范围为–20 dB ~20 dB 较为合适.本文设计了一个增益可调的低通滤波器来替代传统的级联方案, 从而减小接收机的面积.
因此 , 根据上述的性能需求 , 最后确定的指标是带宽的调节范围为1 MHz ~30 MHz, 其中在1 MHz ~10 MHz 范围内 , 步进为500 kHz;在 10 MHz ~20 MHz 范围内 , 步进1 MHz;在 20 MHz ~30 MHz 范围内 , 步进为2 MHz;在 2倍带宽频率处的带外抑制达到40 dB;增益范围为–20 dB ~20 dB, 步长为1 dB.
2 滤波器的架构
为了使滤波器带宽在10 MHz 时 , 能够在20 MHz 频率处达到40 dB 的带外抑制 , 巴特沃斯滤波器 (Butterworth filter)和切比雪夫Ⅰ型滤波器(Chebyshev Ⅰ filter)阶数分别至少为7 阶和6 阶 , 切比雪夫Ⅱ型滤波器(Chebyshev Ⅱ filter)和椭圆滤波器的阶数至少为5 阶[6]. 而椭圆滤波器使用的电感值总和小于切比雪夫Ⅱ型滤波器使用的电感值总和.而更小的感值 , 所需的面积也更小.同时 , 图 2表明椭圆滤波器的幅频曲线在截止频率(f)处更加陡峭 , 具有更窄的过渡带. 因此 , 本文选用椭圆滤波器来提高带外抑制.
然而仅使用椭圆滤波器无法实现对增益的调节 , 因此需要增加增益调节电路.这个电路的需求有:
①其增益可以调节 , 并且对整体滤波器的带宽影响小或无影响;②为了获得更高的带外抑制 , 其带宽需要与椭圆滤波器的截止频率接近 , 并且调节的范围要达到1 MHz ~30 MHz 的要求;③电路的功耗要小.虽然可变增益放大器可以实现可变增益 , 但是为了获得较大的带宽调节范围 , 往往需要消耗较大的功率[7]. 同时 , 在一个固定的带宽时 , 可变增益放大器的带宽通常比中频低通滤波器的带宽大得多 , 无法进一步提高带外抑制.基于上述考虑 , 本文中采用的增益调节电路为双二次 Gm-C 滤波器电路.它的增益调节可以通过调节电路中跨导运算放大器的跨导之比来实现. 并且 , 如果采用的跨导运算放大器没有内部节点 , 则不会有额外的寄生零极点影响整体的传输函数[8]. 因为跨导运算放大器工作时处于开环状态 , 其工作频率范围取决于单位增益带宽 , 所以能够达到很高的频率. Gm-C 滤波器还能够在低频下工作[9-10]. 因此, Gm-C 滤波器可以具有很宽的频率调节范围. 同时 , 双二次 Gm-C 滤波器还能够进一步提高整体滤波器的带外抑制.
如果只使用一级双二次 Gm-C 滤波器来实现增益调节 , 难以达到40 dB 的动态范围. 若双二次 Gm-C 滤波器的增益动态范围为20 dB, 则还需要增加一级增益提高级. 增益提高级的要求有:增益动态范围能够达到20 dB, 其–3 dB 带宽大于双二次滤波器和椭圆滤波器的带宽 , 使增益不会在滤波器的通带内下降.基于这些考虑 , 本文加入了一级增益提高级 , 它包括一个开环工作的跨导运算放大器和一个闭环工作的跨导运算放大器.
综上所述 , 本文提出的高带外抑制低通滤波器架构如图 3所示.它包括一级双二次滤波器、一级增益提高级和一级5 阶椭圆滤波器 , 其中 , 一级双二次滤波器和一级5 阶椭圆滤波器接收来自数字控制电路发送的带宽控制位(Bandwidth Control Bit, BWCB)并对带宽进行调节;双二次滤波器和增益提高级接收增益控制位(Gain Control Bit, GCB)并進行增益调节.
3 电路实现
3.1 跨导运算放大器设计
为了避免较大的功耗 , 本文使用了全差分共源级作为跨导运算放大器.跨导运算放大器和共模负反馈电路的原理图如图 4所示其中场效应管 M1– M6和电阻 R1组成全差分共源极电路由于输入晶体管工作在饱和区 , 则它们的跨导为
添加源极负反馈电阻 R1来获得线性跨导 , 则整体的跨导为
共模负反馈电路由场效应管 M7–M15组成. 共模负反馈电路的原理:当输出 Voutp 和 Voutn的共模电压提高时 , M7和 M8的源极即 M13和 M14的源极电压提高;然后 , M13和 M14的漏极电压提高 , M5、 M6、M15的栅极电压提高 , 使得输出 Voutp 和 Voutn的共模电压降低.
如图 5所示 , 电阻阵列用于实现可变跨导 , 这种方法的优点在于不会增加额外的功耗.对于第 i 位增益控制位 GGCB,i, 电阻R1 − Ri 1是与电阻 Ri串联的.这样可以提高电阻值 , 减小使用的电阻数 , 从而减小面积.
3.2 双二次 Gm-C 滤波器
双二次 Gm-C 滤波器结构如图 6所示, 其传输函数为[11]
其中 , ADC、!0和 Q 分别为直流增益、转折频率和品质因子. 从传输函数可以推导出:当 Q⩽√2/2时 , 幅频曲线单调递减;特别是当 Q =√2/2时 , 转折频率与–3 dB 带宽相等;当 Q >√2/2时 , 幅频曲线会在! =!0 处有1 个极大值为 Apeak = 2Q2ADC/ > ADC ;当 4Q2 −1 ≫0 时 , Apeak/ADC ≈ Q.
本文中, Gm3和 Gm4使用相同的跨导运算放大器, C1和 C2使用相同的电容阵列.在设计时 , 首先计算所需的转折频率 , 再根据公式(5)得出 Gm3与 C1的比值;然后根据所需的品质因子和公式(6)得出 Gm3与 Gm2的比值;最后 , 根据直流增益和公式(4)得到 Gm1与 Gm4的比值. 其中 , Gm1的跨导通过上述的电阻阵列实现可调 , Gm2– Gm4的跨导固定. 频率的调节通过电容阵列实现 , 如图 7所示. 对于第 i 位带宽控制位 BBWCB,i, 电容 C1– Ci–1 与电容 Ci并联. 这样可以提高电容值 , 减小使用的电容数 , 进一步减小面积.
3.3 增益提高级
如果仅使用一级双二次 Gm-C 滤波器调节增益, 并且考虑椭圆滤波器的插入损耗, 则 Gm1的最大值和最小值需要达到约19.95× Gm4和 0.1995 × Gm4.这对 Gm1提出了严格的要求.在本文中 , 提出了两种方案来减小 Gm1的设计难度.第一种方案是对 Gm1进行并联 , 如图 8所示.由图 8可知 , 当开关打开和关闭时 , 增益分别等于4 ×(Gm1/Gm4)和 Gm1/Gm4.这种方案可以提高12 dB 的增益动态范围.
第二种方案是增加一级增益提高级 , 其结构如图 9所示 , 其中 Gm6在低频下可以等效为1 个阻值为 1/Gm6的电阻. 对于理想模型 , 其增益为
相似地 , 将多个 Gm5进行并联来提高增益动态范围. 然而 , Gm5具有有限的输出阻抗. 因此对增益提高级重新建模 , 实际模型如图 10所示 , 其中 Ro5和 RL 分别为 Gm5和 Gm6的低频输出电阻和低频等效电阻 , 则当开关处于关闭和打开时 , 增益分别为
其中, N 为 Gm5的并联个数 , 则增益的变化为
当 Gm6固定时 , RL 固定.从公式(10)中可以得到, 当 N 趋于无穷大时 , 最大增益变化能达到20log10(1+ Ro5/RL). Gm5同样使用电阻阵列来实现可变跨导.
3.4 5阶椭圆滤波器
图 11是全差分5 阶椭圆滤波器的无源形式, 其中的无源电感需用跨导运算放大器和电容替代.如图 12所示, 利用2 个跨导运算放大器和1 个电容形成接地电感 , 由原理图可得
整理公式(11)–公式(13)可以得到输入端的等效阻抗
则等效的电感值为
对于浮地电感则需要使用4个跨导运算放大器和1 个电容实现. 全差分5 阶椭圆滤波器的有源
形式如图 13所示.根据电感公式(15)可知电容值和跨导值的平方成正比关系.如果电容值过小 , 则带宽受到寄生电容的影响就会很大 , 如果电容值过大 , 则会导致需要的跨导值较大 , 这意味着较大的功耗和较大的面积. 因此, 选取电容值的大小需要在带宽、功耗和面积之间折中.
4仿真结果
提出的可调带宽可调增益高带外抑制低通滤波器使用65 nm CMOS 工艺实现 , 版图如图 14所示. 图 14中, 模拟部分的核心面积为1.23mm2 , 使用了1.3 V 和2.5 V 的电源电压, 模拟部分的总功耗为5.1 mW.
图 15所示是带宽为10 MHz、增益为20 dB 时滤波器幅频曲线的前仿真和后仿真结果对比.对比图1 5中的前仿真和后仿真结果可知 , 增益从23.2 dB 降低到了20.0 dB, 带宽从11.16 MHz 降低到了10.03 MHz, 2倍带宽频率的带外抑制从48.1 dB 提高到了49.6 dB.增益的降低主要是因为寄生电阻降低了跨导放大器的等效跨导 , 导致跨导比降低.带宽的降低主要是因为金属层走线产生了寄生电容.同时寄生效应也使2 倍带宽频率的带外抑制产生了一定的变化 , 但仍满足2倍频带外抑制的指标. 同时 , 后仿真结果显示 , 在22.5 MHz 时 , 滤波器的带外抑制约为47.73 dB, 可以满足 LTE通信标准中 , Band 21频段和10 MHz 的信道带宽下的带外抑制要求. 图16是增益为20 dB 时 , 濾波器在不同带宽情况下的后仿真结果. 从图 16中可以得知 , 在1 MHz ~30 MHz 具有34种带宽 , 部分结果如表 1所示.由表1可知, 当带宽为30.21 MHz 时, 2倍带宽频率的带外抑制最大值为68.90 dB;当带宽为1.03 MHz 时 , 2倍带宽频率的带外抑制最小值为44.56 dB;而在其他带宽下 , 具有一定的波动 , 但始终都在指标范围内.
当带宽为10 MHz 时 , 滤波器在不同增益情况下的幅频曲线后仿真结果如图 17.从图1 7中可知 , 增益的范围为–20 dB ~20 dB, 部分结果如表 2所示.由表2可知, 当增益减小时 , 带宽从10.03 MHz略微提高到10.10 MHz, 2倍带宽频率的带外抑制从49.59 dB 减小到46.81 dB. 表 3是本文提出的滤波器与部分文献滤波器的比较. 从表 3中可以得出 , 本文提出的滤波器具有调节增益的功能 , 这是文献 [1-4]和文献[9]提出的滤波器所不具备的;同时本文提出的滤波器还具有较高的带外抑制 , 功耗也较低.
5 结论
本文针对软件无线电的模拟前端提出了一个可调增益、可调带宽的高带外抑制中频滤波器.该滤波器采用全差分共源级作为跨导运算放大器 , 通过数字控制改变源极负反馈电阻的阻值 , 实现了可变跨导 , 避免了额外的功耗.滤波器由双二次 Gm-C 滤波器 , 增益提高级和5 阶椭圆滤波器级联组成.使用的五阶椭圆滤波器提高带外抑制能力. 同时 , 双二次 Gm-C 滤波器不仅可以进一步提高带外抑制 , 还能通过调节跨导比实现可变增益.增益提高级则是进一步提高了增益动态范围. 由于带宽和增益均可调 , 该滤波器可以取代传统的低通滤波器和可变增益放大器级联的结构 , 可以减小接收机整体的面积 , 适合应用于多模通信设备的模拟前端中.
[参考文献]
[1] LEWINSKI A J, SILVA-MARTINEZ J. A 30-MHz fifth-order elliptic low-pass CMOS filter with 65-dB spurious-free dynamic range[J]. IEEE Transactions on Circuit and Systems I: Regular Papers, 2007, 54(3):469-480.
[2] LAXMINIDHI T, PRASADU V, PAVAN S. Widely programmable high-frequency active RC filters in CMOS technology [J]. IEEETransactions on Circuit and Systems I: Regular Papers, 2009, 56(2):469-480.
[3] BEG P, MAHESHWARI S, SIDDIQI M A. Digitally controlled fully differential voltage- and transadmittance-mode biquadratic filter[J]. IET Circuits, Devices & Systems, 2013, 7(4):193-203.
[4]东尚清.可调带宽低功耗超宽带Gm-C低通滤波器的研究与设计[D].上海:复旦大学, 2013.
[5]张欣旺.面向行业专网的软件无线电接收机芯片关键技术研究[D].北京:清华大学, 2015.
[6] SCHAUMANN R, VALKENBURG M E V. Design of Analog Filters [M]. New York: Oxford University Press, 2001.
[7] RAY S, HELLA M M. A 10 Gb/s inductorless AGC amplifier With 40 dB linear variable gain control in 0.13µm CMOS [J]. IEEEJournal of Solid-State Circuit, 2016, 51(2):440-456.
[8] NAUTA B. A CMOS Transconductance-C filter technique for very high frequencies [J]. IEEE Journal of Solid-State Circuit, 1992,27(2):142-153.
[9] REZAEI F. Adaptive gm3 cancellation linearisation and its application to wide-tunable Gm-C filter design [J]. IET Circuits, Devices &Systems, 2017, 11(5):478-486.
[10] CROMBEZ P, CRANINCKX J, STEYAERT M. A 100kHz-20MHz reconfigurable nauta Gm-C biquad low-pass filter in 0.13µmCMOS [C]// IEEE Asian Solid-State Circuits Conference. IEEE, 2007:444-447.
[11] CROMBEZ P, CRANINCKX J, STEYAERT M. A linearity and power efficient design strategy for architecture optimization of Gm-Cbiquadratic filters [C]//2007 Ph. D Research in Microelectronics and Electronics Conference. IEEE, 2007:229-232. DOI:10.1109/RME.2007.4401854.
(责任编辑:李艺)
