双色光绝热冷却原子数值优化的研究

钱晨扬 董光炯

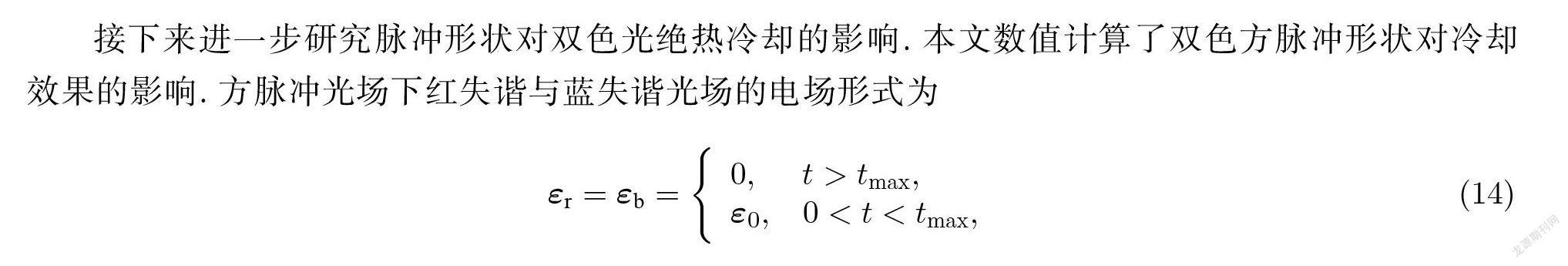
摘要： 双色光绝热冷却原子方法是近年来发展出的一种不需要依靠自发辐射的激光冷却方法 ， 然而效率不高.通过数值模拟方法优化了双色光绝热冷却的过程 ， 发现存在最佳的双色光场脉冲时间从而获得最佳冷却效果;比较了使用高斯光脉冲和方脉冲这两种脉冲的冷却效果 ， 发现脉冲形式对冷却效果无显著影响. 由于该数值模拟方法依赖于光场-原子系统的绝热演化 ， 数值研究表明 ， 降低原子束的速度能够提高冷却效果.最后研究了自发辐射对双色光绝热的影响 ， 发现在脉冲时间较长时自发辐射会降低冷却效果.

关键词：双色光绝热冷却;  冷原子;  光力

中图分类号： O439    文献标志码： A    DOI：  10.3969/j.issn.1000-5641.2022.02.015

Numerical optimization of bichromatic adiabatic cooling

QIAN Chenyang，  DONG Guangjiong

（State Key Laboratory of Precision Spectroscopy， East China Normal University， Shanghai  200214， China）

Abstract： In recent years， a new laser cooling method—named bichromatic adiabatic cooling—has been developed; however， the method offers low cooling efficiency. In this paper， numerical optimization of the bichromatic adiabatic cooling process has been performed. It is shown that there is an optimal pulse time for the optical fields to achieve the highest cooling efficiency. Moreover， a comparison of the cooling efficiency with the Gaussian light pulse and square pulse shows that the cooling efficiency is insensitive to the pulse shape. Because this cooling method relies on adiabatic evolution of the light field-atom system， it is shown that it is better to slow the speed of the atomic beam to maintain the adiabatic condition. Finally， the effect of spontaneous emission on bichromatic adiabatic cooling is studied. The results show that use of a long pulse significantly reduces cooling efficiency.

Keywords： bichromatic adiabatic cooling;  cold atom;  optical force

0  引言

利用激光光场降低原子分子气体温度的激光冷却技術能够把碱金属原子气体等降低到微开甚至纳开的量级[1-2] ， 这为实现玻色-爱因斯坦凝聚[3]与费米子简并系统[3]开辟了道路 ， 并由此发展出了基于物质波光学的精密测量技术[4]以及量子仿真平台[4]. 然而 ， 除少数原子之外 ， 元素周期表上的大部分原子都无法被激光冷却[5].为解决该问题 ， 文献[6]提出了双色光绝热冷却技术. 该技术利用原子气体与双色光场体系的绝热能级交叉处的朗道塞纳隧穿效应[7] ， 把原子气体的动能转移到双色光场 ， 从而在脉冲光场关闭后显现原子气体的冷却现象[7]. 该原理已被实验证实[7] ， 这种冷却技术不依赖闭合的能级循环 ， 具有一定的普适性;然而它的冷却效率比现有的其他冷却方法[5]的效率低 ， 需要在理论上进一步探索其理论机制并优化提高冷却效果.为此， 本论文通过数值模拟的方式来优化双色光绝热冷却过程， 并探究光脉冲长度、原子气体中心速度与自发辐射对于双色光绝热冷却效率的影响.

本文后续结构：第1章介绍双色光绝热冷却的理论模型和所使用的数值计算方法;第2章开展双色光绝热冷却的优化研究;第3章总结全文.

1  双色光绝热冷却的理论模型

本文双色光绝热冷却的理论模型如图  1所示： 1个共振频率为！a 的二能级原子受到频率为！b 和！r 的2个光学驻波的作用 ， 驻波由1组相反传播的光束相互干涉形成.把向右传播的光场的波矢量记为 kb 与 kr ， 光的电场记为"b 与"r .这两束光分别是蓝失谐光和红失谐光 ， 它们的频率分别表示为， 其中为失谐量.

原子气体中单个原子的哈密顿量由原子的自由哈密顿量Hˆ0（r） （r 为以原子为中心的坐标）和双色光场与原子相互作用的哈密顿量HˆAL 构成 ， 即

其中

其中， Z 为实验室地面坐标  r ;  b 是相位， dˆ（r）是电偶极子算符.

在以原子基态和激发态构成的希尔伯特空间中 ， 哈密顿量的矩阵表示为

其中

且

其中， |e（r）⟩为能收原子的激发态 ， |g（r）⟩为能收原子的基态.

把原子的密度矩阵记为ˆ ， 它满足的海森堡运动方程为

其中， 衰减系数的矩阵将矩阵形式的哈密顿量式（3）代入运动方程（5）得到

其中

在模拟中， 根据文献[ 7]的实验 ， 本文使用高斯光脉冲进行模拟. 红失谐与蓝失谐光场的电场形式为

其中 ， t 为时间 ， th为光场强度达到最大值的时间 ，  为高斯脉冲的 e–1 宽度 ， "0为高斯光脉冲峰值处的电场强度. 单个原子在光场中受到的外力为 F（Z）= −Tr[ˆ∇ZHˆAL];利用公式（4）可得

进一步根据牛顿第二定律 ， 这个原子的速度v（t）满足运动方程

利用公式（6）和公式（11）来研究冷却过程 ， 对原子气体内每个原子的运动状态作数值计算.具体的数值计算过程如下.

构造 1个由大量原子组成的原子气体 .每个原子在初始情况下各个密度矩阵元的值为 gg （0）= 1; ee （0）=  ge （0）=  eg （0）= 0.

在数值模拟中 ， 取1 个很小的时间间隔∆T ， 令Tn+1 =（n +1）∆T ， 通过运动方程公式（11）可以近似得到Tn+1时刻的原子速度的近似计算公式 ， 具体为

通过速度公式（12）计算出Tn+1时刻的原子位置

接下来利用Tn时刻该原子的密度矩阵 ， 通过龙格库塔法[8]求解方程组（6） ， 得到该原子在Tn+1时刻的密度矩阵ˆ（Tn+1）. 通过数值演化的方式 ， 由Tn时刻的原子速度、位置和密度矩阵得到Tn+1时刻的原子速度、位置和密度矩阵. 通过该方法对原子的初始速度进行数值演化 ， 能够得到该原子速度的时间演化过程.最后对原子气体中的每一个原子都做上述数值演化 ， 得到原子气体中每个原子的速度随时间的演化 ， 并以此获得原子气体内原子的速度分布随时间的演化.

在文献[  7]中 ， 光场参数Ω0被定义为Ω0 = d（r）· "0/ℏ. 在原子气体的电偶极矩確定的情况下 ， 该参数能够反映冷却光场电场强度的大小. 根据文献[  7]对光场参数Ω0的优化结果 ， 在数值模拟中 ， 本文将光场的电场强度以及空间相位设定为与双色光场冷却 He 原子气体的实验一致[7] ， 令光场参数Ω0和公式（7）中的变量、为Ω0 =36 MHz; =π/4;  =25 MHz：

2  双色光绝热冷却原子的数值研究

本文针对文献[  7]所使用的 He 原子开展了绝热冷却的数值优化研究. 在模拟中 ， 选用40万个二能级 He 原子 ， 所使用的二能级为原子的23S 与33P 能级 ， 能级之间的跃迁波长为389 nm.原子气体的初始速度分布为在–15 m/s 至15 m/s 范围内的均匀分布.原子气体的初始位置分布为一个空间宽度为 500µm 的均匀分布.数值模拟的双色光场为失谐量=25 MHz， Ω0 =36 MHz ， He 原子的自发辐射率为  =3：85× 106/s .

2.1  双色光场冷却 He 原子气体的数值模拟结果与实验冷却结果的比较

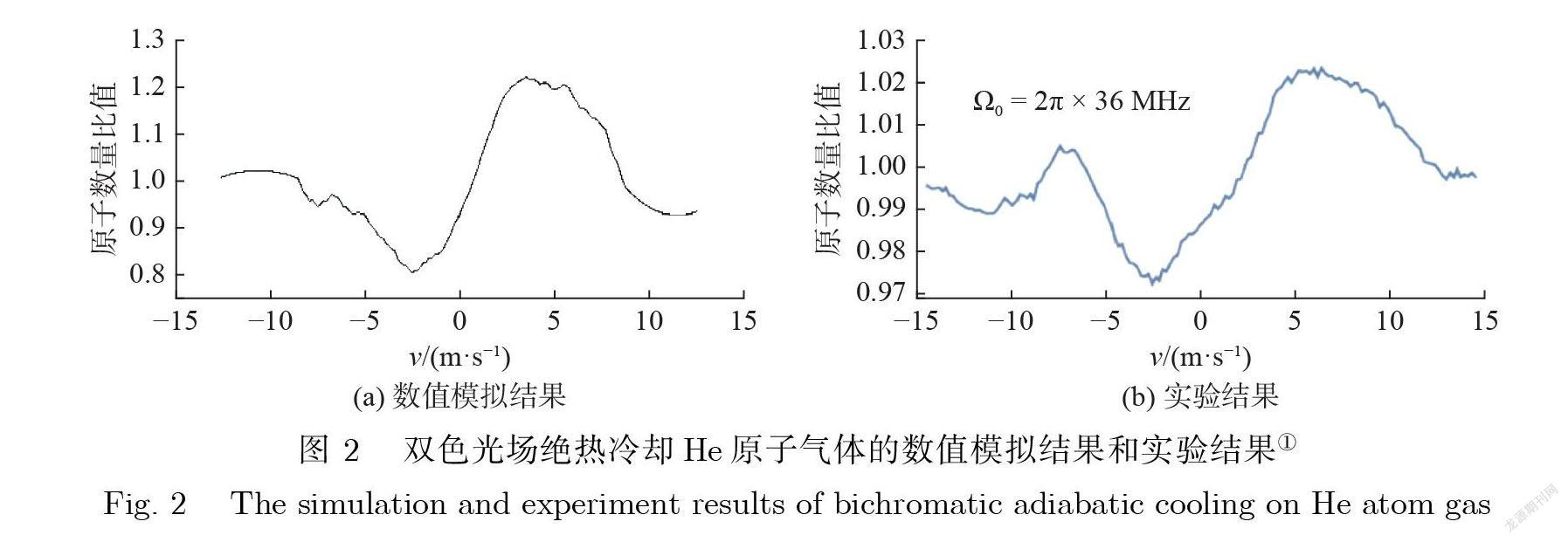
本文先模拟了文献[  7]的实验结果. 文献[  7]实验中使用的光脉冲其电场形式见公式（9）.在模拟中， 根据文献[  7]中的 =380 ns （ 为高斯脉冲的 e  1宽度）， 将该光场电场形式（公式（9））代入公式（2）的哈密顿量 ， 并通过第1 章中公式（1）–公式（13）的数值模拟方法 ， 计算出双色光冷却完成后的 He 原子气体速度分布. 将–13 m/s 至13 m/s 的速度区间平均分为800个小的速度区间 ， 设定每个速度区间的宽度为0.0325 m/s， 计算每个速度区间内 He 原子在受到光场作用之后和作用之前数量的比值. 该原子数量比值可以反映原子在某些特定速度区域内的聚集情况 ， 比值越大 ， 说明聚集情况越明显 ， 冷却效果越好.

图   2（a）为考虑自发辐射对双色光场冷却 He 原子气体的实验进行数值模拟的结果：原子气体速度（v）分布出现了在速度4 m/s 附近区域聚集的现象 ， 在聚集处 ， 原子数量与冷却前的原子数量比值为1.21.    图   2（b）为双色光冷却 He 原子气体实验中所得到的结果：原子气体速度分布出现了在速度5 m/s 附近区域聚集的现象 ， 在聚集处 ， 原子数量与冷却前的原子数量比值为1.02.

从图   2（a）与图   2（b）的结果来看 ， 虽然聚集的程度不同 ， 但原子气体速度分布都出现了往4 m/s 至5 m/s 附近区域聚集的情况 ， 数值模拟的结果与实验结果相似.

2.2  双色光作用时长与双色光场脉冲形状对于冷却效果的影响

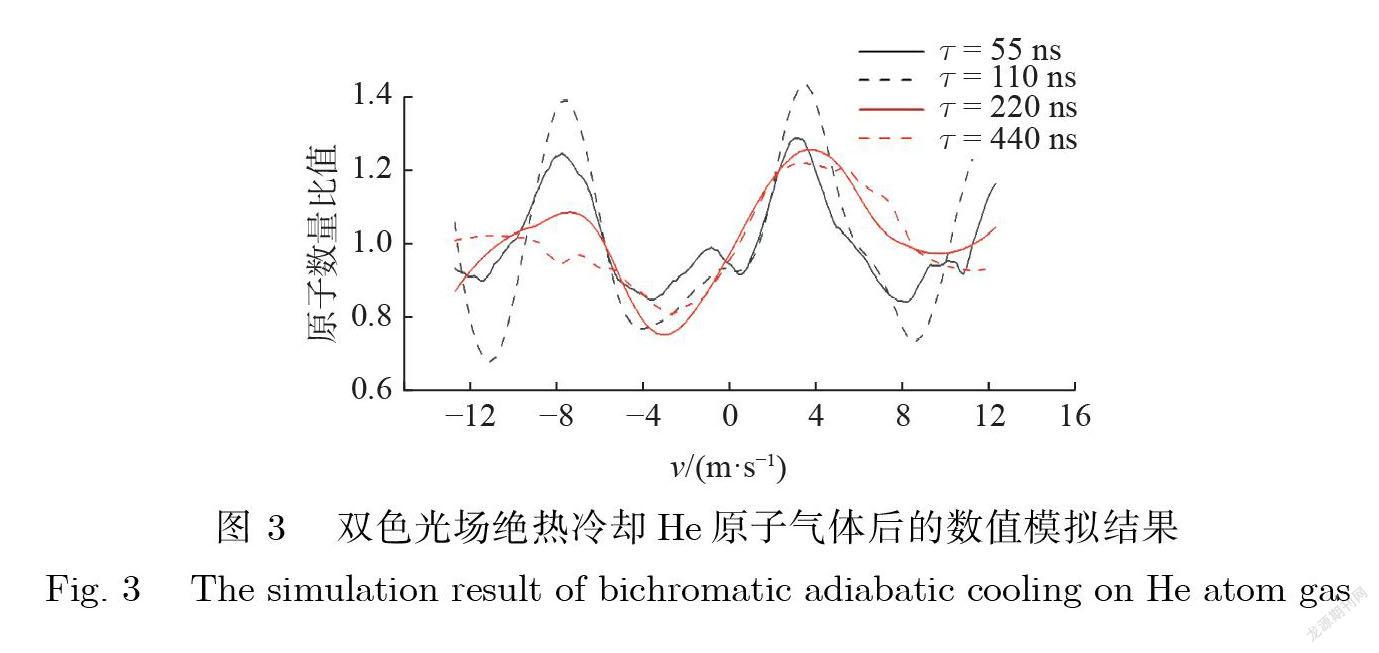
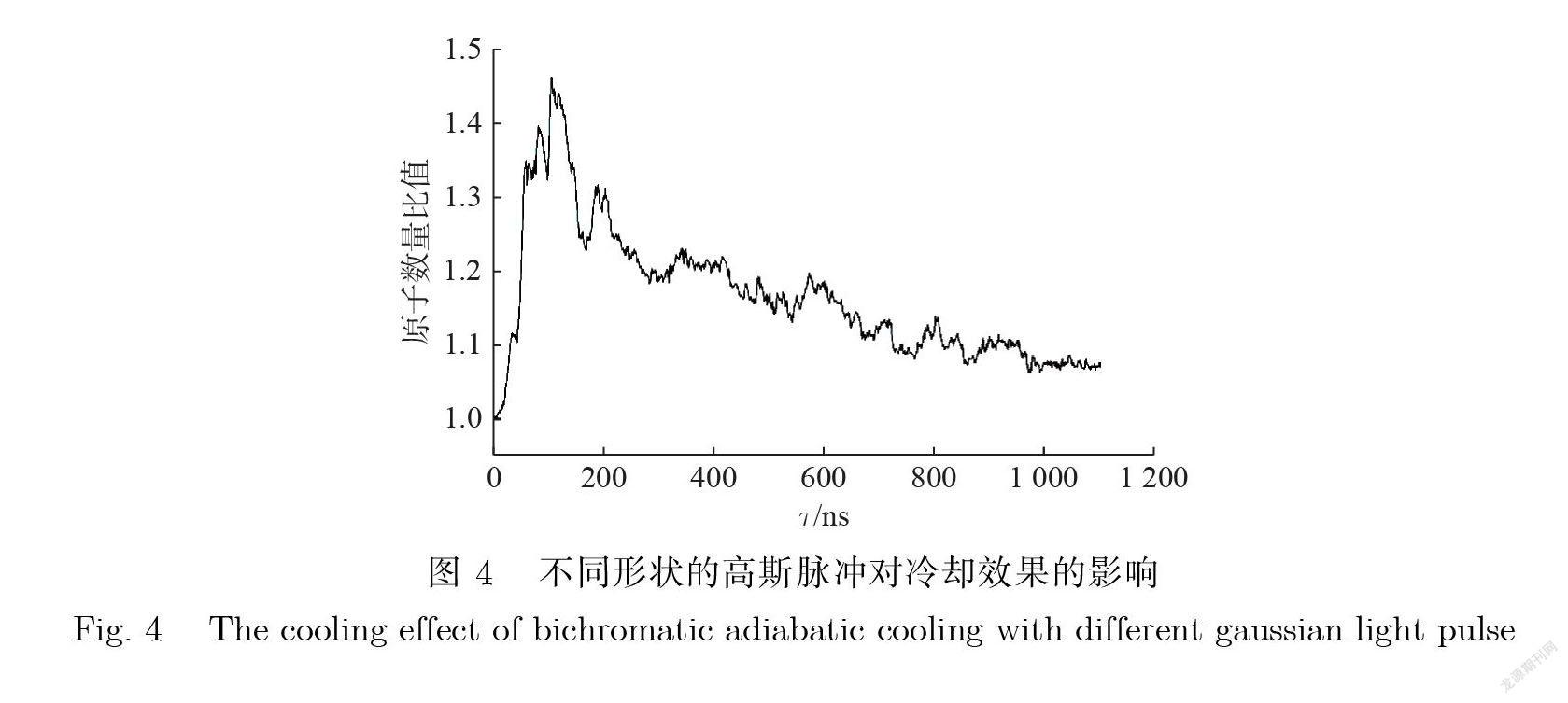
本文首先研究光场脉冲长度与脉冲形状对双色光绝热冷却的影响. 双色光场的失谐量依旧为 =25 MHz， Ω0 =36 MHz .改变高斯脉冲的 e–1 宽度来比较不同作用时间对冷却效果的影响.   图  3为不同高斯脉冲的 e–1 宽度（ ） 下数值模拟的结果.   图  3中的4 条线分别为 =55 ns， 110 ns， 220 ns， 440 ns 的双色光场高斯脉冲作用于 He 原子气体后的数值模拟结果.当 = 55 ns 时 ， 原子气体速度分布出现了在速度–7.6 m/s 和3.4 m/s 附近区域聚集的现象 ， 在聚集处 ， 原子数量与冷却前的原子数量比值分别为1.23和 1.27;当 = 110 ns 时， 原子气体速度分布出现了在速度–7.5 m/s、3.6 m/s 和11.8 m/s 附近区域聚集的现象 ， 在聚集处 ， 原子数量与冷却前的原子数量比值分别为1.39、1.40和 1.25;当 = 220 ns 时 ， 原子气体速度分布出现了在速度–7.5 m/s 和3.7 m/s 附近区域聚集的现象 ， 在聚集处 ， 原子数量与冷却前的原子数量比值分别为1.08和 1.25;当 = 440 ns 时 ， 原子气体速度分布出现了在速度 4 m/s 附近区域聚集的现象 ， 在聚集处 ， 原子数量与冷却前的原子数量比值为1.21.由于图3 中各图的 v 分布都在3.8 m/s 附近的区域有聚集现象 ， 因此 ， 可通过比较各个作用时间下该区域的聚集现象来判断双色光场对原子气体的冷却效果.通过比较各个模拟结果 ， 本文发现 ， 高斯脉冲的 e–1 宽度不同 ， 原子气体在 v =3.8 m/s 附近的区域的聚集程度不同.  图  4为不同 e–1 宽度的高斯脉冲双色光作用在 He 原子气体上后 ， 原子气体在 v =3.8 m/s 附近区域聚集处的原子数量与冷却前的原子数量比值 ， 该比值在 =104 ns 时达到最大值1.46.这说明 ， 当使用 =103 ns 的双色光高斯脉冲冷却 He 原子气体时 ， 双色光绝热冷却的效果最好.通过该模拟的方法 ， 能找到最佳的高斯脉冲的 e–1 宽度 ， 使得原子在该区间的聚集程度最大、双色光绝热冷却的效果最佳.这说明本文的数值模拟方法可以帮助寻找最佳的作用时间 ，

接下来进一步研究脉冲形状对双色光绝热冷却的影响. 本文数值计算了双色方脉冲形状对冷却效果的影响. 方脉冲光场下红失谐与蓝失谐光场的电场形式为

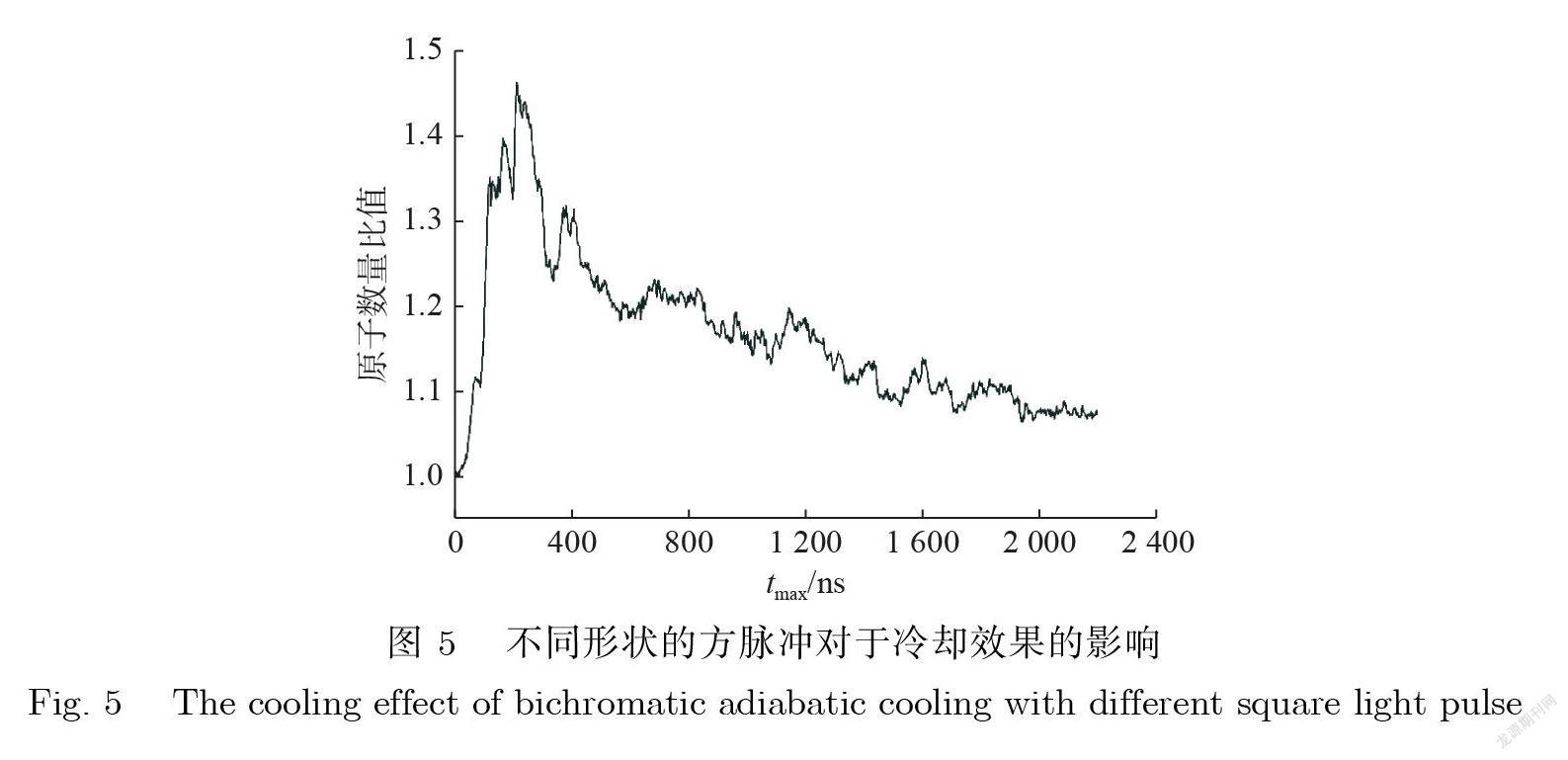
其中 ， tmax为方脉冲宽度. 利用公式（14）替换数值模拟中的公式（9）， 再进行数值模拟 ， 能够得到方脉冲作用下原子气体被冷却的结果.   图  5为不同宽度的方脉冲双色光场作用在 He 原子气体上后 ， 原子气体在速度3.8 m/s 附近区域聚集的原子数量与冷却前的原子数量比值. 在方脉冲宽度为209时 ， 该比值达到最大为1.46.与高斯脉冲相比（  图  4）没有区别 ， 因此这个绝热方法对脉冲形状不敏感.

2.3  原子气体中心速度对于冷却效果的影响

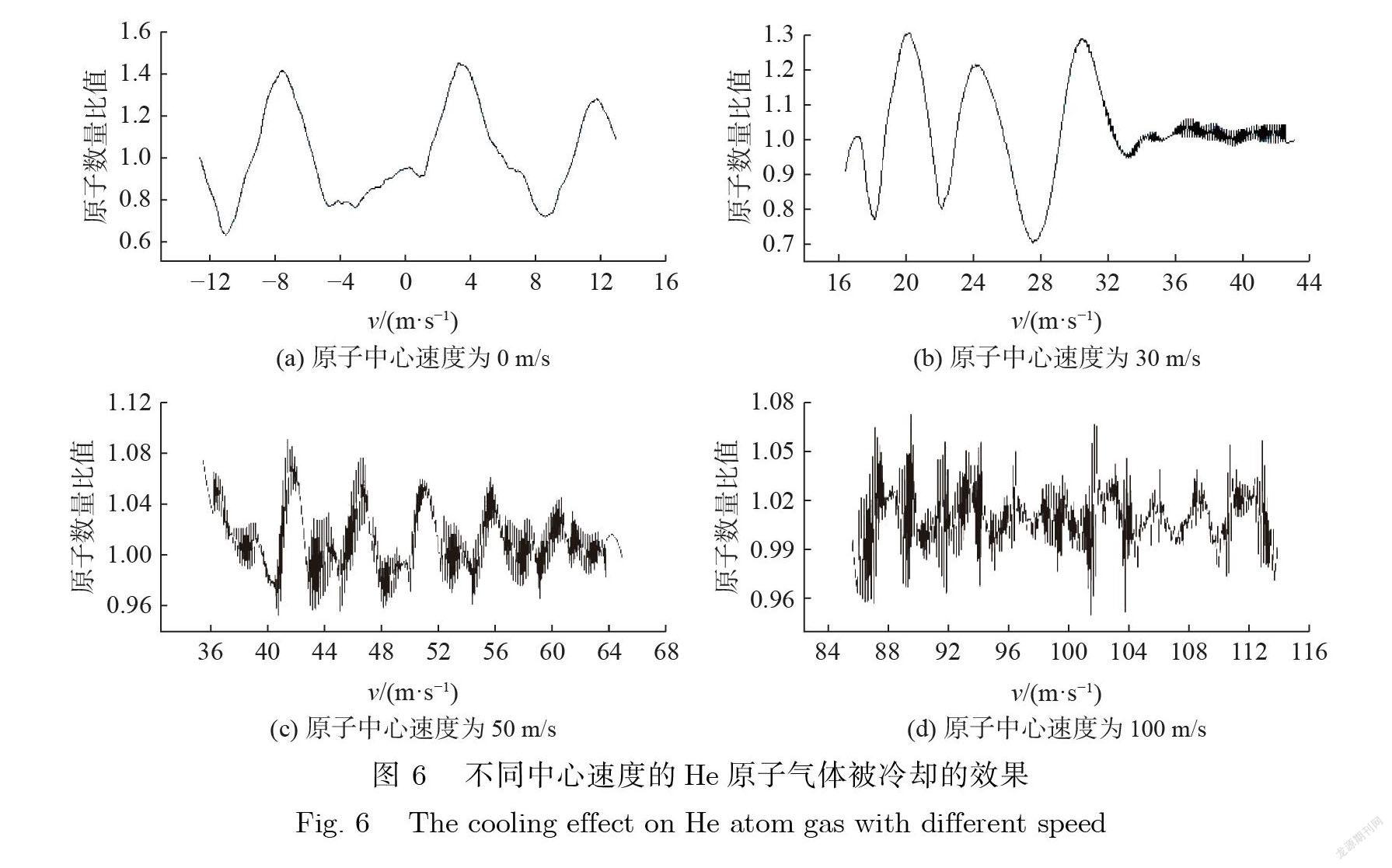
原子气体的中心速度会影响冷却效果.  图  6表示的是不同中心速度的原子气体被 =110 ns 的高斯脉冲冷却的结果.   图  6（a）的原子气体的中心速度为0 m/s， 原子气体速度（v）分布出现了在速度  –7.5 m/s、3.6 m/s、11.8 m/s 附近区域聚集的现象 ， 在聚集处 ， 原子数量与冷却前的原子数量比值分别为1.39、1.40、1.27.  图  6（b）的原子气体中心速度为30 m/s， 原子气体速度分布出现了在速度–20.2 m/s、24.3 m/s、30.4 m/s 附近区域聚集的现象 ， 在聚集处 ， 原子数量与冷却前的原子数量比值分别为1.29、1.2、1.27.  图  6（c）和图  6（d）中 ， 原子气体的中心速度分别为50 m/s 和100 m/s， 在这2 幅图中观察不到原子聚集的现象. 比较图  6（a）至图  6（d）这 4幅图 ， 可以发现 ， 随着原子中心速度的增加 ， 原子向某一速度附近区域聚集的现象不断减弱 ， 说明双色光绝热冷却适用于气体内原子中心速度较低的原子气体.这是因为这个冷却方法要求原子光场相互作用系统绝热演化 ， 当原子气体速度太快时 ， 该过程将变为一个非绝热过程从而使得冷却无法正常进行 ， 因此在冷却前需要降低原子束速度.

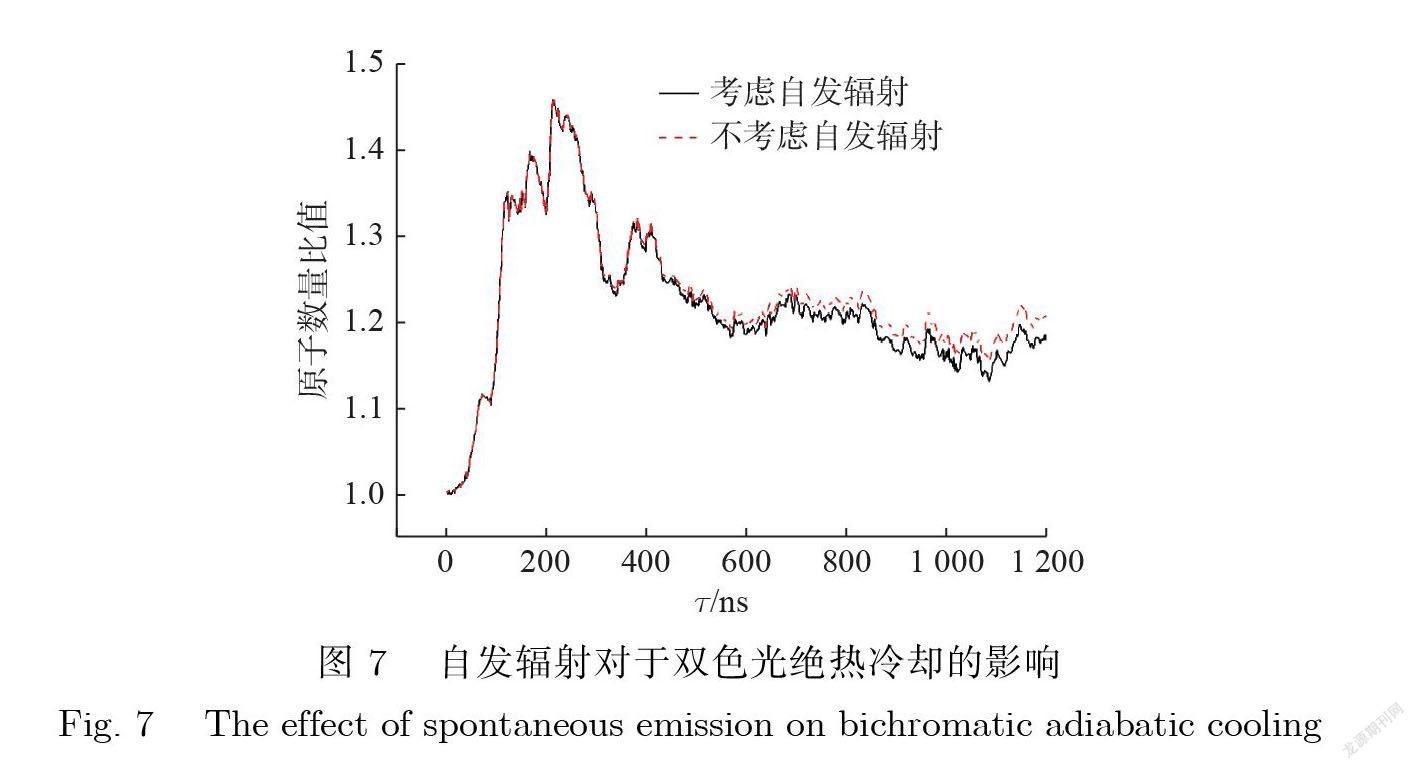
2.4  自发辐射对双色光绝热冷却效果的影响

文献[ 7]认为 ， 当双色光场的作用时间较长时 ， 原子的自发辐射会降低双色光绝热冷却的效果.本节在数值模拟时不考虑自发辐射研究自发辐射对双色光绝热冷却的影响.   图  7为不同高斯脉冲 e–1 宽度（ ）的双色光场作用在 He 原子气体上后 ， 原子气体在原子气体速度 v =3.8 m/s 附近区域聚集的原子数量与冷却前的原子数量比值 ， 其中 ， 实线为考虑自发辐射的数值模拟结果 ， 虚线为不考虑自发辐射的数值模拟结果.从图  7看出 ， 当光场的作用时间较短时 ， 由于原子的自发辐射次数较少 ， 自发辐射对于冷却效果的影响不明显;当光场的作用时间变长时 ， 自发辐射显著降低冷却效果.本文认为产生这种现象的原因类似于多普勒冷却极限产生的原因：由于自发辐射出的光子方向不可控使得被双色光场聚集在某一速度区域附近的原子被随机加速或者减速 ， 造成了聚集效果的下降.

3  总结

本文研究了双色高斯光脉冲时间长度对绝热冷却效果的影响 ， 发现存在一個最佳的双色光场作用时间使得双色光绝热冷却的效果最佳;比较了双色高斯光脉冲和双色方光脉冲对绝热冷却的影响 ， 发现在冷却效率上没有显著差异. 此外 ， 由于双色光绝热冷却过程需要原子气体与双色光场体系的绝热演化 ， 本文模拟发现 ， 双色光绝热冷却的方法更适合冷却中心速度较低的原子气体 ， 因此原子束需要减速.在双色光场作用时间较长时 ， 自发辐射显著降低冷却效果.这是由于自发辐射出的光子方向不可控， 使得被双色光场聚集在某一速度区域附近的原子被随机加速或者减速 ， 造成了聚集效果下降.

[参考文献]

[1] CHU S， HOLLBERG L， BJORKHOLM J E， et al. Three-dimensional viscous confinement and cooling of atoms by resonance radiationpressure [J]. Physical Review Letters， 1985， 55（1）：48-51.

[2]ASPET A， ARIMONDO E， KAISER R， et al. Laser cooling below the one-photon recoil energy by velocity-selective coherent population trapping[J]， Physical Review Letters， 1988， 61（7）：826-829.

[3]ANDERSON M H， ENSHER J R， MATHEWS M R， et al. Observation of Bose-Einstein condensation in a dilute atomic vapor [G]// Collected Papers of Carl Wieman.[S. l.]： World Scientific Publishing Co Pte Ltd， 2008：453-456.

[4]ZHANG W Z， LIU W M. QED-based optical bloch equations without electric dipole-approximation： A model for a two-level atom interacting with a monochromatic X-ray laser beam [EB/OL].（2012-09-04）[2021-03-01]. https：//arxiv.org/abs/1206.3445.

[5]LAwALL J， BARDOU F， SAUBAEM B， et al. Two-dimensional subrecoil laser cooling [J]. Physical Review Letters， 1994， 73（14）：1915-1918.

[6]SÖDING J， GRIMM R， OVCHINNIKOV Y B， et al. Short-distance atomic beam deceleration with a stimulated light force [J]. Physical Review Letters， 1997， 78（8）：1420-1423.

[7]CORDER C， ARNOLD B， HUA X， et al. Laser cooling without spontaneous emission using the bichromatic force [J]. Journal of the Optical Society of America B， 2015， 32（5）： B75-B83.

[8]李庆扬.数值分析[M].北京：清华大学出版社有限公司， 2001.

（责任编辑：李艺）