PT对称势下自旋轨道耦合玻色-爱因斯坦凝聚体的能带结构
2024-05-15邵凯花马金萍王青青席保龙石玉仁
邵凯花 马金萍 王青青 席保龙 石玉仁


DOI:10.16783/j.cnki.nwnuz.2024.03.005
收稿日期:2023-12-10;修改稿收到日期:2024-02-05
基金项目:国家自然科学基金资助项目(12065022)
作者简介:邵凯花(1997—),女,甘肃天水人,硕士研究生.主要研究方向为非线性物理.
E-mail:2859854460@qq.com
*通信联系人,男,教授,博士,博士研究生导师.主要研究方向为非线性物理.
E-mail:shiyr@nwnu.edu.cn
摘要:数值研究PT对称势下具有自旋轨道耦合玻色-爱因斯坦凝聚体的能带结构.用傅立叶配置法求解布洛赫能带,分析PT对称晶格势的深度、虚部相对大小、自旋轨道耦合强度和拉比耦合强度对能带结构的影响.结果表明,第一、二能带的上下边沿随晶格深度的增加而上升,但能带宽度变窄;当PT对称晶格势的虚部大于临界值时,第一和第二能带发生重叠;随着自旋轨道耦合强度的增大,第一和第二能带的上下边界均减小;拉比耦合强度对能带结构也具有重要影响.
关键词:玻色-爱因斯坦凝聚;PT对称势;自旋轨道耦合;能带结构
中图分类号:O 145 文献标志码:A 文章编号:1001-988Ⅹ(2024)03-0042-06
Band structures in spin-orbit coupled Bose-Einstein
condensate with PT symmetric potential
SHAO Kai-hua,MA Jin-ping,WANG Qing-qing,XI Bao-Long,SHI Yu-ren
(College of Physics and Electronic Engineering,Northwest Normal University,Lanzhou 730070,Gansu,China)
Abstract:The band structures in spin-orbit coupled Bose-Einstein condensate with PT symmetric potential are investigated numerically.The Bloch bands are obtained by the Fourier collocation method and the effects of the depth of PT symmetric lattice potential,the magnitude of imaginary part,the spin-orbit coupled strength and the Rabi coupling strength on band structures are analyzed.The results indicate that the upper and lower boundaries of the first and second bands increase with the increase of lattice depth,but the width of band becomes narrower.The first and second bands overlap when the imaginary part of the PT symmetric lattice potential is larger than the critical value.For the first and second bands,their upper and lower boundaries decrease with the increase of spin-orbit coupled strength.It is also found that the Rabbi coupling strength also has an important effect on the band structure.
Key words:Bose-Einstein condensate;PT symmetric potential;spin-orbit coupling;band structure
玻色-爱因斯坦凝聚(Bose-Einstein conden- sate, BEC)是指系统的温度低于临界温度时,所有原子都聚集在最低能级上的宏观量子现象[1].1995年,Cornell等[2]通过激光冷却和射频蒸发冷却技术首次在170 nK的低温下获得了87Rb原子的BEC.同年,Ketterle等[3]利用塞曼減速技术冷却的原子束系统实现了23Na原子的BEC.之后,科学家们陆续实现了各种原子的BEC,使得其在物理研究中获得了重要的地位.
在超冷原子气体中,自旋轨道耦合(Spin-orbit coupling, SOC)的加入为探索新的量子现象提供了平台.自2011年实验上成功实现了带有SOC的87Rb BEC[4]以来,激发了人们对量子相变、拓扑激发以及自旋电子器件等的兴趣.实验上BEC被外势束缚,如光晶格势[5]、谐振子势[6]、同心耦合环形阱[7]、径向周期阱[8]等.在光晶格周期势中,非线性相互作用会明显改变布洛赫带的结构,使能带在第一布里渊区的边界处呈现出燕尾形状的环状结构[8].并且,晶格势和SOC的结合极大地扩展了冷原子的可调性,为研究BEC的相关物理特性提供了很好的平台,例如Bloch 振荡[9]、Landau-Zener 隧穿[10]、局域化等.
宇称-时间(parity-time, PT)对称是物理学的热门研究领域.1998年,Bender等[11]提出了一个具有PT对称的非厄米哈密顿量仍然具有完全实数的能谱.同时,非厄米系统中的PT对称势平衡了系统的增益和损耗.实验中,增益可通过使用原子激光器将原子注入冷凝物来实现[12],损耗采用激光束将原子激发到激发态,然后通过光子反冲将它们从凝聚物中喷射出来而实现[13].随着研究的进展,许多研究表明PT对称性在各个领域具有丰富的研究内容.2022年,Qin等[14]的研究表明,在PT对称伪自旋1/2系统中,与动量相关的平衡增益和损耗可以合成虚SOC,可以改变系统的能谱.Zhang等[15]通过引入虚势,从理论上研究了一维非厄米SOC Su-Schrieffer-Heeger模型的能带结构.
本文考虑一准二维SOC-BEC系统,用傅立叶配置法求解在PT对称晶格势下的线性能带结构,详细研究系统中各物理参量(如晶格的深度、自旋轨道耦合强度、拉比耦合强度等)对能带结构的影响.
1 理论模型与方法
1.1 理論模型
将一准二维SOC-BEC束缚在外势中,经无量纲处理后,在平均场近似下系统的动力学行为可用如下耦合Gross-Pitaevskii(GP)方程组描述[16]
iΨ↑t=[-2+V+g11Ψ↑2+
g12Ψ↓2]Ψ↑+iκ-Ψ↓+ΓΨ↓,
iΨ↓t=[-2+V+g21Ψ↑2+
g22Ψ↓2]Ψ↓+iκ+Ψ↑+ΓΨ↑,(1)
其中,Ψ↑↓=Ψ↑↓(r,t)表示波函数;r=(x,y),g11,g22和g12分别表征原子种内和种间相互作用强度,其具体表达式请参看文献[16];2=2x2+2y2是二维拉普拉斯算符;κ和Γ分别表示SOC强度和拉比耦合强度,±=/x±i/y.V为PT对称晶格势,可写为[17]
V(x,y)=VR(x,y)+iVI(x,y),(2)
满足V(x,y)=V*(-x,-y),即V(x,y)的实部VR为偶函数,虚部VI为奇函数.这里我们选择PT对称晶格势的实部和虚部分别为[18]
VR(x,y)=V0(cos2x+cos2y),(3)
VI(x,y)=V0×W0(sin(2x)+sin(2y)),(4)
其中,V0表示晶格深度,W0为PT对称晶格势虚部的相对大小.图1为该周期晶格势的实部和虚部的等值线图,其在空间呈现明显的周期结构.
1.2 线性能带结构
若寻找方程(1)形式为
Ψ↑↓(x,y,t)=φ↑↓(x,y)e-iμt
的定态解,则化学势μ和φ↑↓(x,y)满足
μφ↑=(-2+V+g11φ↑2+
g12φ↓2)φ↑+iκ-φ↓+Γφ↓,
μφ↓=(-2+V+g12φ↑2+
g22φ↓2)φ↓+iκ+φ↑+Γφ↑.
(5)
由于φ↑↓(x,y)和V(x,y)均为周期函数,其有界解可用布洛赫定理φ↑↓(x,y)=eik·r
φ↑↓(x,y)表示,其中波矢k=(kx,ky).若φ↑↓(x,y)为小量,则方程(5)中非线性项可以忽略,得到本征方程
μ(k)φ↑=-(+ik)2φ↑+Vφ↑+
iκ-φ↓+Γφ↓,
μ(k)φ↓=-(+ik)2φ↓+Vφ↓+
iκ+φ↑+Γφ↑.(6)
特征值μ(k)的集合构成布洛赫带(Bloch bands).
1.3 傅立叶配置法
一般情况下,很难得到本征方程(6)的精确解析解,可考虑对其进行数值求解,如有限差分法或傅立叶配置法等.傅立叶配置法是一种高精度的数值方法,在此做一简要介绍.
首先,将无界域(x,y)∈R2截断为有界域:-Lx/2≤x≤Lx/2,-Ly/2≤y≤Ly/2,其中Lx和Ly分别为x和y方向的区间宽度.然后,在此有界域上定义内积
f,g=∫f(x,y)g*(x,y)dxdy,
这里“*”表示复共轭.设
φ↑↓(x,y)=∑+∞m=-∞∑+∞n=-∞a↑,↓mnei(nk0x+mk0yy),
V(x,y)=∑+∞m=-∞∑+∞n=-∞bmnei(nk0x+mk0yy),
其中
k0x=2πLx, k0y=2πLy,
bmn=1LxLy∫Lx/2-Lx/2∫Ly/2-Ly/2V(x,y)
ei(nk0x+mk0yy)dxdy.
代入本征方程(6),并对求和指标进行截断后,得
μa↑mn=(-(ink0x)2-(imk0y)2+2nkxk0x+
2mkyk0y+(k2x+k2y))a↑mn+
∑+Nyl=-Ny∑+Nxj=-Nxbm-l,n-ja↑ij+
(c1-κnk0x+iκmk0y)a↓mn,
μa↓mn=(-(ink0x)2-(imk0y)2+2nkxk0x+
2mkyk0y+(k2x+k2y))a↓mn+
∑+Nyl=-Ny∑+Nxj=-Nxbm-l,n-ja↓ij+
(c2-κnk0x+iκmk0y)a↑mn.
n=-Nx,…,-1,0,1,…,Nx;
m=-Ny,…,-1,0,1,…,Ny.
其中c1=Γ-κkx+iκky,c2=Γ-κkx-iκky.此时本征方程(6)便转化为离散的矩阵形式
A=μ,
其中本征矢=a↑mna↓mn,矩阵A是(2Nx+1)×(2Ny+1)阶稠密方阵.随着Nx和Ny的增加,会导致存储量和计算量急剧增加.在后面计算中,取Ny=Nx=20.
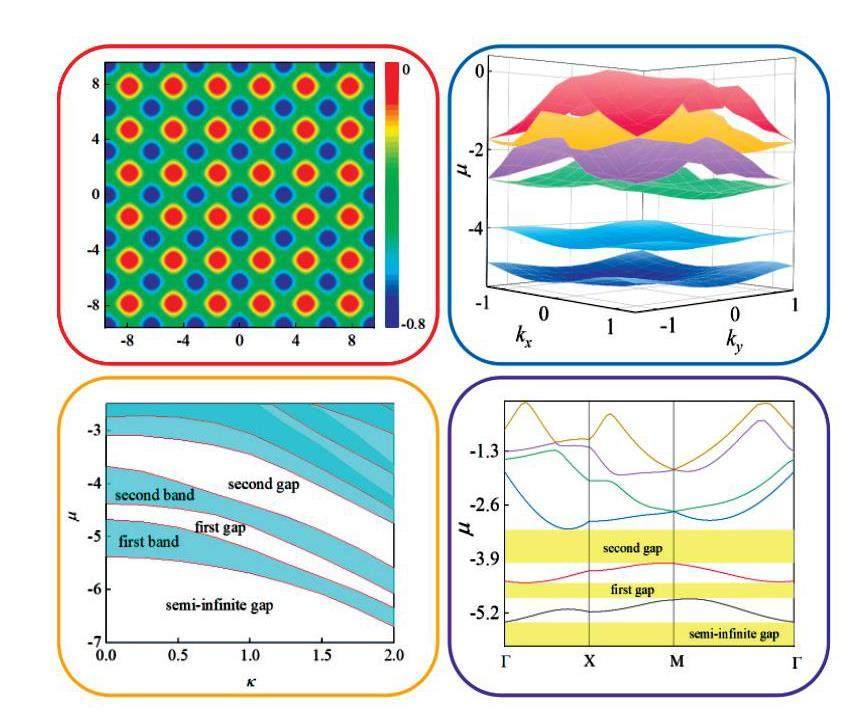
作为特例,图2给出了V0=-4,W0=0.1,κ=Γ=0.5时的布洛赫能带结构.从图3中可以看到一系列带隙将布洛赫能带分隔开来.通常将位于最低布洛赫能带下面的带隙称为半无限带隙,其它带隙依次称为第一带隙、第二带隙等等.这些带隙在系统中起着非常重要的作用.图3中,半无限带隙的区域约为μ<-5.42,第一带隙区域约为0.484<μ<-4.47.
图3a和3b分别是图2a沿kx和ky方向的投影图.从图3可以看出,布洛赫能带沿kx方向关于kx=0不对称,而沿ky方向关于ky=0对称.
(V0=-4,W0=0.1,κ=Γ=0.5)
in PT symmetric lattice potential
(V0=-4,W0=0.1,κ=Γ=0.5)
2 数值结果及分析
下面我们系统地计算晶格深度V0,PT对称晶格势的虚部W0,SOC强度κ以及拉比耦合强度Γ的变化对能带结构的影响.
2.1 PT对称晶格势对能带结构的影响
数值结果表明,PT对称晶格势的深度V0与W0对能带结构有着明显的影响.图4给出了能带结构随 V0的变化,所选参数为W0=0.1,κ=Γ=0.5.从图4可以看出,当晶格深度V0很小时,能带结构出现了交叠,此时只存在半无限带隙,第一带隙和第二带隙均没有打开.随着晶格深度V0的增加,第一能带的下边沿和上边沿均上升,但能带宽度变窄.当V0增大至2.37时,第一带隙开始出现且其宽度随V0的增大而增大.当V0大于2.47时,第二带隙开始出现,且逐渐变宽.
图5给出了V0=-4,κ=Γ=0.5时能带结构随W0的变化.从图5可以看到,随着W0的增大,
半无限带隙的上边沿逐渐增大.当W0<0.4时,
时,第一能带和第二能带的宽度变化并不明显,但第一带隙和第二带隙的宽度则随W0的增大而明显变窄.当W0增大至临界值0.4时,所有能带出现交叠,此时只存在半无限带隙.
2.2 自旋轨道耦合强度对能带结构的影响
自旋轨道耦合强度κ也是影响能带结构的重要参数之一.图6给出了能带结构随κ的变化,所选参数为V0=-4,W0=0.1,Γ=0.5.从图6可以看出,随着κ的增大,第一能带和第二能带的上边沿均逐渐减小,能带整体向下移动,其宽度也逐渐变窄.但当κ增加到一定值时,它们的宽度变化不再明显.在此过程中,第一带隙和第二带隙始终存在.
2.3 拉比耦合对能带结构的影响
图7给出了V0=-4,W0=0.1,κ=0.5时拉比耦合强度Γ对能带结构的影响.从图7可以看出,在所选参数条件下,第一能带的上下边沿均随Γ的增大而减小,且两边沿大致呈平行状.值得注意的是,当Γ<0.32时,图7所示的第一帶隙并不存在(事实上此时图7所示第二带隙应称为第一带隙).当Γ>0.32时,系统产生图7所示第一带隙,且其宽度随着Γ的增大而增大.但当Γ足够大时,第一带隙的宽度变化不再明显.图7中所示第二带隙的变化则与此有点相反.随着Γ的增加,第二带隙的宽度明显变窄.当Γ>0.96时,第二带隙消失.该结果表明拉比耦合强度对于系统的带隙结构也有着重要的影响.在实验中,可通过调节其值控制和改变系统的能带结构.
3 结论
数值研究了PT对称晶格势下准二维SOC-BEC中的线性能带结构.在平均场近似下,BEC的动力学行为可用耦合GP方程组来描述.用傅立叶配置法数值求解了不同参数下的能带结构.结果表明,随着晶格深度V0的增加,第一能带的上下边沿均上升,但能带宽度变窄.PT对称势的虚部W0存在临界值,当W0小于临界值时,第一能带和第二能带的宽度变化并不明显;W0大于临界值时所有能带出现交叠.随着SOC强度κ的增大,第一能带和第二能带的上边沿均逐渐减小,能带整体向下移动,其宽度也逐渐变窄.系统的能带和带隙结构也受拉比耦合强度Γ的影响.故实验中可通过调节这些参数来改变能带结构.
参考文献:
[1] 漆伟,李明,郭晓刚.三体作用下玻色-爱因斯坦凝聚体中的PT-对称孤子[J].西北师范大学学报(自然科学版),2022,58(6):66.
[2] ANDERSON M H,ENSHER J R,MATTHEWS M R,et al.Observation of Bose-Einstein condensation in a dilute atomic vapor[J].Phys Rep,1995,269(5221):198.
[3] 梁青青,周小燕,李好财.有限温度下含三体相一经作用的玻色-爱因斯坦凝聚体的集体激发特性[J].西北师范大学学报(自然科学版),2023,59(4):54.
[4] LIN Y J,GARCIA K J,SPIELMAN I B.Spin-orbit-coupled Bose-Einstein condensates[J].Nature,2011,471:83.
[5] KUHN S,JUDD T E.Transport of dipolar Bose-Einstein condensates in a one-dimensional optical lattice[J].Phys Rev A,2013,87(2):023608.
[6] XU X Q,HAN J H.Spin-orbit coupled Bose-Einstein condensate under rotation[J].Phys Rev Lett,2011,107(20):200401.
[7] MALET F,KAVOULAKIS G M,REIMANN S M.Mixtures of Bose gases confined in concentrically coupled annular traps[J].Phys Rev A,2012,81(1):013630.
[8] WANG Y J,WEN L,GUO H,et al.Spin-orbit-coupled Bose-Einstein condensates in radially periodic potentials[J].J Phy Soc Jpn,2019,88(2):024005.
[9] MACHHOLM M,PETHICK C J,SMITH H.Band structure,elementary excitations,and stability of a Bose-Einstein condensate in a periodic potential[J].Phys Rev A,2003,67(5):053613.
[10] JI W,ZHANG K,ZHANG W,et al.Bloch oscillations of spin-orbit-coupled cold atoms in an optical lattice and spin-current generation[J].Phys Rev A,2019,99(2):023604.
[11] KONOTOP V V,KEVREKIDIS P G,SALERNO M.Landau-Zener tunneling of Bose-Einstein condensates in an optical lattice[J].Phys Rev A,2005,72(2):023611.
[12] BENDER C M,BOETTCHER S.Real spectra in non-Hermitian Hamiltonians having PT symmetry[J].Phys Rev Lett,1998,80(24):5243.
[13] ROBINS N P,FIAL C,JEPPESEN M,et al.A pumped atom laser[J].Nat Phys,2008,4(9):731.
[14] LI J,HARTER A K,LIU J,et al.Observation of parity-time symmetry breaking transitions in a dissipative Floquet system of ultracold atoms[J].Nat Comm,2019,10(1):855.
[15] QIN J L,ZHOU L,DONG G J.Imaginary spin-orbital coupling in parity-time symmetric systems with momentum-dependent gain and loss[J].New J Phys,2022,24(6):063025.
[16] WANG Q Q,TU P,MA J P,et al.Vector gap solitons of spin-orbit-coupled Bose-Einstein condensate in square optical lattice[J].J Phys B,2024,57(6):065201.
[17] MENG H J,WANG J,SHI Y R,et al.Vector gap solitons of spin-orbit-coupled Bose-Einstein condensate in honeycomb optical lattices[J].Phys Rev E,2023,108(3):034215.
[18] SCHWARZ L,CARTARIUS H,MUSSLIMANI Z H,et al.Vortices in Bose-Einstein condensates with PT-symmetric gain and loss[J].Phys Rev A,2017,95(5):053613.
[19] XIE J N,SU Z K,CHEN W C,et al.Defect solitons in two-dimensional photonic lattices with parity-time symmetry[J].Opt Comm,2014,313(0030-4018):139.
(責任编辑 孙对兄)
