主动关联马赫-曾德尔干涉仪中多参数相位估值的极限

王强 曾杰 焦高锋 袁春华

摘要： 基于量子费歇尔信息和量子费希尔信息矩阵理论 ， 研究了三端口输入的主动关联马赫-曾德尔（Mach-Zehnder， MZ）干涉仪在两种不同输入态下的相位估值极限.研究结果得到 ， 在单个端口输入任意光场的情况下 ， 利用相位平均和量子费歇尔信息矩阵理论消除了输入光场的涨落对相位估值极限的影响;而在双端口输入相干态的情况下 ， 无法消除光场涨落对估值极限的影响 ， 且相位估值极限依赖于输入的双相干光的初始相位.

关键词：主动关联马赫-曾德尔干涉仪;  量子费歇尔信息矩阵;  相位估值;  非线性分束器

中图分类号： O431.2    文献标志码： A    DOI： 10.3969/j.issn.1000-5641.2022.02.016

Limit of multi-parameter phase estimation in an actively correlated Mach-Zehnder interferometer

WANG Qiang ，  ZENG Jie ，  JIAO Gaofeng ，  YUAN Chunhua

（School of Physics and Electronic Science， East China Normal University， Shanghai  200241， China）

Abstract： In this paper， the phase estimation limits of an active-related Mach-Zehnder interferometer with three port inputs and two different input states was studied using quantum Fisher information and quantum Fisher information matrix theory. In the case of an arbitrary light field input to a single port， the effect of the input field fluctuation on the limit of phase estimation is eliminated by the theory of phase averaging and the quantum Fischer information matrix. In the case of a dual port input coherent state， the effect of the fluctuating light field on the estimation limit cannot be eliminated， and the phase estimation limit depends on the initial phase of the two input coherent states.

Keywords： actively correlated Mach-Zehnder interferometer;  quantum Fisher information matrix;  phase estimation;  nonlinear beam splitter

0  引言

干涉儀的相位灵敏度是一个颇受关注的研究热点. 在给定具体的探测方案后 ， 依赖误差传播理论[1]可以给出该方案下干涉仪的相位灵敏度;然而该方法无法历遍所有可能的测量方案 ， 因此无法确定干涉仪在理想探测手段下的最佳相位灵敏度. Braunstein 和 Caves 提出的量子费歇尔信息理论可以完美地解决上述问题[2]. 量子费歇尔信息只依赖于特定的输入状态 ， 而不依赖于特定的探测方案.此时相位灵敏度的最终界限由量子克拉美罗界（Quantum Cramér-Rao Bound ， QCRB）决定：∆2ϕ⩾ 1/F ， 其中 F 为量子费歇尔信息[2-3]. 当考虑到实验中存在着多个未知参数时 ， 需要将量子费歇尔信息扩展至量子费歇尔信息矩阵 （Quantum Fisher Information Matrix， QFIM）， 即可得某个未知参数的 QCRB—∆2ϕ⩾ 1/F 其中 FM 为 QFIM[4].

马赫-曾德尔干涉仪（MZ 干涉仪）和 SU（1， 1）干涉仪是当前精密测量领域中主流研究的两类干涉仪 . MZ 干涉仪虽然可以容纳强光场 ， 但在采用经典光源（相干光）时其相位灵敏度极限受限于标准量子极限（Standard Quantum Limit， SQL）：∆2ϕ⩾ 1/n ， 其中n 代表干涉仪中光子数[5]. 研究者们采用量子光源 ， 如压缩态[5]、 N00N 态[6]、双 Fock 态[7]、双模压缩态[8]等 ， 来突破 SQL. SU（1， 1）干涉仪[9] 采用非线性分束器 ， 如光参量放大器（Optical Parametric Amplifier， OPA）， 来替换 MZ 干涉仪中的线性分束器 ， 实现相位灵敏度的提高 . SU（1， 1）干涉仪可以逼近海森堡极限 （Heisenberg Limit， HL）：∆2ϕ⩾ 1/n2[4]. 因此 SU（1， 1）干涉仪在理论上 [10-21]和实验上[22-31]都得到了广泛的研究 .但是 SU（1， 1）干涉仪无法容纳强光场导致的其相位灵敏度绝对精度的不够高.近年来 ， 结合这两类干涉仪 ， 有研究者提出了一类 MZ 干涉仪的变型 —主动关联马赫-曾德尔 （Actively Correlated Mach-Zehnder， ACMZ）干涉仪[32]. ACMZ 干涉仪与传统的 MZ 干涉仪相比 ， 在输入上 ， 其中一个端口输入强光场 ， 另外一个端口输入由 OPA 输出的双模压缩态的一模;在输出上 ， 输出的一模通过元器件 OPA 与双模压缩态的另外一模相结合 ， 实现了放大输出. ACMZ 干涉仪与传统的 SU（1， 1）干涉仪相比 ， 干涉仪中光子数量过少的问题得到了改善.

本文研究了两种不同输入态下 ACMZ 干涉仪相位测量的 QCRB.在单端口输入光场的情况下， 通过两类方式得到了相同的最优 QCRB;在双相干态的情况下 ， 给出了最佳初始相位和的表达式 ， 并证明了初始相位波动对 QCRB 的影响能力 ， 以及其受到 ACMZ 干涉仪参数的影响.

1   ACMZ 干涉仪模型

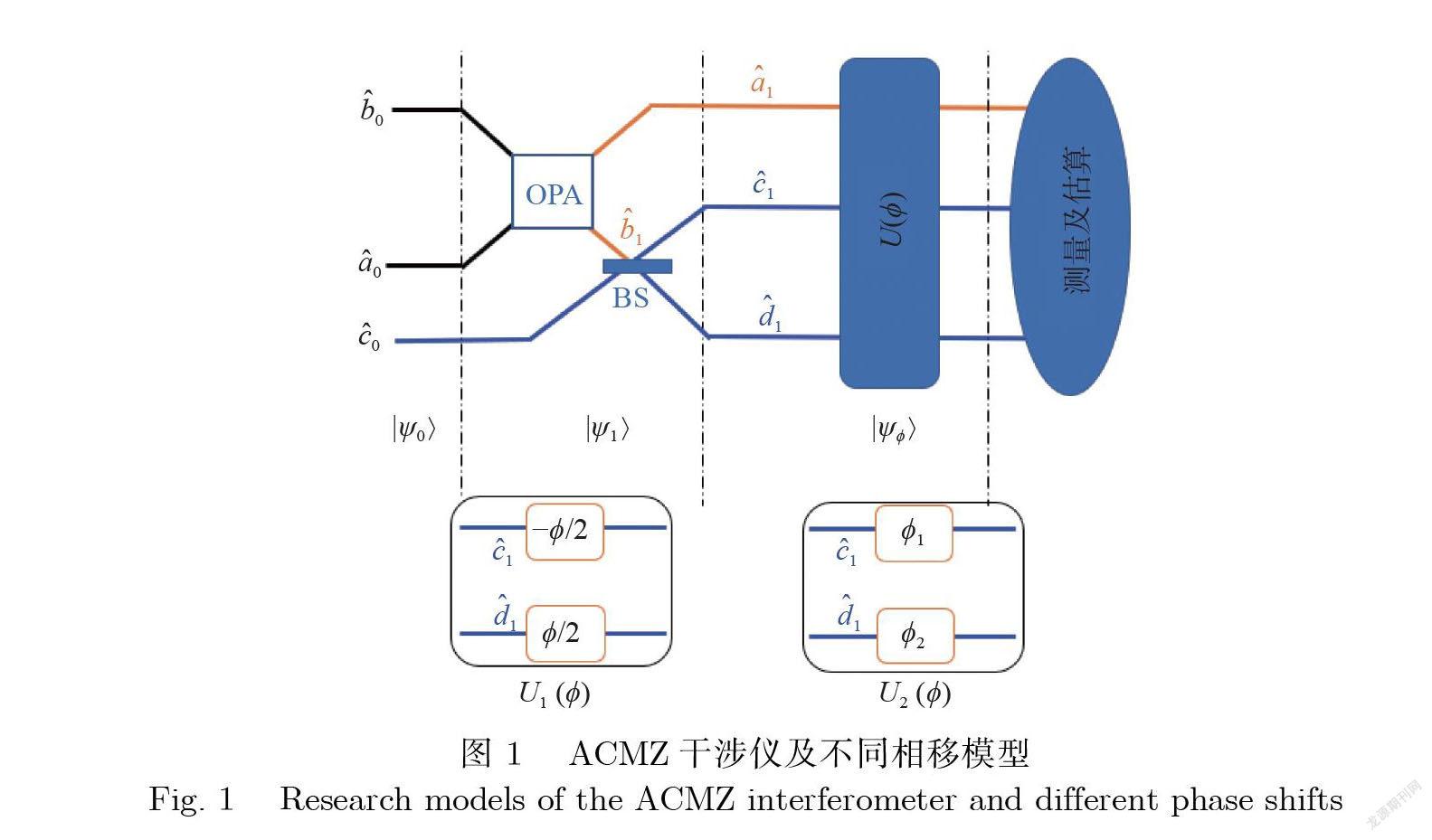
本文的 ACMZ 干涉仪主要组成如图 1所示：线性分束器（Beam Splitter， BS）的一个输入端口（模式 c）输入强泵浦场 ， 另一个输入端口（模式 b）输入由非线性分束器 OPA 产生的双模压缩态的一个模式; ACMZ 干涉仪的4种模式用湮灭算符 i ，  i ， cˆi ， dˆi （i =0， 1）来描述;在 c 通道以及 d 通道嵌入未知相移作为本文的估值参数 ， 即未知相移U1（ϕ）均匀分布于两臂 ， 两臂均存在未知相移 U2（ϕ）.

相移算符 U （ϕ）依据未知相移的分布有着不同的构建方式.第一类：当未知相移是平均分布于 c 通道和 d 通道时 ， 相移算符 U1（ϕ）= eiϕ D  ， 其中算符gˆD = （dˆ dˆ1 − cˆ cˆ1）/2. 第二类：在 c 通道和 d 通道同时存在着不同的未知相移ϕ1和 ϕ2 ， 该情况下 ACMZ 干涉仪模型的相移算符可以写为  U2（ϕ）= eiϕ1  1 eiϕ2d^ d^1  = eiϕS  S eiϕd D  ， 其中算符 gˆS = （dˆ dˆ1+ cˆ cˆ1）/2 ， 相移表述为ϕS = ϕ1+ ϕ2 ， ϕD = ϕ2 −ϕ1. 值得注意的是， 上述第一类为单参数估值 ， 第二类为双参数估值. 在海森堡表象下， ACMZ 干涉仪的输入输出关系为

式（1）中 ， G 代表 OPA 的增益系数 ， 它与g 满足关系 G2 − g2 =1 ;θOPA 为 OPA 相位; T 和 R 分别为 BS 的透射系数以及反射系数. 注意： c 端口能容纳的光场场强远强于 a 端口和 b 端口的光场场强.

2  单端口输入光场

2.1  单参数估值

本节将研究 ACMZ 干涉仪在 BS 一端输入任意态ρˆχ（模式c）， 其余输入端口（模式 a 和模式 b）输入真空态|0⟩⟨0|的情况下单参数估值 U1（ϕ）的结果.

此时测量态为纯态. 利用纯态量子费歇尔信息计算公式 F =4[⟨gˆ2⟩− ⟨gˆ⟩2]可得

其中 ， Nc = ⟨ψ0|cˆ cˆ0|ψ0⟩ ， Vc = ⟨ψ0| （ cˆ0）2|ψ0⟩− ⟨ψ0|cˆ cˆ0|ψ0⟩2 ， 它们分别为 c 端口输入光场光强度以及光强涨落. 取 T = R =0.5时 ， 得到最大量子费歇尔信息值

然而正如 Jarzyna 等所提到的 ， 当直接采用量子费歇尔信息计算公式时 ， 很可能会过多地估计外部资源的利用[33]. 因此需要通过相位平均的思路 ， 来避免过多估计外部资源的可能. 将输入态在粒子数态上做展开 ， 有

其中， n⟩代表粒子数态 ， 下标c、a、b 代表输入端口. 那么相位平均以后其输入态可以表示为[33]

其中 ， A、B、C 代表3 个端口 ， VθA = eiθ y ， VθB = eiθ y ， VθC = eiθ y ， Pn = |cn|2 ， ∑Pn = 1. 那么相位平均后， 输出态的密度矩阵为

其中 ， |ψn⟩= U （ϕ） BT ，G |00n⟩ ， BT ，G 代表 OPA 和 BS 的共同作用. 注意上述过程中只对输入态相位取了平均， 而没有对 OPA 相位θOPA 做平均.这说明在测量的过程中依旧可以使用 OPA 相位θOPA 对应的额外资源 ， 这与 SU（1， 1）干涉仪是一致的[8]. 随后利用量子费歇尔信息的凸性[34] ， 可知相位平均后的量子费歇尔信息

其中， F （|ψn⟩）代表态|ψn⟩的量子费歇尔信息. 其相应公式为

因此相位平均后单参数估计的量子费歇尔信息

依据式（9）可以看出 ， 当仅 c 端口输入光场 ， 其余端口均输入真空态时 ， 取 T = R =0.5时可以得到最大的量子费歇尔信息

比较式（9）与式（2）， 可以发现 ， 相位平均后消除了光場强度涨落项 Vc 对量子费歇尔信息的影响;然而比较式（10）与式（3）发现 ， 量子费歇尔信息最大值没有发生改变.显然， 当T = R =0.5且固定 OPA 的增益 G 时 ， 量子费歇尔信息与输入光场的光强呈正相关 ， 且不依赖于 c 端口输入光场ρˆχ的结构 ， 即输入光场涨落 Vc 项不能提高 ACMZ 干涉仪的最佳相位灵敏度.此时提高 ACMZ 干涉仪的相位灵敏度的最佳方式是提高 c 端口输入光场的场强. 这与 MZ 干涉仪以及 SU（1， 1）干涉仪中的结论相类似.

2.2  双参数估值

在2.1节 ， 已经得到了单参数估值的量子费歇尔信息.但需要注意的是 ， 在2.1 节中存在这一个预先的假设ϕS = ϕ/2 −ϕ/2 =0;然而在更多的情况中 ， 未知相移ϕS， ϕD 均是未知的 .此时 ， 即使仅有 1个参数为所需估值参数 ， 也需将原来单参数估值问题扩展至多参数估值领域.本节在继续维持输入态不变的情况下 ， 研究双参数估值的情况下的 QCRB.

在多参数估值领域 ， 其 QCRB 是通过 QFIM 得到的[4]. 本文选取参数ϕS 和ϕD ， 此时对应的 QFIM 为2×2矩阵

其中， 矩阵元Fij = 4[⟨gˆigˆj⟩− ⟨gˆi⟩⟨gˆj⟩]， i， j = S， D .在本文中， 所需要估值的参量为ϕD .这时依据 QFIM 求得的 QCRB 为[4]

依据矩阵元表达式可知 FDS = FSD ， 那么从式（12）可见 ， 当且仅当 FDS = 0 时 ， FSS对ϕD 无影响. 即此时无需关心ϕS 是否已知 ， ϕS 对ϕD 的估值精度没有影响. 上述情况在 MZ 干涉仪中亦可以见到.综上可以看出 ， 式（12）显示了非对角元在双参数估值中的作用. 当忽略非对角元在参数估值中的作用时 （隐晦地表示在实验前就假设了ϕS 是一个已知量）， 将会把 FDD 直接作为ϕD 的 QCRB 对应的量子费歇尔信息， 从而高估估值精度极限.

将输入态|χ⟩⊗ |0⟩⊗ |0⟩代入 QFIM 矩阵元的表达式中 ， 那么最终获得 QFIM 矩阵元

将式（13）代入式（12）， 最终得到 QCRB

通过式（14）对透射系数 T 偏导 ， 可得在 T = R =0.5时 ， QCRB 取得最佳值

比较式（9）与式（14）可以发现 ， 不同于相位平均方法 ， 采用 QFIM 方法时 ， 光强涨落依旧影响着 QCRB.但是进一步比较式（10）和式（15）可以发现 ， 两类方法均于 T = R =0.5时取得最优 QCRB， 此时光场涨落项 Vc 在其中不起作用， 采用不同方法最终得到的最优 QCRB 一致.

3  双端口输入光场

3.1  最优 QCRB

由式（15）和式（10）得出了 ， 在 a 端口和 b 端口输入真空态的情况下 ， ϕD 的最佳 QCRB 不受 c 端口输入光场涨落 Vc 的影响 ， 只与光场场强有关. 下面考虑在 c 端口输入相干态的同时 ， 在 a 端口输入一个不同相干态 ， 探究该情况下 ACMZ 干涉仪的 QCRB.

输入态描述为

其中 ， α=  e  iθc ， β=  e  iθa  ， θa 、θc 分别代表两个相干态携带的初始相位信息.在双相干态输入情况下 ， QFIM矩阵元将得到修改 ， 计算结果为

其中 ， Θ= θOPA +θa +θc ， Na = ⟨ψ0|   0|ψ0⟩ ， Va = ⟨ψ0| （  0）2|ψ0⟩− ⟨ψ0|   0|ψ0⟩2. 这3 项分别是双相干光携带的初始相位、  a 端口输入相干光光强及涨落. 求 QCRB 得

其中

令相干光初始相位Θ= 0 ， 当且仅当 BS 的参数 T = R =0.5 ， 式（19）才取到最大值

比较式（19）与式（20）可以发现 ， 当 T = R =0.5时 ， 光场的涨落项 Va ， Vc 将不再影响 QCRB.该结论与2.2 节的结论相同. 比较式（15）与式（20）发现 ， 当双端口输入相干态时 ， 最优 QCRB 得到了提高 .对式（20）进行进一步分析可得 ， FCoh ，max 主要由两项贡献组成： Nag2项和 Nc （G2+ g2）项. 比较这两项可以发现 ， 提高 Nc 项能更好地提高FCoh ，max .同时考虑到对 ACMZ 干涉仪而言 ， 其 c 端口输入光场的光强可以远强于 a 端口输入光场光强 ， 即 Nc ≫ Na ， 故可以认为 a 端口输入相干光对最优 QCRB 的提升有限 ， 最优 QCRB 主要还是由 c 端口输入相干光光强 Nc 及 OPA 增益系数G 所决定.此外依据式 （19）发现 ， 当Θ 不为 0时 ， BS 的透射系数 T 取任意值 ， 光场的涨落项 Va ， Vc 都将影响到 QCRB 的取值.

3.2  相干光初始相位和对 QCRB 影响

本节将在保留初始相位和Θ 下进一步探究始相位和Θ 的最优值及其对 QCRB 的影响. 将式（19）对Θ求导 ， 可得最佳初始相位和ΘOpt满足条件

其中 ， 等号右边第一项 f （T）= （T − R）/4代表 BS 对 sinΘOpt 的影响能力;第二项 N （g， Na ， Nc ）表述为

代表光场及 OPA 对sinΘOpt 的影响能力. f （T）与 N （g， Na ， Nc ）共同作用影响相干光携带初始相位和的最佳值sinΘOpt .依据式（22）， 可以发现 ， 当 T = R =0.5时 ， 输入光场光强及光场涨落对ΘOpt无影响 ， 此时ΘOpt = kπ ， k 为整数 ， 对应的量子费歇尔信息由式（20）给出.

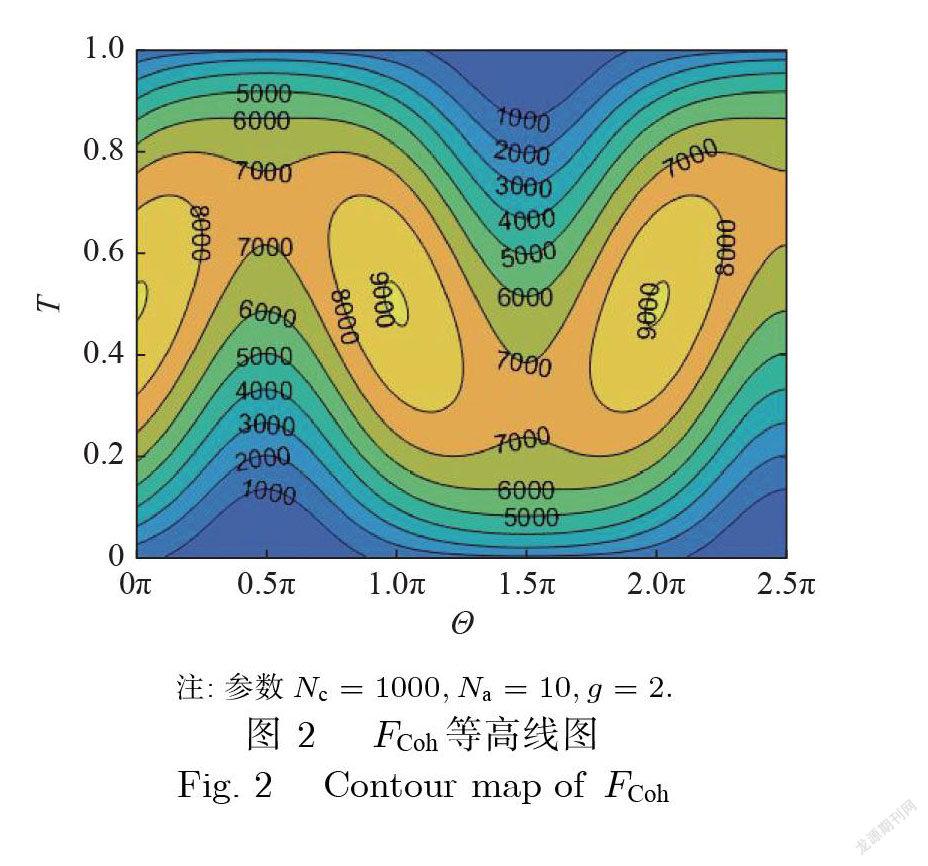
为进一步探究初始相位和Θ 对量子费歇尔信息影响 ， 利用式（19）做量子费歇尔信息在不同的透射系数 T 下与相干光初始相位和Θ的关系分析， 结果见图 2.由图2可以看出， Θ對FCoh的影响能力依赖于 T 值：当 T ⩾0.5时 ， Θ在[0， π]处对 FCoh的影响能力弱于Θ 在[π， 2π] 的影响能力; T ⩽0.5时 ， Θ在 [π， 2π]处对FCoh的影响能力弱于Θ在[0， π]的影响能力.

4  结论

本文研究了单端口输入任意态、双端口输入双相干态这两种情况下 ACMZ 干涉仪的相位估值极限 .对于单端口输入任意态 ， 通过相位平均方法可以消除光场涨落项 Vc 对 QCRB 的影响;利用 QFIM 方法时 ， 仅当 T = R =0.5时 （取得最优 QCRB 的条件）， 光场涨落项 Vc 对 QCRB 无影响;通过相位平均方法和 QFIM 方法得到的最优 QCRB 相同， 与输入光场强度呈正相关.

对于双端口输入相干态（Nc ≫ Na ）， 在双相干光初始相位和Θ =0情况下 ， 最优 QCRB值在 T = R =0.5处取得 ， 该值仅由光场强度及 OPA 增益系数决定 ， 不依赖于光场涨落项 Va ， Vc ;在双相干光初始相位和Θ  0时 ， 对任意 T ， 最优 QCRB均依赖于光场涨落项 Va ， Vc .此外本文还给出了最佳初始相位和ΘOpt 的表达式 ， Θ对量子费歇尔信息的影响能力受到 BS 透射系数 T 的影响：当 T =0.5时 ， ΘOpt = kπ ， QCRB 不受输入光场性质影响. 目前实验上对 ACMZ 干涉仪的研究正在展开[35] ， 本文的理论结果可对 ACMZ 干涉仪的研究工作提供参考.

[參考文献]

[1]KAY S M. Fundamentals of Statistical Signal Processing： Estimation Theory [M]. Upper Saddle River， New Jersey： Prentice-Hall Inc，1993.

[2]BRAUNSTEIN S L， CAVES C M. Statistical distance and the geometry of quantum states [J]. Physical Review Letters， 1994， 72（22）：3439-3443.

[3]HELSTROM C W. Quantum Detection and Estimation Theory [M]. New York： Academic Press， 1976.

[4]YOU  C L， ADHIKARI  S，  CHI Y X， et al. Multiparameter estimation with single photons-linearly-optically generated quantum entanglement beats the shotnoise limit[J]. Journal of Optics， 2017， 19（12）：124002.

[5]CAVES C M. Quantum-mechanical noise in an interferometer [J]. Physical Review D， 1981， 23：1693-1708.

[6]DOWLING J P. Quantum optical metrology – the lowdown on high-N00N states [J]. Contemporary Physics， 2008， 49（2）：125-143.

[7]CAMPOS R A， GERRY C C， BENMOUSSA A. Optical interferometry at the Heisenberg limit with twin Fock states and parity measurements [J]. Physical Review A， 2003， 68（2）：023810.

[8]ANISIMOV P M， RATERMAN G M， CHIRUVELLI A， et al. Quantum metrology with two-mode squeezed vacuum： Parity detection beats the Heisenberg limit [J]. Physical Review Letters， 2010， 104：10360210.

[9]YURKE B， MCCALL S L， KLAUDER J R. SU（2） and SU（1， 1） interferometers [J]. Physical Review A， 1986， 33（6）：4033-4054.

[10]PLICK W N， DOWLING J P， AGARWAL G S. Coherent-light-boosted， sub-shot noise， quantum interferometry [J]. New Journal of Physics， 2010（12）：083014.

[11]OU Z Y. Enhancement of the phase-measurement sensitivity beyond the standard quantum limit by a nonlinear interferometer [J]. Physical Review A， 2012， 85（2）：023815.

[12]MARINO A M， CORZO TREJO N V， LETT P D. Effect of losses on the performance of an SU（1， 1） interferometer [J]. Physical Review A， 2012， 86（2）：023844.

[13]LI D， YUAN C H， OU Z Y， et al. The phase sensitivity of an SU（1， 1） interferometer with coherent and squeezed-vacuum light [J]. New Journal of Physics， 2014， 16：073020.

[14]GABBRIELLI M， PEZZE L， SMERZI A. Spin-mixing interferometry with Bose-Einstein condensates [J]. Physical Review Letters， 2015， 115（16）：163002.

[15]CHEN Z D， YUAN C H， MA H M， et al. Effects of losses in the atom-light hybrid SU（1， 1） interferometer [J]. Optics Express， 2016， 24（16）：17766-17778.

[16]SPARACIARI C， OLIVARES S， PARIS M G A. Gaussian-state interferometry with passive and active elements [J]. Physical Review A， 2016， 93（2）：023810.

[17]LI D， GARD B T， GAO Y， et al. Phase sensitivity at the Heisenberg limit in an SU（1， 1） interferometer via parity detection [J]. Physical Review A， 2016， 94（6）：063840.

[18]GONG Q K， HU X L， LI D， et al. Intramode-correlation-enhanced phase sensitivities in an SU（1， 1） interferometer [J]. Physical Review A， 2017， 96（3）：033809.

[19]GIESE E， LEMIEUX S， MANCEAU M， et al. Phase sensitivity of gain-unbalanced nonlinear interferometers [J]. Physical Review A， 2017， 96（5）：053863.

[20]HU X， LI D， CHEN L Q， et al. Phase estimation for an SU（1， 1） interferometer in the presence of phase diffusion and photon losses [J]. Physical Review A， 2018， 98（2）：023803.

[21]CAVES C M. Reframing SU（1， 1） interferometry [J]. Advanced Quantum Technologies， 2020， 3（11）：1900138.

[22]JING J T， LIU C J， ZHOU Z F， et al. Realization of a nonlinear interferometer with parametric amplifiers [J]. Applied PhysicsLetters， 2011， 99（1）：011110.

[23] HUDELIST F， KONG J， LIU C J， et al. Quantum metrology with parametric amplifier-based photon correlation interferometers [J].Nature Communications， 2014（5）： Article number 3049.

[24] CHEN B， QIU C， CHEN S Y， et al. Atom-light hybrid interferometer [J]. Physical Review Letters， 2015， 115（4）：043602.

[25] QIU C， CHEN S Y， CHEN L Q， et al. Atom-light superposition oscillation and Ramsey-like atom-light interferometer [J]. Optica，2016， 3（7）：775-780.

[26] LINNEMANN D， STROBEL H， MUESSEL W， et al. Quantum-enhanced sensing based on time reversal of nonlinear dynamics [J].Physical Review Letters， 2016， 117（1）：013001.

[27] LEMIEUX S， MANCEAU M， SHARAPOVA P R， et al. Engineering the frequency spectrum of bright squeezed vacuum via groupvelocity dispersion in an SU（1， 1） interferometer [J]. Physical Review Letters， 2016， 117（18）：183601.

[28] MANCEAU  M，  LEUCHS  G，  KHALILI  F，  et  al. Detection  loss  tolerant  supersensitive  phase  measurement  with  an  SU（1， 1）interferometer [J]. Physical Review Letters， 2017， 119（22）：223604.

[29] ANDERSON B E， GUPTA P， SCHMITTBERGER B L， et al. Phase sensing beyond the standard quantum limit with a variation onthe SU（1， 1） interferometer [J]. Optica， 2017， 4（7）：752-756.

[30] GUPTA P， SCHMITTBERGER B L， ANDERSON B E， et al. Optimized phase sensing in a truncated SU（1， 1） interferometer [J].Optics Express， 2018， 26（1）：391-401.

[31] DU W， JIA J， CHEN J F， et al. Absolute sensitivity of phase measurement in an SU（1， 1） type interferometer [J]. Optics Letters，2018， 43（5）：1051-1054.

[32] JIAO  G  F  ZHANG  K  Y，  CHEN  L  Q，  et  al. Nonlinear  phase  estimation  enhanced  by  an  actively  correlated  Mach-Zehnderinterferometer [J]. Physical Review A， 2020， 102（3）：033520.

[33] JARZYNA M， DEMKOWICZ-DOBRZANSKI R. Quantum interferometry with and without an external phase reference [J]. PhysicalReview A， 2012， 85（1）：018011.

[34] FUJIWARA A， IMAI H. A fibre bundle over manifolds of quantum channels and its application to quantum statistics [J]. Journal ofPhysics A， 2008， 41（25）：255304.

[35] DU W，  KONG  J，  JIA  J，  et  al. SU（2）-in-SU（1， 1） nested  interferometer [EB/OL]. （2020-04-29）[2021-05-06]. https：//arxiv.org/ pdf/2004.14266v1.pdf.

（責任编辑：李艺）