斜裂纹定量检测的全光学检测技术研究

邓 进， 刘艺灏， 李海洋， 李 兵， 潘强华， 张晓彤， 那雪璐

(1. 中国特种设备检测研究院，北京 100029; 2. 中北大学先进制造技术山西省重点实验室，山西 太原 030051)

0 引 言

表面缺陷是金属材料失效主要形式之一，会对结构的工作安全造成严重威胁。对于表面缺陷的检测一直以来是无损检测研究的重要内容，尤其是对微裂纹的定量检测，直接影响结构的性能、可靠性和使用寿命。一般来说，实际表面缺陷具有角度、宽度、深度呈随机分布的特点，给表面缺陷的定量检测造成了困难。激光超声检测技术具有非接触且高灵敏度的特点，可在待测样品表面激励表面波，对于斜裂纹的定量检测十分适用。

关于激光超声的研究和应用，始于20世纪60年代，迄今已取得了丰富的研究成果。White[1]最早在固体中成功使用脉冲激光激励得到了超声波。紧接着Askaryan[2]在White研究的基础上，发现了在液体中同样能够激发出超声波。Scruby[3]提出了激光超声的正交力偶模型。Rose[4]推导了激光作用于弹性半空间的点源模型，为激发激光超声的热弹机制提供了理论基础。Spicer[5]基于热传导方程研究了激光光源的时间和空间参数对激光超声波的影响。Bernstein[6]基于横向力偶极子建立了激光线源二维模型。Achenbach[7-8]运用傅里叶-拉普拉斯双变换解析法求解，建立了更为完善的激光线源二维模型。

国内在激光超声领域也开展了很多研究。陈龙[9]使用弹性常数描述金属箔材力学性能。刘增华[10]采用全光学型激光超声检测系统，显示了激光Lamb波信号的传播特性以及激光Lamb波与表面缺陷之间的作用规律。张月影[11]通过研究各模态超声波在裂纹不同闭合状态下的到达时间，发现了裂纹闭合顺序与裂纹宽度相对应这一规律。王纪俊[12]采用有限元方法建立了激光超声的热弹有限元数值模型。

激光超声技术作为一种新兴的无损检测技术，在探伤领域有着巨大的应用价值。赵燕飞[13]分析了表面缺陷深度与超声敏感特征的定量关系。张颖志[14]实现了对材料表面缺陷的粗略定位。丁一珊[15]等获得了无裂纹、表面裂纹、其他裂纹下的温度变化和声波信号,得到了裂纹检测受声表面波衰减特性影响的结论。郭海洋[16]利用零差干涉仪检测了涂层影响下长宽尺寸的表面缺陷信号,计算出了表面缺陷深度的大小。李海洋[17]根据表面波在表面缺陷处的透射和反射阈值现象，提出了测量表面缺陷深度的临界频率法，并证明了透射和反射阈值大小与表面波的传播距离以及材料的材质无关。以上成果多数集中于表面缺陷深度与位置的定量检测，但对于斜裂纹的检测研究较少。

本文采用有限元仿真手段分析了激光超声表面波与斜裂纹相互作用机理。激光超声表面波在斜裂纹处发生反射与透射现象，该现象与倾斜角度和裂纹深度与宽度有关，导致透射激光超声表面声信号携带了斜裂纹的几何信息。本文基于对斜裂纹处透射系数的分析，实现了激光超声表面波与斜裂纹相互作用的分析，为激光超声在工业检测中实际应用提供了理论依据。

1 理论分析与仿真模型

有限元分析是以实际物理模型为基础，再利用数学近似方法，划分成有限个网格单元，求解得到对应近似解，再利用近似解去按照标准方法逼近真实系统。有限元方法由于其对于复杂结构的适应性以及对于各种物理问题的可应用性特点，在仿真模拟求解复杂物理问题中得到了广泛的应用[18]。本文采用COMSOL软件作为有限元仿真工具。由于有限元仿真是一个相对理想的状态，为了计算声表面波在材料中的传播，忽略传播过程中阻尼的作用，瞬态的热传导方程的有限元形式表示为：

根据激光光源时间和空间参数表1，可绘制出激励源直观的时间和空间函数如图1所示。

表1 激光光源时间和空间参数

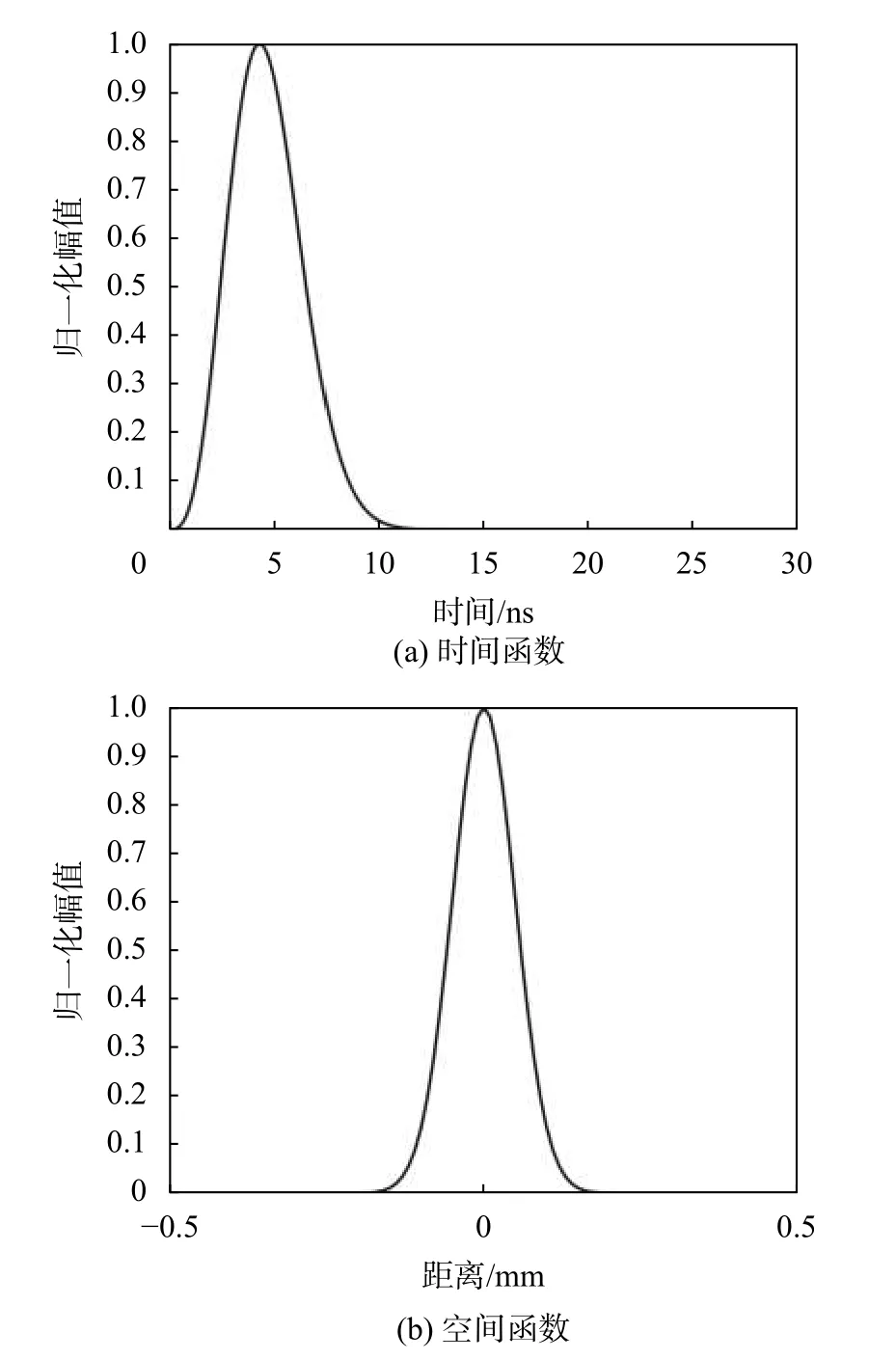
图1 激光光源时间与空间函数

本文采用铝合金作为仿真材料，在有限元软件COMSOL中建立激光超声二维仿真模型，其材料物理参数如表2所示。建立长度为30 mm，厚度为5 mm的铝板，并设置深度范围为0.2 mm到1.2 mm，宽度为0.2 mm到0.6 mm的斜裂纹，仿真扫查模型如图2所示。

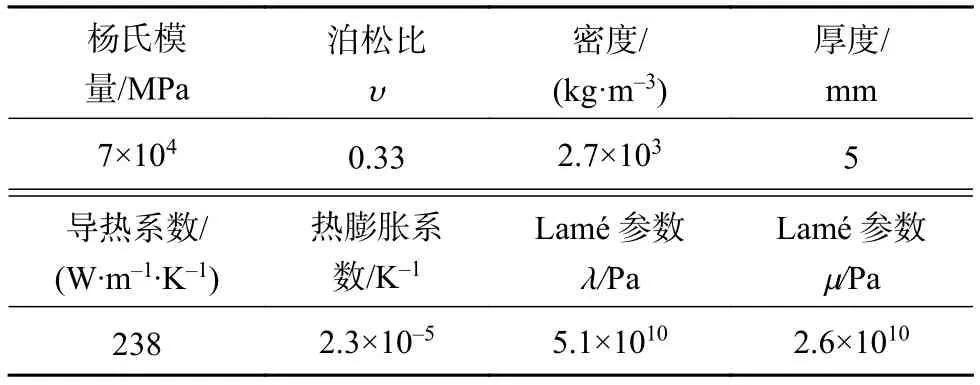
表2 物理参数

图2 扫查示意图

为保证能量在两个相邻网格间连续传播，在仿真中需选取合适的网格大小。一般来说，网格大小小于超声波波长的四分之一的空间分辨率，才能够满足仿真弹性波传播的精度要求。本文所使用的脉冲激光，产生的超声波中心频率可以用如下公式进行估算：；相对应的波长即为：，根据计算公式同时综合考虑计算效率本文中采用的三角形网格边长为8.0×10-4mm。同时为了获得精确的求解，需要在仿真中设置合适的时间步长，一般来说，所取的时间步长越短，获得的解精确度越高，但是相应的计算所需的时间也会变长，影响计算效率。本文采用公式计算得到合适的时间步长。根据中心频率的大小，本文所采取的时间步长为 1.507 1×10-8s。

2 仿真结果与分析

脉冲激光照射在试件材料的表面，在物体内部形成一个温度梯度场，进而激发出热应力作为超声波的激发力源。这一应力在物体内部以瞬态脉冲的形式传播，从而形成超声波在固体介质传播。如图3所示，为 1 μs、2 μs、3 μs、4 μs不同时刻下的超声波声场云图。

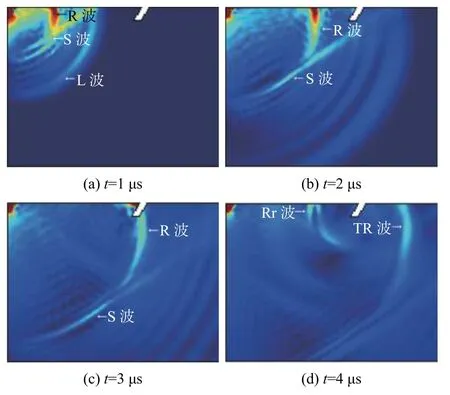
图3 不同时间下的激光超声波传播图像(θ=120°)

由图3可以看出，激光激发出超声波是一个很短暂迅速的物理能量转化过程。图3（a）为1 μs时刻的超声波声场云图，此时超声波远离斜裂纹，从图中可以清晰地看到横波（S 波）、纵波（L波）以及表面瑞利波(R 波)。其中R波沿材料上表面传播，而S 波和L 波在材料内部进行传播，并且其传播方向具有一定的指向性。激光激励R波沿着材料表面继续传播遇到斜裂纹，如图3(c)所示。直达表面波与斜裂纹相互作用，一部分能量在斜裂纹左边缘发生反射形成反射回波(Rr Wave)，另一部分能量沿着斜裂纹壁传播到另一侧形成透射表面波(TR Wave)，如图3（d）所示。由于透射波携带了斜裂纹的几何信息，因此可通过分析透射波来实现裂纹的表征。本文建立不同角度、深度与宽度的斜裂纹进行检测研究，其角度范围为 22.5 °～150 °，深度范围为 0.2～1.2 mm，宽度范围为 0.2～0.6 mm，且变化方向如图4所示。

图4 斜裂纹角度变化方向示意图

将无裂纹模型与携带有宽度W为0.2 mm，角度θ为90°，深度d为1 mm的裂纹模型的直达波与透射波显示如图5所示。

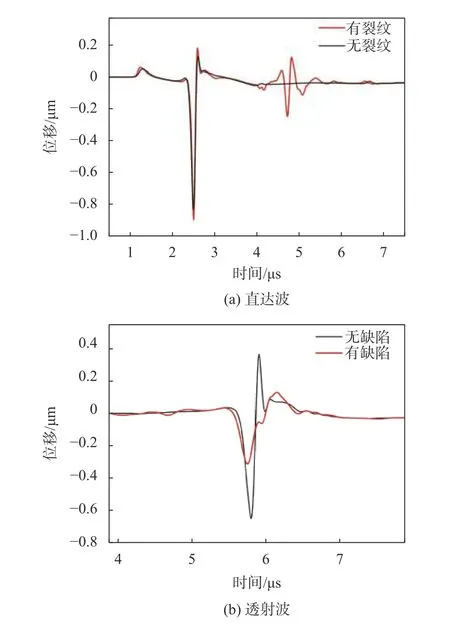
图5 激光超声直达波与透射波位移时域波形

如图5（a）所示的直达表面波是由激光激励源激发出的表面波沿着材料表面传播直接被探测点接收到的波形，因此不包含有斜裂纹信息。

将相同宽度W为0.2 mm，相同角度θ，不同深度d的裂纹处的透射波频谱显示如图6所示。

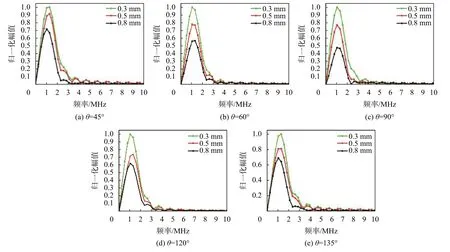
图6 不同深度斜裂纹下的激光超声透射波频谱

如图 6 所示为倾斜角度分别为 45°、60°、90°、120°、135°时不同深度斜裂纹下的激光超声透射波频谱图。从频谱可以看出随着斜裂纹深度的增加，透射表面波的最大频谱幅值逐渐减小，且中心频率保持不变。同时通过对比不同倾斜角度下的频谱幅值变化，也可以发现斜裂纹倾斜角度为90°时的透射波频谱最大幅值随深度的变化最大。相同宽度为0.2 mm，相同深度为0.8 mm，不同倾斜角度裂纹处的透射声波时域波形如图7所示。

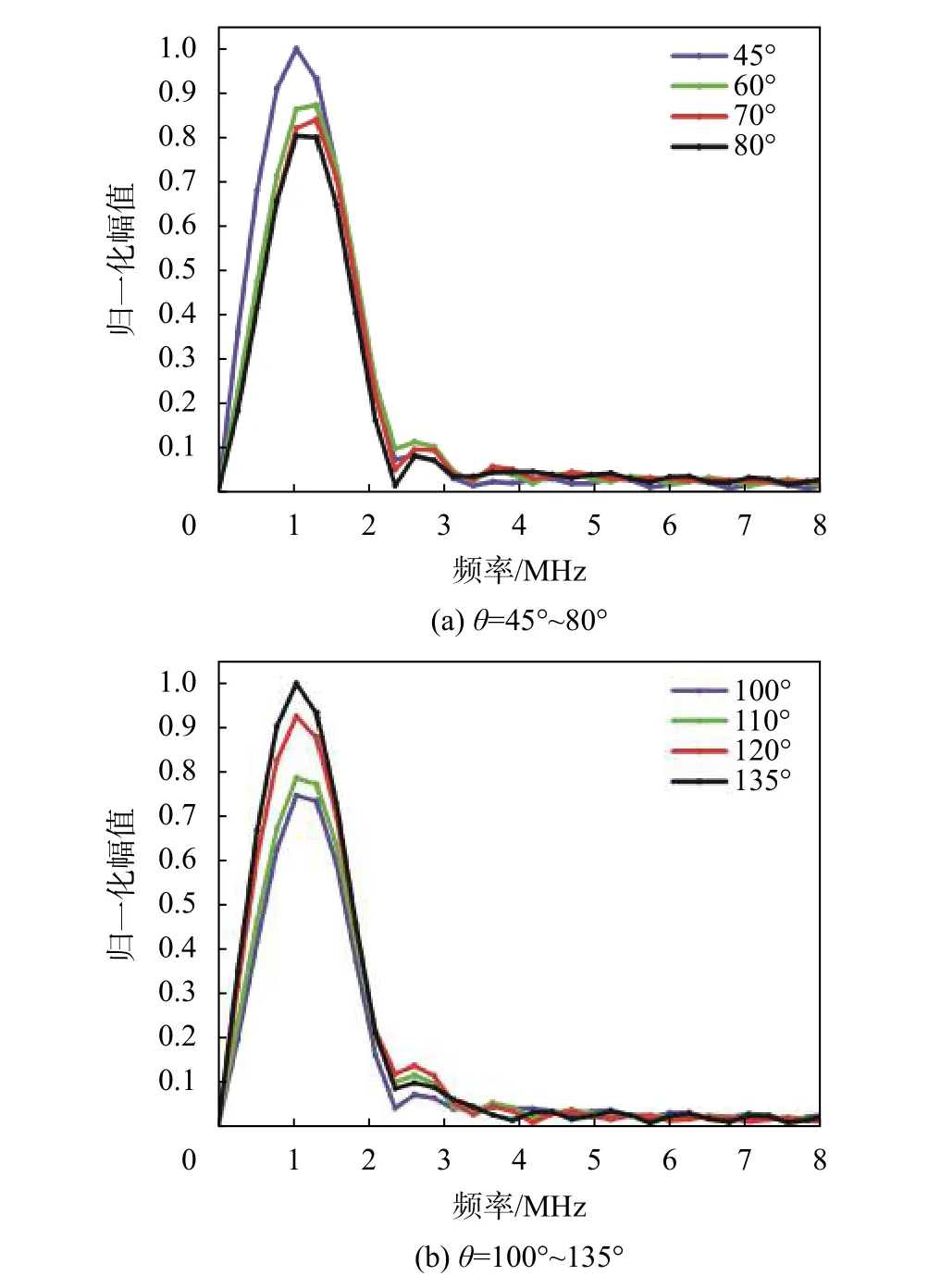
图7 不同角度斜裂纹下的透射波频谱

如图 7 所示为倾斜角度分别为 45°、60°、70°、80°和 100°、110°、120°、135°的斜裂纹下的激光超声透射波频谱图。从图中可以看出，随着斜裂纹倾斜角度的增大，在45°～80°范围内，透射表面波的最大频谱幅值逐渐减小；在100°～135°范围内，透射表面波的最大频谱幅值逐渐增大。倾斜角度为90°，相同深度，不同宽度裂纹处的透射声波频谱如图8所示。

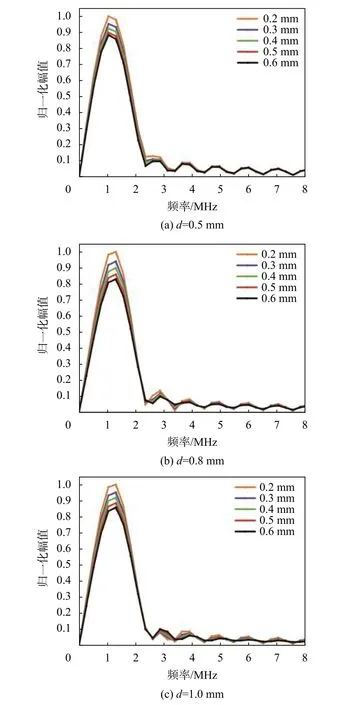
图8 不同宽度斜裂纹下的激光超声透射波频谱

深度为0.8 mm，相同倾斜角度，不同宽度裂纹处的透射声波频谱如图9所示。

图9 不同宽度斜裂纹下的激光超声透射波频谱

综合图8、9可以看出，透射表面波的最大频谱幅值随着宽度的增大逐渐减小，且这种变化与深度、倾斜角度无关。

因此本文采取声表面波的透射现象来实现对斜裂纹深度与角度的判断。为了减少由于激光激发能量的不同而造成的测量误差，定义透射系数为频谱中透射声波最大幅值At与频谱中入射声波最大幅值大小Ai的比值，表达为T=At/Ai。本文采用该透射系数来表征斜裂纹的深度、角度与宽度，绘制不同深度、不同角度的透射系数变化曲线如图10所示。

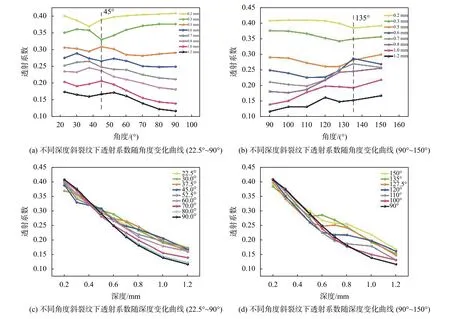
图10 不同角度与深度下的透射系数

如图 10（a）、（b）所示，当斜裂纹深度小于等于0.5 mm时，斜裂纹倾斜角度对于透射系数的影响较小。以0.5 mm为临界深度值，斜裂纹深度大于0.5 mm且倾斜角度在45°～135°范围内时，斜裂纹的透射系数随角度呈线性变化。在45°～90°范围内时随着角度的增大，透射系数逐渐减小；在90°～135°范围内时，随着角度的增大，透射系数逐渐增大。图10(c)、(d)所示为不同倾斜角度的斜裂纹随深度变化的曲线，从图中可以看出具有不同倾斜角角度的斜裂纹的透射系数随深度都呈线性变化，随着深度变大，透射系数逐渐变小。并且随着深度的增加，深度的变化对于透射系数的影响逐渐减小，曲线斜率趋于平缓。

如图11所示为以深度为X轴，角度为Y轴，透射系数为Z轴的三维等高线图，同时按照图例所示的颜色分布也反映了透射系数的数值大小。从图中可以清晰直观地看出透射系数随深度X轴的减小逐渐增大的上升趋势。观察角度Y轴，也可以发现，在深度较大透射系数较低的区域等高线以90°左右为中心向上弯曲，在深度较小透射系数较大区域等高线与角度Y轴接近平行，这也说明了角度在斜裂纹深度较小时对透射系数的影响较小的规律。

图11 深度-角度-透射系数三维等高线图

从图12(a)、(b)可以看出透射系数随着宽度的增大透射系数逐渐减小，且这种变化与深度、倾斜角度无关。

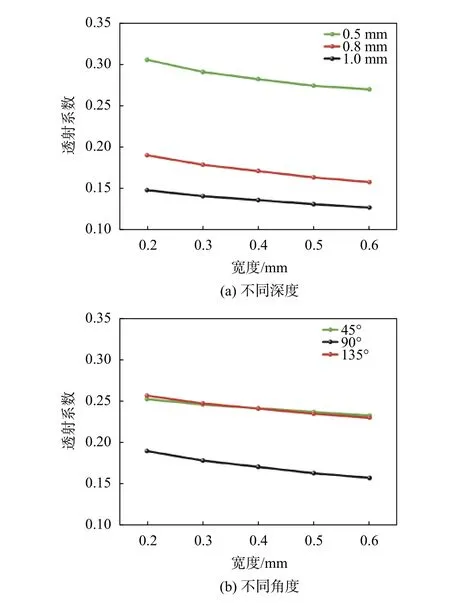
图12 斜裂纹透射系数随宽度变化曲线

针对角度对透射系数影响较大的区域，本文采用三次多项式拟合对仿真数据进行拟合。图13(a)、(b)、(c)、(d)、(e)所示为斜裂纹深度分别为 0.6 mm、0.7 mm、0.8 mm、1 mm、1.2 mm，角度范围在 45°～135°内，激光超声表面波透射系数-斜裂纹角度的三次多项式拟合曲线。

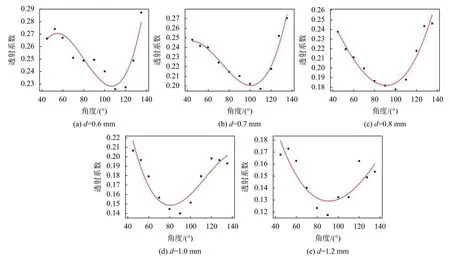
图13 透射系数-角度三次多项式拟合曲线

如图14所示的深度拟合曲线中的离散数据点为不同深度下的所有角度对应的透射系数的平均值。图15中的离散数据点为不同角度、深度下的所有宽度对应的透射系数的平均值。对透射系数与深度、宽度、角度进行拟合，所得到的三次多项式拟合曲线数据与实际仿真数据的残差平方和与拟合度分别如表3、4、5所示。

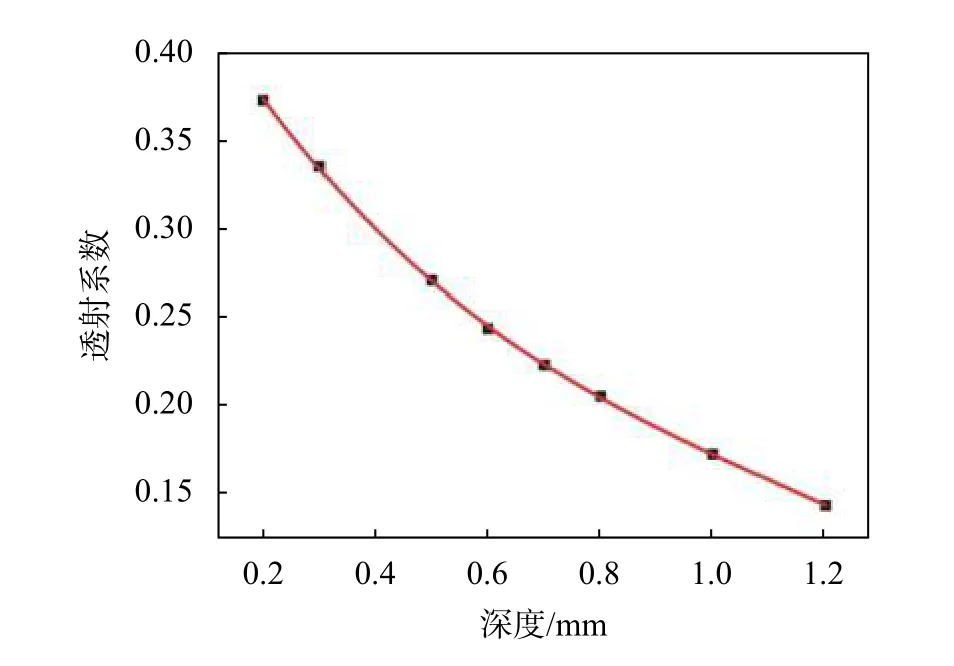
图14 透射系数-深度三次多项式拟合曲线

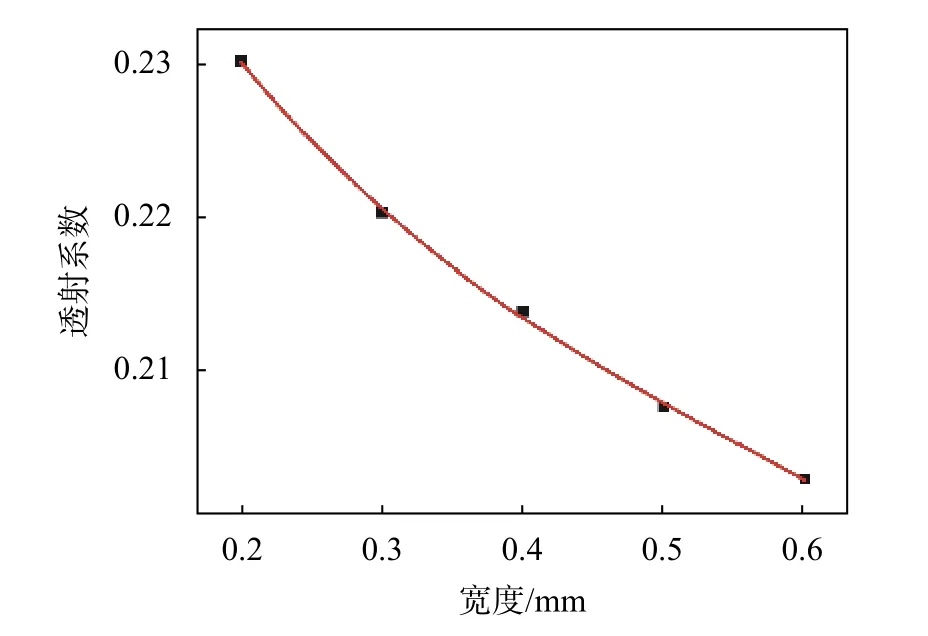
图15 透射系数-宽度三次多项式拟合曲线

表3 深度拟合误差

表4 宽度拟合误差

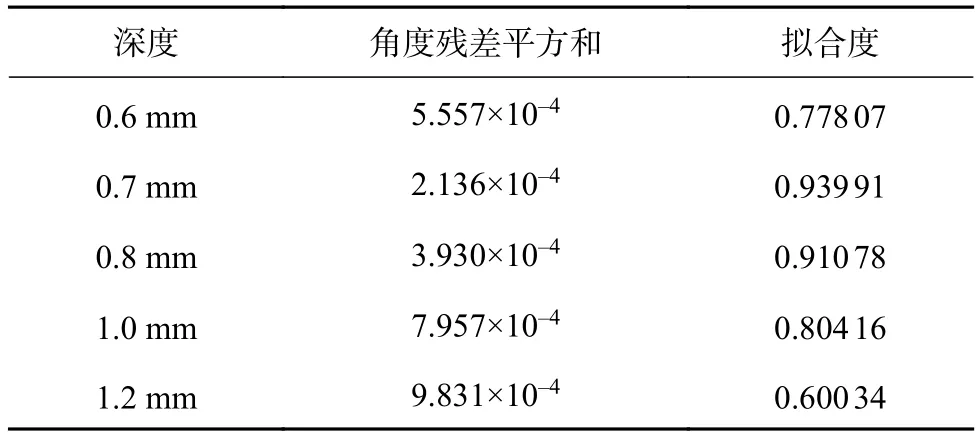
表5 角度拟合误差

由表3、4、5可知，深度为 0.7 mm、0.8 mm时的角度拟合与深度拟合、宽度拟合效果均较好。因此本文通过三次多项式拟合方程来分别描述透射系数与角度θ、深度d、宽度W之间的关系：

公式(7)、(8)描述了不同深度时透射系数随角度的变化关系，如下图所示为公式(7)、(8)的导函数曲线图。

由导函数图 16可以看出，在角度 45°～135°的范围内，透射系数变化曲线分别以100.8°，91.2°为对称轴开口向上弯曲，呈对称线性关系。

3 结束语

本文建立了斜裂纹与激光超声作用的二维仿真模型，对不同深度、不同角度和不同宽度的斜裂纹进行了仿真计算，并实现了采用透射系数对斜裂纹几何参数的分析。研究结果表明：激光超声表面波透射系数随斜裂纹深度呈线性变化，深度越大，透射系数越变小，且这种变化与倾斜角度无关。当斜裂纹深度大于 0.5 mm且倾斜角度在 45°～90°和90°～135°范围内时，透射系数与倾斜角度呈线性关系。同时随着宽度的增大透射系数逐渐减小，且这种变化与深度、倾斜角度无关。证明通过探测斜裂纹透射系数的方法对于斜裂纹的角度、深度与宽度的检测是有效可行的。

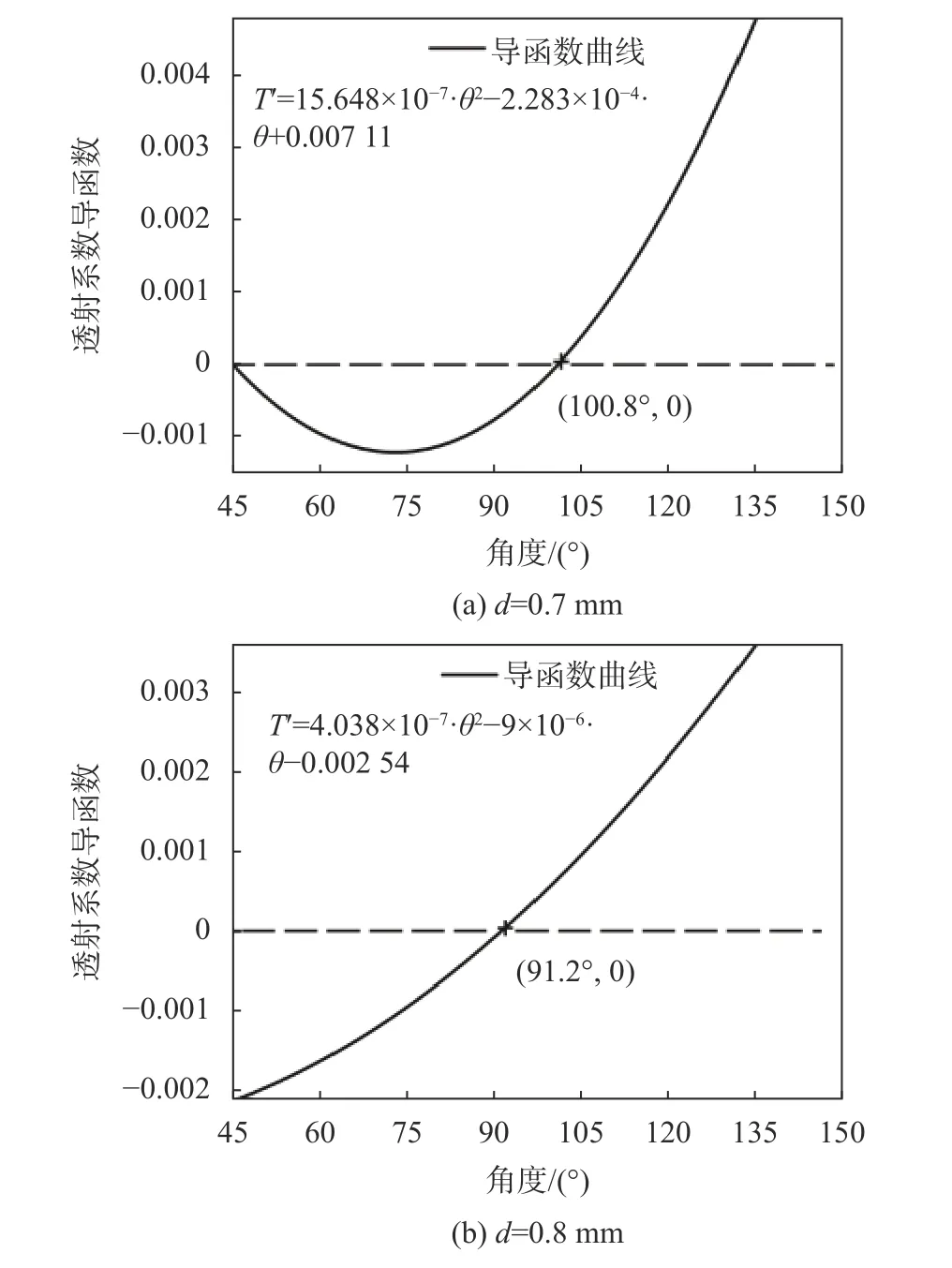
图16 透射系数导函数曲线图