泡沫钻水平井岩屑颗粒的运移规律研究

张 杰， 李荣鑫， 李 鑫， 周成华， 张 珍， 李翠楠

1油气藏地质及开发工程国家重点实验室 2西南石油大学石油与天然气工程学院 3中国石化西南石油工程有限公司钻井工程研究院 4中国石油西南油气田分公司工程技术研究院

0 引言

随着定向井及水平井在油气勘探开发中广泛应用，研究人员对大斜度及水平井中岩屑的输送越来越关注[1]。泡沫钻井液由于其结构的黏滞特性，具有良好的携岩性能，对于定向井增斜段以及水平井大斜度/水平段的井眼清洁、减少井眼环空的堵塞和卡钻，从而达到安全快速钻进的目的有着至关重要的作用[2]。

国内外多位学者对泡沫钻井液以及其携带岩屑的性能进行了大量的理论与实验研究，发现当岩屑在倾斜圆管中运动时将会有三种运动形式共同存在，即静止床、滑移床和悬移层，并建立了适用于大斜度/水平段的三层流动数学模型[3- 8]。目前对于井筒气—液两相流的研究[9- 10]主要集中在单一气液混合物的研究上，没有考虑泡沫这种具有特殊流变模型的流体。因此，本文针对泡沫这种具有特殊流变性的流体模型，对水平井稳定泡沫钻井大斜度/水平段的传输规律进行探讨。分析了每一个井段的岩屑传输特点,建立了相应的岩屑传输模型。对环空中的岩屑床厚度随井斜角变化的分布曲线进行了模拟，并分析了各个流动参数对环空中岩屑床厚度的影响规律。

1 模型的建立及求解

根据不同的环空水力参数条件，环空中的岩屑运动方式可以划分为悬移质和推移质(接触质、跃移质和层移质统称为推移质)[11]。推移质运动实质上是一种包括了岩床颗粒之间的剪切运动以及岩屑颗粒同周围的流体之间的剪切运动。随着环空中流体流速的继续增大，岩屑就可以保持悬移状态。

根据Tomren等[3]的研究成果，按照不同井斜角的范围将整个井段划分为了三个区域，按照不同井斜角时的岩屑运移特征和岩屑床种类划分为三个部分：垂直段(0°～30°)、过渡段(30°～60°)以及大斜度/水平段(60°～90°)。

1.1 环空的泡沫携岩流动过程模型假设

为了方便泡沫携岩流动数学模型的建立以及模型的计算，首先对环空泡沫携岩流动过程进行如下假设：

(1)泡沫流动为稳定流动，且气液两相之间不存在滑脱现象。

(2)泡沫流体的液相不可压缩，泡沫流体的压缩性只取决于气相。

(3)岩屑颗粒的粒径和圆球度为常数，同时在各层中均匀分布。

(4)不考虑钻柱转动的影响。

1.2 岩屑输送模型

1.2.1 模型的假设条件

建立泡沫流体井筒流动模型时，做出以下假设和忽略：

(1)稳定泡沫在井筒内流动不会发生相间滑脱现象，即均相流动。

(2)井口处的泡沫质量为最大泡沫质量98%，井底的泡沫质量为最小泡沫质量50%。

(3)整个井筒内的流动为层流，并且已达到充分发展状态，流动过程为稳定绝热过程。

(4)不考虑钻柱转动的影响。

1.2.2 流动模型的建立

基于质量和动量守恒基本方程[12- 15]，考虑上述基本假设条件，得到各截面的岩屑输运模型。

1.2.2.1 垂直/近垂直段(0°～30°)

岩屑在垂直段岩屑主要受到四个不同的力作用：重力，浮力，拖拽力以及上举力，如图1所示。

图1 垂直/近垂直井段岩屑受力示意图

FB+FDcosθ+FL-G>0

(1)

式中：FB—岩屑的浮力，N;FD—拖拽力，N;G—重力，N。

1.2.2.2 过渡段(30°～60°)

根据临界井斜角理论，过渡段的岩屑主要以推移质的形式存在，环空上部的为悬浮岩屑颗粒，该区域各层的受力情况如图2所示。

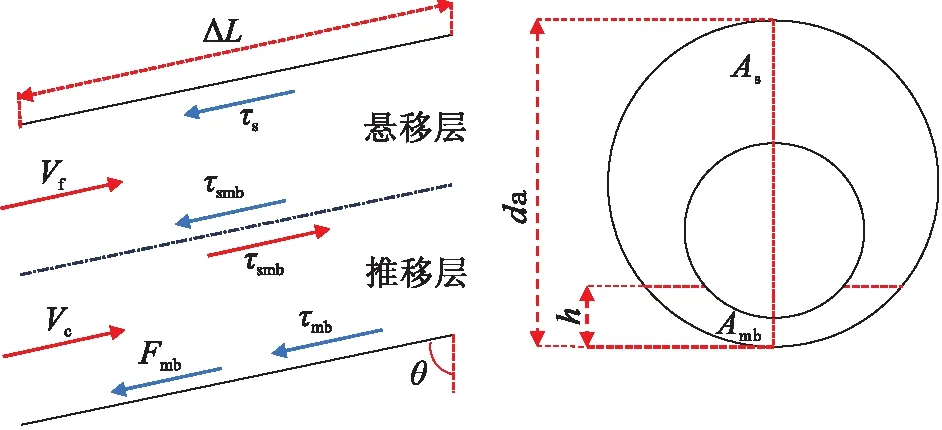
图2 过渡段岩屑传输双层流动模型

υfAfCf+υcAcCc-υcAbCb=υtAa

(2)

式中：vfAfCf—单位时间内悬移层运走的岩屑质量，kg；vcAcCc—单位时间内推移质运动带走的岩屑质量，kg；vcAbCb—单位时间内形成的新的岩床质量，kg；vtAa—钻头单位时间内钻进而产生的岩屑总量，kg。

ΔpAs=τsSsΔL+τsmbSsmbΔL+ρsgAsΔLcosθ

(3)

式中：Δp—压降,MPa;ΔL—微元井段长度，m;τs—悬移层与壁面的剪切应力，MPa；τsmb—悬移层与推移质之间的切应力，MPa；ρs—岩屑密度，kg/m3;θ—井斜角,(°)。

ΔpAmb+τsmbSsmbΔL=τmbSmbΔL+ρmbgAmbΔLcosθ+FmbΔL

(4)

式中：τmb—推移质与壁面的剪切应力，MPa；ρmb—岩屑密度，kg/m3；Fmb—推移质与壁面之间的滑动摩擦力，N。

1.2.2.3 大斜度/水平段(60°～90°)

在倾斜/水平段主要存在三个流动层：环空下部的固定岩床层，固定床上部的移动岩床以及在环空上部的悬移层，如图3所示。

图3 大斜度/水平段岩屑传输三层流动模型

υsAsCs+υmbAmbCmb+υsbAsbCsb-υυAmbCmb=υtAa

(5)

式中：vsAsCs—单位时间内悬移层运走的岩屑质量，kg；vmbAmbCmb—单位时间内移动岩床运动带走的岩屑质量,kg，kg；vsbAsbCsb—单位时间内固定岩床运动带走的质量；vvAmbCmb—形成的新的岩床的质量，kg；vtAa—钻头单位时间内钻进而产生的岩屑总量，kg。

(6)

(7)

式中：τmbsb—移动岩床与固定岩床之间的切应力，MPa；Fmb—移动岩床与壁面之间的滑动摩擦力，N；Fmbsb—移动岩床与固定岩床之间的滑动摩擦力，N。

该模型与Ozbayoglu等[12]建立的模型进行了比较，针对不同井段建立了相应的求解方程其适用范围更广。此外，在研究中将三层理论应用于泡沫钻井岩屑输送。该模型改进了Nguyen和Rahman[4]研究的三个液压模型的岩屑输送且形式简单，简化了计算机求解的工作，通过分段建模，其适用性更强。

1.3 模型求解

对于垂直/近垂直段，可以直接根据模型进行求解。对于过渡段和大斜度/水平段，首先需要分别对它们的动量守恒方程进行变形，然后再进行求解。

1.3.1 过渡段

(8)

(9)

(10)

1.3.2 大斜度/水平段

(11)

通过计算岩屑床面积占井筒总面积的比例来表征岩屑床的厚度，可以更清晰地分析影响岩屑床厚度的因素之间的关系。从而确定合理的钻井参数，减少岩屑床层厚度，节约钻井成本，减少钻井事故。

可以利用反推法对岩屑床厚度进行迭代计算。首先，假设岩屑床厚度为h，得到各个对应参数的值，然后代入到控制方程组中进行计算。如果能满足公式(10)和式(11)，那么假设的岩屑床厚度就是正确的值，否则，需要假设一个新的h并且重复以上计算。

2 实例计算与分析

2.1 基础数据

为了验证模型的正确性，根据基础数据编写了相应的计算过程，用于环空岩屑运移规律分析。基础数据具体如下：

井身结构数据：井垂深为1 600 m，水平位移453 m，井眼直径215.9 mm，偏心度0.6，钻速7.6 m/h。井口数据：地面温度21 ℃，地温梯度2.7 ℃/100 m，井口回压0.7 MPa。岩屑参数：岩屑密度2.56 g/cm3，岩屑平均粒径7 mm，岩屑圆球度0.8，井底泡沫质量56%，井底的泡沫流量1.04 m3/min。

2.2 岩屑运移规律分析

根据以上数据，本文利用所建立的理论模型，对稳定泡沫的岩屑传输能力的各个影响因素进行了分析。具体分析如图4～图10所示。

图4为井底流量为1.04 m3/min时环空中各流动层的无因次岩屑床厚度随着井斜角变化的分布规律。从图4中可以看出，在整个井段存在着三种环空岩屑传输的传输方式，即大斜度/水平段的三层流动，过渡段的两层流动以及近垂直段的单层悬浮混合流动。首先，在大斜度/水平段(60°～90°)，可以看到很明显地存在着三个流动层，即在环空最底部的固定床层，固定床层上部的移动床层以及在环空中上部的悬浮层，而且随着井斜角θ的减小，环空返速在轴向方向上分量的会逐渐增大，导致了固定床的厚度逐渐减少，但总体变化不是很大，同时移动床的厚度呈现先略微增加，然后再逐渐减小的趋势，但是从整体而言整个岩屑床(固定床和移动床)的环空无因次岩屑床厚度是在逐渐减少的；当井斜角θ减小到60°左右时，移动岩屑床和固定岩屑床便会消失，取而代之的是由岩屑颗粒组成的滑移层，该层在下井壁上会存在多种形式的运动方式，从理论上来讲，它可以沿着井壁向上滑动、静止于井壁上或者沿着井壁向下滑移，这都取决于它的受力状态。随着井斜角θ的进一步降低，该层上表面的岩屑颗粒会受到泡沫钻井液的拖拽力和上举力的作用进入到悬浮层中，进而导致该层的横截面积会随着θ的减小而减小；当井斜角降低到30°以下时，由于井斜角较小，岩屑基本不会沉积在井壁上形成岩屑床，因此此时的岩屑都悬浮在泡沫流体中，只要环空泡沫返速大于岩屑的沉降速度，岩屑就会被稳定泡沫带出井口。

从图4中可知，该井水平段的无因次岩屑床厚度平均约为33%，超过了一般允许环空井眼下部存在的岩屑床厚度的10%[15]，远超过了安全值。因此，可以判断该井井眼净化效果不良。

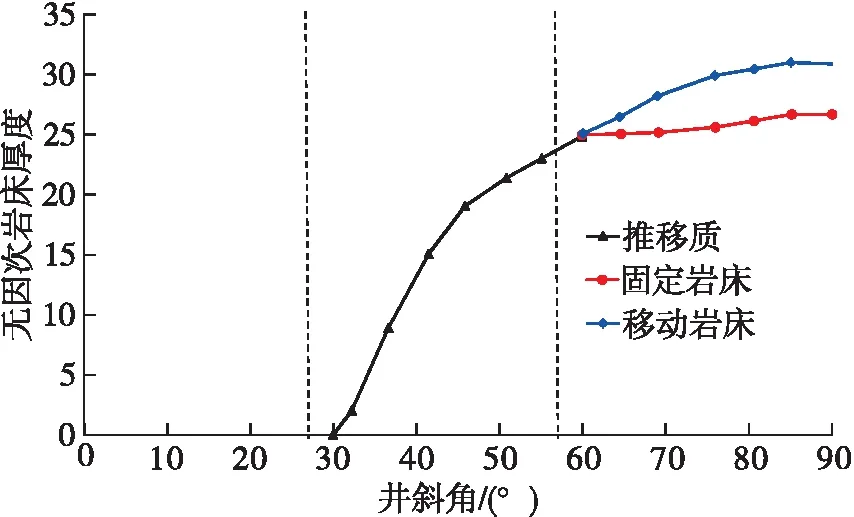
图4 无因次岩屑床厚度随井斜角变化的分布曲线

图5为不同环空泡沫返速下的无因次岩屑床厚度随井斜角变化的分布规律。从图5中可以看出，随着环空返速的增大，环空中的无因次岩屑床厚度逐渐减少。无因次岩屑床厚度在井斜角在30°～60°的范围内时，整个岩屑床的厚度都是随着井斜角的增大而增加，而在60°～90°的范围内岩屑床厚度则逐渐减小，但岩屑床的厚度依旧大于10%，这一规律同泡沫钻井中斜井段的环空携岩难度较大的实际是相吻合的。

图5 不同环空泡沫返速下的无因次岩屑床厚度随井斜角变化的分布曲线

图6为泡沫质量—深度关系曲线，从图6中可以看出，在同一个深度上环空中的泡沫质量总是大于钻柱内的泡沫质量。随着井深的增加环空和钻柱内的压力的增加，导致泡沫流体中的气相体积减小，使得泡沫质量降低。

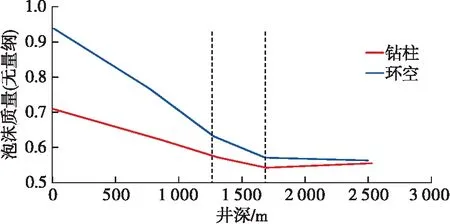
图6 泡沫质量—深度关系曲线

图7是稳定泡沫的泡沫质量同无因次岩屑床厚度之间的关系曲线，从图7可知，随着泡沫质量的增大，环空中岩屑床的厚度也随之降低，当环空速度恒定并且比泡沫质量较低的泡沫钻井液更早达到稳定状态时，增加的泡沫质量降低了环空钻屑的浓度，泡沫的携岩效果好。

图7 泡沫质量与无因次岩屑床厚度的关系曲线

图8为岩屑粒径对岩屑床厚度的影响关系，从图8中可以看出，岩屑颗粒越小，越有利于稳定泡沫对岩屑的携带作用。当岩屑直径小于2 mm时，岩屑床厚度逐渐趋于稳定，此时再减小岩屑的粒径对泡沫携岩效果不大。因此，在泡沫质量一定的情况下，应该尽量选择粒径较小的颗粒。

图8 岩屑粒径与无因次岩屑床厚度的关系曲线

图9为偏心度e对轴向速度分布的影响(x轴正方向为井眼底侧，负方向为井眼上侧)，从图9中可知，偏心度e越大，环空宽间隙处的流速就越大，而窄间隙处的流速就越小，同时宽窄间隙的流速差也会相应的增加。

图9 偏心度e对轴向速度分布的影响

图10为井斜角为90°时，钻杆偏心度与无因次岩屑床厚度之间的关系。

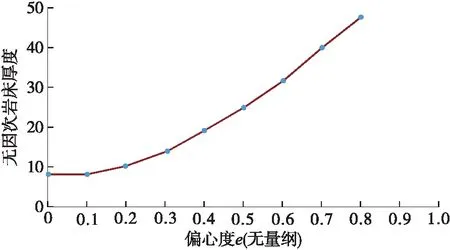
图10 偏心度e与无因次岩屑床厚度的关系曲线

由图10可知，随着钻杆偏心度的逐渐增大，环空中的岩屑床厚度也随之增大；同时，从曲线上各点的斜率也可以看出，在偏心度比较大时，偏心度的变化对岩屑床厚度的影响比较大，而在偏心度较小时，其对岩屑床厚度的影响也相对较小，尤其是从偏心度减少到0.2之后，随着偏心度的继续减小,环空岩屑床的厚度几乎不再改变，这是由于随着偏心度的减小，钻柱将不在同处于环空下部的岩屑床相接触,同时,偏心度对流场的影响效果也将降低，此时,如果继续降低偏心度，则对岩屑床厚度的大小影响不大。

3 结论

(1)稳定泡沫对环空的清洁作用比钻井液更好，环空中岩屑床的厚度随着井斜角的减小而减小，同时环空中岩屑颗粒越细小，越有利于泡沫对其的携带。

(2)在钻柱偏心度较大的大斜度井段，依然会存在井眼清洁效果不良的情况。因此，利用钻柱旋转的机械刮削和搅动作用，破坏岩屑床，也可以适当增加泡沫流速，通过紊流扰动辅助清除岩屑床，以便更好地改善大斜度井眼的清岩效果。

(3)现场作业过程中，可通过提高泡沫流速或增加泡沫质量来减小岩屑床的厚度，泡沫流速对清岩效果的提升作用在一定范围内比较明显；同时也可以通过调节钻柱转速来改变周向流场分布，进一步提升泡沫的携岩能力。